
Algoritmos de Recomendação
Felipe Cruz
@felipejcruz
github.com/felipecruz

Problema
Algoritmos
CF & RBMs
Motivação?
relevância
eficiência
personalização
?
Problema
?
?
?
?
?
?
?
?


+
=
?
Quantos usuários?
Quantos produtos?
Recomendação não serve apenas para "Big Data", só que..
quanto maior for a matriz, mais recursos são necessários
Problema
AlgoritmosCF & RBMs
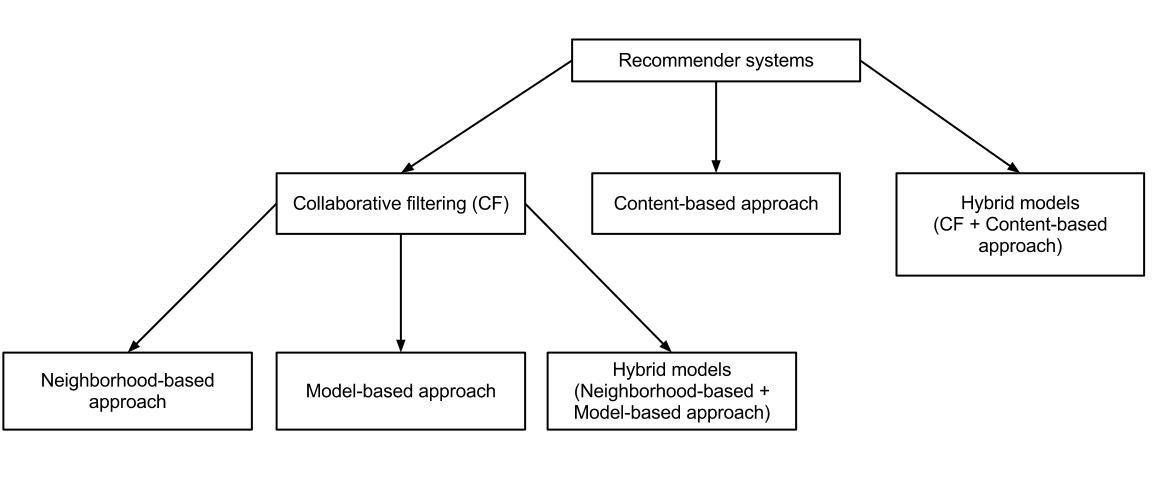
Sistemas de Recomendação

Sistemas de Recomendação
Filtragem Colaborativa
Similaridade
(neighborhood based)
Procedimento de treino
Para cada usuário

Descobre usuários que compraram produtos em comum



Procedimento de treino
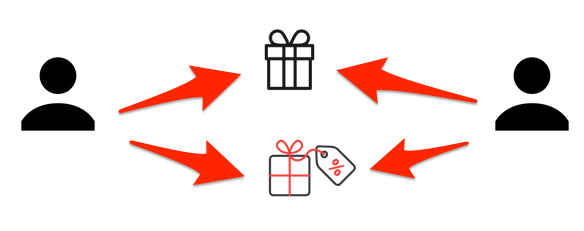
Procedimento de treino
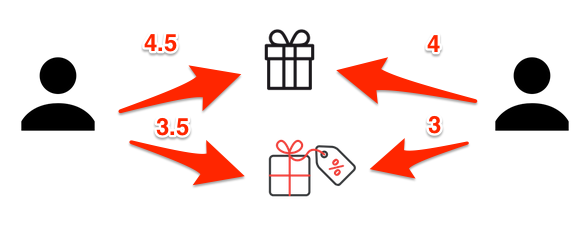
agora podemos calcular a similaridade

f(
)
f
é a função de similaridade
f(a, u, I) = \frac{\sum_{i \in I} (r_{a,i} - \overline{r_a}) (r_{u,i} - \overline{r_u})}{\sqrt{\sum_{i \in I} (r_{a,i} - \overline{r_a})^{2} \sum_{i \in I}(r_{u,i} - \overline{r_u})^{2}}}
Pearson correlation
nota dada pelo usuário a ao item i menos média das notas do usuário a
I = \{ \quad , \quad \}


\sum_{i \in I} (r_{a,i} - \overline{r_a})
(r_{u,i} - \overline{r_u})
\sum_{i \in I} (r_{a,i} - \overline{r_a})
(r_{u,i} - \overline{r_u})
[(4.5 - 4)(4 - 3.5)] + [(3.5 - 4)(3 - 3.5)]


[0.5 \times 0.5]+[-0.5 \times -0.5] = 0.5
\sqrt{\sum_{i \in I} (r_{a,i} - \overline{r_a})^2 \sum_{i \in I} (r_{u,i} - \overline{r_u})^2}
[(4.5 - 4)^2 + (3.5 - 4)^2] \times [(4 - 3.5)^2 + (3 - 3.5)^2]




[(0.5)^2 + (-0.5)^2] \times [(0.5)^2 + (-0.5)^2] = \sqrt{0.5^2} = 0.5
\frac{0.5}{0.5} = 1
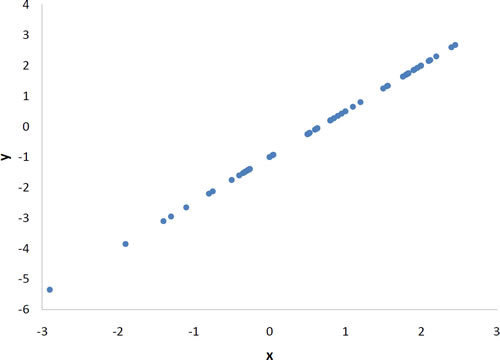
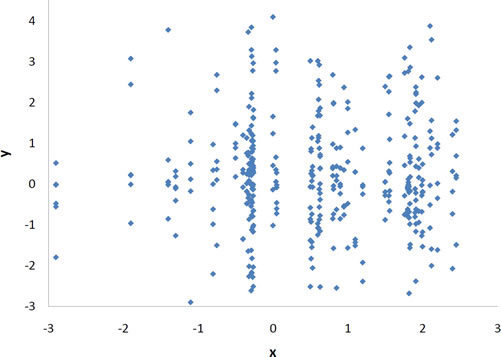
Predição?
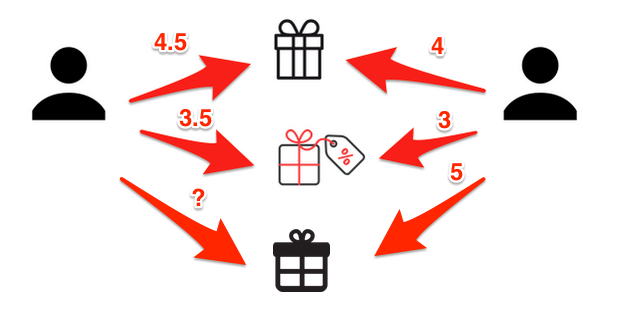
p_{a,i} = \overline{r_{a}} + \frac{\sum_{u \in K}(r_{u,i} - \overline{r_{u}}) \times w_{a,u}}{\sum_{u \in K} w_{a,u}}
Predição
p_{a,i} = 4 + \frac{5 - 3.5 \times 1}{1} = 5.5
Predição
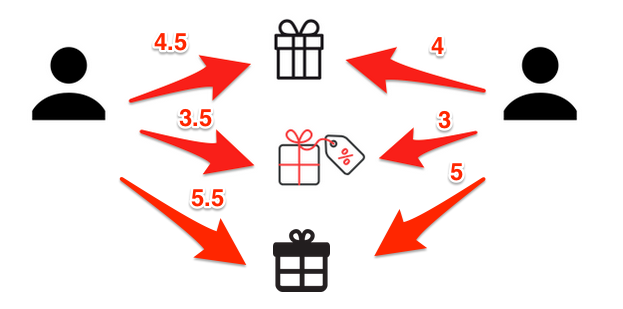
Template method - treino
- for u in usuarios:
- similares = mesmos_produtos(R, u)
- for s in similares:
- S[(u,s)] = similaridade(u, s)
Outras medidas de similaridade
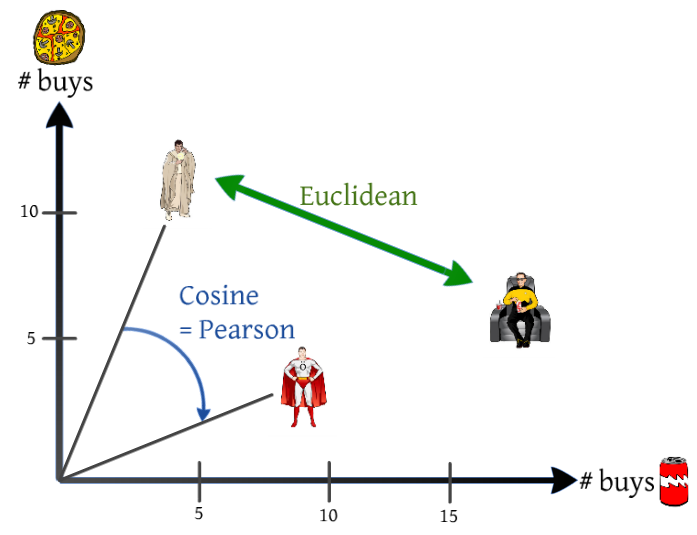
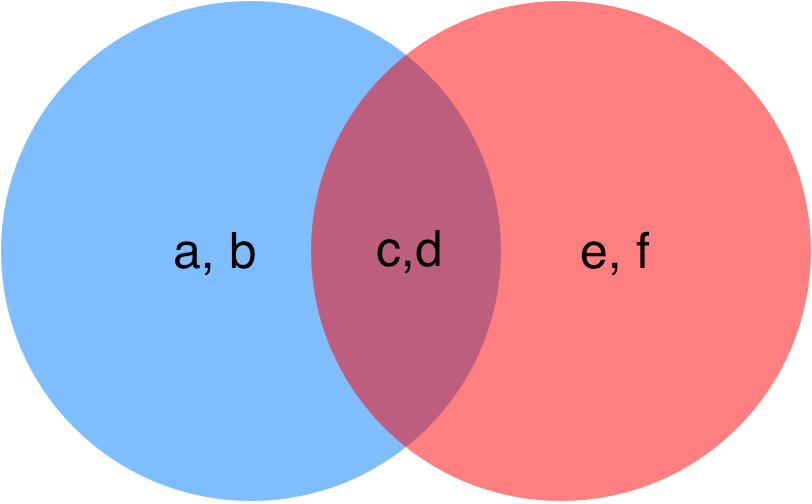
Jaccard
pausa...
Fator latente

(model based)
Capturar informação implícita
Capturar informação implícita
#comofaz
?
?
?
?
?
?
?
?
R_{ij} \in

(u \times p)
Vamos dar um nome aquela matriz:
Model Based?
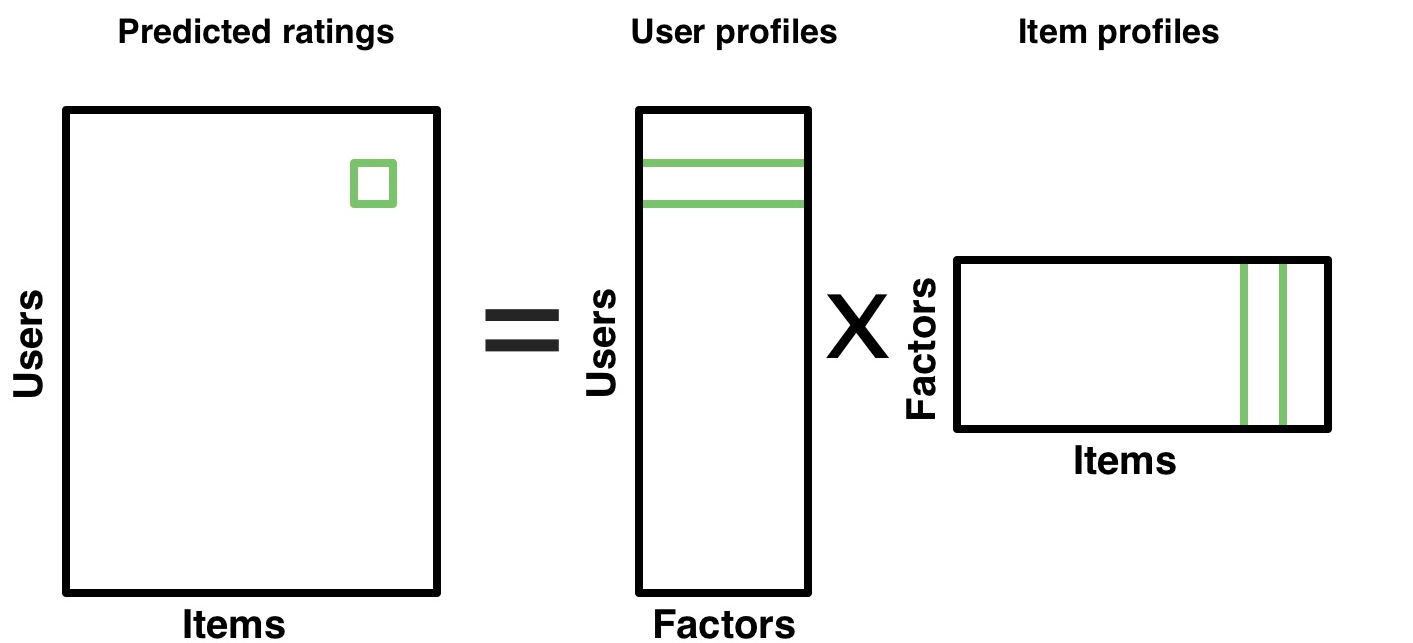
Modelo
\langle u_{i},p_{j} \rangle \approx R_{ij}

Fatorar matrizes
\overline{R}_{(u \times p)} = U_{(u \times k)}P_{(k \times p)}
\text{min} \sum_{i,j \in L}(r_{i,j} - u_{i}p_{j})^2
U,P
T
+ \lambda \left(\sum_{i} n_{u_i} \left \vert\vert u_i \right \vert\vert ^2 + \sum_{j} n_{v_j} \vert\vert v_j \vert\vert^2 \right)
Formalização do Problema
\langle u_{i},p_{j} \rangle
\text{min} \sum_{i,j \in L}(r_{i,j} - u_{i}p_{j})^2
U,P
T
+ \lambda \left(\sum_{i} n_{u_i} \left \vert\vert u_i \right \vert\vert^2 + \sum_{j} n_{v_j} \vert\vert v_j \vert\vert^2 \right)
Formalização do Problema
Regularização contra overfit
\text{min} \sum_{i,j \in L}(r_{i,j} - u_{i}p_{j})^2
U,P
T
E =
\left( \begin{array}{cc}
2 & 4 \\
3 & 6 \end{array} \right)
-
\left( \begin{array}{cc}
\langle u_{1},p_{1} \rangle & \langle u_{1},p_{2} \rangle \\
\langle u_{2},p_{1} \rangle & \langle u_{2},p_{2} \rangle \end{array} \right)
Minimizar o erro
R_{ij}
\overline{R}_{ij}
Algoritmo ALS
- Inicializa U com valores randômicos
- Fixa U, e para cada linha de P resolvemos um problema de regressão linear para achar valores ótimos para P
- Fixa P, e para cada linha de U resolvemos um problema de regressão linear para achar valores ótimos para U
ALS
Ajusta traseira
Ajusta frente
Ajusta traseira
Ajusta frente
Problema
AlgoritmosCF & RBMs
RBM
- Modelo generativo
- Reconhece e completa padrões
- Algoritmo de aprendizado eficiente
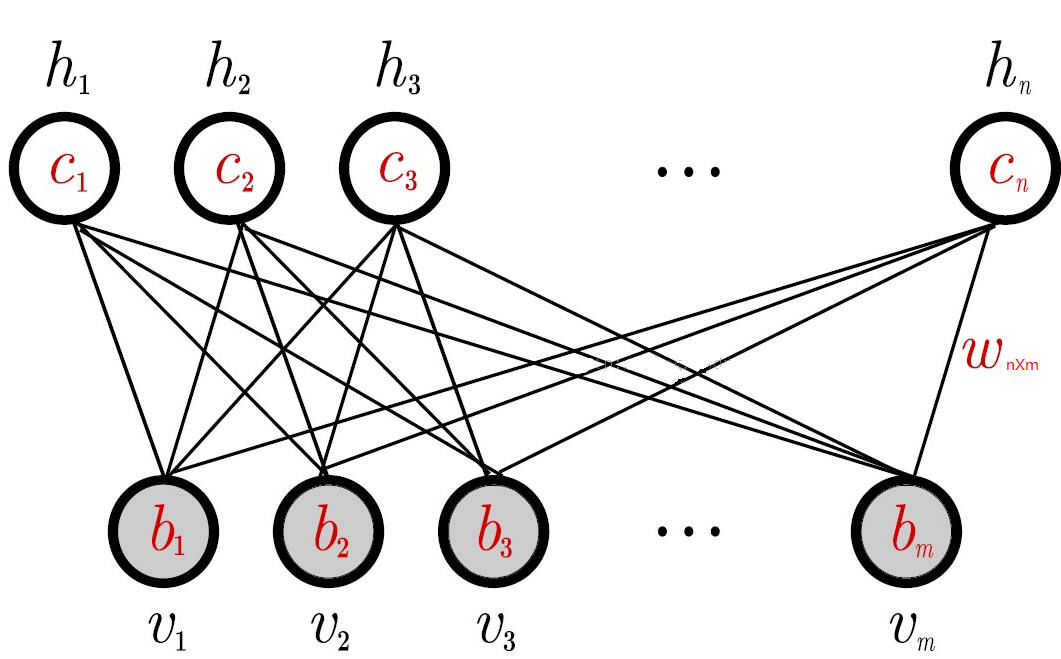




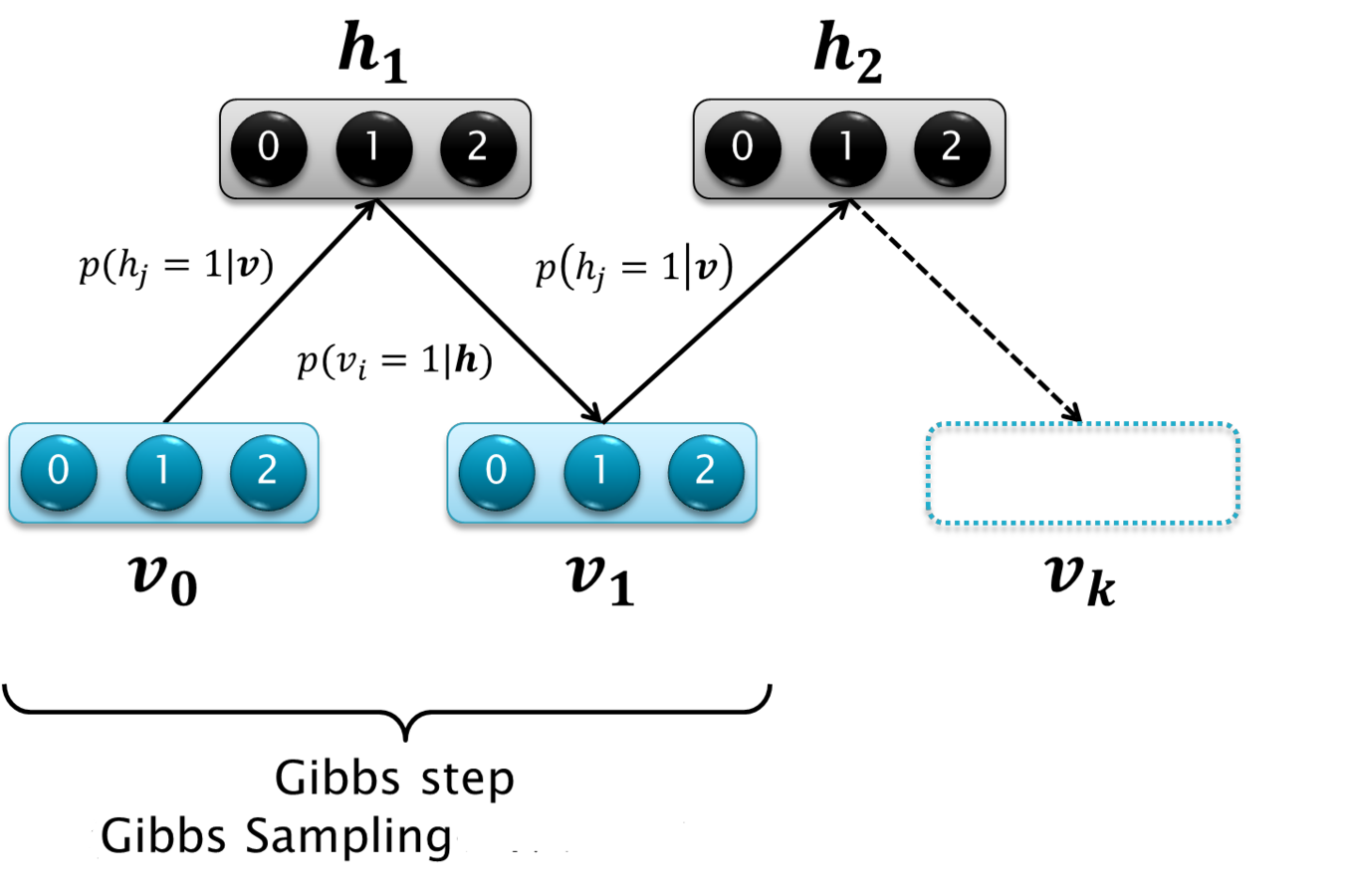






RBMs & CF
Modelo
- Cada destino é uma unidade visível
- 1 se comprou
- 0 se não comprou
Também é possível usar atributos do usuário no modelo. Ex: tem filhos? Só compra pacotes de luxo?
Predição - input
profile = [0, 0, 0, 1, 0, 0, 0, 1]
(buzios e ilha grande)
Predição - output
pred = [0, 1, 0, 1, 0, 0, 1, 1]
(buzios, ilha grande, angra, balneário camboriú)
RBM
ALS
Na prática
- Funciona* bem com amostras do dataset
- Perfis vazios voltam com destinos mais populares
- Predição não determinística
- Pode ser usada antes de um modelo de Rating pra diminuir a quantidade de predições necessárias
- Ensemble!!!
http://www.slideshare.net/akyrola/largescale-recommendation-systems-on-just-a-pc
Perguntas?
@felipejcruz
github.com/felipecruz
Recomendação e Algoritmos de Filtragem Colaborativa
By Felipe Cruz
Recomendação e Algoritmos de Filtragem Colaborativa
- 1,183



