How to cook a universe?


PHENIICS FEST, 2025/07/03
Hugo SIMON,
PhD student supervised by
Arnaud DE MATTIA and François LANUSSE


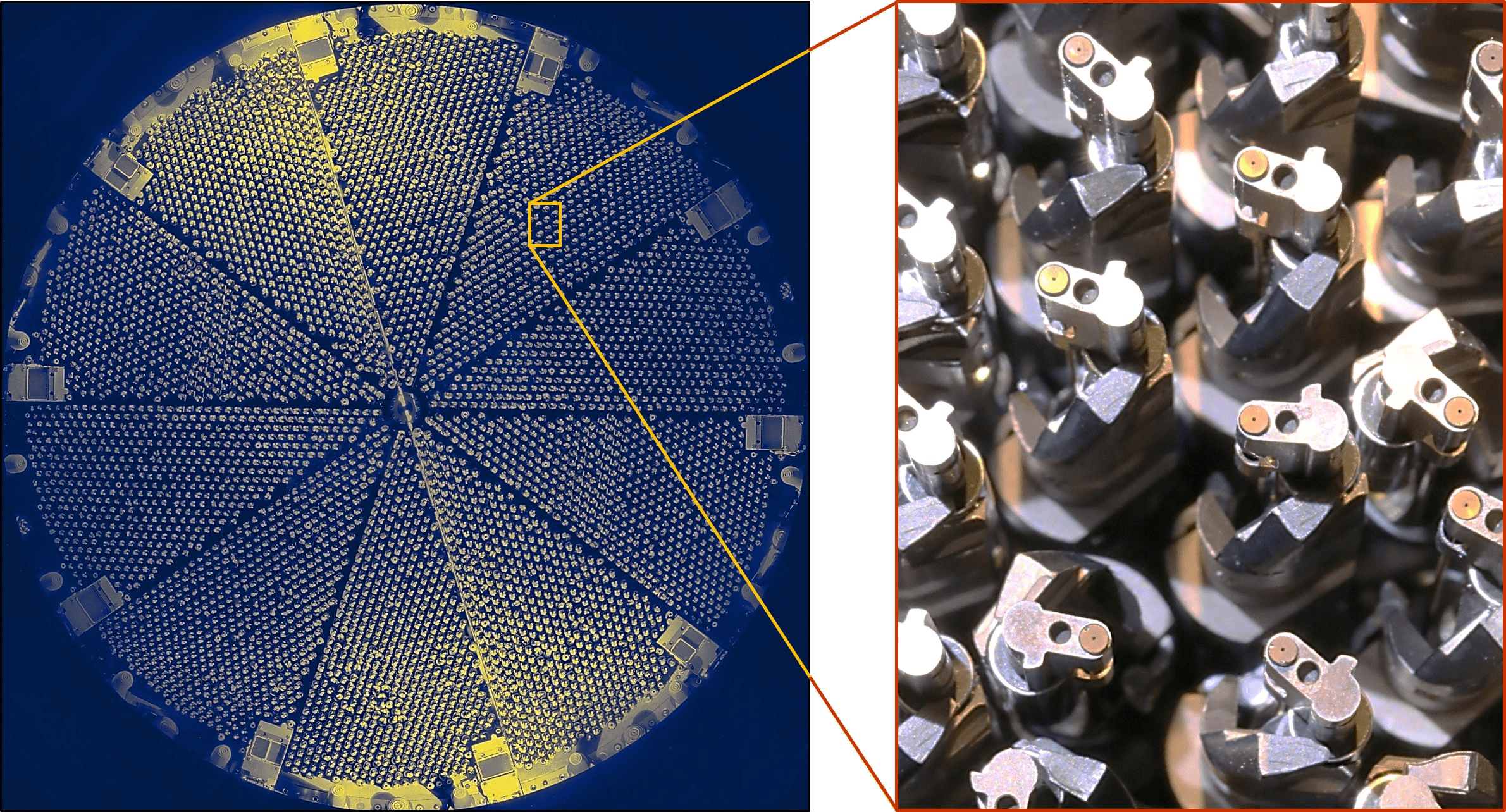

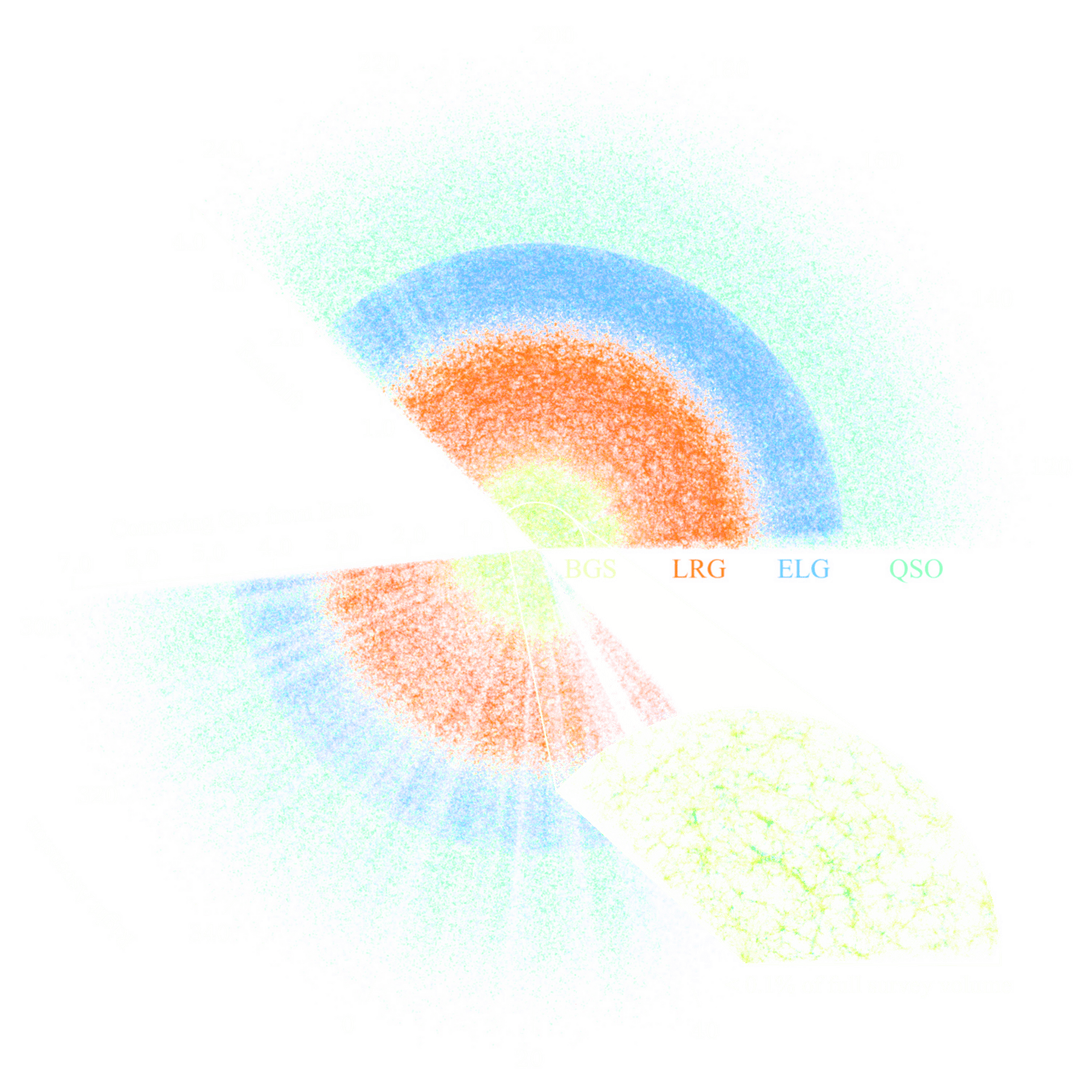
\(\approx 40 \textrm{ million galaxies} \)
Observations:
- Universe seems everywhere similar
- Matter follows a particular filamentary distribution
galactic plane

Observations:
- Universe seems similar everywhere
- Matter follows a filamentary distribution
galactic plane


Which recipe for the Universe?
"A female kitchen chef amazed while discovering a cake made out of the universe with its large scale structures of galaxies."

Consequence:
- content determines how space-time curves
- space-time curvature determines how content moves
Consequence:
- Universe does not revolve around humankind
- Universe is similar, wherever you look from, whatever the direction
Copernicus, XVI CE
Einstein, XX CE
We are no privileged observers

$$G_{\mu\nu}= \kappa T_{\mu\nu}$$

Consequence:
- Evolution of the Universe is determined by its content
Consequence:
- Universe is statistically
homogeneous and isotropic
A starter to a recipe...

Copernicus, XVI CE
Einstein, XX CE
We are no privileged observers

$$G_{\mu\nu}= \kappa T_{\mu\nu}$$

Consequence:
- Evolution of the Universe is determined by its content
A starter to a recipe...
Consequence:
- Universe is statistically
homogeneous and isotropic
...remains to find the ingredients!

+

light
ordinary matter


dark matter
dark energy



❌
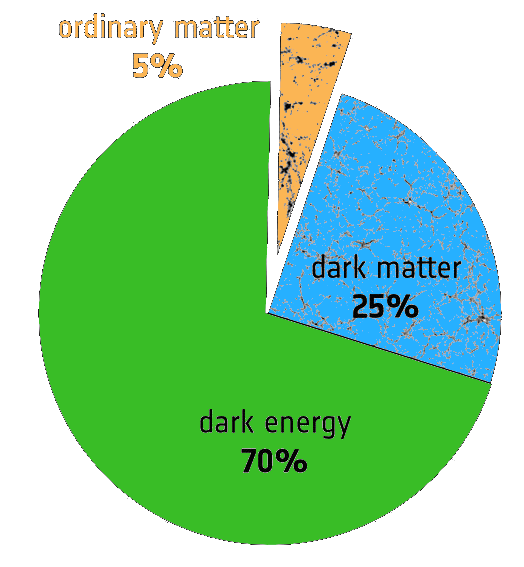
Current estimation
...but in what proportions?
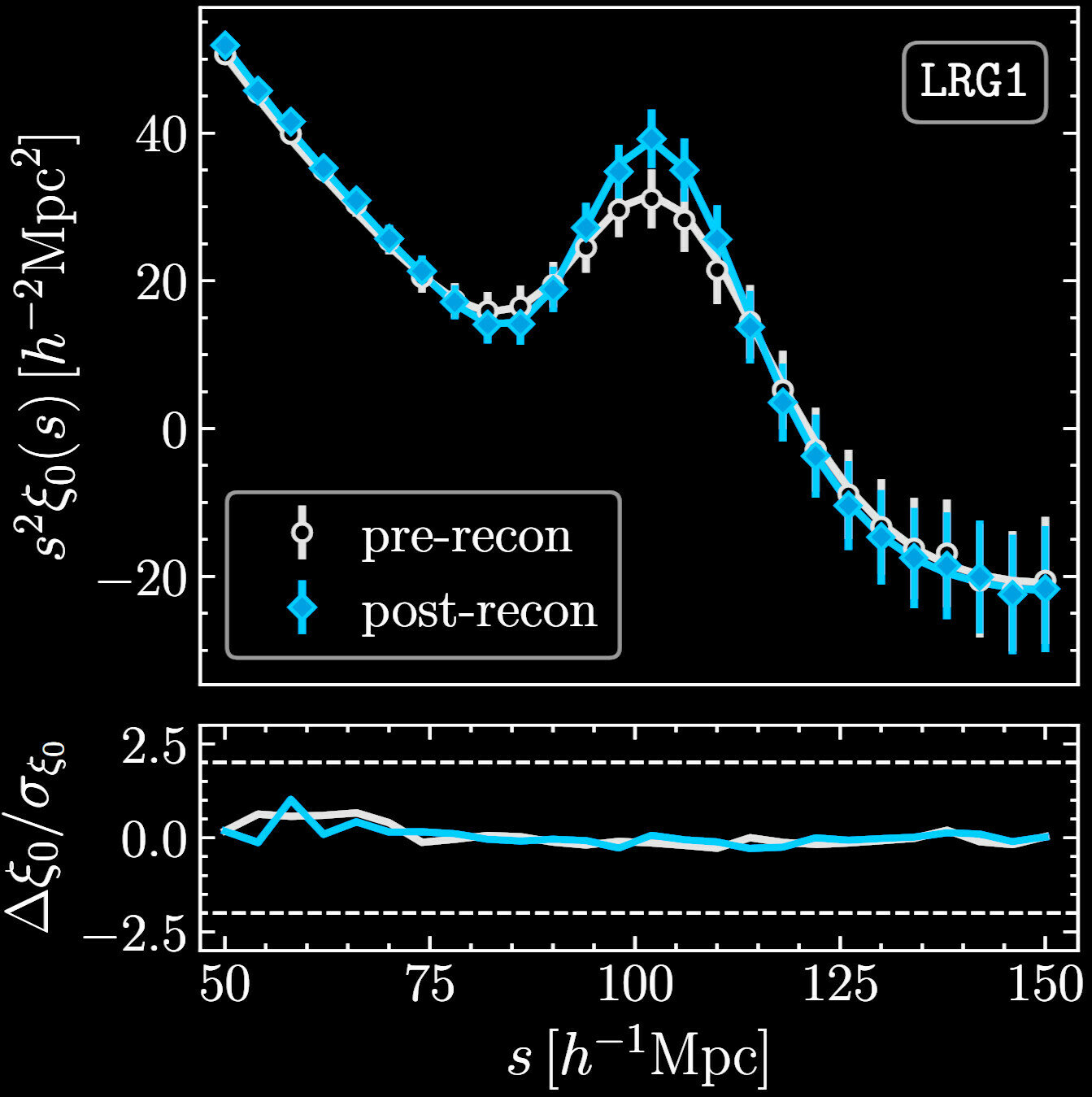
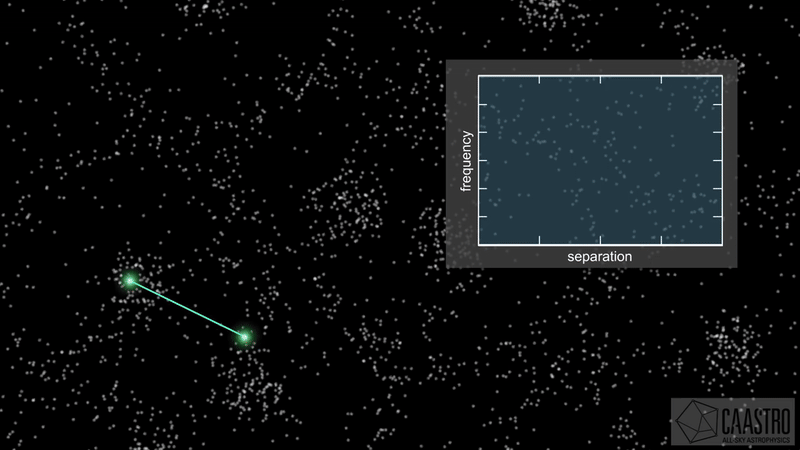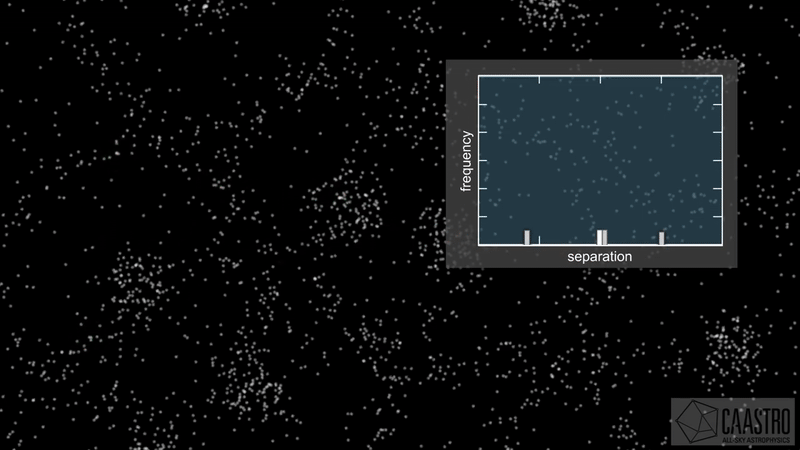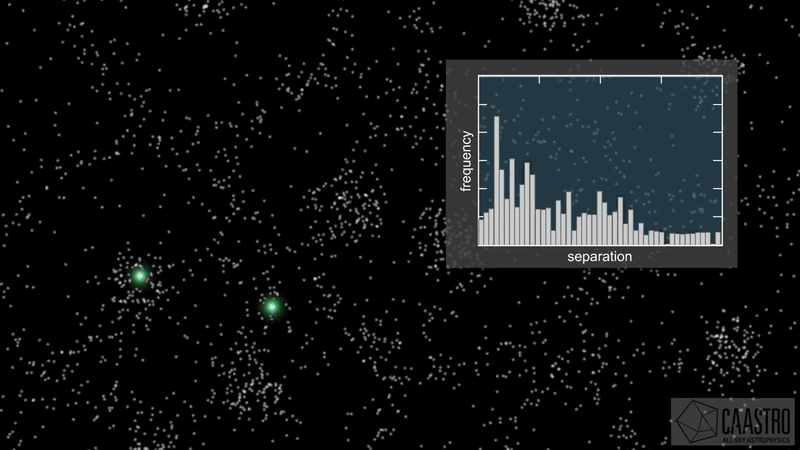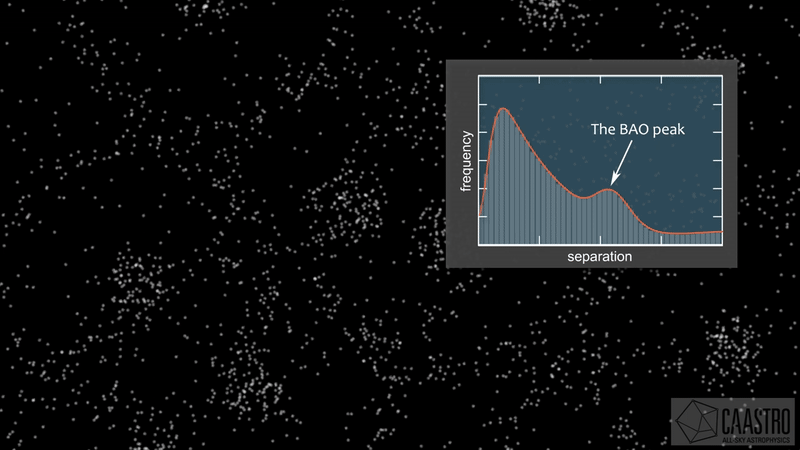
- Whole Universe map \(\delta_\mathrm{g}\) is compressed into a 2PCF/power spectrum \(P\)
- Then Bayesian inference obtains \(\mathrm{p}(\Omega \mid P)\)
Compressing the Universe

\(\Omega\)
\(\delta_\mathrm{i}\)
\(\delta_\mathrm{g}\)
\(P\)
Non-linear physics at play
- At large scales, Gaussian field so power spectrum is lossless compression
- At small scales however, matter field is non-Gaussian
Gaussianity and beyond
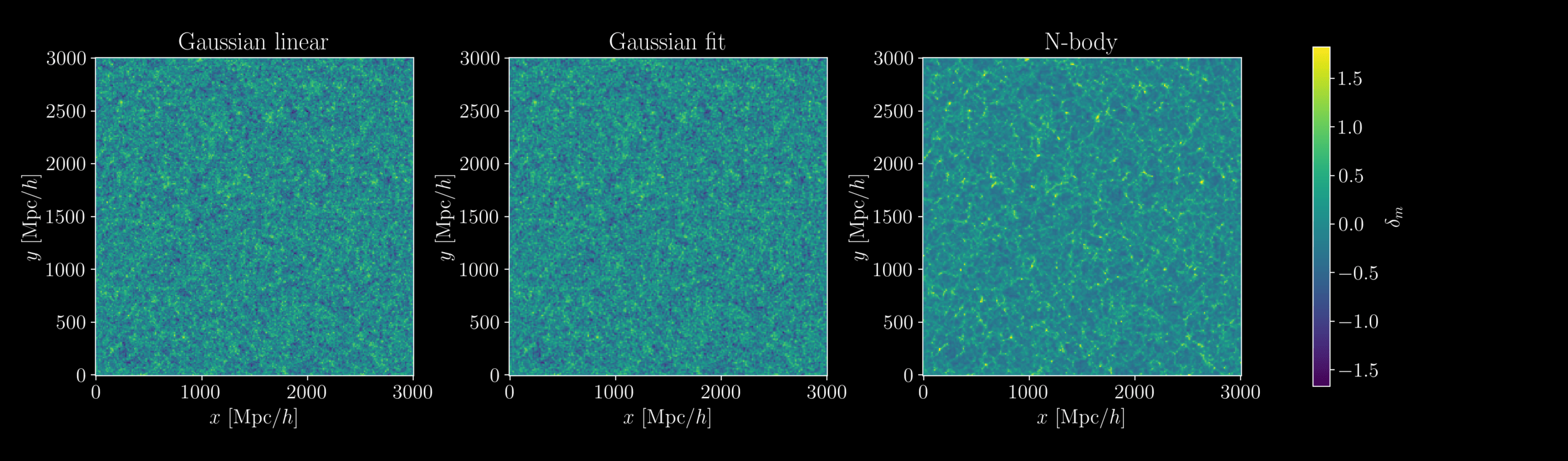
2 fields, 1 power spectrum: Gaussian or N-body?
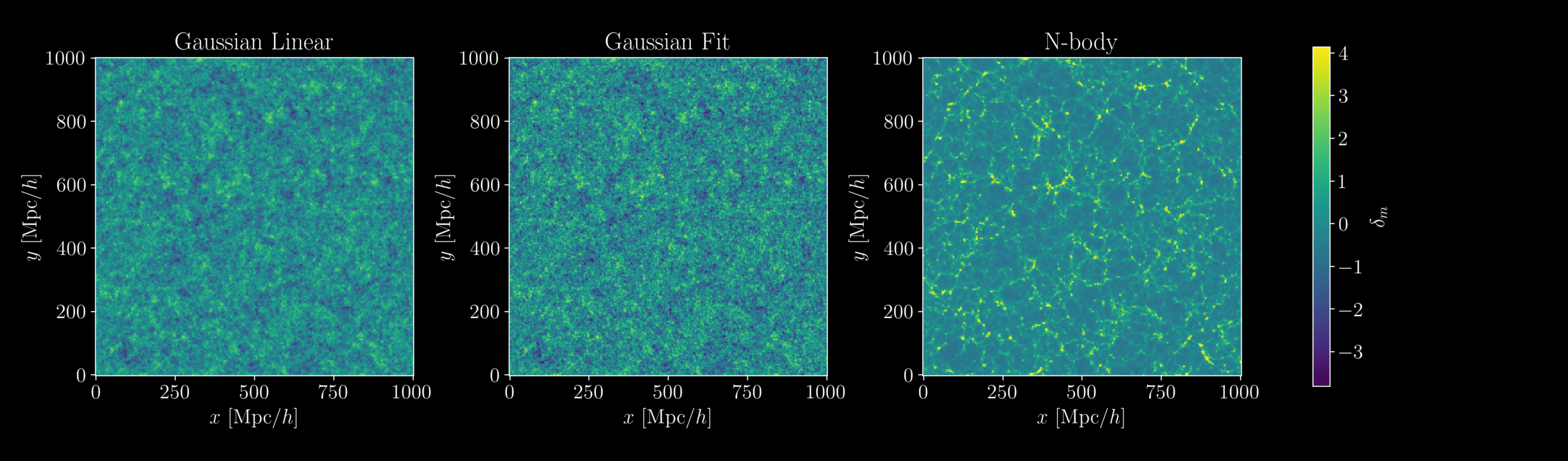
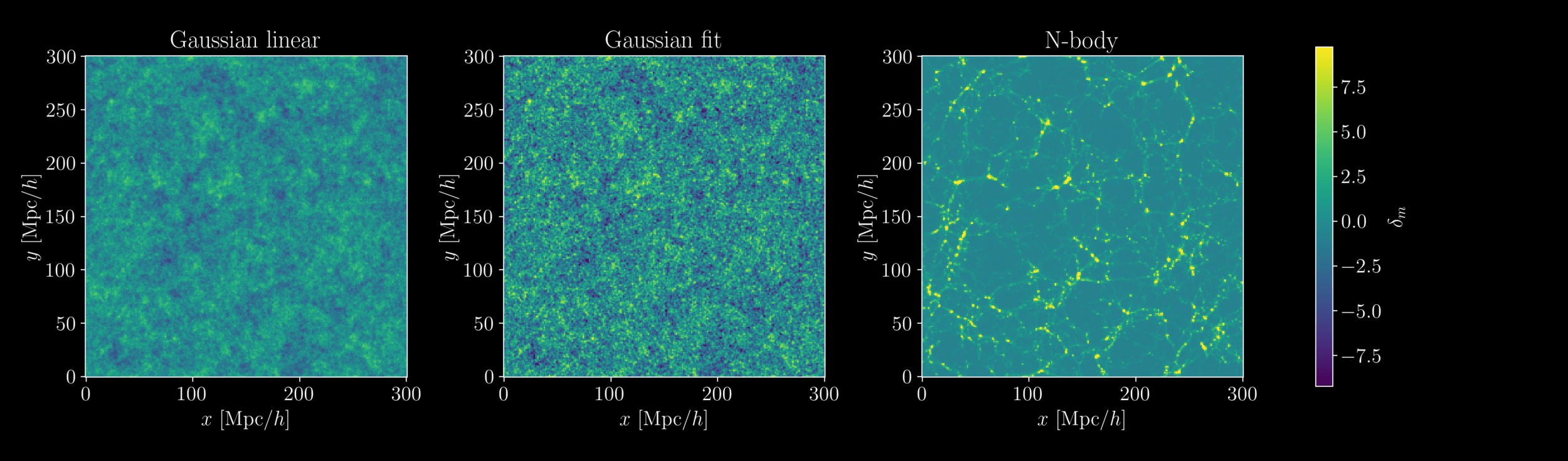
Simulating the Universe again and again
Bayesian inference at the field-level:
- Among all possible universes \(\Omega,\delta_\mathrm{i}, \delta_\mathrm{g}\), restrict to the ones compatible with observation \(\delta_\mathrm{g}^\mathrm{obs}\)
- This obtains \(\mathrm{p}(\Omega, \delta_\mathrm{i} \mid \delta_\mathrm{g})\)

\(\Omega\)
\(\delta_\mathrm{i}\)
\(\delta_\mathrm{g}\)

compare
repeat

\(\delta_\mathrm{g}^\mathrm{obs}\)
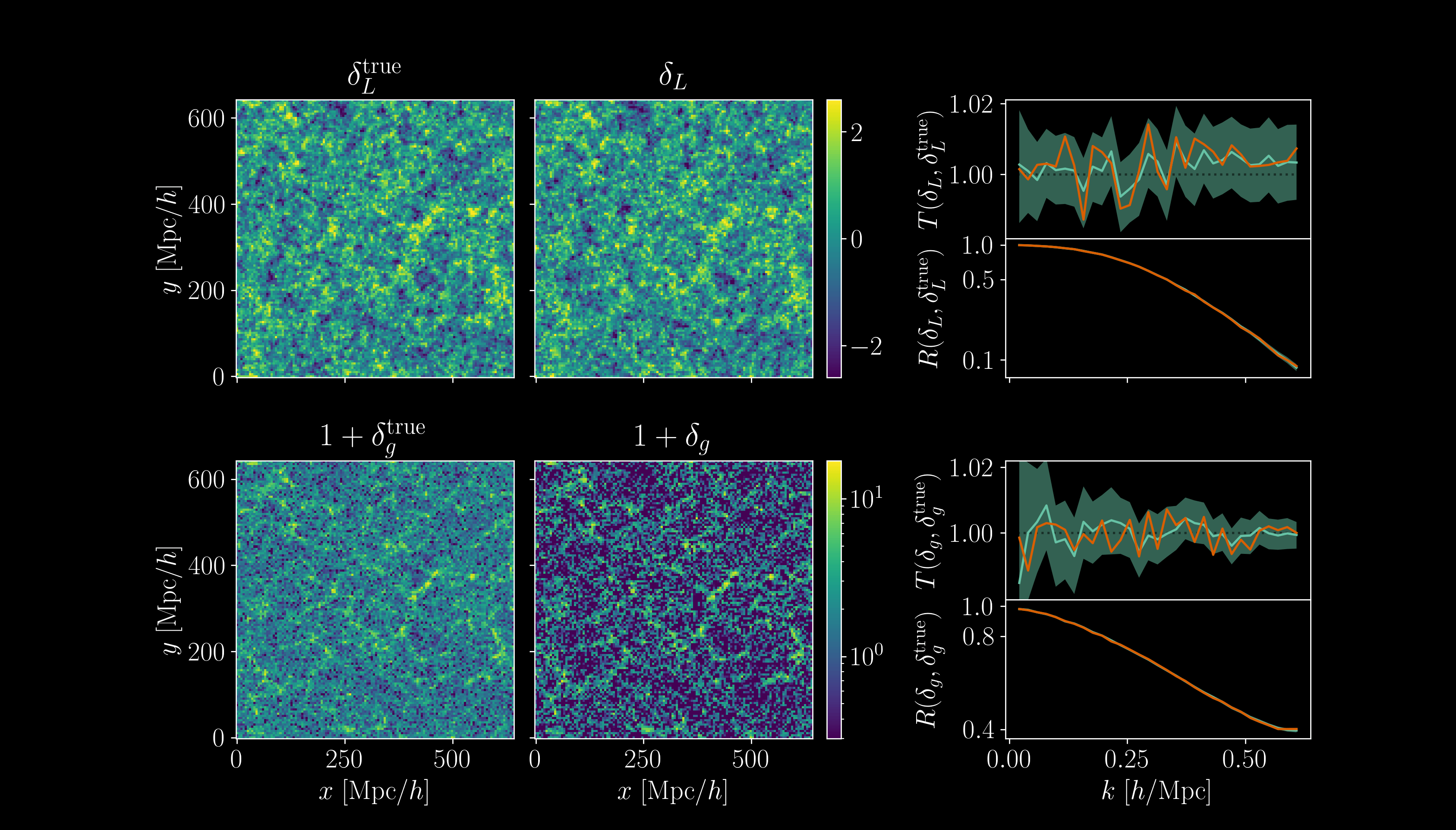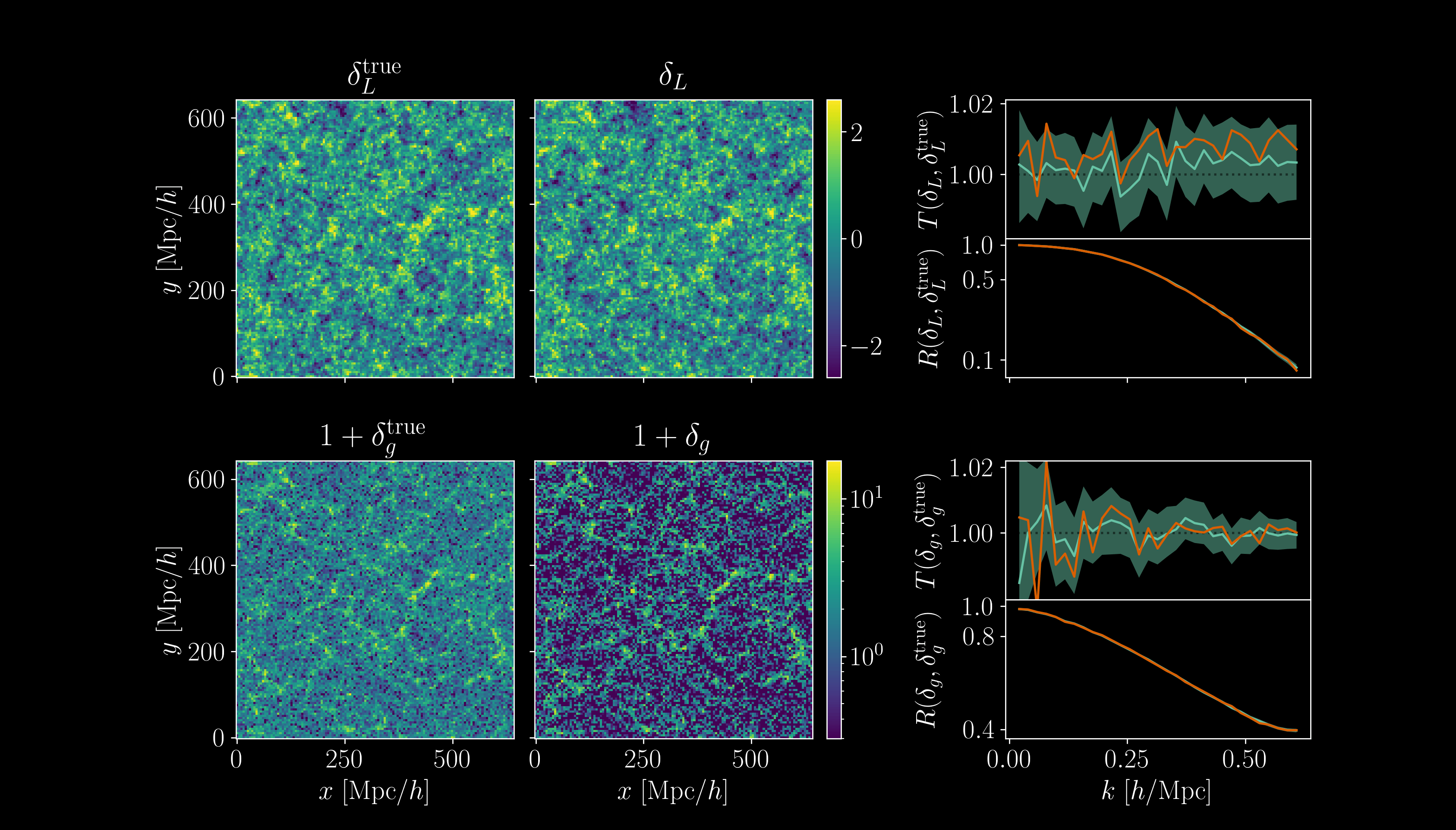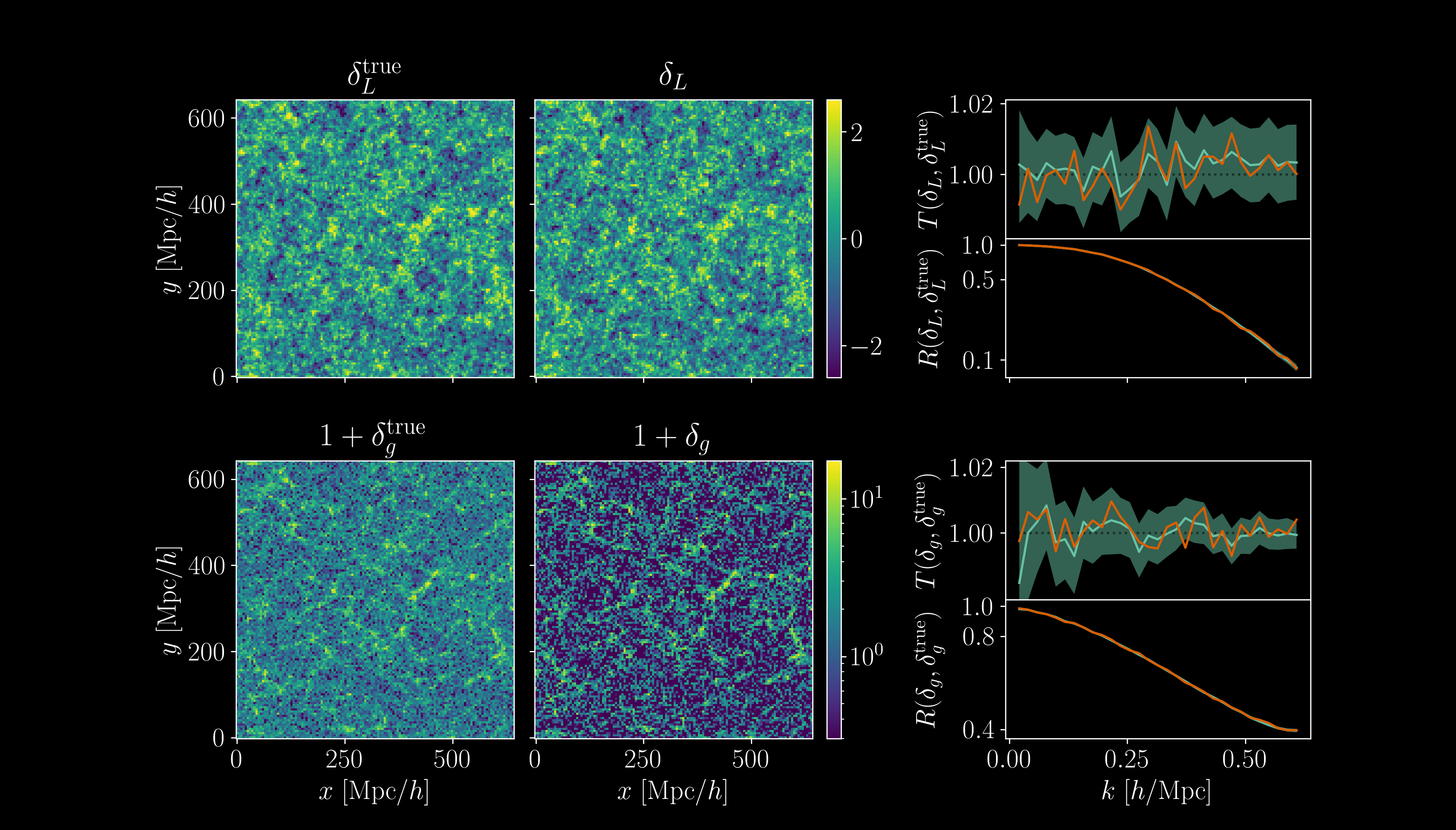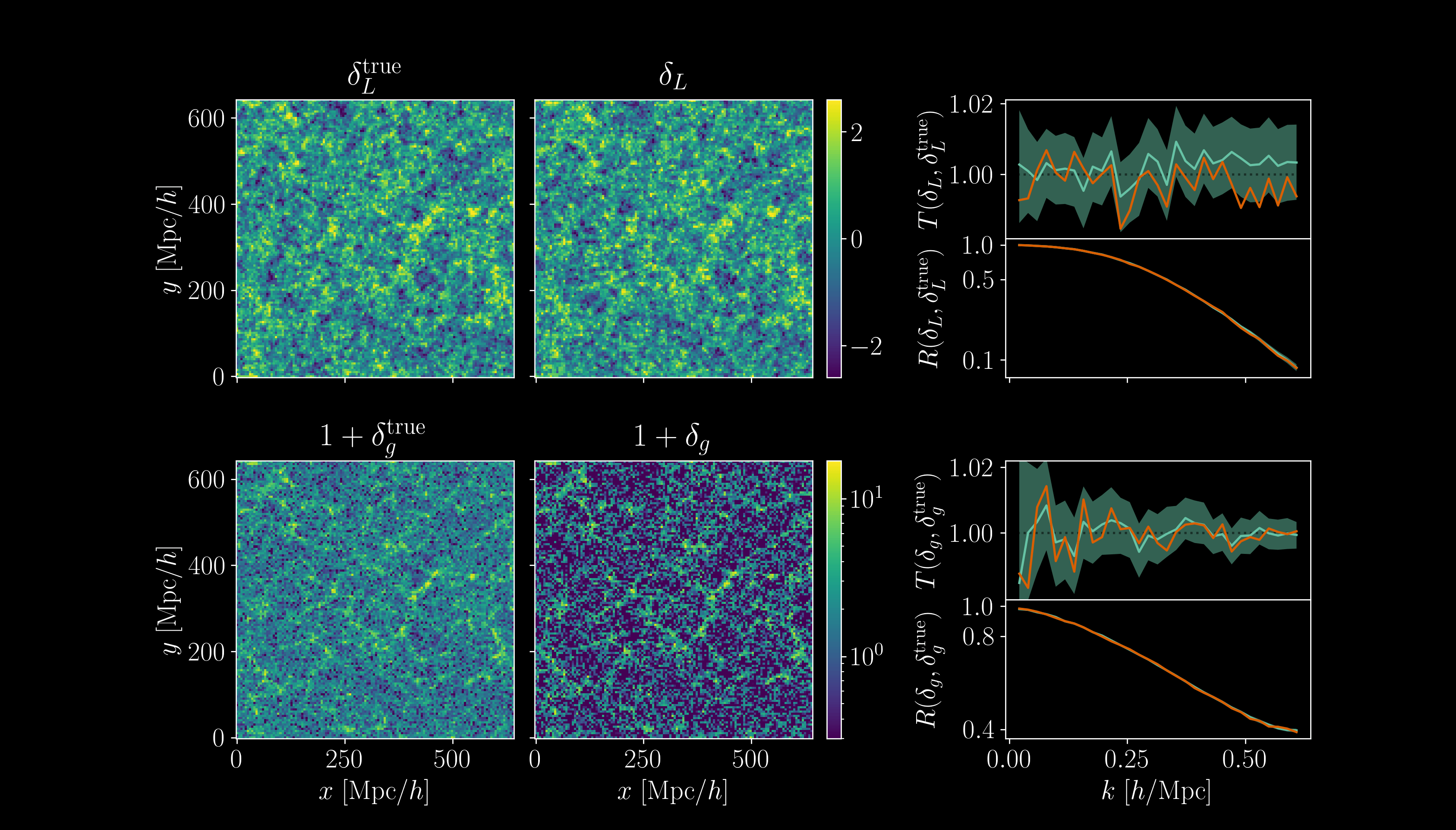
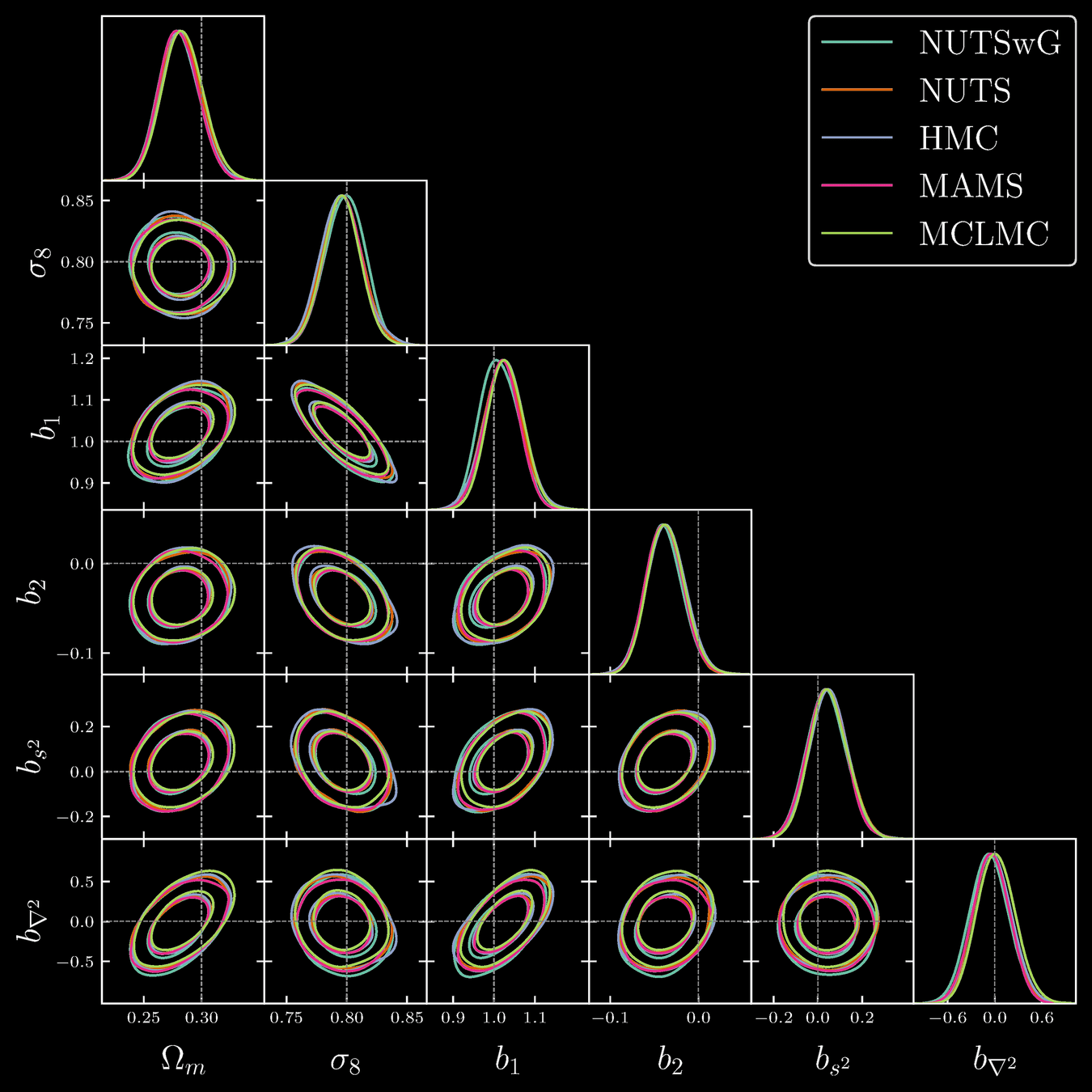
- High-dimensional sampling \((d \geq 10^7)\) using gradient-based MCMC
- 4h GPU MicroCanonical Langevin Monte Carlo (MCLMC)
vs. 80h GPU Hamiltonian Monte Carlo (HMC)
Field-level inference


Thank you!
2025FEST
By hsimonfroy
2025FEST
- 137