Integrable
When is the whole the sum of its parts?
2025 James B. Wilson

https://slides.com/jameswilson-3/integrable/
When it the whole the sum of its parts?

-
Goal: count all the words in all the files on the University's website.
-
Breaks up as codata
-
Individual pages, with links to others
-
Words, followed by other words.
-
-
If we can count words as 1, then to count all the words is to add up "integrate" all the parts.
Integral
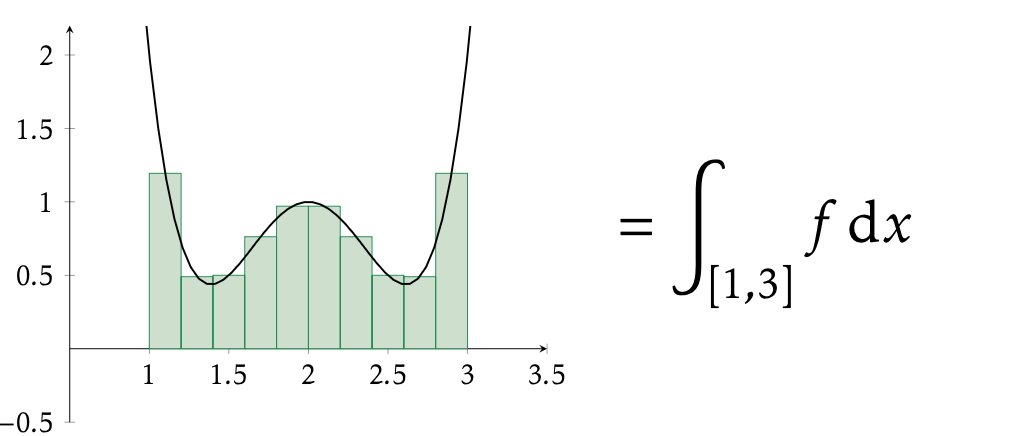
\(dx\)
\(f\)
Limit of sums
Domain
Codata is Integrable when...
-
There is a numerical measurement \(m\) that applies to the codata.
-
For each co-operator \[\begin{aligned} A & \rightarrow \bigsqcup_{\omega} A^{|\omega|}\\ a&\mapsto \text{case }h \quad (a_i)_{I\in I}, a_{|\omega|}]\end{aligned}\] we find \[m(a)=m(h)+\int_I a_i dm\]
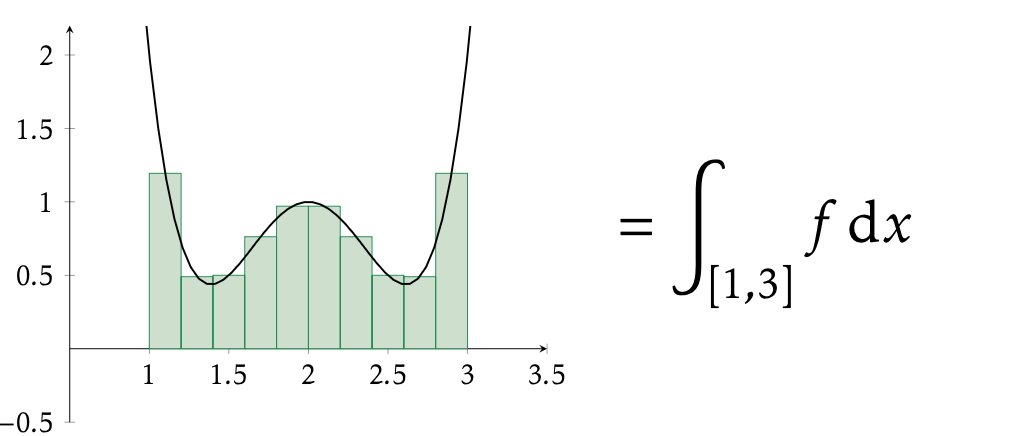
Choose an integrable domain:

-
Pick some form of codata
-
Identify its co-operators
-
Devise something to measure for about the parts of your codata.
-
Make sure you measure something integrable: the whole values should be the sum of its parts.




Measuring codata
\(\mathbb{A}\to \mathbb{A}\) "meters to meter+meters", "seconds to second+seconds"
1
2
3
Measuring codata
\(\mathbb{A}\to \mathbb{A}\) "meters to meter+meters", "seconds to second+seconds"
Unfold \(\mathbb{A}\to \mathbb{A}\)
\[as->(a_x,a_y)+as\]
If the data for keeps unfolding
\[(a_x,a_y)+(b_x,b_y)+(c_x,c_y)+...\]
which we might plot on a grid.
(1,0)
(0,1)
(1,1)
(2,2)
(2,0)
(2,1)
(0,2)
(1,2)
If the data unwraps as indexed in an area that the total data measure is growing proportional to what?
A function of the boundary.
Estimate growth type
-
Identify one co-operator
- Define a "center and radius" for how your data can expand from this co-operator.
- Estimate the total type of growth (length, area, volume, etc.)
Rates of Change
Measure: 2R, Perimeter: 2
Area: \((2R)^2\), Perimeter: \(4(2R)\)
Volume: \((2R)^3\), Surface Area: \(6(2R)^2\)
Rates of Change
Measure: 2R, Perimeter: 2
Area: \(\pi R^2\), Perimeter: \(2\pi R\)
Volume: \(\frac{4}{3}\pi R^3\), Surface Area: \(4\pi R^2\)

Predict Rate of change:

Given your integrable measurement, predict the rate of change of increasing the sample.




Your Codata's growth?
Measure: f(R), Perimeter: f(R)
\[\frac{d}{dR}\int_0^R perimeter(r) dr=measure(R)\]
Integrable systems
By James Wilson
Integrable systems
We will explore the idea of integrable systems.
- 147



