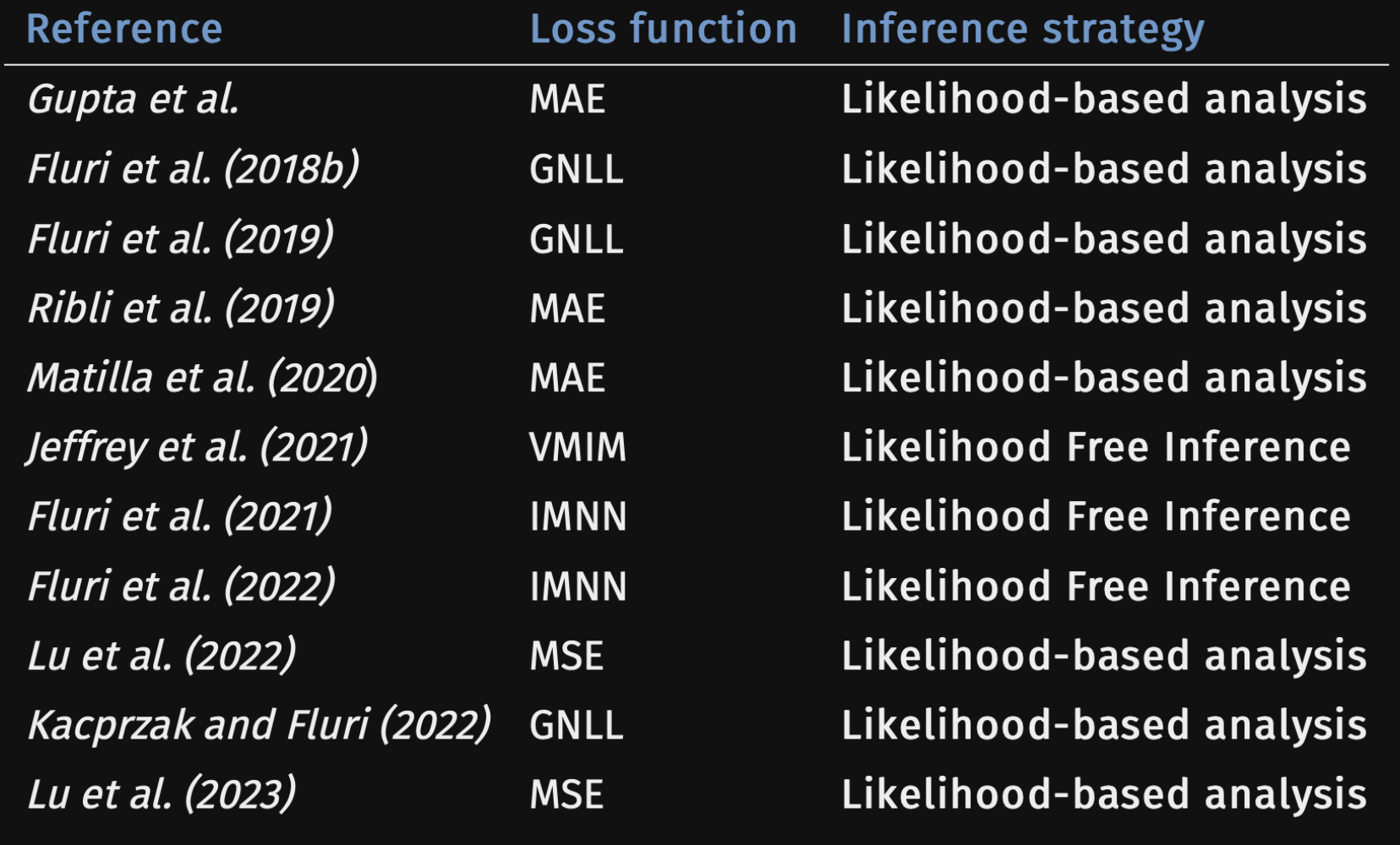
Simulation-Based Inference: estimating posterior distributions without analytic likelihoods
Rencontres Statistiques Lyonnaises, Villeurbanne, France
September 16, 2024
Justine Zeghal






credit: Villasenor et al. 2023
Quick cosmological introduction

Credit: ESATo date, the model that best describes our observations is
and it relies only on 6 cosmological parameters:
One big goal in cosmology is to determine the value of those parameters based on our observations.
Bayesian inference
Bayes theorem:
We want to infer the parameters that generated an observation
And run a MCMC to get the posterior
Bayesian inference
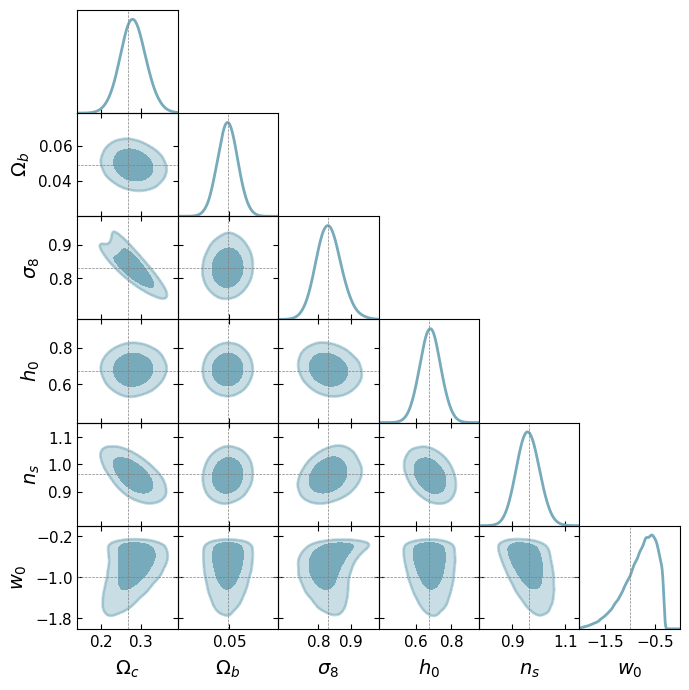
Cosmological context
Bayes theorem:
We want to infer the parameters that generated an observation
Bayes theorem:

Problem:
we do not have an analytic marginal likelihood that maps the cosmological parameters to what we observe
We want to infer the parameters that generated an observation
Credit: ESACosmological context
Bayes theorem:

Classical way of performing Bayesian Inference in Cosmology:
We want to infer the parameters that generated an observation
Credit: ESACosmological context
Bayes theorem:

We want to infer the parameters that generated an observation
Classical way of performing Bayesian Inference in Cosmology:
Power Spectrum
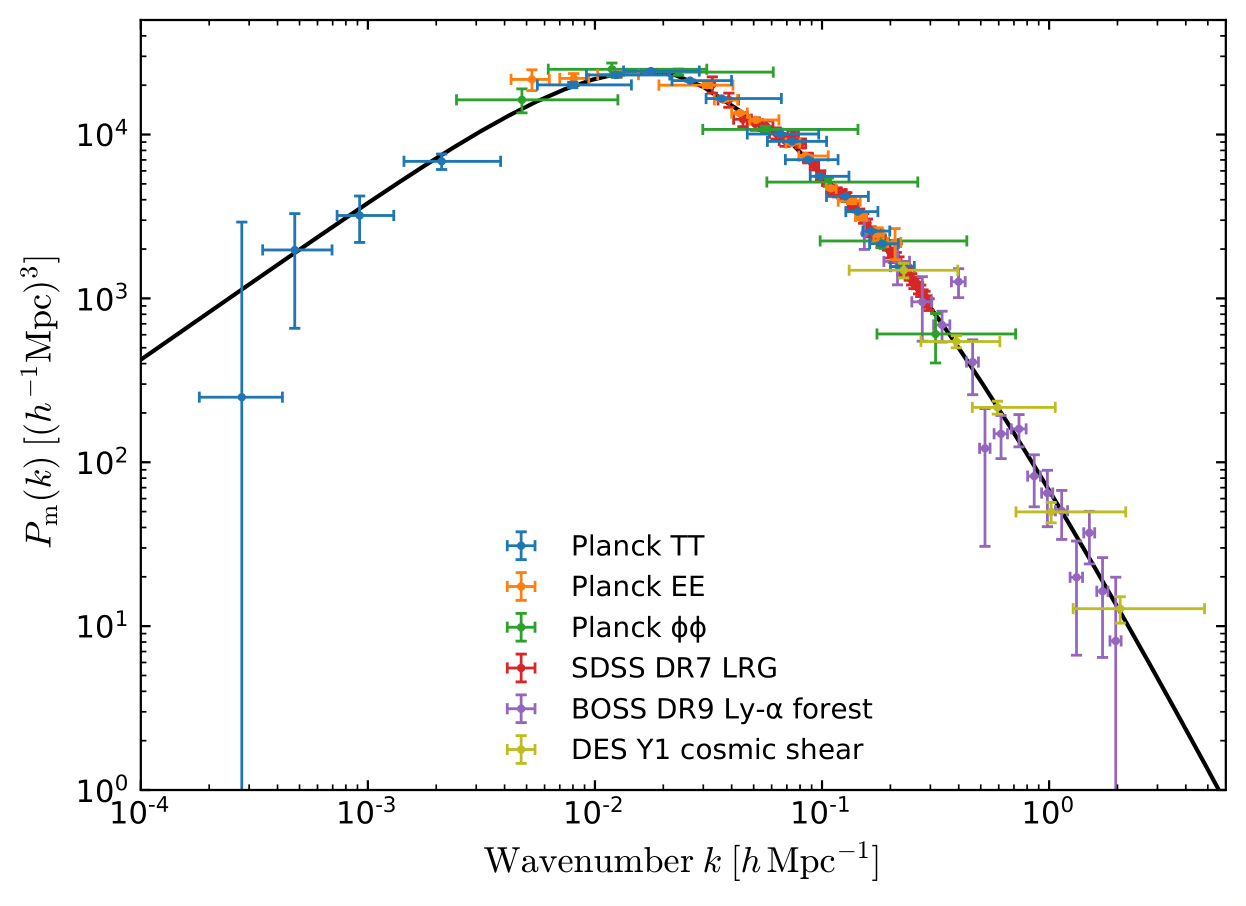
Credit: arxiv.org/abs/1807.06205Cosmological context
Bayes theorem:
We want to infer the parameters that generated an observation
Classical way of performing Bayesian Inference in Cosmology:
Power Spectrum
& Gaussian Likelihood


Cosmological context
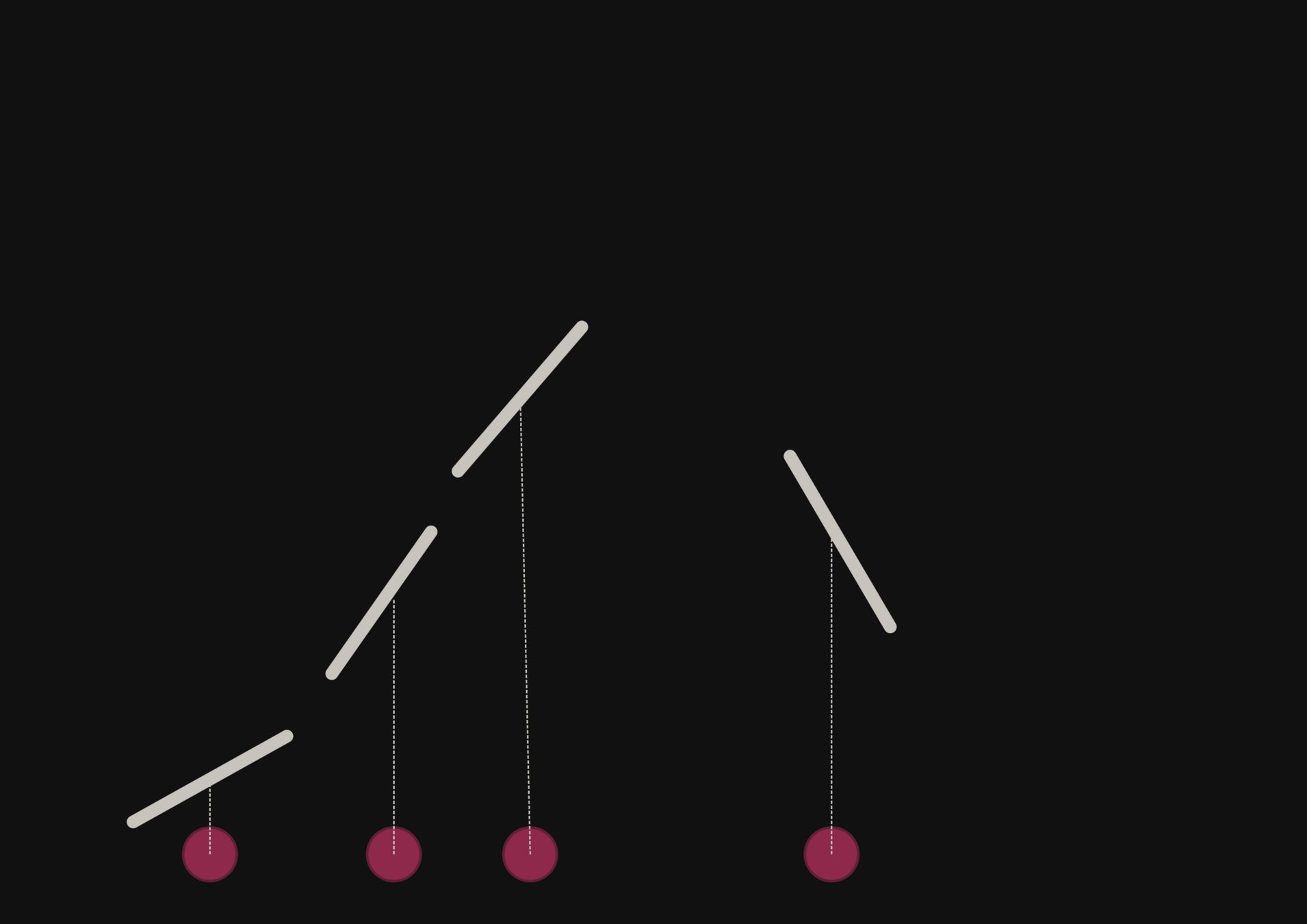
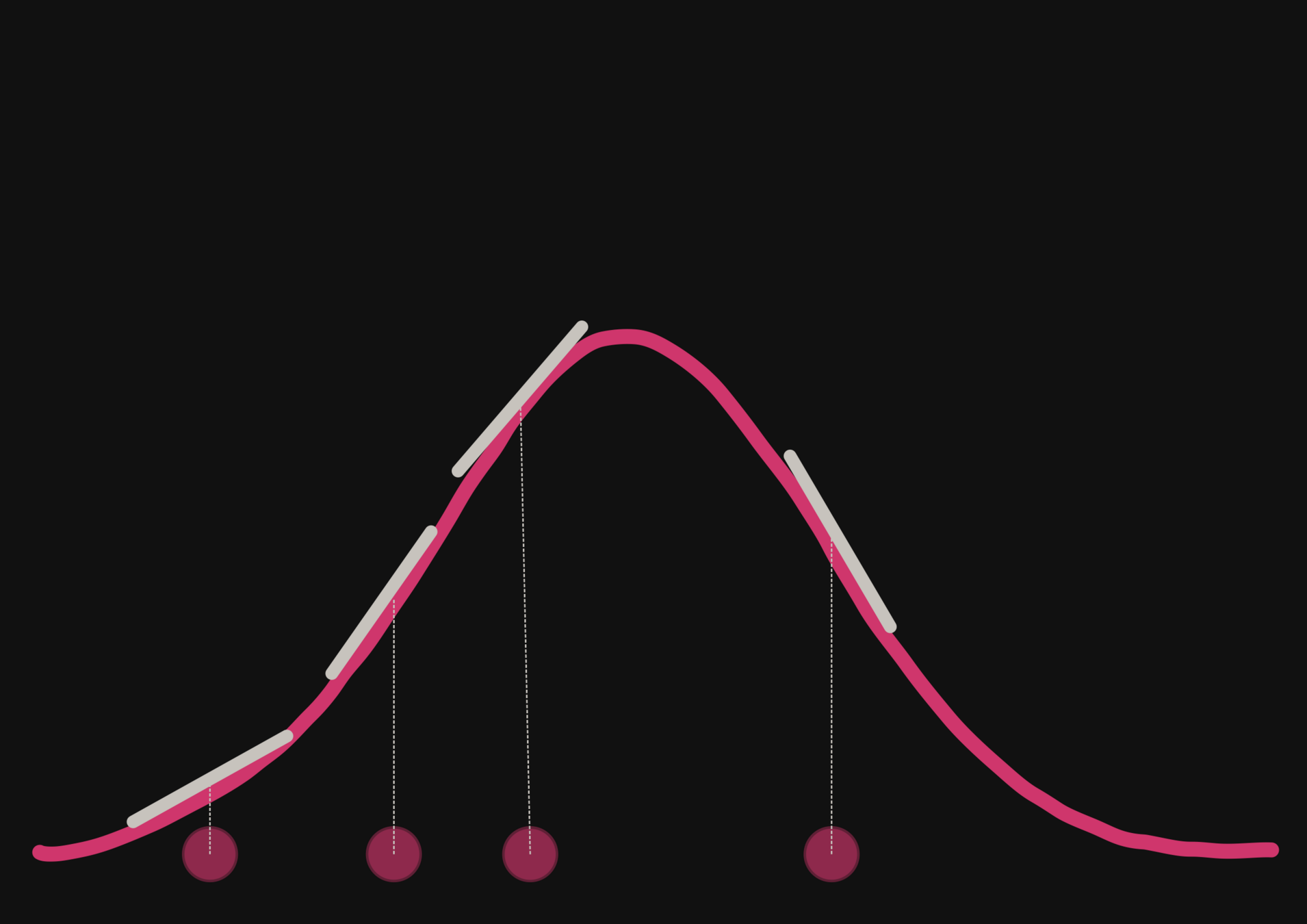
On large scales, the Universe is close to a Gaussian field and the 2-point function is a near sufficient statistic.
Cosmological context
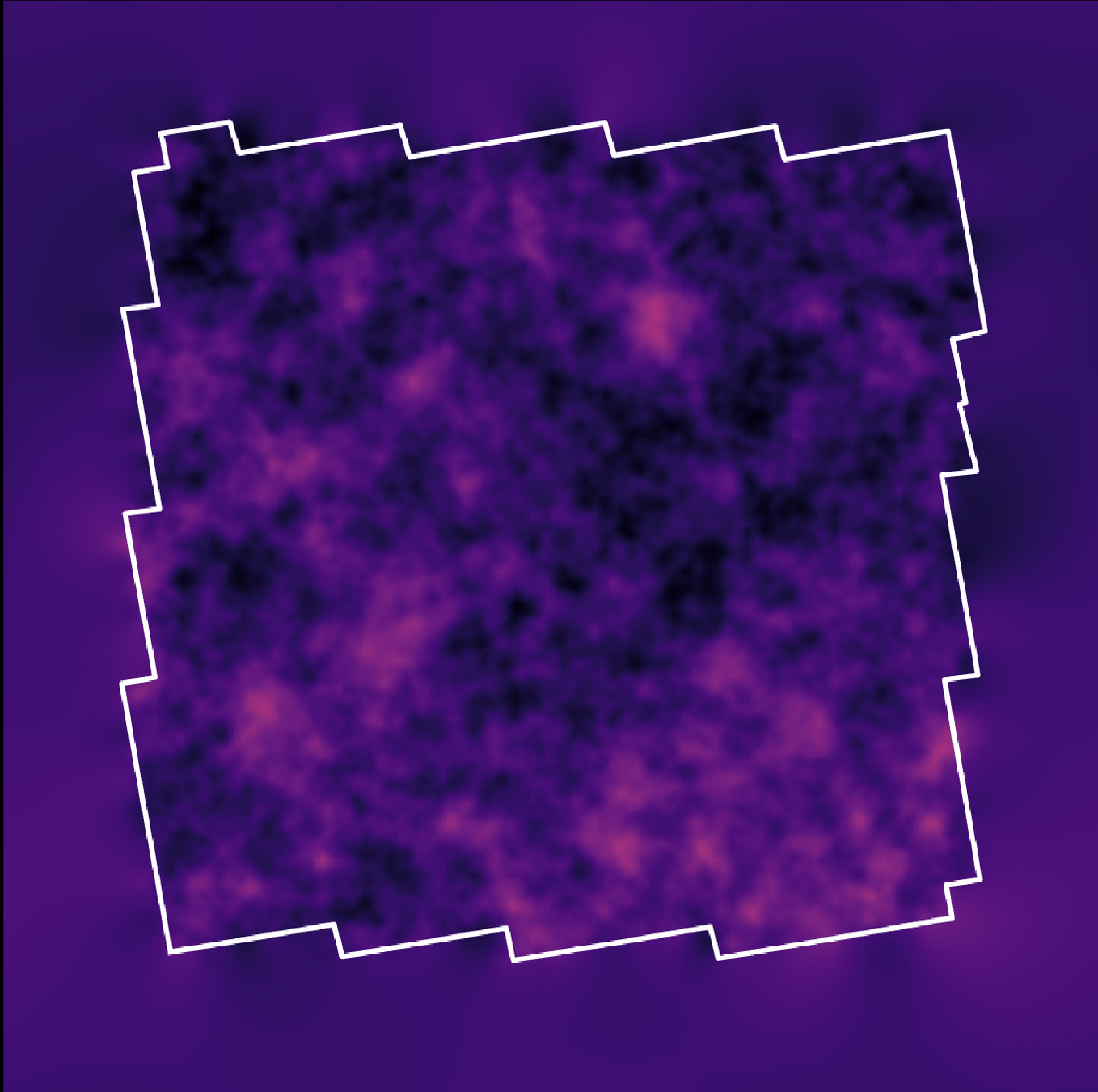
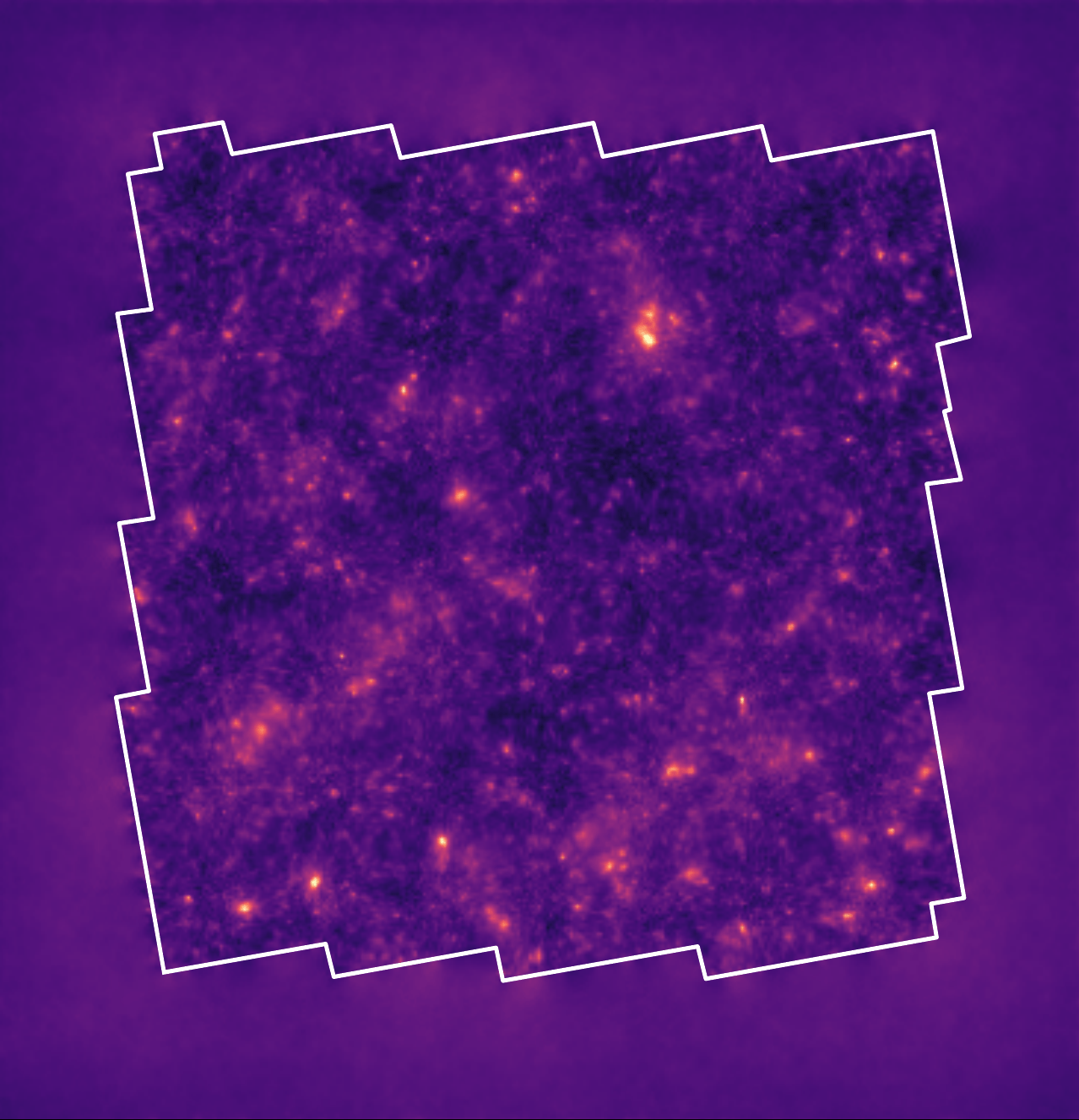
Credit: Benjamin RemyOn large scales, the Universe is close to a Gaussian field and the 2-point function is a near sufficient statistic.
Cosmological context

However, on small scales where non-linear evolution gives rise to a highly non-Gaussian field, this summary statistic is not sufficient anymore.

Credit: Benjamin RemyOn large scales, the Universe is close to a Gaussian field and the 2-point function is a near sufficient statistic.
However, on small scales where non-linear evolution gives rise to a highly non-Gaussian field, this summary statistic is not sufficient anymore.
Proof: full-field inference yield tighter constrain.
Cosmological context
How to do full-field inference?
Bayes theorem:
How to do full-field inference?
Bayes theorem:
How to do full-field inference?
Bayes theorem:
We can build a simulator to map the cosmological parameters to the data.
Simulator
How to do full-field inference?
Bayes theorem:
We can build a simulator to map the cosmological parameters to the data.
Simulator
How to do full-field inference?
Bayes theorem:
We can build a simulator to map the cosmological parameters to the data.

Simulator
How to do full-field inference?
Bayes theorem:
We can build a simulator to map the cosmological parameters to the data.
Prediction

Simulator
How to do full-field inference?
Bayes theorem:
We can build a simulator to map the cosmological parameters to the data.
Prediction

Simulator
Inference
How to do full-field inference?
How to do inference?

Simulator
How to do inference?
Depending on the simulator’s nature we can either perform
- Explicit inference
- Implicit inference

Simulator
Explicit inference
Explicit joint likelihood

Explicit simulator
Explicit inference
Explicit joint likelihood

Explicit simulator
Needs an explicit simulator to sample the joint posterior through MCMC:
Explicit inference
Explicit joint likelihood

Explicit simulator
Needs an explicit simulator to sample the joint posterior through MCMC:
→ gradient-based sampling schemes
Explicit inference
Explicit joint likelihood

Explicit simulator
Needs an explicit simulator to sample the joint posterior through MCMC:
→ gradient-based sampling schemes
Drawbacks:
- Evaluation of the joint likelihood
- Large number of (costly) simulations
- Challenging to sample (high dimensional, multimodal...)
- Usually, the forward model has to be differentiable
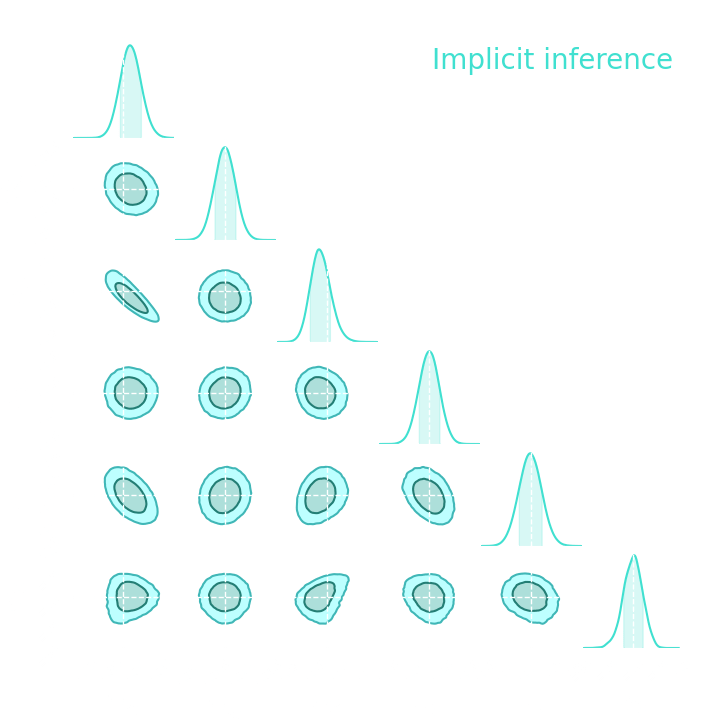
Implicit inference
Explicit joint likelihood

Explicit simulator
Implicit inference
Explicit joint likelihood

Explicit simulator

Simulator
Or
Implicit simulator
Implicit inference
Explicit joint likelihood

Explicit simulator

Simulator
Or
Because we only need simulations
Implicit simulator
Implicit inference
Because we only need simulations
This approach typically involve 2 steps:
Implicit inference
Because we only need simulations

This approach typically involve 2 steps:
Compressor
1) compression of the high dimensional data into summary statistics. Without losing information!
Implicit inference
Because we only need simulations
This approach typically involve 2 steps:

2) Implicit inference on this summary statistics to approximate the posterior.
1) compression of the high dimensional data into summary statistics. Without losing information!
Implicit inference
From a set of simulations we can approximate the
thanks to machine learning ..
- posterior
- likelihood ratio
- marginal likelihood
Implicit inference
The algorithm is the same for each method:
1) Draw N parameters
2) Draw N simulations
3) Train a neural network on to approximate the quantity of interest
4) Approximate the posterior from the learned quantity
Implicit inference
The algorithm is the same for each method:
1) Draw N parameters
2) Draw N simulations
3) Train a neural network on to approximate the quantity of interest
4) Approximate the posterior from the learned quantity
Implicit inference
The algorithm is the same for each method:
1) Draw N parameters
2) Draw N simulations
3) Train a neural network on to approximate the quantity of interest
4) Approximate the posterior from the learned quantity
We will focus on the Neural Likelihood Estimation and Neural Posterior Estimation methods
Neural Density Estimator


We need a model that can approximate distributions from its samples.
Easy to evaluate
Neural Density Estimator
We need a model that can approximate distributions from its samples.


Easy to evaluate
and sample
Neural Density Estimator
We need a model that can approximate distributions from its samples.


Easy to evaluate
and sample
Normalizing Flows
Normalizing Flows
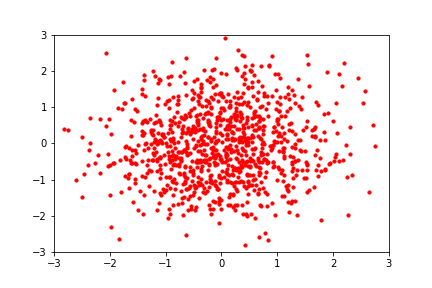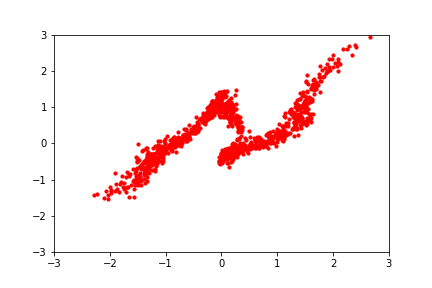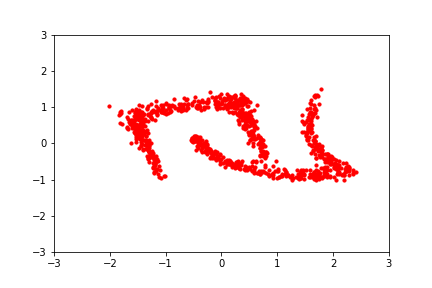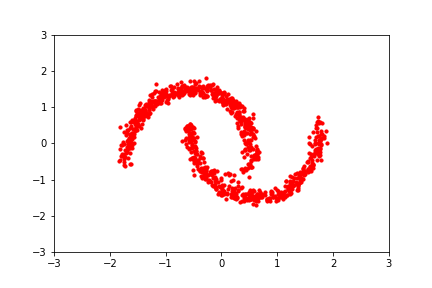
reference: https://blog.evjang.com/2019/07/nf-jax.html
Normalizing Flows


Normalizing Flows


Normalizing Flows


Normalizing Flows


Normalizing Flows


Normalizing Flows


Normalizing Flows


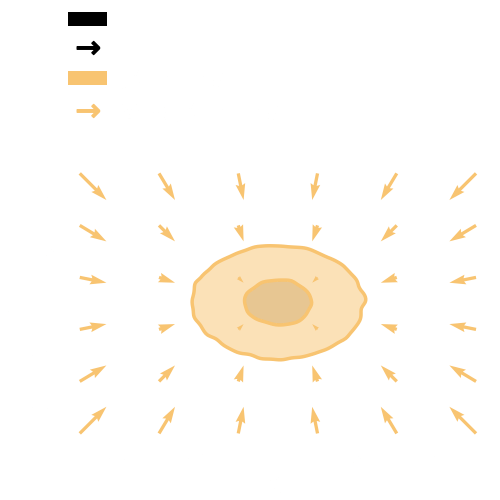
Change of Variable Formula:
Normalizing Flows


Change of Variable Formula:
Normalizing Flows


We need to learn the mapping
to approximate the complex distribution.
Normalizing Flows


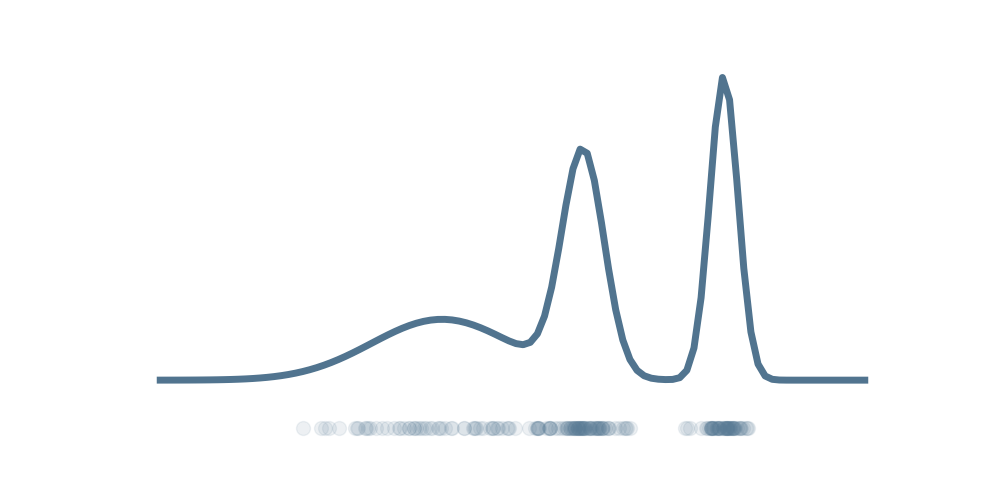

True distribution
We need to learn the mapping
to approximate the complex distribution.
Normalizing Flows




True distribution
It seems to be the one!
How to train a Normalizing Flow?
How to train a Normalizing Flow?
Variational parameters related to the mapping
How to train a Normalizing Flow?
How to train a Normalizing Flow?
How to train a Normalizing Flow?
How to train a Normalizing Flow?
How to train a Normalizing Flow?
From simulations of the true distribution only!
Normalizing Flows for Implicit Inference
This is super nice, it allows us to approximate the posterior distribution from simulations ONLY!
But simulations can sometimes be very expensive and training a NF requires a lot of simulations..
Neural Posterior Estimation with Differentiable Simulators
ICML 2022 Workshop on Machine Learning for Astrophysics
Justine Zeghal, François Lanusse, Alexandre Boucaud,
Benjamin Remy and Eric Aubourg

Explicit joint likelihood

Explicit joint likelihood

Explicit joint likelihood

Explicit joint likelihood


a framework for automatic differentiation following the NumPy API, and using GPU
probabilistic programming library
powered by JAX

Explicit joint likelihood


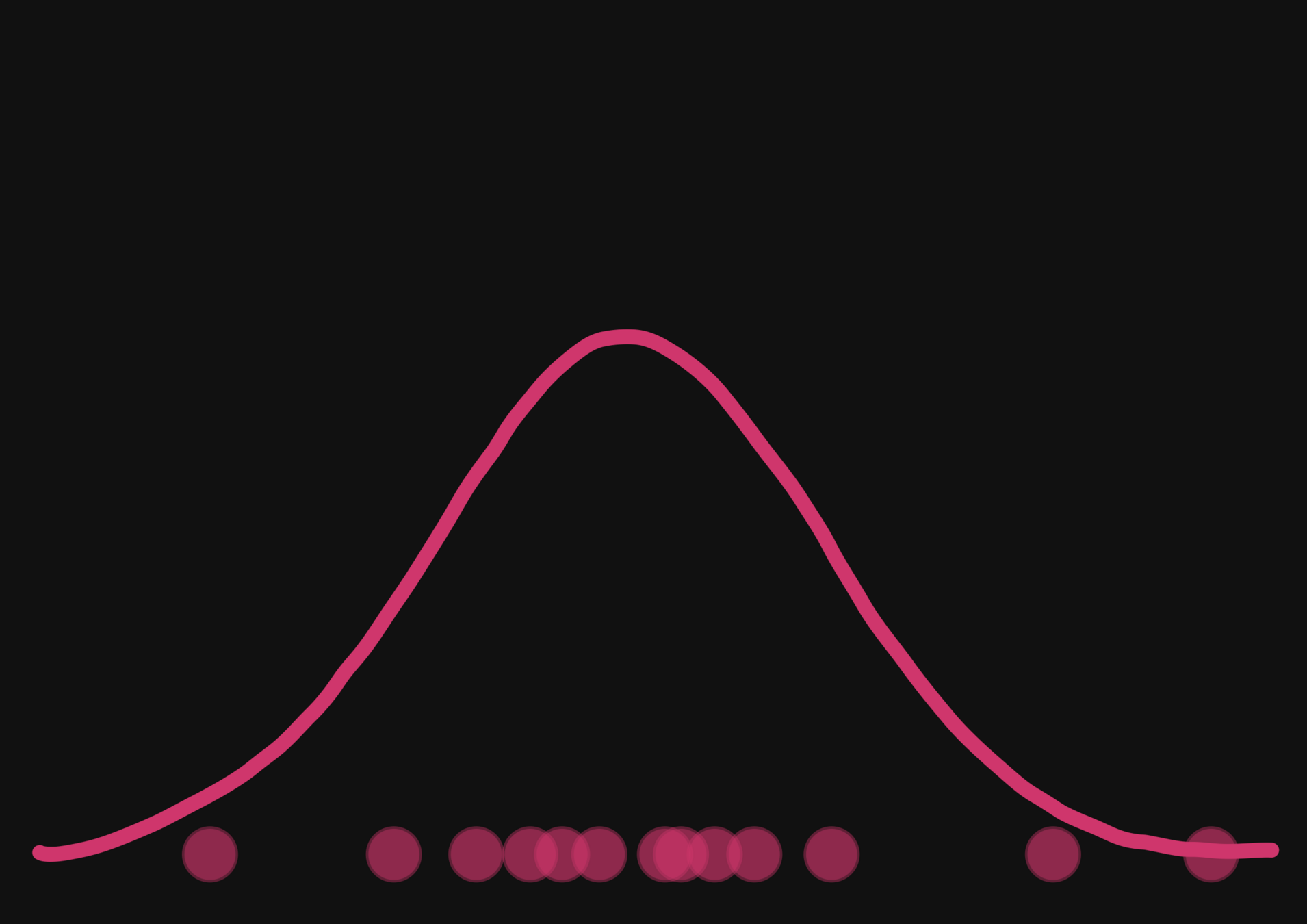

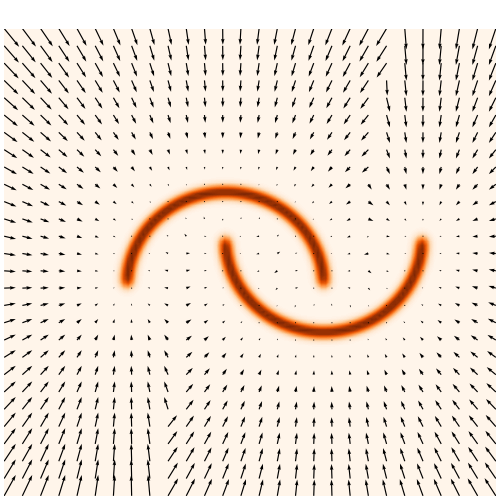
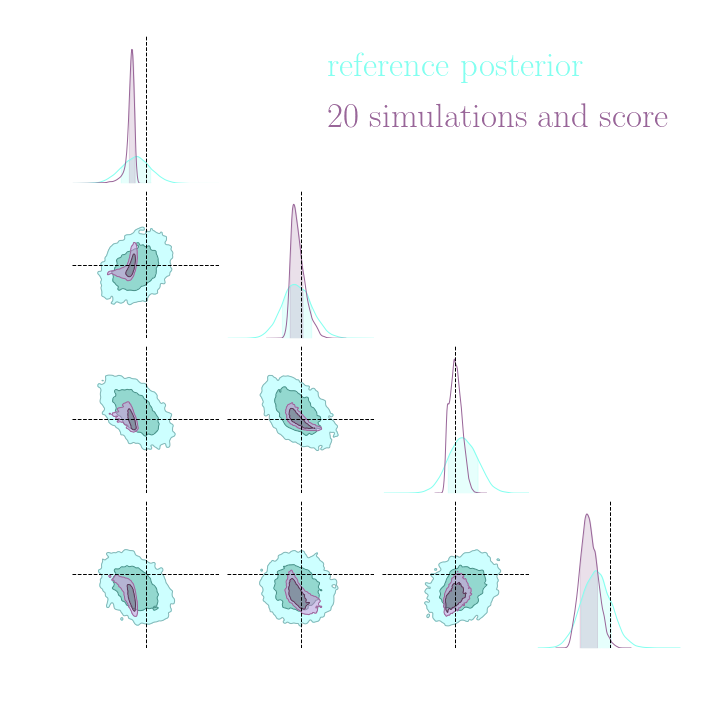
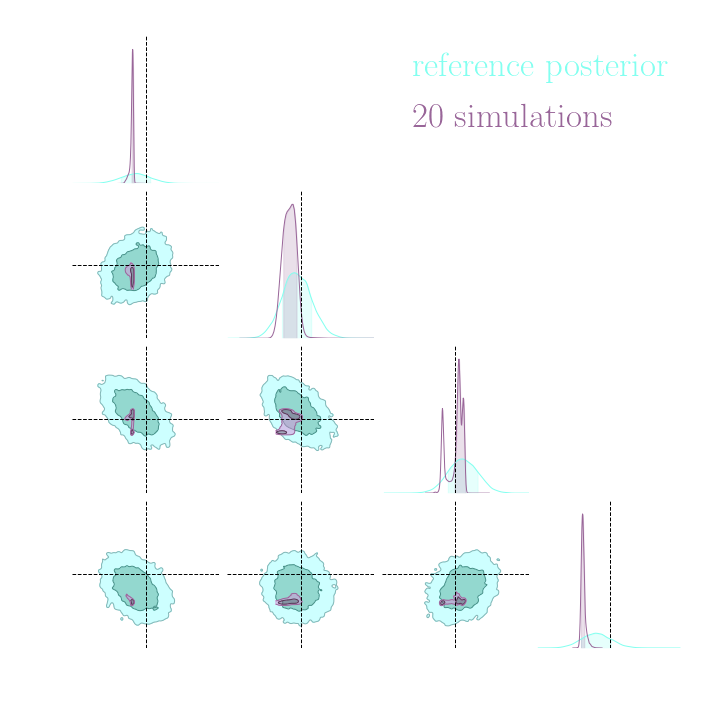
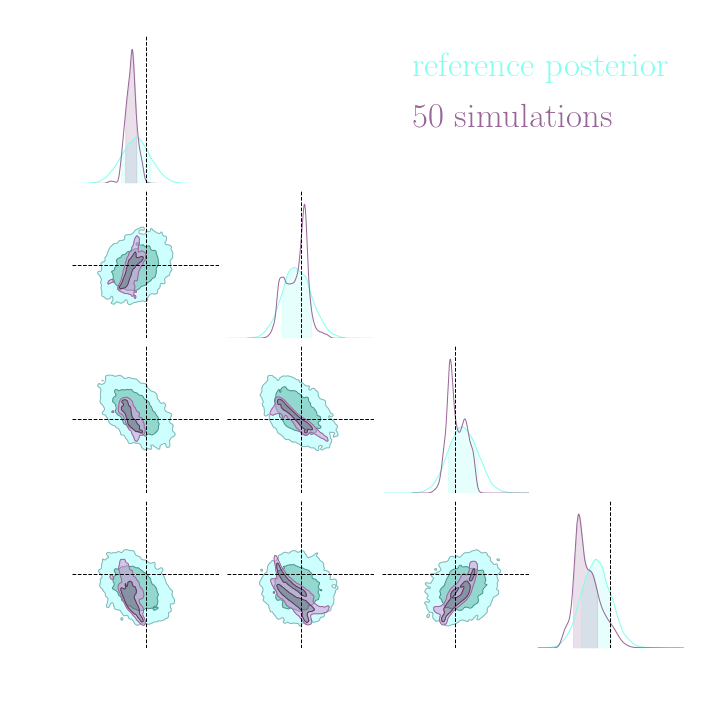
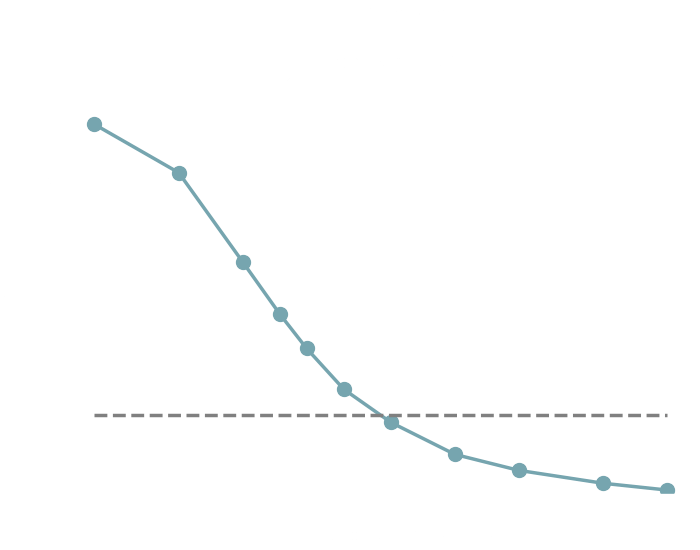
With a few simulations it's hard to approximate the posterior distribution.
→ we need more simulations
BUT if we have a few simulations
and the gradients
(also know as the score)
then it's possible to have an idea of the shape of the distribution.
How gradients can help Implicit Inference?
How to train NFs with gradients?
How to train NFs with gradients?
Normalizing flows are trained by minimizing the negative log likelihood:
How to train NFs with gradients?
But to train the NF, we want to use both simulations and gradient
Normalizing flows are trained by minimizing the negative log likelihood:
How to train NFs with gradients?
But to train the NF, we want to use both simulations and gradient
Normalizing flows are trained by minimizing the negative log likelihood:
How to train NFs with gradients?
But to train the NF, we want to use both simulations and gradient
Normalizing flows are trained by minimizing the negative log likelihood:
How to train NFs with gradients?
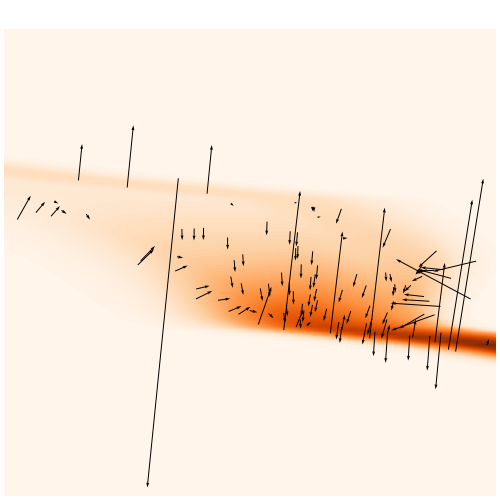
Problem: the gradient of current NFs lack expressivity
But to train the NF, we want to use both simulations and gradient
Normalizing flows are trained by minimizing the negative log likelihood:
How to train NFs with gradients?
Problem: the gradient of current NFs lack expressivity
But to train the NF, we want to use both simulations and gradient
Normalizing flows are trained by minimizing the negative log likelihood:
How to train NFs with gradients?

Problem: the gradient of current NFs lack expressivity
But to train the NF, we want to use both simulations and gradient
Normalizing flows are trained by minimizing the negative log likelihood:
How to train NFs with gradients?

Problem: the gradient of current NFs lack expressivity
But to train the NF, we want to use both simulations and gradient
Normalizing flows are trained by minimizing the negative log likelihood:
How to train NFs with gradients?

Problem: the gradient of current NFs lack expressivity
But to train the NF, we want to use both simulations and gradient
Normalizing flows are trained by minimizing the negative log likelihood:


Results on a toy model

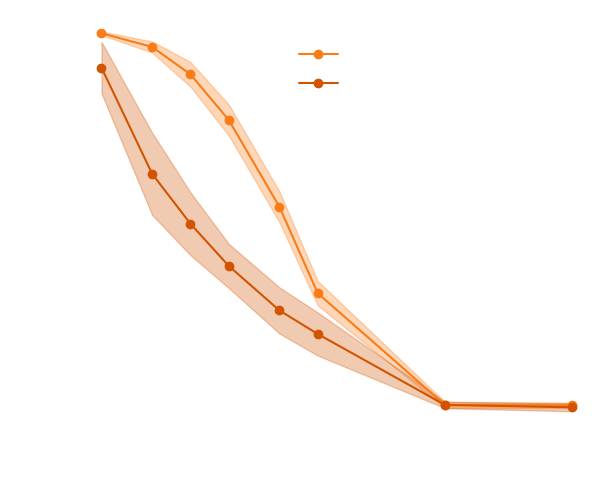
→ On a toy Lotka Volterra model, the gradients helps to constrain the distribution shape.
Results on a toy model
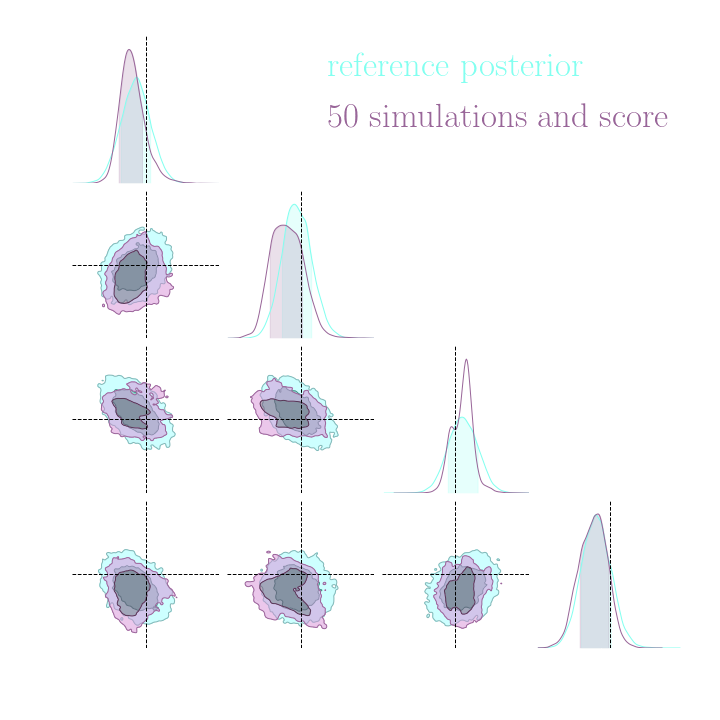
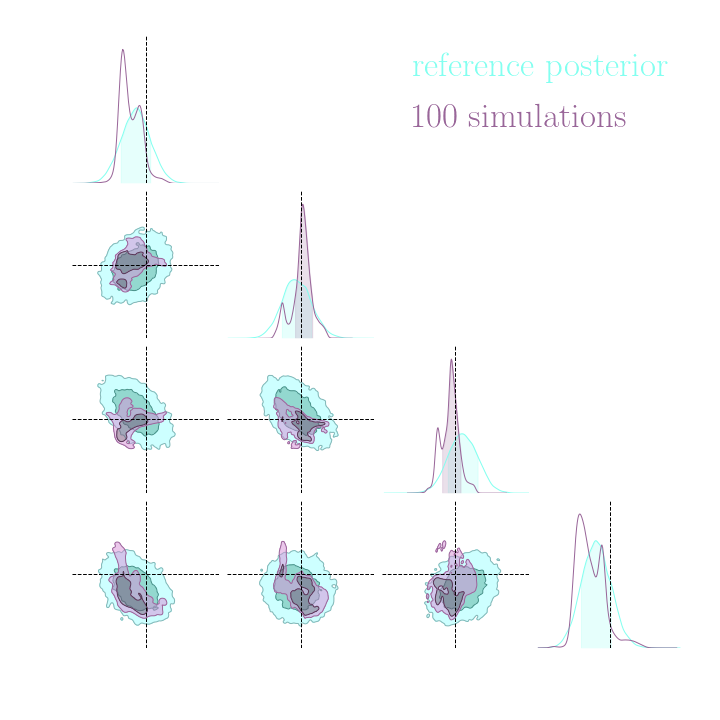
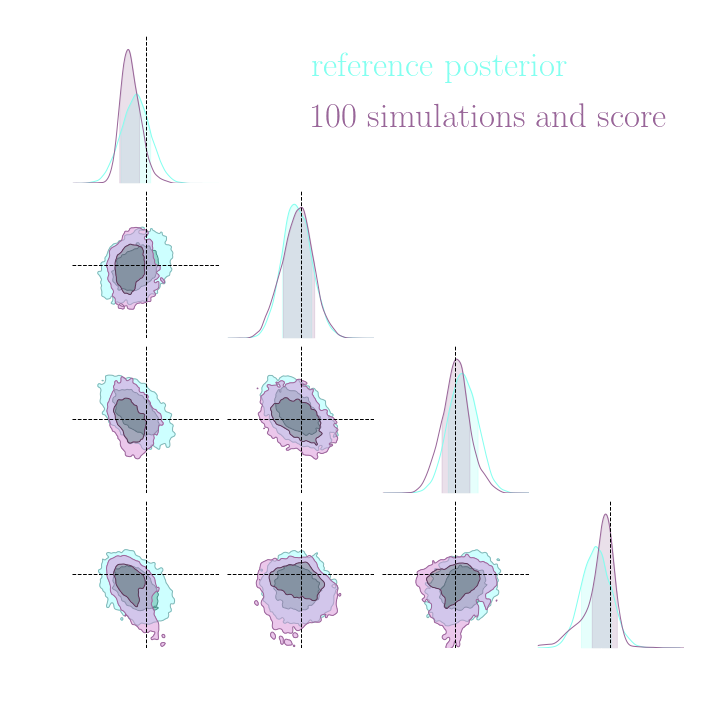
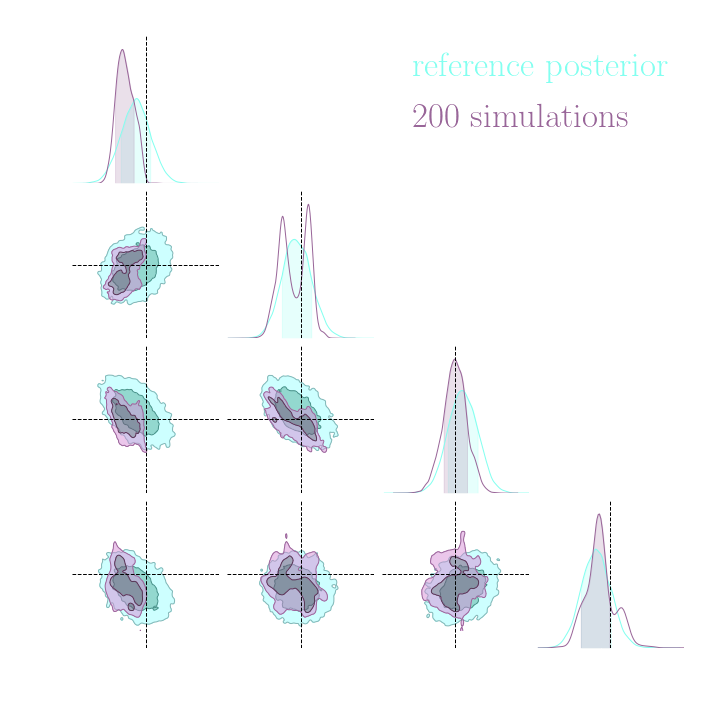
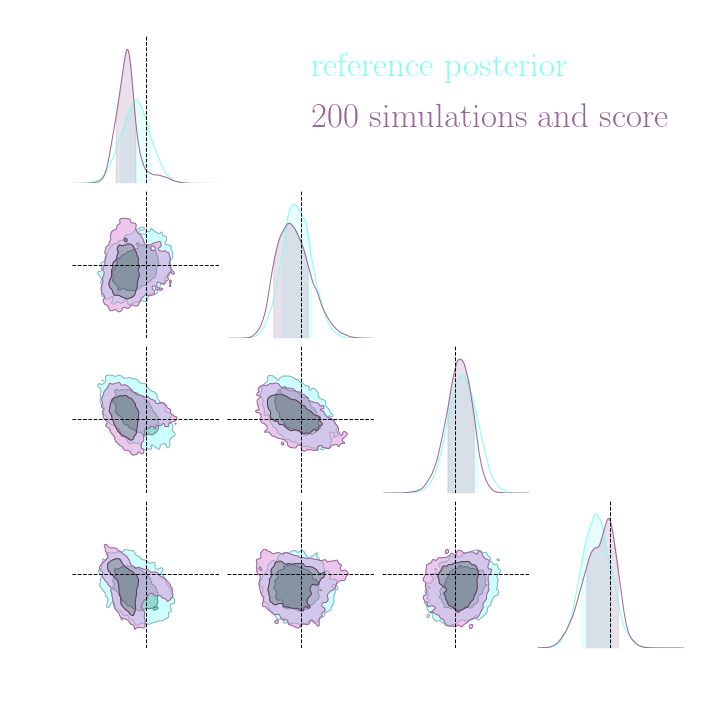
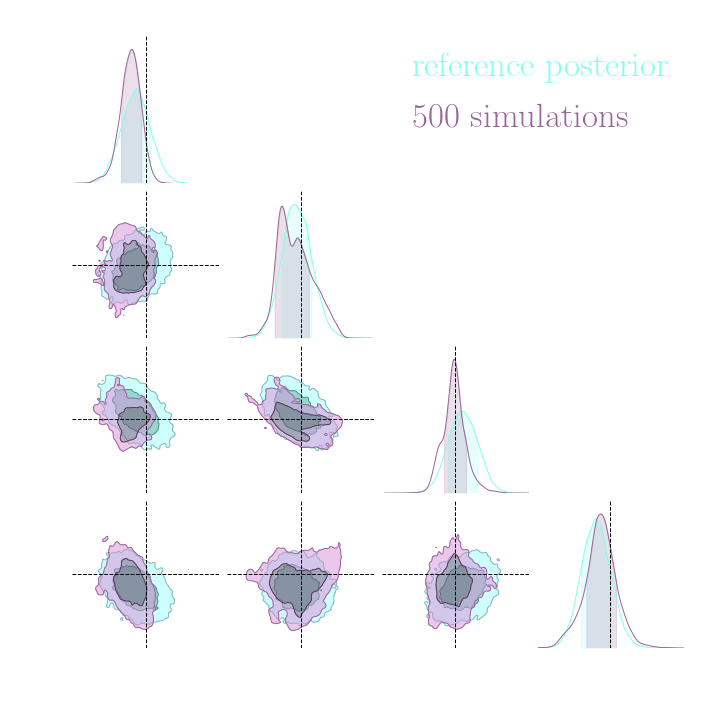
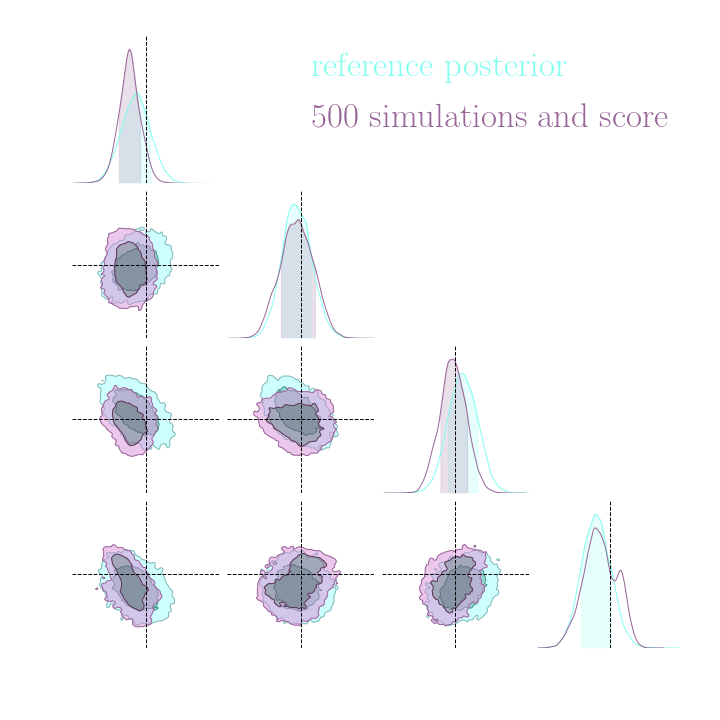
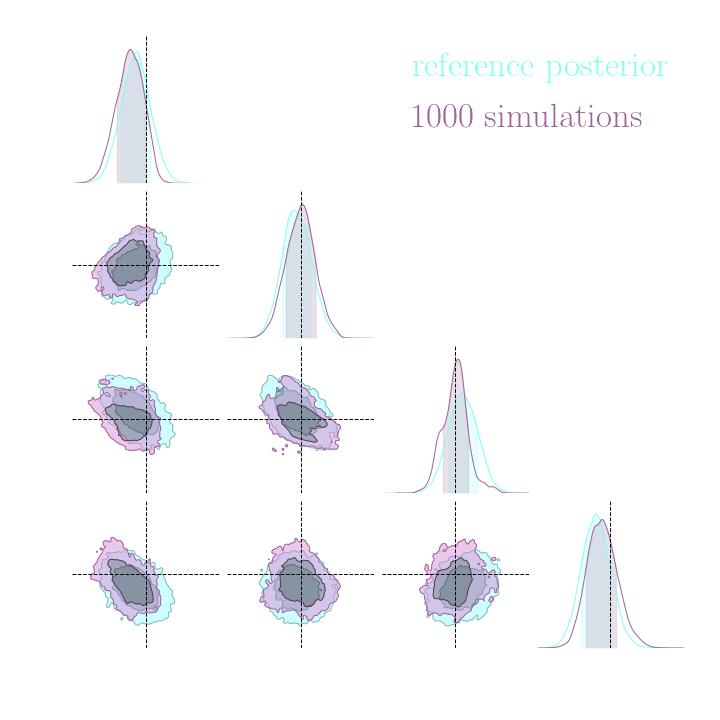
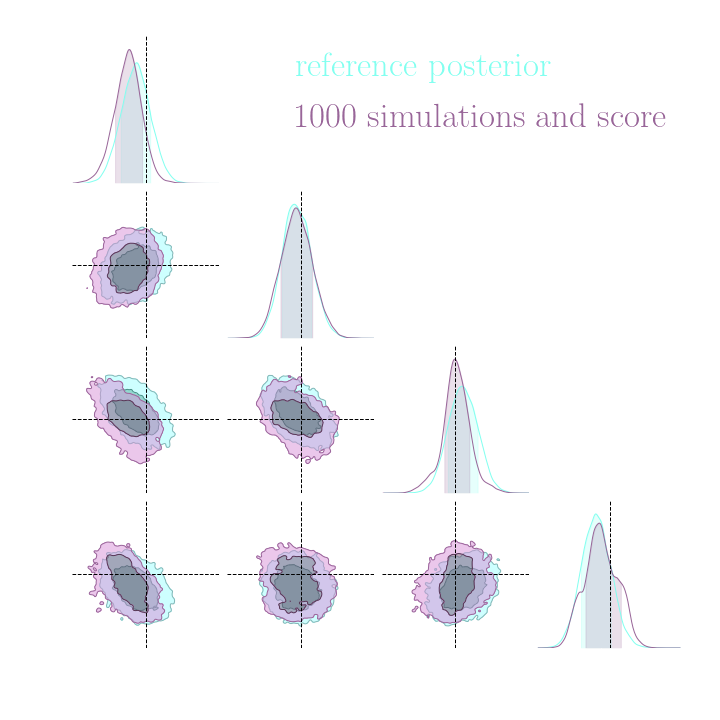
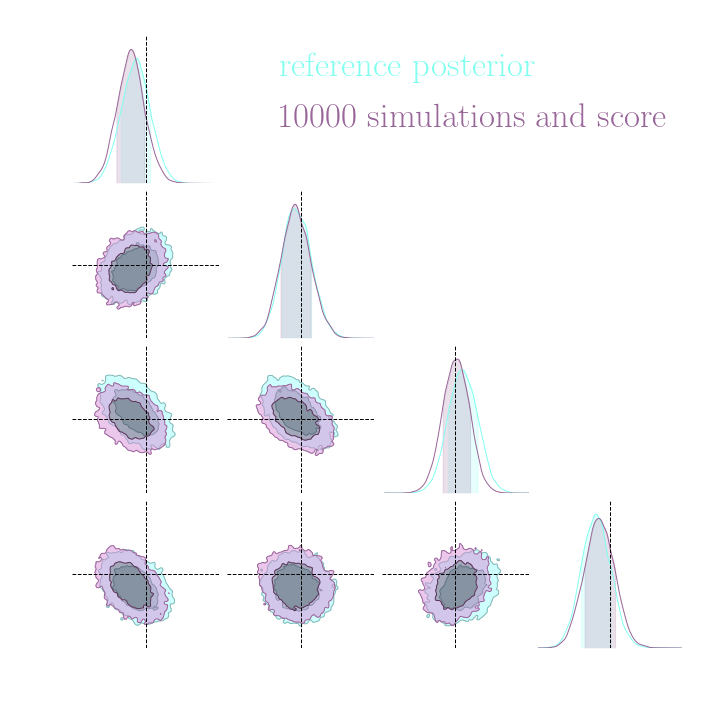
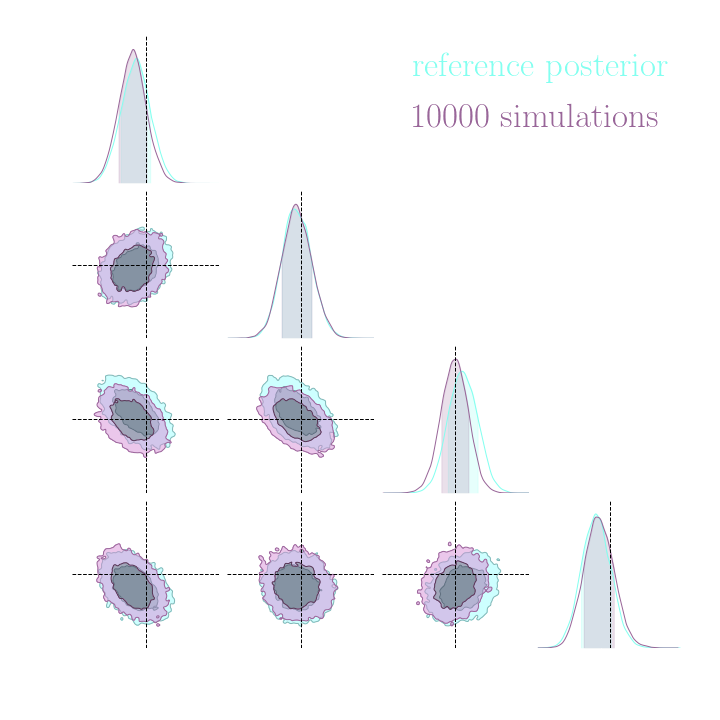
Simulation-Based Inference Benchmark for LSST Weak Lensing Cosmology
Justine Zeghal, Denise Lanzieri, François Lanusse, Alexandre Boucaud, Gilles Louppe, Eric Aubourg,
and The LSST Dark Energy Science Collaboration (LSST DESC)
-
do gradients help implicit inference methods?
In the case of weak lensing full-field analysis,
-
which inference method requires the fewest simulations?


We developed a fast and differentiable (JAX) log-normal mass maps simulator
For our benchmark: a Differentiable Mass Maps Simulator


-
Do gradients help implicit inference methods?
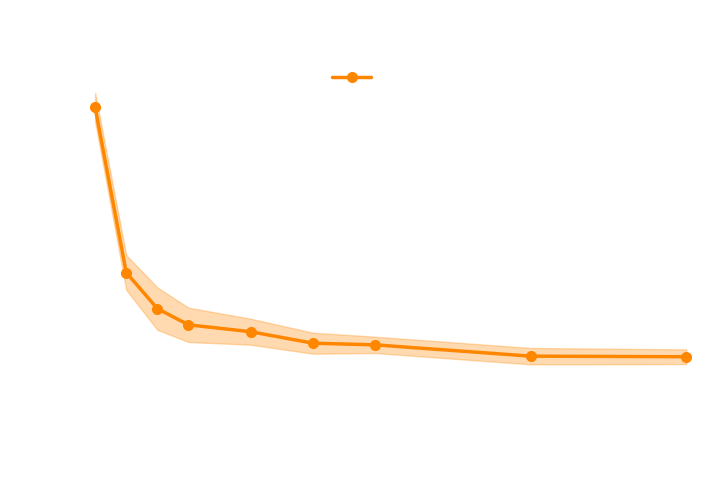
Training the NF with simulations and gradients:
Loss =
-
Do gradients help implicit inference methods?
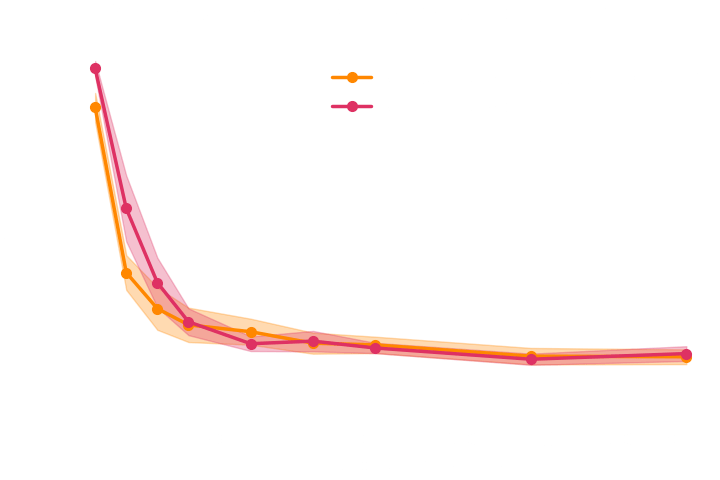
Training the NF with simulations and gradients:
Loss =
-
Do gradients help implicit inference methods?
(from the simulator)
(requires a lot of additional simulations)
→ For this particular problem, the gradients from the simulator are too noisy to help.
-
Do gradients help implicit inference methods?
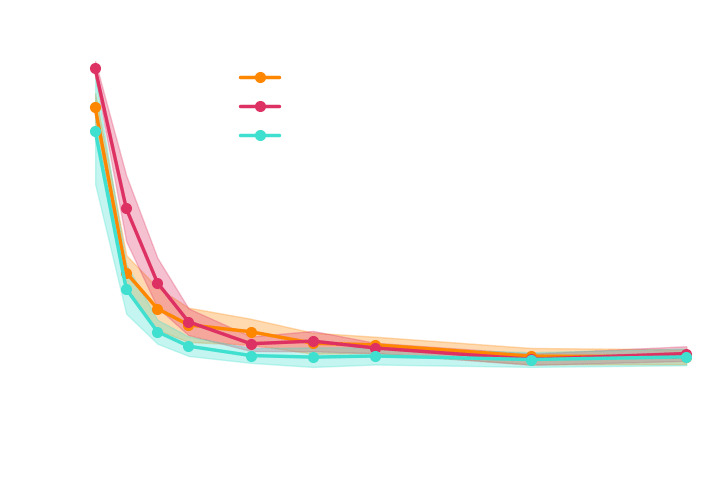
→ Implicit inference (NLE) requires 1500 simulations.
→ Better to use NLE without gradients than NLE with gradients.

-
Which inference method requires the fewest simulations?
→ Implicit inference (NLE) requires 1500 simulations.
→ What about explicit inference?
→ Explicit inference requires 10^5 simulations.
simulations
simulations
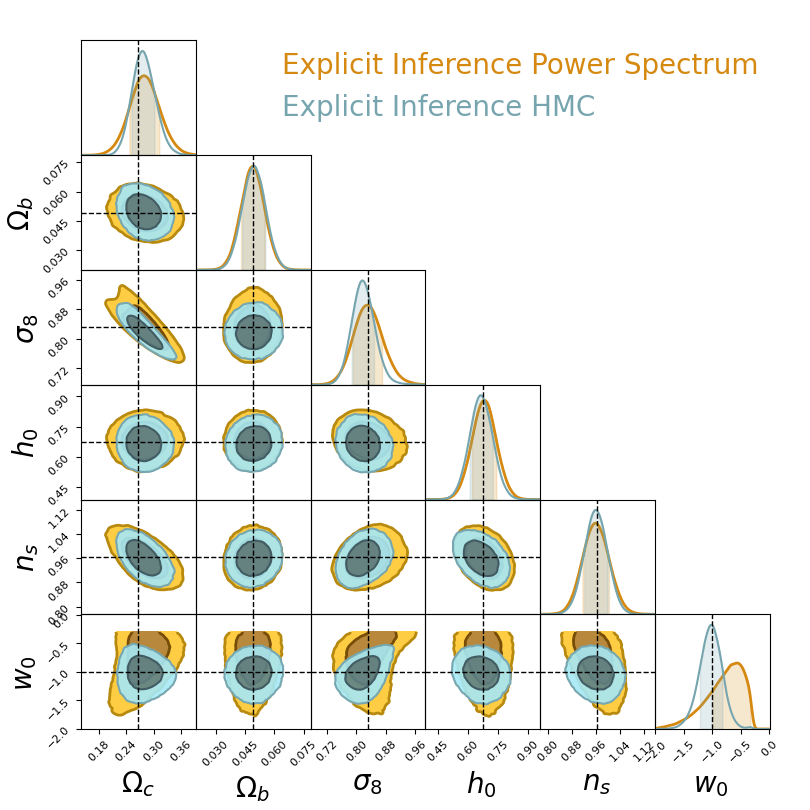
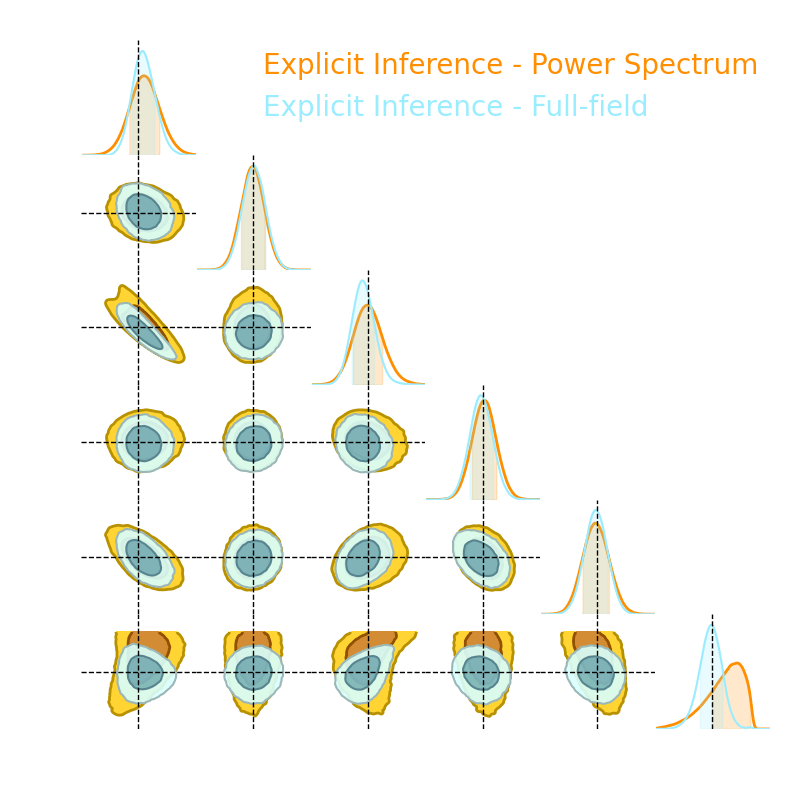
→ Explicit and implicit full-field inference yields the same posterior.
→ Explicit full-field inference requires 630 000 simulations (HMC in high dimension)
→ Implicit full-field inference requires 1 500 simulations
+ a maximum of 100 000 simulations to build
sufficient statistics
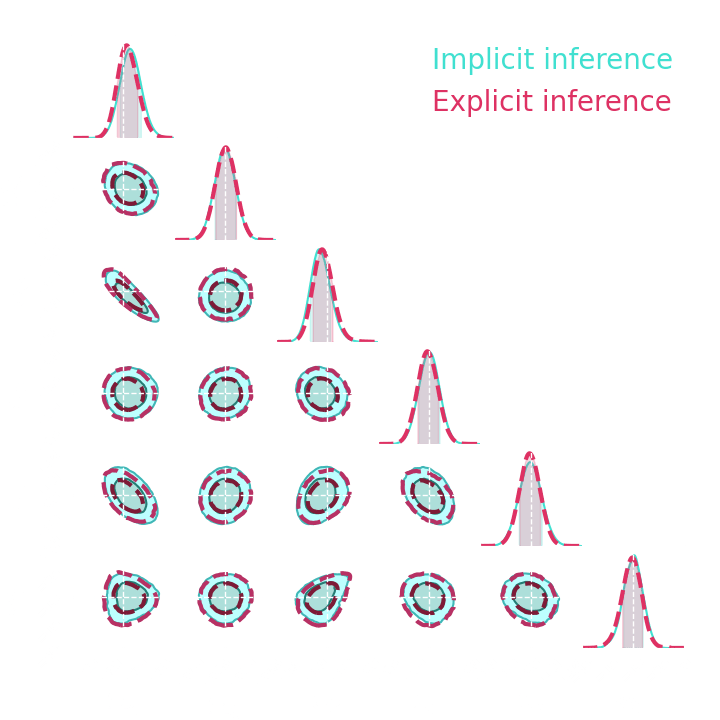
-
Which inference method requires the fewest simulations?
Optimal Neural Summarisation for Full-Field Weak Lensing Cosmological Implicit Inference
Denise Lanzieri, Justine Zeghal, T. Lucas Makinen, François Lanusse, Alexandre Boucaud and Jean-Luc Starck
Summary statistics

Simulator
Summary statistics

Simulator
Summary statistics

Simulator


How to extract all the information?
It is only a matter of the loss function you use to train your compressor..
Two ways..
1) Regression
Which learns a moment of the posterior distribution and is not guaranteed to be sufficient.
Two ways..
1) Regression
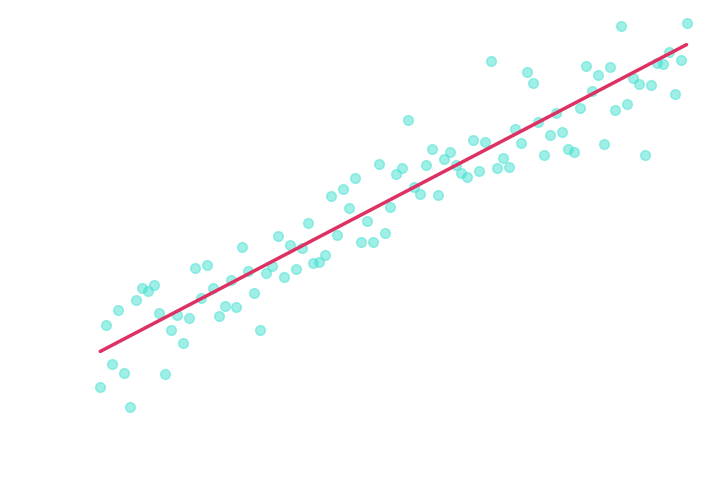
Which learns a moment of the posterior distribution and is not guaranteed to be sufficient.
Two ways..
1) Regression
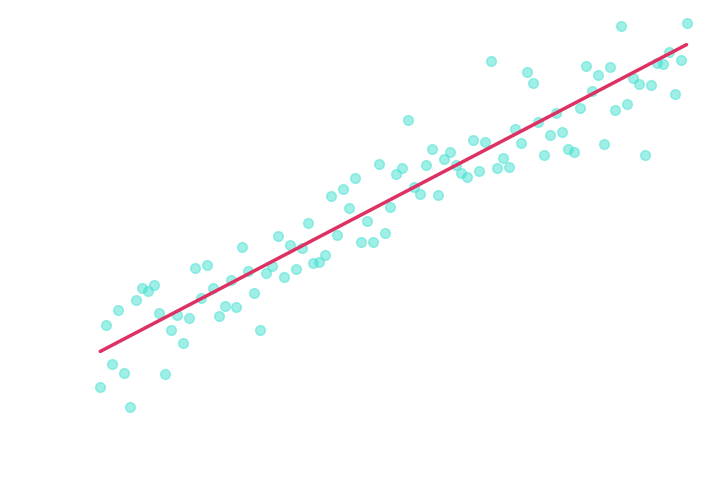
Which learns a moment of the posterior distribution and is not guaranteed to be sufficient.
Two ways..
1) Regression




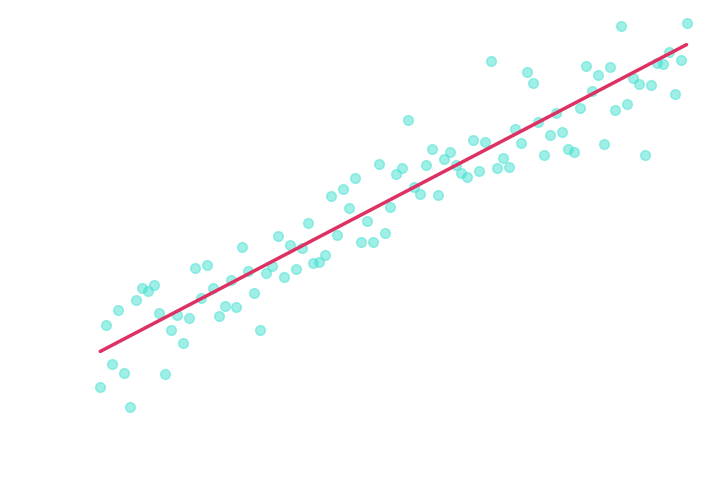
Which learns a moment of the posterior distribution and is not guaranteed to be sufficient.
Two ways..
1) Regression





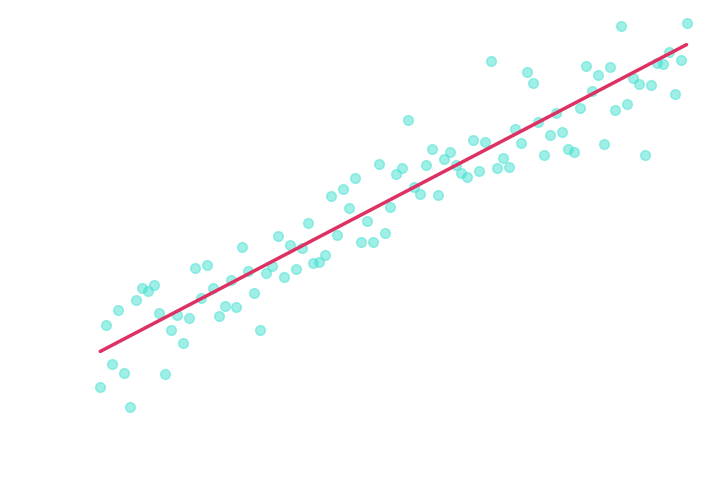
Which learns a moment of the posterior distribution and is not guaranteed to be sufficient.
Two ways..
1) Regression






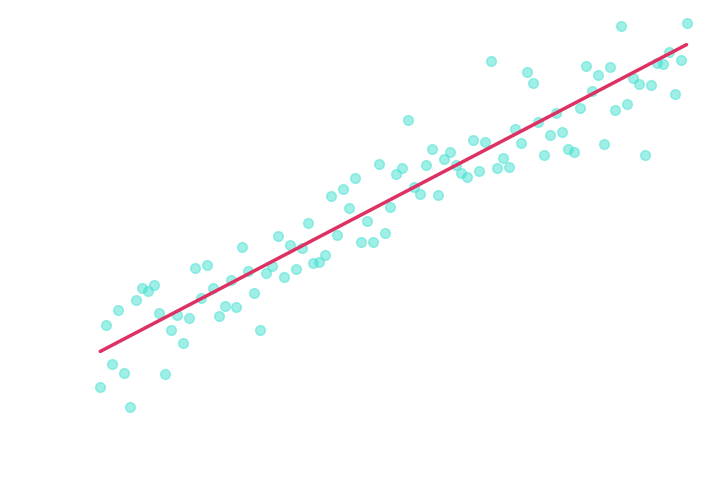
Which learns a moment of the posterior distribution and is not guaranteed to be sufficient.
Two ways..
1) Regression



Not a sufficient statistics
Which learns a moment of the posterior distribution and is not guaranteed to be sufficient.
Two ways..
1) Regression
Two ways..
2) Mutual information maximization
Two ways..
2) Mutual information maximization
Two ways..
2) Mutual information maximization
Two ways..
2) Mutual information maximization
Two ways..
2) Mutual information maximization
Two ways..
2) Mutual information maximization
Two ways..
2) Mutual information maximization
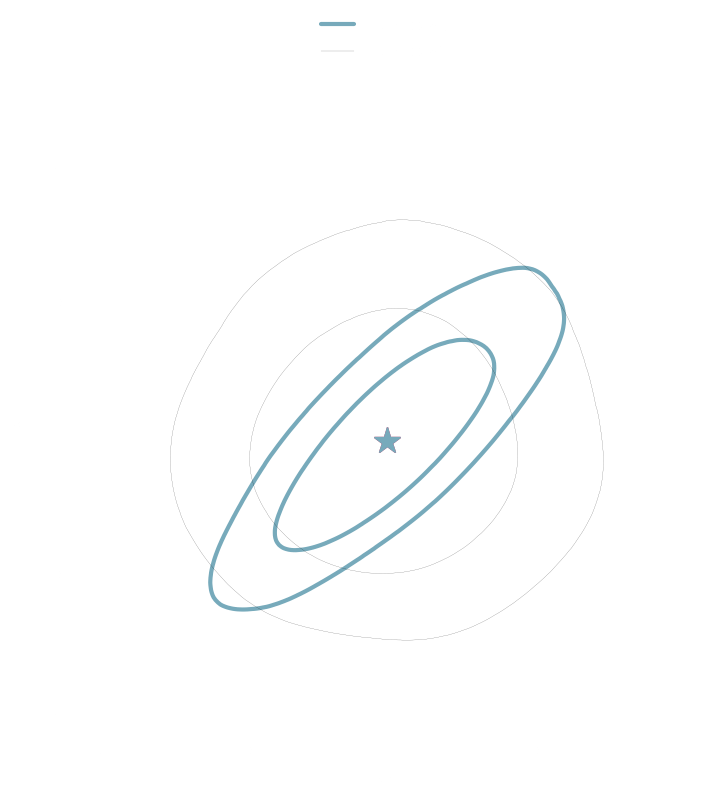
→ should build sufficient statistics
For our benchmark
Log-normal LSST Y10 like
differentiable
simulator



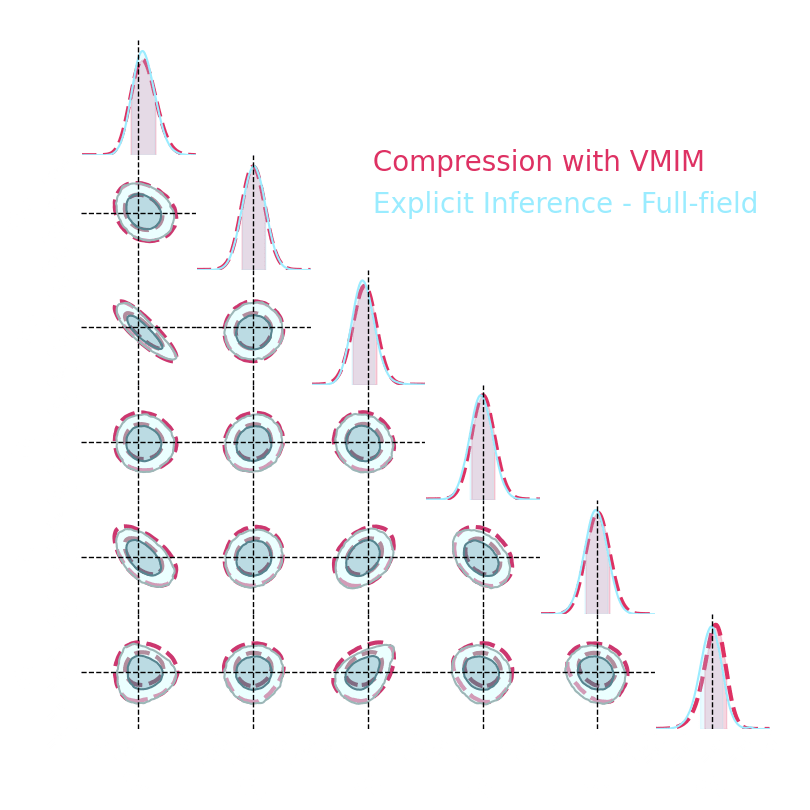
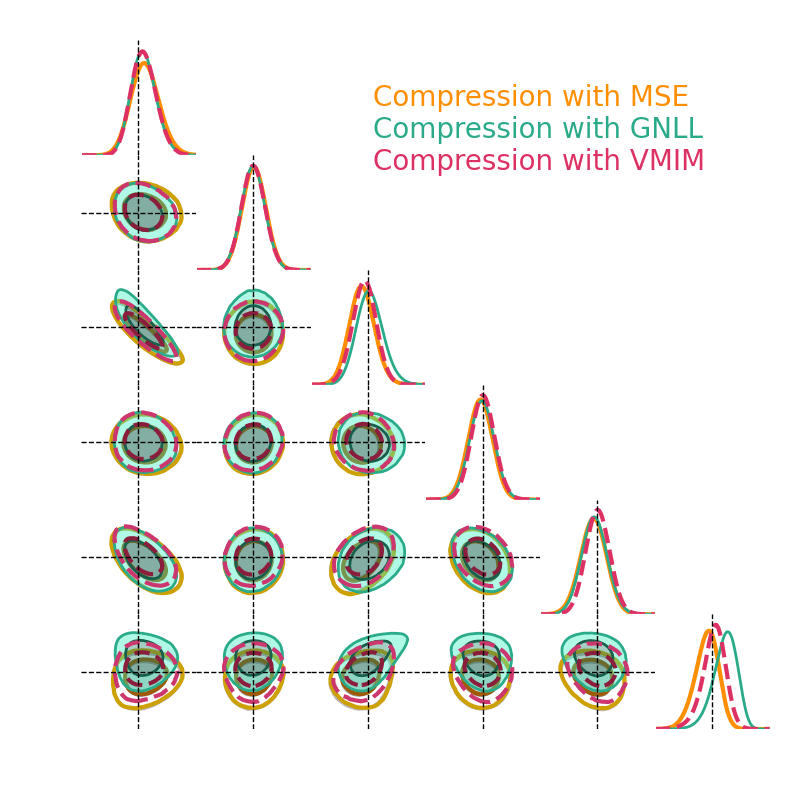
1. We compress using one of the 4 losses.
Benchmark procedure:
2. We compare their extraction power by comparing their posteriors.
For this, we use a neural-based likelihood-free approach, which is fixed for all the compression strategies.
Numerical results
compression schemes based on regression losses are not guaranteed to build such sufficient statistics
Takeaways
Compression schemes based on information maximization can build sufficient statistics
while
Summary
Summary

Explicit likelihood
Summary

Explicit likelihood

Simulator
Implicit likelihood
Summary
Explicit likelihood
Implicit likelihood

Simulator
Explicit inference
or
Implicit inference
Summary
Explicit likelihood
Implicit likelihood
Implicit inference
Explicit inference
or
Implicit inference
Summary
Implicit inference
Explicit inference
Summary
Implicit inference
Explicit inference
- MCMC in high-dimension
- Challenging to sample
- Needs the gradients
- simulations (on our problem)
Summary
Implicit inference
Explicit inference
- MCMC in high-dimension
- Challenging to sample
- Needs the gradients
- simulations (on our problem)
- Based on machine learning
- Only need simulations
- Gradients can be used but do not help in our problem
- simulations (on our problem)
- Better to do one compression step before (Mutual information maximization)
Summary
Implicit inference
Explicit inference
- MCMC in high-dimension
- Challenging to sample
- Needs the gradients
- simulations (on our problem)
- Based on machine learning
- Only need simulations
- Gradients can be used but do not help in our problem
- simulations (on our problem)
- Better to do one compression step before (Mutual information maximization)


Simulator
Summary statistics

Thank you for your attention!
Rencontres Statistiques Lyonnaises
By Justine Zgh
Rencontres Statistiques Lyonnaises
- 145



