R

E

A

C

T

O

xamples 

epeat

ode

pproach

ptimize

est

Cyclic Linked List

Problem

Given the head of a singly linked list, determine if there is a cycle within the linked list. If there is a cycle, return true and log the length of the cycle and the first node in the cycle. If there is no cycle, return false.

Here's the catch:

You canNOT use any additional data structures, including modifying the existing data structure. No arrays, no objects, no maps, no linked lists, etc.

Keep in mind...

The linked list constructor is already provided for you - therefore you canNOT modify the linked list/properties on the node.

Also remember that the nodes in the linked list can have the same values.

Build the CyclicList

function Node (value) {
    this.value = value;
    this.next = null;
}

function BuildLinkedList (linkedListLength, cycleLength) {
    if (cycleLength >= linkedListLength) {
        throw new Error('cycleLength must be smaller than linkedListLength');
    }
    var newNode;
    var startNode =  new Node(randomNum());
    this.head = startNode;
    var previous = startNode;

    for (var i = 1; i < linkedListLength; i++) {
        newNode = new Node(randomNum());
        previous.next = newNode;
        previous = newNode;
        if (i === linkedListLength - cycleLength) {
            var startingNodeOfCycle = newNode; 
        }
    }
    newNode.next = startingNodeOfCycle;
}

function randomNum() {
    return Math.floor(Math.random() * 100) + 1;
}

Example of a linked list

var linkedList = new BuildLinkedList(6, 3)

where the list starts cycling through

Any ideas?

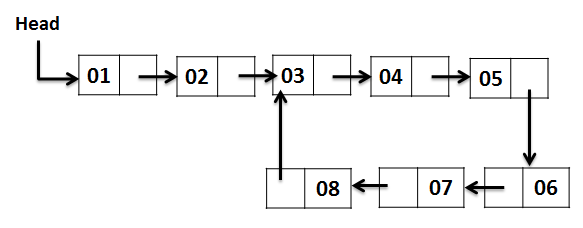
True

Length: 6

Start Node: 3

• Space complexity is 2 -- constant and constantly 2
• Which 2 things might we look at? 
• What if we advance them at different speeds?

*Hints*

1. Instantiate a slowNode to point to the startNode.
2. Instantiate a fastNode to point to the node AFTER the startNode.
3. Advance the slowNode one node at a time. 
4. Advance the fastNode two nodes at a time.
5. At each iteration, check if their values are equal. 
   1. If they're equal, you have found a cycle.

The runner technique

function detectLoop (linkedList) {
    var startNode = linkedList.head
    // An empty list has no cycles
    if (startNode === null || startNode.next === null) {
        return false;
    }

    var slowNode = startNode,
        fastNode = startNode.next;

    while(fastNode !== null) {
        slowNode = slowNode.next;

        if (fastNode.next === null) {
            return false;
        }

        fastNode = fastNode.next.next;

        if (slowNode === fastNode) {
            console.log(findCycleLength(slowNode), 
                findStartOfCycle(startNode,findCycleLength(slowNode)))
            return true; 
        }
    }
    return false;
}

Detecting a cycle

1. Make two pointers, both pointing to the same node in the cycle.
2. Keep one pointer stationary.
3. Move the second pointer one node at a time, counting each node, until the stationary pointer is reached.

Now: Determine cycle length

Hints below

Determine cycle length

A solution

1. Instantiate a new slowNode and fastNode at the original startNode.
2. Using the length of the cycle you just found, advance the fastNode that number of nodes.
3. Increment both the fastNode and the slowNode one node at a time, until they are equal. Once equal, you have the starting node of the cycle. 

Find start of cycle

Hints below

function findStartOfCycle(startNode, cycleLength) {
    var fastNode = startNode,
        slowNode = startNode;

    for (var i = 0; i < cycleLength; i++) {
        fastNode = fastNode.next;
    }

    while (fastNode !== slowNode) {
        fastNode = fastNode.next;
        slowNode = slowNode.next;
        if (fastNode === slowNode) {
            return fastNode;
        }
    }
}

Find start of cycle

Solution below

Explanation

Why does this work?

Why do we start N nodes in to the linked list

(N representing the length of the cycle)?

Well, imagine that you have a first pointer at the head of the LL and a second pointer at the second node. As you increment the pointers one node at a time, they will always be adjacent to each other. Now let's start over, keeping the first pointer at the head, but point the second pointer to the 3rd node. As we increment, this yields a distance of one node between them. Now let's increase the second pointer to the 4th node. As we increment, this yields a distance of two nodes between them. As we continually increase the distance between them, eventually reaching the length of the cycle, as we increase the pointers, we will eventually reach the point where they overlap at the start node of the cycle.