Group Theory, Irreducible Representations, and Tensor Products

and How to Use them in e3nn to Build Euclidean Neural Networks

Mario Geiger

MRS Fall Meeting Tutorial

This talk is about

1. The math of rotations and parity
    
2. Creating and manipulating equivariant functions (polynomials)
   Which is useful for
   1. Compute spherical harmonics
   2. Create invariant polynomials (Thomas and Martin talk)
   3. Create the linear part of equivariant neural networks
       
3. Non linearities (non-polynomial)
   Which is useful for
   1. For the activation functions of the neural networks

Polynomial part

1. Define properly what is an equivariant polynomial
2. Give the tools to create them

Examples and Code

1. Spherical Harmonics
2. Tensor Product with weights (cornerstone of e3nn)
3. Decomposition of Cartesian Tensors

Nonlinearities

1. Gates

Group and Representations

Group and Representations

"what are the operations"

"how they compose"

Group and Representations

"what are the operations"

"how they compose"

"vector spaces on which the action of the group is defined"

Group and Representations

"what are the operations"

"how they compose"

"vector spaces on which the action of the group is defined"

rotations, parity, (translations)

scalars, vectors, pseudovectors, ...

Group and Representations

Group \(G\)

• \(\text{identity} \in G\)
• stability \(g h \in G\)
• inverse \(g^{-1} \in G\)

"what are the operations" "how they compose"

"vector spaces on which the action of the group is defined"

Group \(G\)

• \(\text{identity} \in G\)
• stability \(g h \in G\)
• inverse \(g^{-1} \in G\)

Group and Representations

"what are the operations" "how they compose"

"vector spaces on which the action of the group is defined"

Group \(G\)

• \(\text{identity} \in G\)
• stability \(g h \in G\)
• inverse \(g^{-1} \in G\)

Group and Representations

"what are the operations" "how they compose"

"vector spaces on which the action of the group is defined"

Group \(G\)

• \(\text{identity} \in G\)
• stability \(g h \in G\)
• inverse \(g^{-1} \in G\)

Group and Representations

"what are the operations" "how they compose"

"vector spaces on which the action of the group is defined"

Group \(G\)

• \(\text{identity} \in G\)
• stability \(g h \in G\)
• inverse \(g^{-1} \in G\)

Representation \(D(g, x)\)

• \(g\in G\), \(x \in V\)
• Linear \(D(g, x+y) = D(g,x) + D(g,y) \)
• Follow the structure of the group
  \(D(gh,x) = D(g, D(h,x))\)

Group and Representations

"what are the operations" "how they compose"

"vector spaces on which the action of the group is defined"

Group \(G\)

• \(\text{identity} \in G\)
• stability \(g h \in G\)
• inverse \(g^{-1} \in G\)

Representation \(D(g, x)\)

• \(g\in G\), \(x \in V\)
• Linear \(D(g, x+y) = D(g,x) + D(g,y) \)
• Follow the structure of the group
  \(D(gh,x) = D(g, D(h,x))\)

Group and Representations

"what are the operations" "how they compose"

"vector spaces on which the action of the group is defined"

Group \(G\)

• \(\text{identity} \in G\)
• stability \(g h \in G\)
• inverse \(g^{-1} \in G\)

Representation \(D(g, x)\)

• \(g\in G\), \(x \in V\)
• Linear \(D(g, x+y) = D(g,x) + D(g,y) \)
• Follow the structure of the group
  \(D(gh,x) = D(g, D(h,x))\)

Group and Representations

"what are the operations" "how they compose"

"vector spaces on which the action of the group is defined"

Group \(G\)

• \(\text{identity} \in G\)
• stability \(g h \in G\)
• inverse \(g^{-1} \in G\)

Representation \(D(g, x)\)

• \(g\in G\), \(x \in V\)
• Linear \(D(g, x+y) = D(g,x) + D(g,y) \)
• Follow the structure of the group
  \(D(gh,x) = D(g, D(h,x))\)

Group and Representations

"what are the operations" "how they compose"

"vector spaces on which the action of the group is defined"

Group \(G\)

• \(\text{identity} \in G\)
• stability \(g h \in G\)
• inverse \(g^{-1} \in G\)

Representation \(D(g, x)\)

• \(g\in G\), \(x \in V\)
• Linear \(D(g, x+y) = D(g,x) + D(g,y) \)
• Follow the structure of the group
  \(D(gh,x) = D(g, D(h,x))\)

Equivalent notation \(D(g) x\)

• \(D(g) : V\to V\)
• \(D(g) \in \mathbb{R}^{d\times d}\)
• \(D(gh) = D(g) D(h)\)

⚠️ We use this notation in the code

Group and Representations

"what are the operations" "how they compose"

"vector spaces on which the action of the group is defined"

Group \(G\)

• \(\text{identity} \in G\)
• stability \(g h \in G\)
• inverse \(g^{-1} \in G\)

Representation \(D(g, x)\)

• \(g\in G\), \(x \in V\)
• Linear \(D(g, x+y) = D(g,x) + D(g,y) \)
• Follow the structure of the group
  \(D(gh,x) = D(g, D(h,x))\)

Group and Representations

"what are the operations" "how they compose"

"vector spaces on which the action of the group is defined"

Equivalent notation \(D(g) x\)

• \(D(g) : V\to V\)
• \(D(g) \in \mathbb{R}^{d\times d}\)
• \(D(gh) = D(g) D(h)\)

⚠️ We use this notation in the code

Group \(G\)

• \(\text{identity} \in G\)
• stability \(g h \in G\)
• inverse \(g^{-1} \in G\)

Representation \(D(g, x)\)

• \(g\in G\), \(x \in V\)
• Linear \(D(g, x+y) = D(g,x) + D(g,y) \)
• Follow the structure of the group
  \(D(gh,x) = D(g, D(h,x))\)

Group and Representations

"what are the operations" "how they compose"

"vector spaces on which the action of the group is defined"

Equivalent notation \(D(g) x\)

• \(D(g) : V\to V\)
• \(D(g) \in \mathbb{R}^{d\times d}\)
• \(D(gh) = D(g) D(h)\)

⚠️ We use this notation in the code

Group \(G\)

• \(\text{identity} \in G\)
• stability \(g h \in G\)
• inverse \(g^{-1} \in G\)

Representation \(D(g, x)\)

• \(g\in G\), \(x \in V\)
• Linear \(D(g, x+y) = D(g,x) + D(g,y) \)
• Follow the structure of the group
  \(D(gh,x) = D(g, D(h,x))\)

Group and Representations

"what are the operations" "how they compose"

"vector spaces on which the action of the group is defined"

Equivalent notation \(D(g) x\)

• \(D(g) : V\to V\)
• \(D(g) \in \mathbb{R}^{d\times d}\)
• \(D(gh) = D(g) D(h)\)

⚠️ We use this notation in the code

Examples of representations

\(\begin{bmatrix} a^1\\a^2\\a^3\\a^4\\a^5\\a^6\\a^7\\a^8\\a^9\end{bmatrix}\in \mathbb{R}^9\)

Examples of representations

Representations are like data types

It tells you how to interpret the data...

\(\begin{bmatrix} a^1\\a^2\\a^3\\a^4\\a^5\\a^6\\a^7\\a^8\\a^9\end{bmatrix}\in \mathbb{R}^9\)

Examples of representations

Representations are like data types

It tells you how to interpret the data with respect to the \(G\)!

\(\begin{bmatrix} a^1\\a^2\\a^3\\a^4\\a^5\\a^6\\a^7\\a^8\\a^9\end{bmatrix}\in \mathbb{R}^9\)

Examples of representations

Representations are like data types

It tells you how to interpret the data with respect to the \(G\)!

\(\begin{bmatrix} a^1\\a^2\\a^3\\a^4\\a^5\\a^6\\a^7\\a^8\\a^9\end{bmatrix}\in \mathbb{R}^9\)

Knowing that \(a_1, a_2, a_3\) are scalars tells you that they are not affected by a rotation of your system

Examples of representations

\(\begin{bmatrix} a^1\\a^2\\a^3\\a^4\\a^5\\a^6\\a^7\\a^8\\a^9\end{bmatrix}\in \mathbb{R}^9\)

Representations are like data types

It tells you how to interpret the data with respect to the \(G\)!

Examples of representations

\(\begin{bmatrix} a^1\\a^2\\a^3\\a^4\\a^5\\a^6\\a^7\\a^8\\a^9\end{bmatrix}\in \mathbb{R}^9\)

If the system is rotated, the 3 components of the vector change together!

Representations are like data types

It tells you how to interpret the data with respect to the \(G\)!

Examples of representations

\(\begin{bmatrix} a^1\\a^2\\a^3\\a^4\\a^5\\a^6\\a^7\\a^8\\a^9\end{bmatrix}\in \mathbb{R}^9\)

The two vectors transforms indepentently

Representations are like data types

It tells you how to interpret the data with respect to the \(G\)!

Examples of representations

\(\begin{bmatrix} a^1\\a^2\\a^3\\a^4\\a^5\\a^6\\a^7\\a^8\\a^9\end{bmatrix}\in \mathbb{R}^9\)

Representations are like data types

It tells you how to interpret the data with respect to the \(G\)!

system rotated by \(g\)

\(D(g)\begin{bmatrix} a^1\\a^2\\a^3\\a^4\\a^5\\a^6\\a^7\\a^8\\a^9\end{bmatrix}\)

Examples of representations

\(\begin{bmatrix} a^1\\a^2\\a^3\\a^4\\a^5\\a^6\\a^7\\a^8\\a^9\end{bmatrix}\in \mathbb{R}^9\)

Representations are like data types

It tells you how to interpret the data with respect to the \(G\)!

system rotated by \(g\)

\(\begin{bmatrix} a^1\\a^2\\a^3\\a^4\\a^5\\a^6\\a^7\\a^8\\a^9\end{bmatrix}\)

Examples of representations

\(\begin{bmatrix} a^1\\a^2\\a^3\\a^4\\a^5\\a^6\\a^7\\a^8\\a^9\end{bmatrix}\in \mathbb{R}^9\)

Representations are like data types

It tells you how to interpret the data with respect to the \(G\)!

system rotated by \(g\)

\(\begin{bmatrix} a^1\\a^2\\a^3\\a^4\\a^5\\a^6\\a^7\\a^8\\a^9\end{bmatrix}\)

Examples of representations

\(\begin{bmatrix} a^1\\a^2\\a^3\\a^4\\a^5\\a^6\\a^7\\a^8\\a^9\end{bmatrix}\in \mathbb{R}^9\)

Representations are like data types

It tells you how to interpret the data with respect to the \(G\)!

system rotated by \(g\)

\(\begin{bmatrix} a^1\\a^2\\a^3\\a^4\\a^5\\a^6\\a^7\\a^8\\a^9\end{bmatrix}\)

Examples of representations

\(\begin{bmatrix} a^1\\a^2\\a^3\\a^4\\a^5\\a^6\\a^7\\a^8\\a^9\end{bmatrix}\in \mathbb{R}^9\)

Representations are like data types

It tells you how to interpret the data with respect to the \(G\)!

system rotated by \(g\)

\(\begin{bmatrix} a^1\\a^2\\a^3\\a^4\\a^5\\a^6\\a^7\\a^8\\a^9\end{bmatrix}\)

Examples of representations

\(\begin{bmatrix} a^1\\a^2\\a^3\\a^4\\a^5\\a^6\\a^7\\a^8\\a^9\end{bmatrix}\in \mathbb{R}^9\)

system rotated by \(g\)

\(\begin{bmatrix} a^1\\a^2\\a^3\\a^4\\a^5\\a^6\\a^7\\a^8\\a^9\end{bmatrix}\)

e3nn notation:

Examples of representations

\(\begin{bmatrix} a^1\\a^2\\a^3\\a^4\\a^5\\a^6\\a^7\\a^8\\a^9\end{bmatrix}\in \mathbb{R}^9\)

system rotated by \(g\)

\(\begin{bmatrix} a^1\\a^2\\a^3\\a^4\\a^5\\a^6\\a^7\\a^8\\a^9\end{bmatrix}\)

e3nn notation:

Examples of representations

\(\begin{bmatrix} a^1\\a^2\\a^3\\a^4\\a^5\\a^6\\a^7\\a^8\\a^9\end{bmatrix}\in \mathbb{R}^9\)

system rotated by \(g\)

\(\begin{bmatrix} a^1\\a^2\\a^3\\a^4\\a^5\\a^6\\a^7\\a^8\\a^9\end{bmatrix}\)

Examples of representations

\(\begin{bmatrix} a^1\\a^2\\a^3\\a^4\\a^5\\a^6\\a^7\\a^8\\a^9\end{bmatrix}\)

system rotated by \(g\)

\(\begin{bmatrix} a^1\\a^2\\a^3\\a^4\\a^5\\a^6\\a^7\\a^8\\a^9\end{bmatrix}\)

array([[ 1.  ,  0.  ,  0.  ,  0.  ,  0.  ,  0.  ,  0.  ,  0.  ,  0.  ],
       [ 0.  ,  1.  ,  0.  ,  0.  ,  0.  ,  0.  ,  0.  ,  0.  ,  0.  ],
       [ 0.  ,  0.  ,  1.  ,  0.  ,  0.  ,  0.  ,  0.  ,  0.  ,  0.  ],
       [ 0.  ,  0.  ,  0.  ,  0.77,  0.22, -0.6 ,  0.  ,  0.  ,  0.  ],
       [ 0.  ,  0.  ,  0.  , -0.1 ,  0.97,  0.23,  0.  ,  0.  ,  0.  ],
       [ 0.  ,  0.  ,  0.  ,  0.63, -0.12,  0.76,  0.  ,  0.  ,  0.  ],
       [ 0.  ,  0.  ,  0.  ,  0.  ,  0.  ,  0.  ,  0.77,  0.22, -0.6 ],
       [ 0.  ,  0.  ,  0.  ,  0.  ,  0.  ,  0.  , -0.1 ,  0.97,  0.23],
       [ 0.  ,  0.  ,  0.  ,  0.  ,  0.  ,  0.  ,  0.63, -0.12,  0.76]],
      dtype=float32)

Equivariance

\(V\)

\(V'\)

Equivariance

\(V\)

\(V'\)

\(D(g)\)

\(D'(g)\)

\(V\)

\(V'\)

Equivariance

\(V\)

\(V'\)

\(D(g)\)

\(D'(g)\)

\(V\)

\(V'\)

\(f\)

Equivariance

\(V\)

\(V'\)

\(D(g)\)

\(D'(g)\)

\(V\)

\(V'\)

\(f\)

\(f\)

Equivariance

\(V\)

\(V'\)

\(D(g)\)

\(D'(g)\)

\(V\)

\(V'\)

\(f\)

\(f\)

\(f(D(g) x)\)

Equivariance

\(V\)

\(V'\)

\(D(g)\)

\(D'(g)\)

\(V\)

\(V'\)

\(f\)

\(f\)

\(f(D(g) x)\)

\(D'(g) f(x)\)

Equivariance

\(V\)

\(V'\)

\(D(g)\)

\(D'(g)\)

\(V\)

\(V'\)

\(f\)

\(f\)

\(f(D(g) x)\)

\(D'(g) f(x)\)

\(=\)

Polynomials

Most simple yet powerful functions

Polynomials

Most simple yet powerful functions

Be able to create polynomials compatible with rotations is a powerful tool

Polynomials

\(x \mapsto x^2 + 2(x-4)\)

Polynomials

\(x \mapsto x^2 + 2(x-4)\)

\(\begin{bmatrix} x\\ y\\ z \end{bmatrix} \mapsto x^2 + 2(y-z)x\)

Polynomials

\(x \mapsto x^2 + 2(x-4)\)

\(\begin{bmatrix} x\\ y\\ z \end{bmatrix} \mapsto x^2 + 2(y-z)x\)

\(\begin{bmatrix} x\\ y\\ z \end{bmatrix} \mapsto \begin{bmatrix} x^2 + 2(y-z) \\ z^4 + 100 x y z\end{bmatrix}\)

Equivariant Polynomials

\(P(D(g) x) = D'(g) P(x)\)

3 Tools to Make Polynomials

• 🔨Composition \(\circ\)
• 🔧Addition \(+\)
• 🔩Multiplication \(\otimes\)

equivariant 😊

🔨Composition

two equivariant functions

\(f: V_1 \rightarrow V_2\)

\(h: V_2 \rightarrow V_3\)

\(h\circ f\) is equivariant!! 😊

\( h(f(D_1(g) x)) = h(D_2(g) f(x)) = D_3(g) h(f(x)) \)

🔧Addition

two equivariant functions

\(f: V_1 \rightarrow V_3\)

\(h: V_2 \rightarrow V_3\)

\(h + f\) is equivariant!! 😊

\( f(D_1(g) x) + h(D_2(g)x) = D_3(g) (f(x) + h(x)) \)

🔩Multiplication

\(\begin{bmatrix} {\color{red} x_1}\\{\color{red} x_2}\\{\color{red} x_3}\end{bmatrix}\)

\(\begin{bmatrix} {\color{blue} y_1}\\{\color{blue} y_2}\\{\color{blue} y_3}\\{\color{blue} y_4}\\{\color{blue} y_5} \end{bmatrix}\)

transforming with \(D(g)\)

transforming with \(D'(g)\)

\(= \begin{bmatrix} x_1y_1 & x_1y_2 & x_1y_3 & x_1y_4 & x_1y_5 \\ x_2y_1 & x_2y_2 & x_2y_3 & x_2y_4 & x_2y_5 \\ x_3y_1 & x_3y_2 & x_3y_3 & x_3y_4 & x_3y_5 \end{bmatrix}\)

🔩Multiplication

\(\otimes\)

\(= \begin{bmatrix}{\color{red} x_1} {\color{blue} y_1}&{\color{red} x_1} {\color{blue} y_2}&{\color{red} x_1} {\color{blue} y_3}&{\color{red} x_1} {\color{blue} y_4}&{\color{red} x_1} {\color{blue} y_5}\\{\color{red} x_2} {\color{blue} y_1}&{\color{red} x_2} {\color{blue} y_2}&{\color{red} x_2} {\color{blue} y_3}&{\color{red} x_2} {\color{blue} y_4}&{\color{red} x_2} {\color{blue} y_5}\\{\color{red} x_3} {\color{blue} y_1}&{\color{red} x_3} {\color{blue} y_2}&{\color{red} x_3} {\color{blue} y_3}&{\color{red} x_3} {\color{blue} y_4}&{\color{red} x_3} {\color{blue} y_5}\end{bmatrix}\)

Tensor Product

\(\begin{bmatrix} {\color{red} x_1}\\{\color{red} x_2}\\{\color{red} x_3}\end{bmatrix}\)

\(\begin{bmatrix} {\color{blue} y_1}\\{\color{blue} y_2}\\{\color{blue} y_3}\\{\color{blue} y_4}\\{\color{blue} y_5} \end{bmatrix}\)

\(\text{vector} \otimes \text{vector} \otimes \text{vector} \otimes \dots\)

tensors of shape \(3\times3\times3\times\dots\)

Cartesian Tensors

Reducible representations

\(D\) defined on \(V\)

is reducible if

\(\exists W \subset V\)

such that

\(D|_W\) is a representation

Reducible representations

Famous Example

\(\begin{bmatrix}{\color{red} x_1} {\color{blue} x_2}&{\color{red} x_1} {\color{blue} y_2}&{\color{red} x_1} {\color{blue} z_2}\\{\color{red} y_1} {\color{blue} x_2}&{\color{red} y_1} {\color{blue} y_2}&{\color{red} y_1} {\color{blue} z_2}\\{\color{red} z_1} {\color{blue} x_2}&{\color{red} z_1} {\color{blue} y_2}&{\color{red} z_1} {\color{blue} z_2}\end{bmatrix}\)

\(D\) defined on \(V\)

is reducible if

\(\exists W \subset V\)

such that

\(D|_W\) is a representation

\(\begin{bmatrix} {\color{red} x_1}\\{\color{red} y_1}\\{\color{red} z_1}\end{bmatrix}\otimes\begin{bmatrix} {\color{blue} x_2}\\{\color{blue} y_2}\\{\color{blue} z_2}\end{bmatrix} = \)

Reducible representations

\(\begin{bmatrix}{\color{red} x_1} {\color{blue} x_2}&{\color{red} x_1} {\color{blue} y_2}&{\color{red} x_1} {\color{blue} z_2}\\{\color{red} y_1} {\color{blue} x_2}&{\color{red} y_1} {\color{blue} y_2}&{\color{red} y_1} {\color{blue} z_2}\\{\color{red} z_1} {\color{blue} x_2}&{\color{red} z_1} {\color{blue} y_2}&{\color{red} z_1} {\color{blue} z_2}\end{bmatrix}\)

\(D\) is reducible if

\(\exists W \subset V\)

such that

\(D|_W\) is a representation

Irreducible representations

For the group of rotations (\(SO(3)\))

They are index by \(L=0, 1, 2, \dots\)

Of dimension \(2L+1\)

Irreducible representations

For the group of rotations + parity (\(O(3)\))

They are index by \(L=0, 1, 2, \dots\)

Of dimension \(2L+1\)

Even

Odd

🔩Multiplication

\(L_1 \otimes L_2 = |L_1-L_2| \oplus \dots \oplus (L_1+L_2)\)

• \( 2 \otimes 1 = 1 \oplus 2 \oplus 3 \)
• \( 2 \otimes 2 = 0\oplus 1 \oplus 2 \oplus 3 \oplus 4 \)

🔨Composition

🔧Addition

🔩Multiplication

Composition of equivariant polynomials ✅

Addition of equivariant polynomials ✅

Tensor Product of equivariant polynomials ✅

 \(L_1 \otimes L_2 = |L_1-L_2| \oplus \dots \oplus (L_1+L_2)\) 

🔨Composition

🔧Addition

🔩Multiplication

Composition of equivariant polynomials ✅

Addition of equivariant polynomials ✅

Tensor Product of equivariant polynomials ✅

 \(L_1 \otimes L_2 = |L_1-L_2| \oplus \dots \oplus (L_1+L_2)\) 

Spherical Harmonics

Representation of highest order (\(l\)) in \(\vec x \otimes \vec x \otimes \dots\)

https://e3nn.org/mrs

Tensor Product with weights

\(3\times3=1+3+5\)

\(\begin{bmatrix}{\color{red} x_1} {\color{blue} x_2}&{\color{red} x_1} {\color{blue} y_2}&{\color{red} x_1} {\color{blue} z_2}\\{\color{red} y_1} {\color{blue} x_2}&{\color{red} y_1} {\color{blue} y_2}&{\color{red} y_1} {\color{blue} z_2}\\{\color{red} z_1} {\color{blue} x_2}&{\color{red} z_1} {\color{blue} y_2}&{\color{red} z_1} {\color{blue} z_2}\end{bmatrix}\)

\({\color{red}x_1}{\color{blue}x_2} + {\color{red}y_1}{\color{blue}y_2} + {\color{red}z_1} {\color{blue}z_2}\)

\(\begin{bmatrix}{\color{red}y_1}{\color{blue}z_2}-{\color{red}z_1} {\color{blue}y_2}\\ {\color{red}z_1}{\color{blue}x_2}-{\color{red}x_1}{\color{blue}z_2}\\ {\color{red}x_1}{\color{blue}y_2}-{\color{red}y_1}{\color{blue}x_2}\end{bmatrix}\)

\(\begin{bmatrix}c ( {\color{red}x_1} {\color{blue}z_2} + {\color{red}z_1} {\color{blue}x_2} ) \\ c ( {\color{red}x_1} {\color{blue}y_2} + {\color{red}y_1} {\color{blue}x_2} ) \\ 2 {\color{red}y_1} {\color{blue}y_2} - {\color{red}x_1} {\color{blue}x_2} - {\color{red}z_1} {\color{blue}z_2} \\ c ( {\color{red}y_1} {\color{blue}z_2} + {\color{red}z_1} {\color{blue}y_2} ) \\ c ( {\color{red}z_1} {\color{blue}z_2} - {\color{red}x_1} {\color{blue}x_2} ) \\\end{bmatrix}\)

\(\begin{bmatrix} {\color{red} x_1}\\{\color{red} y_1}\\{\color{red} z_1}\end{bmatrix}\otimes\begin{bmatrix} {\color{blue} x_2}\\{\color{blue} y_2}\\{\color{blue} z_2}\end{bmatrix} = \)

"1o" time "1o"

"1o"

"1o"

"0e"

"1e"

"2e"

https://e3nn.org/mrs

Tensor Product with weights

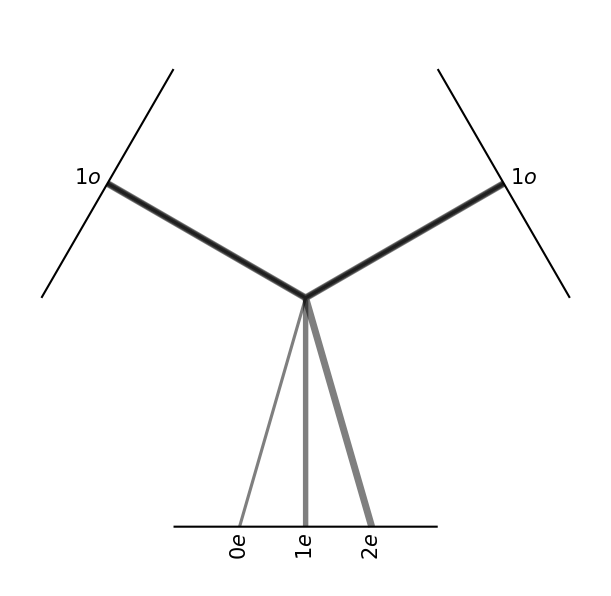
first argument

second argument

output

\(3\times3=1+3+5\)

https://e3nn.org/mrs

Tensor Product with weights

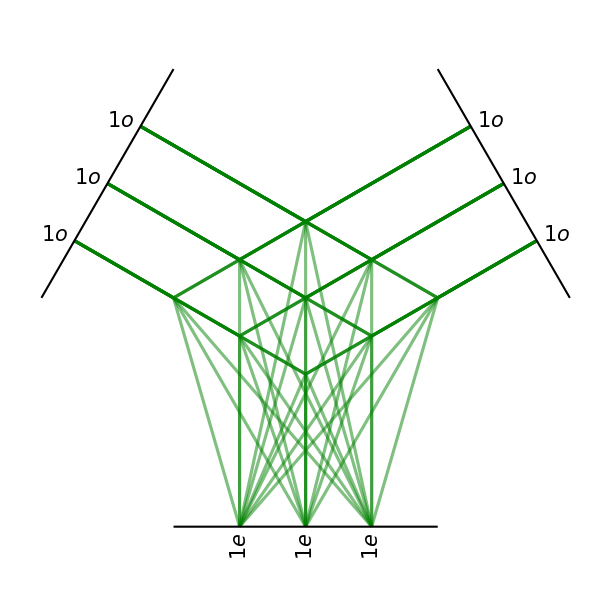
3 vectors times 3 vectors given 3 pseudovectors

each output is the weight sum of 9 pseudovectors

This operation contains 27 parameters

https://e3nn.org/mrs

Reduce Tensor Product

Consider for instance the inertia tensor

\(\displaystyle I_{ij} = \int dx \; \rho(x) \; (\|x\|^2 \delta_{ij} - x_i x_j)\)

https://e3nn.org/mrs

Nonlinearities

Nonlinearities

Gate

\( \phi(P(x)) Q(x) \)

Conclusion

• Group and representations
• 😊 Equivariance \(f({\color{purple}D(g)} x) = {\color{darkgreen}D'(g)} f(x)\)
  • 🔨Composition
  • 🔧Addition
• Polynomials
  •  🔩 Tensor Product  \(L_1 \otimes L_2 = |L_1-L_2| \oplus \dots \oplus (L_1+L_2)\)
  • Polynomials with weights
• ​Nonlinearities
  • ​Gate

https://e3nn.org/mrs

Thank you for listening!

https://e3nn.org/mrs