Generalization
Setup
- binary classification
- quadratic hinge loss
- constant width : h
- L hidden layers
- relu
\mathcal{L} = \frac{1}{P} \sum_{\mu=1}^P \theta(1 - f_\mu y_\mu) \frac12 (\underbrace{1 - f_\mu y_\mu}_{\Delta_\mu})^2
here d=3, h=5 and L=3
Setup: Initialization
weights = orthogonal
bias = 0
Deep Information Propagation
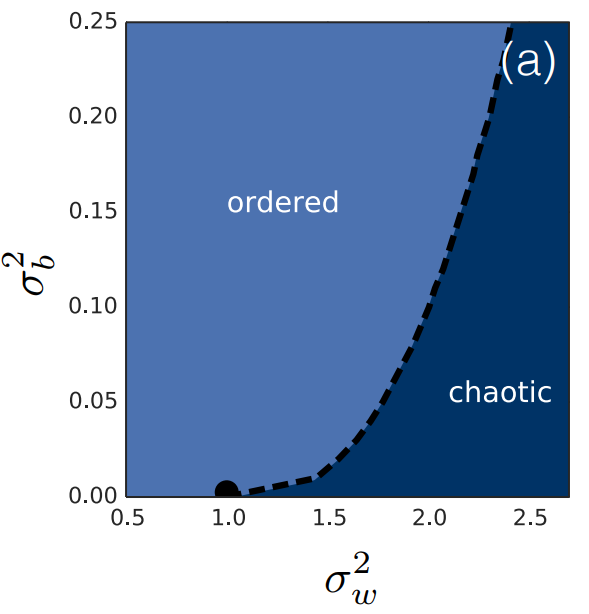
But this is for tanh !!!!
Setup: Optimization
\lambda = 0.1 / h^{1.5}
ADAM
Neural Tangent Kernel
https://arxiv.org/abs/1806.07572
full batch
MNIST
x, y = get_mnist()
m = x.mean(0)
cov = (x - m).t() @ (x - m) / len(x)
e, v = cov.symeig(eigenvectors=True)
x = (x - m) @ v[:, :30] / e[:30].sqrt() # PCA
y = y % 2 # parity- 30 component of PCA
- labels = parity
L=5
P=10k : number of data points
N : number of parameters
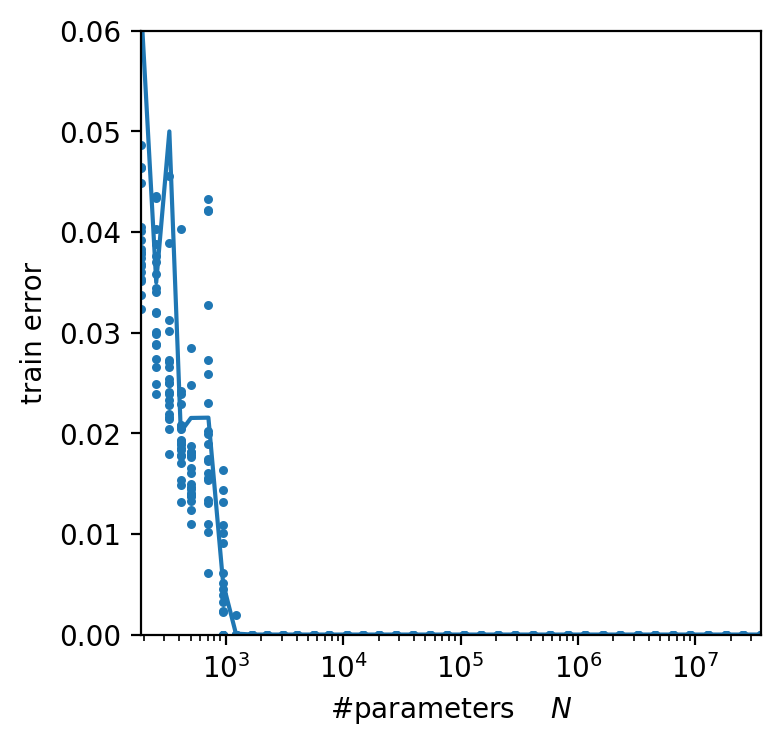
r = \frac{P}{N} \simeq \frac{10}{1.2} \simeq 8
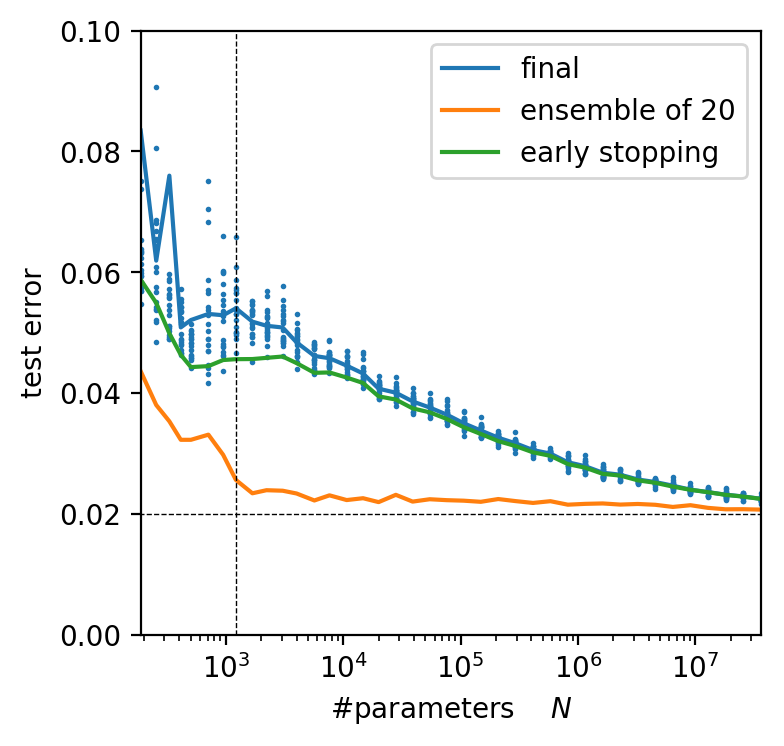
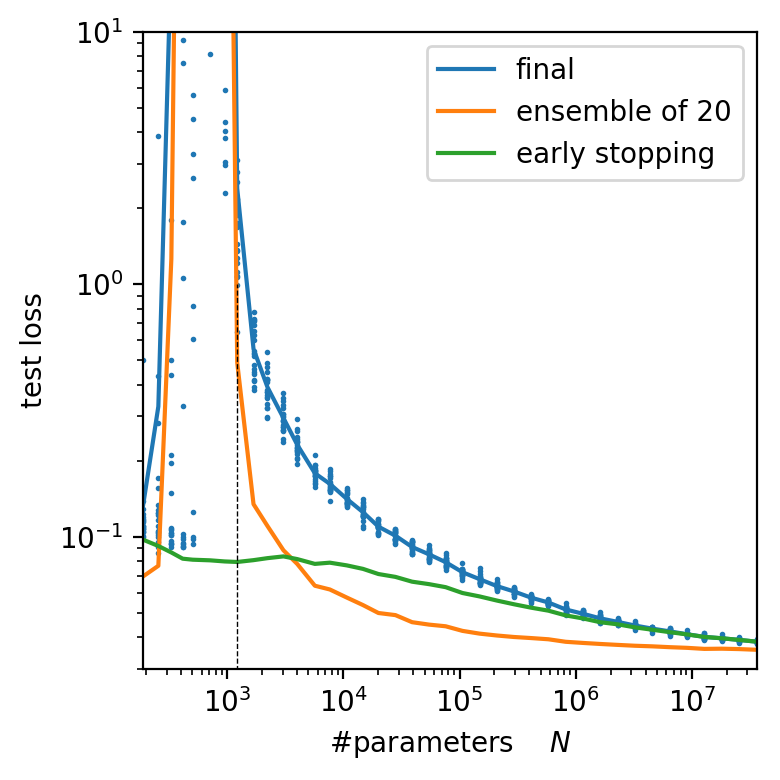
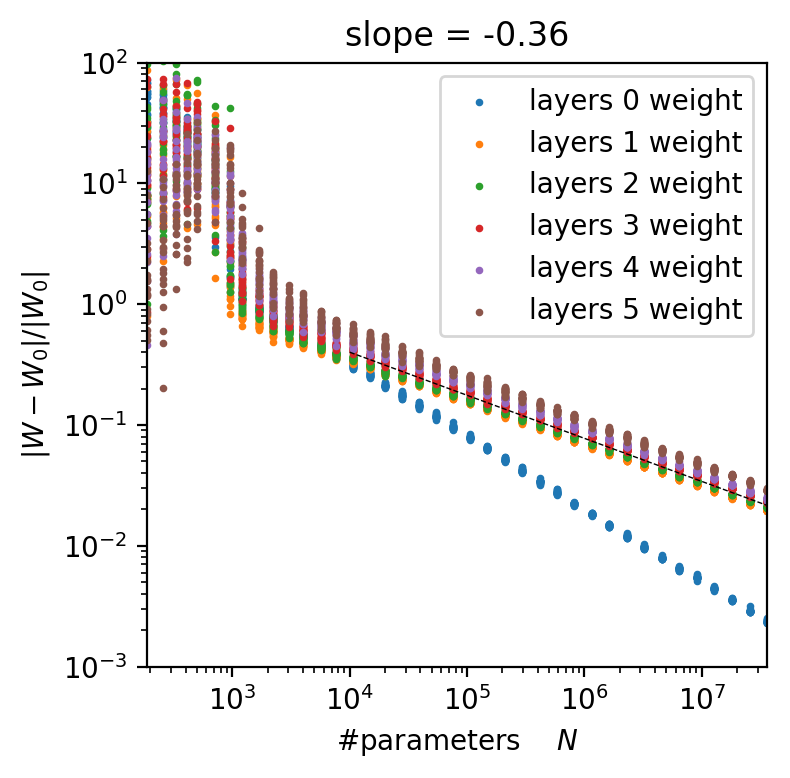
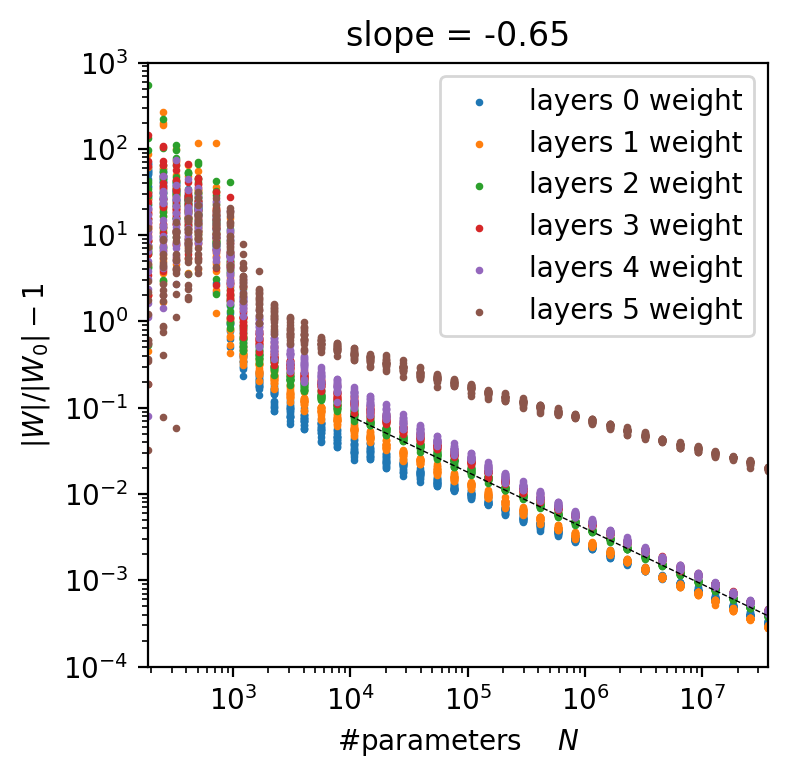
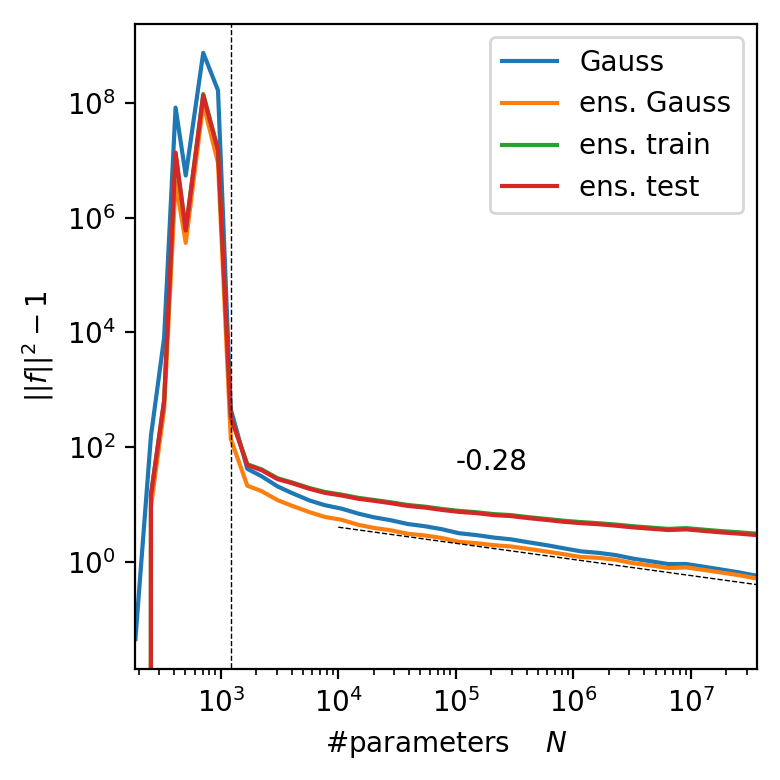
\langle f, g \rangle = \int d\mu(x) f(x) g(x)
||f||^2 = \int d\mu(x) f(x)^2
P=10k
L=5
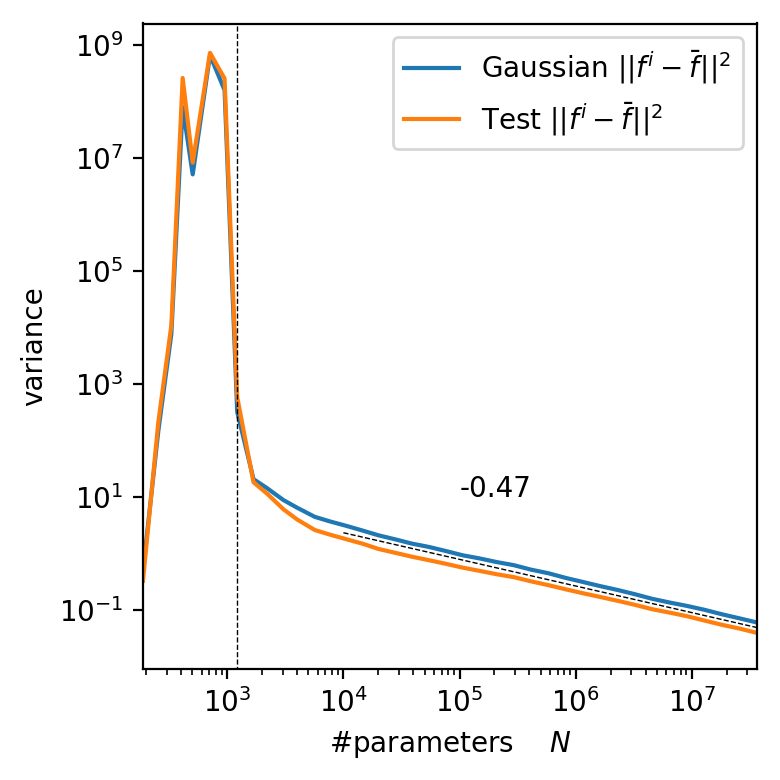
\langle f, g \rangle = \int d\mu(x) f(x) g(x)
\mathbb{V} f = \mathbb{E} || f - \mathbb{E} f ||^2
P=10k
L=5
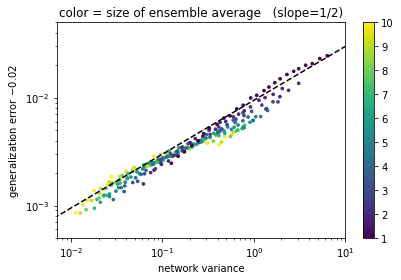
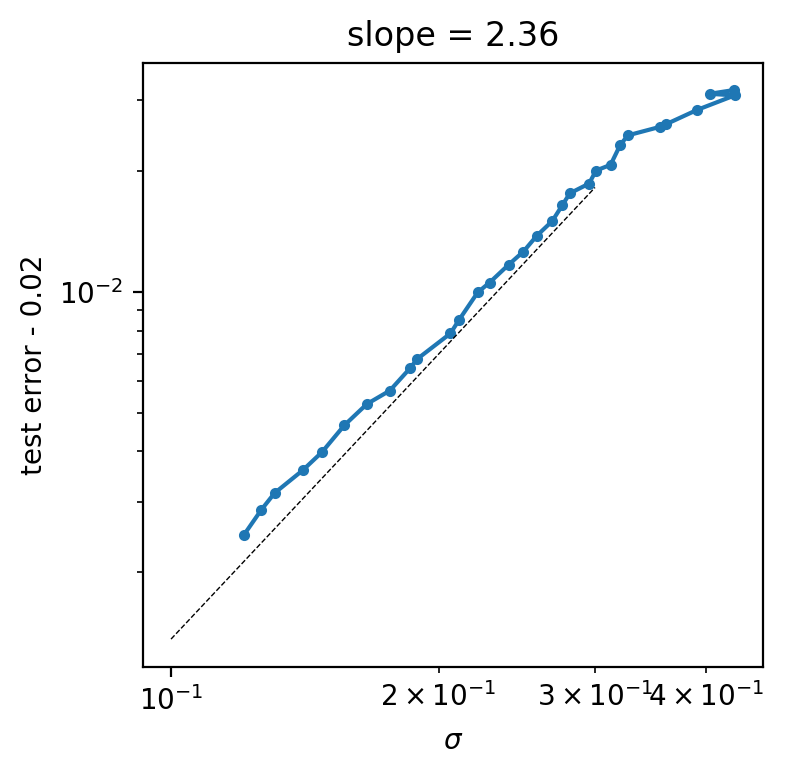
\epsilon - \epsilon^* \sim \sqrt{\mathbb V}
at blackboard :
idea variance <--> generalization
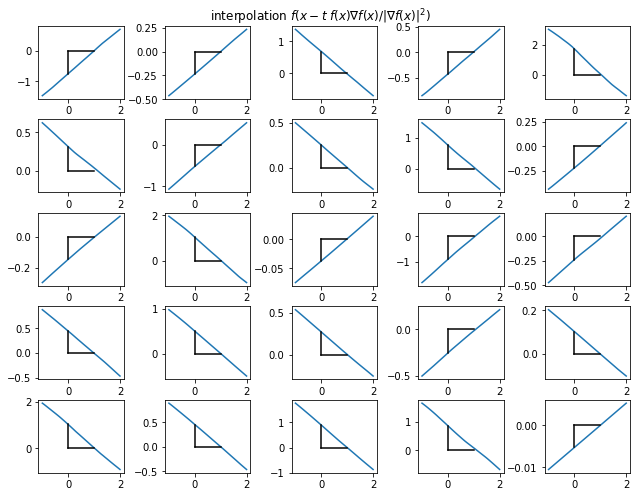
\sigma \simeq \frac{|f(x)|}{||\nabla f(x)||}
for x in testset
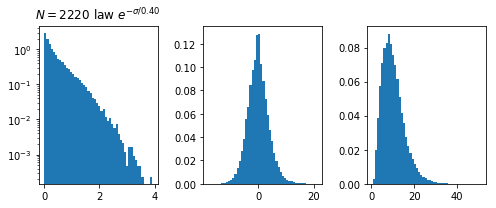
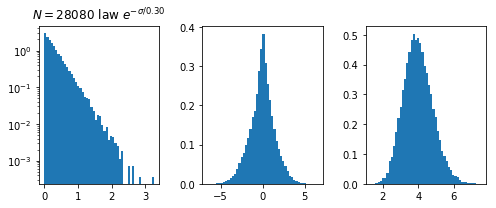
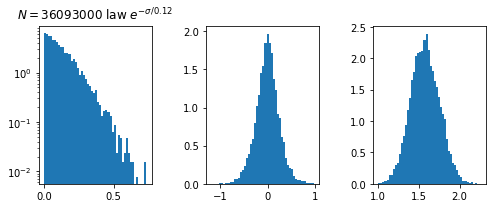
f(x)
||\nabla f(x)||
\sigma
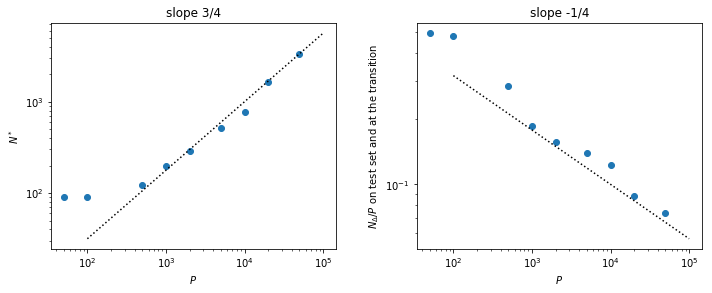
N*(P)
Open questions
- Does really the variance vanish for large N ?
- Does these results extend to CNN ?
- relation between N*(P) and data complexity
- robustness & stability (adversarial vulnerability)
- Speed of vonvergence of
\lim_{P\to \infty} \lim_{N\to \infty} \epsilon(P,N) = 0
Generalization
By Mario Geiger
