Loss landscape and symmetries in Neural Networks
Mario Geiger
Professor: Matthieu Wyart
Physics of Complex Systems Laboratory

...now postdoc in MIT
with
Prof Tess Smidt
Paradoxes of deep learning
Landscape vs Parameterization
Data Symmetries
Table of contents
Introduction to deep learning
Color code
Questions
Open problems

model
\(\displaystyle w\in \mathbb{R}^N\)
Classification with deep learning
Classification with deep learning

dataset
\(\displaystyle w\in \mathbb{R}^N\)

\(\displaystyle \mathcal{L} = \frac1P \sum_{i=1}^{P} \ell(f(w, x_i),y_i)\)
loss function
\(\displaystyle w\in \mathbb{R}^N\)
Classification with deep learning

\(\displaystyle \mathcal{L} = \frac1P \sum_i \ell(f(w, x_i),y_i)\)
gradient descent
\(\displaystyle w\in \mathbb{R}^N\)
Classification with deep learning
\( w^{t+1} = w^t - \nabla_w \mathcal{L}(w^t) \)
\(\displaystyle P\)
\(\displaystyle N\)
Classification with deep learning
number of parameters
number of training samples
In this talk I will use the following notation
Paradoxes
Landscape vs Parameterization
Data Symmetries
Non-convex \(\mathcal{L}\)
Overparameterization
Curse of dimensionality

- No guarantees to be convex
- High dimensional space (\(N\))
Why not stuck in a local minima?
- Over parameterized: \(\mathcal{L} \to 0\)
- \(\mathcal{L}\) connected at the bottom
Freeman and Bruna (2017)
Soudry and Carmon (2016)
Cooper (2018)
- \(\mathcal{L}\) connected at the bottom
- Under Parametrized: \(\mathcal{L}\) glassy
Baity-Jesi et al. (2018)
How is the transition between under and over parameterized regimes?

Paradoxes
Landscape vs Parameterization
Data Symmetries
Non-convex \(\mathcal{L}\)
Overparameterization
Curse of dimensionality

- State of the art neural networks \( P \ll N\)
: test/generalization error
= number of parameters
Neyshabur et al. (2017, 2018); Bansal et al. (2018); Advani et al. (2020)
Why does the test error decreases with \(N\)?
Paradoxes
Landscape vs Parameterization
Data Symmetries
Non-convex \(\mathcal{L}\)
Overparameterization
Curse of dimensionality

\(P =\) size of trainset
\(\delta =\) distance to closest neighbor
Bach (2017)
Paradoxes
Landscape vs Parameterization
Data Symmetries
Non-convex \(\mathcal{L}\)
Overparameterization
Curse of dimensionality

Hestness et al. (2017)
regression + Lipschitz continuous
Luxburg and Bousquet (2004)
Paradoxes
Landscape vs Parameterization
Data Symmetries
Non-convex \(\mathcal{L}\)
Overparameterization
Curse of dimensionality
- Kernel Method:
sample complexity /= #{ invariant transformations }
Bietti et al. (2021)
- Convolutional Neural Network (CNN) are invariant under translations

sample complexity = \(P\) required to get \(\epsilon\)
Paradoxes
Landscape vs Parameterization
Data Symmetries
Non-convex \(\mathcal{L}\)
Overparameterization
Curse of dimensionality
Figure from (Geometric Deep Learning by Bronstein, Bruna, Cohen and Veličković)
- Translations are a small set in the space of image transformations
- Labels are invariant to smooth deformations or diffeomorphisms of small magnitude
Bruna and Mallat (2013); Mallat (2016)
Paradoxes
Landscape vs Parameterization
Data Symmetries
Non-convex \(\mathcal{L}\)
Overparameterization
Curse of dimensionality
Is stability to diffeomorphisms responsible for beating the curse of dimensionality?
- Recent empirical results revealed that small shifts of images can change the output a lot
Azulay and Weiss (2018); Dieleman et al. (2016); Zhang (2019)
Paradoxes
Landscape vs Parameterization
Data Symmetries
Non-convex \(\mathcal{L}\)
Overparameterization
Curse of dimensionality
Empirical evidence?
Can we generalize CNN invariance to other symmetries?
- CNNs perform much better than Fully-Connected networks
- Many tasks involve symmetries like rotation or mirror
Paradoxes
Landscape vs Parameterization
Data Symmetries
Non-convex \(\mathcal{L}\)
Overparameterization
Curse of dimensionality
Landscape vs Parameterization
Data Symmetries
Jamming
Double descent
Phase Diagram
Paradoxes
How is the transition between under and over parameterized regimes?
The same question was asked in the physics of glasses
Landscape vs Parameterization
Data Symmetries
Jamming
Double descent
Phase Diagram
Paradoxes
\(\displaystyle U = \sum_{ij} U_{ij}\)
Van der Waals
Landscape vs Parameterization
Data Symmetries
Jamming
Double descent
Phase Diagram
Paradoxes
\(\displaystyle U = \sum_{ij} U_{ij}\)
Van der Waals
Finite range interaction
Landscape vs Parameterization
Data Symmetries
Jamming
Double descent
Phase Diagram
Paradoxes
\(\displaystyle U = \sum_{ij} U_{ij}\)
Van der Waals
Finite range interaction
SAT/UNSAT problem
num. of constraints \(N_\Delta\)
Landscape vs Parameterization
Data Symmetries
Jamming
Double descent
Phase Diagram
Paradoxes
\(\displaystyle U = \sum_{ij} U_{ij}\)
Van der Waals
Finite range interaction
SAT/UNSAT problem
num. of constraints \(N_\Delta\)
Sharp Transition:
Jamming
Landscape vs Parameterization
Data Symmetries
Jamming
Double descent
Phase Diagram
Paradoxes

Low density: flat directions
\(N_\Delta = 0\)
Landscape vs Parameterization
Data Symmetries
Jamming
Double descent
Phase Diagram
Paradoxes

Low density: flat directions

High density: glassy
\(N_\Delta = 0\)
\(N_\Delta \geq N\)
Landscape vs Parameterization
Data Symmetries
Jamming
Double descent
Phase Diagram
Paradoxes

Low density: flat directions
High density: glassy

\(N_\Delta=N\)
Sharp jamming transition
Landscape vs Parameterization
Data Symmetries
Jamming
Double descent
Phase Diagram
Paradoxes

Low density: flat directions
High density: glassy



\(N_\Delta < N\) \(N_\Delta=N\)
Sharp jamming transition
Landscape vs Parameterization
Data Symmetries
Jamming
Double descent
Phase Diagram
Paradoxes

Low density: flat directions
High density: glassy



\(N_\Delta < N\) \(N_\Delta=N\)
Sharp jamming transition
Prediction for Neural Networks
Landscape vs Parameterization
Data Symmetries
Jamming
Double descent
Phase Diagram
cross entropy loss (long range)

Paradoxes
Landscape vs Parameterization
Data Symmetries
Jamming
Double descent
Phase Diagram
cross entropy loss
(long range)

Paradoxes
quadratic hinge loss
(finite range)

Landscape vs Parameterization
Data Symmetries
Jamming
Double descent
Phase Diagram
| Particles | Neural Networks |
|---|---|
| energy | loss |
| overlapping particles | point below margin |
| density | trainset size / parameters = P/N |
Paradoxes

margin
Landscape vs Parameterization
Data Symmetries
Jamming
Double descent
Phase Diagram

Fully Connected 5 hidden layers relu, ADAM MNIST (pca d=10)
Geiger, M., Spigler, S., d’Ascoli, S., Sagun, L., Baity-Jesi, M., Biroli, G., and Wyart, M. (2019)
Paradoxes
Landscape vs Parameterization
Data Symmetries
Jamming
Double descent
Phase Diagram
Fully Connected 5 hidden layers relu, ADAM MNIST (pca d=10)
Geiger, M., Spigler, S., d’Ascoli, S., Sagun, L., Baity-Jesi, M., Biroli, G., and Wyart, M. (2019)
Paradoxes

Landscape vs Parameterization
Data Symmetries
Jamming
Double descent
Phase Diagram
Fully Connected 5 hidden layers relu, ADAM MNIST (pca d=10)
Geiger, M., Spigler, S., d’Ascoli, S., Sagun, L., Baity-Jesi, M., Biroli, G., and Wyart, M. (2019)
Paradoxes

Landscape vs Parameterization
Data Symmetries
Jamming
Double descent
Phase Diagram
There is sharp jamming transition, in the same universality class as ellipses
Paradoxes
How is the transition between under and over parameterized?
Landscape vs Parameterization
Data Symmetries
Jamming
Double descent
Phase Diagram
There is sharp jamming transition, in the same universality class as ellipses
Paradoxes
How is the transition between under and over parameterized?
Why not stuck in a local minima?
Crank-up the number of parameters and you are not stuck
Landscape vs Parameterization
Data Symmetries
Jamming
Double descent
Phase Diagram
There is sharp jamming transition, in the same universality class as ellipses
Paradoxes
How is the transition between under and over parameterized?
Why not stuck in a local minima?
Crank-up the number of parameters and you are not stuck
What about overfitting?
Landscape vs Parameterization
Data Symmetries
Jamming
Double descent
Phase Diagram
Paradoxes
Double Descent
Why does the test error decreases with \(N\)?
Landscape vs Parameterization
Data Symmetries
Jamming
Double descent
Phase Diagram

P=5000 Fully Connected 2 hidden layers swish
softhinge MNIST (pca d=10)
Paradoxes

Landscape vs Parameterization
Data Symmetries
Jamming
Double descent
Phase Diagram

P=5000 Fully Connected 2 hidden layers swish
softhinge MNIST (pca d=10)
Paradoxes

Landscape vs Parameterization
Data Symmetries
Jamming
Double descent
Phase Diagram

P=5000 Fully Connected 2 hidden layers swish
softhinge MNIST (pca d=10)
Paradoxes
Jamming
Cusp at jamming?
Landscape vs Parameterization
Data Symmetries
Jamming
Double descent
Phase Diagram

P=5000 Fully Connected 2 hidden layers swish
softhinge MNIST (pca d=10)
Paradoxes
Jamming
Cusp at jamming?
Slow decrease?
Landscape vs Parameterization
Data Symmetries
Jamming
Double descent
Phase Diagram
Paradoxes
Cusp at jamming?
Slow decrease?
We show that the predictor explode at jamming, we predict the exponent
Mario Geiger et al J. Stat. Mech. (2020) 023401
Need to understand what happens at \(N\to \infty\)
Landscape vs Parameterization
Data Symmetries
Jamming
Double descent
Phase Diagram
Neural Tangent Kernel
Space of functions \(X\to Y\)
Paradoxes
Arthur Jacot et al. Neurips (2018)
Landscape vs Parameterization
Data Symmetries
Jamming
Double descent
Phase Diagram
Neural Tangent Kernel
Manifold \(f:W\to (X\to Y)\)
Paradoxes

Space of functions \(X\to Y\)
\(f(w_0)\)
Arthur Jacot et al. Neurips (2018)
(curry notation)
Landscape vs Parameterization
Data Symmetries
Jamming
Double descent
Phase Diagram
Neural Tangent Kernel
Paradoxes

Space of functions \(X\to Y\)

Manifold \(f:W\to (X\to Y)\)
tangent space
In the limit \(N\to\infty\), parameters change only a little.
Arthur Jacot et al. Neurips (2018)
\(f(w_0)\)
Landscape vs Parameterization
Data Symmetries
Jamming
Double descent
Phase Diagram
Neural Tangent Kernel
Paradoxes


Manifold \(f:W\to (X\to Y)\)
\(\displaystyle \Theta(w, x_1, x_2) = \nabla_w f(w,x_1) \cdot \nabla_w f(w, x_2)\)
tangent space
Arthur Jacot et al. Neurips (2018)
\(f(w_0)\)
Landscape vs Parameterization
Data Symmetries
Jamming
Double descent
Phase Diagram
Neural Tangent Kernel
Paradoxes

Manifold \(f:W\to (X\to Y)\)

\(\displaystyle \frac{d}{dt}f(w, \cdot) \propto \ell_i' \Theta(w, x_i, \cdot)\)
Arthur Jacot et al. Neurips (2018)
\(\displaystyle \Theta(w, x_1, x_2) = \nabla_w f(w,x_1) \cdot \nabla_w f(w, x_2)\)
Landscape vs Parameterization
Data Symmetries
Jamming
Double descent
Phase Diagram
Neural Tangent Kernel
Paradoxes

Manifold \(f:W\to (X\to Y)\)

\(\displaystyle \frac{d}{dt}f(w, \cdot) \propto \ell_i' \Theta(w, x_i, \cdot)\)
Arthur Jacot et al. Neurips (2018)
Well defined behavior at \(N=\infty\)
\(\displaystyle \Theta(w, x_1, x_2) = \nabla_w f(w,x_1) \cdot \nabla_w f(w, x_2)\)
Landscape vs Parameterization
Data Symmetries
Jamming
Double descent
Phase Diagram
- \(\| \Theta - \langle \Theta \rangle \|^2 \sim N^{-1/2}\)
- \(\Rightarrow \mathrm{Var}(f) \sim N^{-1/2}\)
- \(\Rightarrow \epsilon(N) - \epsilon_\infty \sim N^{-1/2}\)
Mario Geiger et al J. Stat. Mech. (2020) 023401
Paradoxes
Noisy convergence toward a well defined dynamics
Why does the test error decreases with \(N\)?
Landscape vs Parameterization
Data Symmetries
Jamming
Double descent
Phase Diagram
- \(\| \Theta - \langle \Theta \rangle \|^2 \sim N^{-1/2}\)
- \(\Rightarrow \mathrm{Var}(f) \sim N^{-1/2}\)
- \(\Rightarrow \epsilon(N) - \epsilon_\infty \sim N^{-1/2}\)
Mario Geiger et al J. Stat. Mech. (2020) 023401
Paradoxes
Noisy convergence toward a well defined dynamics
Why does the test error decreases with \(N\)?
Can we remove these fluctuations without sending \(N\) to \(\infty\)?
Landscape vs Parameterization
Data Symmetries
Jamming
Double descent
Phase Diagram
Paradoxes

Ensemble average
Generalization error of the average of 20 network's outputs
\(\sim N^{-1/2}\)
Landscape vs Parameterization
Data Symmetries
Jamming
Double descent
Phase Diagram
Paradoxes
Noisy convergence toward a well defined dynamics...
...described by the NTK in which the weights do not move!
no feature learning?
Neural network do learn features
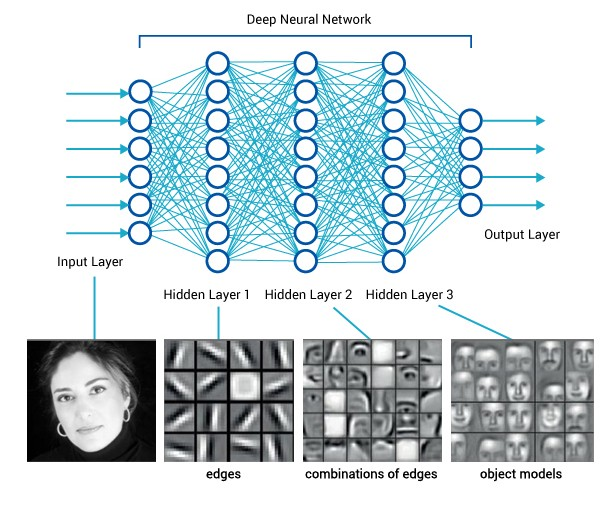
Le Quoc V. IEEE (2013)
Landscape vs Parameterization
Data Symmetries
Jamming
Double descent
Phase Diagram
Paradoxes
Mean-Field limit
Mei et al. (2018); Rotskoff and Vanden-Eijnden (2018); Chizat and Bach (2018); Sirignano and Spiliopoulos (2020b); Mei et al. (2019); Nguyen (2019); Sirignano and Spiliopoulos (2020a), with recent development for deeper nets, see e.g. Nguyen and Pham (2020)
Another limit, different than NTK in which the neural network can learn features
Landscape vs Parameterization
Data Symmetries
Jamming
Double descent
Phase Diagram
Paradoxes
NTK vs. Mean-Field
Q1 How to quantify if the network is rather Mean-Field or NTK?
Q2 Which of the two limits perform better?
Landscape vs Parameterization
Data Symmetries
Jamming
Double descent
Phase Diagram
\(f(w, x) = \frac1{\sqrt{h}} w^{L+1} \phi(\frac1{\sqrt{h}} \dots)\)
Paradoxes
NTK Mean-Field
\(f(w, x) = \frac1h w^{L+1} \phi(\frac1{\sqrt{h}} \dots)\)
Landscape vs Parameterization
Data Symmetries
Jamming
Double descent
Phase Diagram
\(f(w, x) = \frac1{\sqrt{h}} w^{L+1} \phi(\frac1{\sqrt{h}} \dots)\)
Paradoxes
\(\tilde f(w, x) = \frac1h w^{L+1} \phi(\frac1{\sqrt{h}} \dots)\)
\(\tilde\alpha (\tilde f(w, x) - \tilde f(w_0, x))\)
(linearize to allow small weights change to have an impact)
Chizat et al. Neurips (2019)
Landscape vs Parameterization
Data Symmetries
Jamming
Double descent
Phase Diagram

Paradoxes
Q1 How to quantify if the network is rather Mean-Field or NTK?
\(\Delta\Theta \equiv \Theta(w) - \Theta(w_0)\)
level sets delimits a smooth transition
NTK
Mean-Field
Landscape vs Parameterization
Data Symmetries
Jamming
Double descent
Phase Diagram


Paradoxes
- Double descent is also present in feature learning
Landscape vs Parameterization
Data Symmetries
Jamming
Double descent
Phase Diagram

Fully Connected 2 hidden layers
Paradoxes
= number of neurons per layer
Q2 Which of the two limits perform better?
gradient flow
FC: lazy > feature
CNN: feature > lazy
Mario Geiger et al J. Stat. Mech. (2020) 113301
Mario Geiger et al Physics Reports V924 (2021)
Open problem: Not well understood which regime performs better
Lee Jaehoon et al. (2020)
Landscape vs Parameterization
Data Symmetries
Jamming
Double descent
Phase Diagram
Paradoxes
Bonus: Phase Diagram of SGD
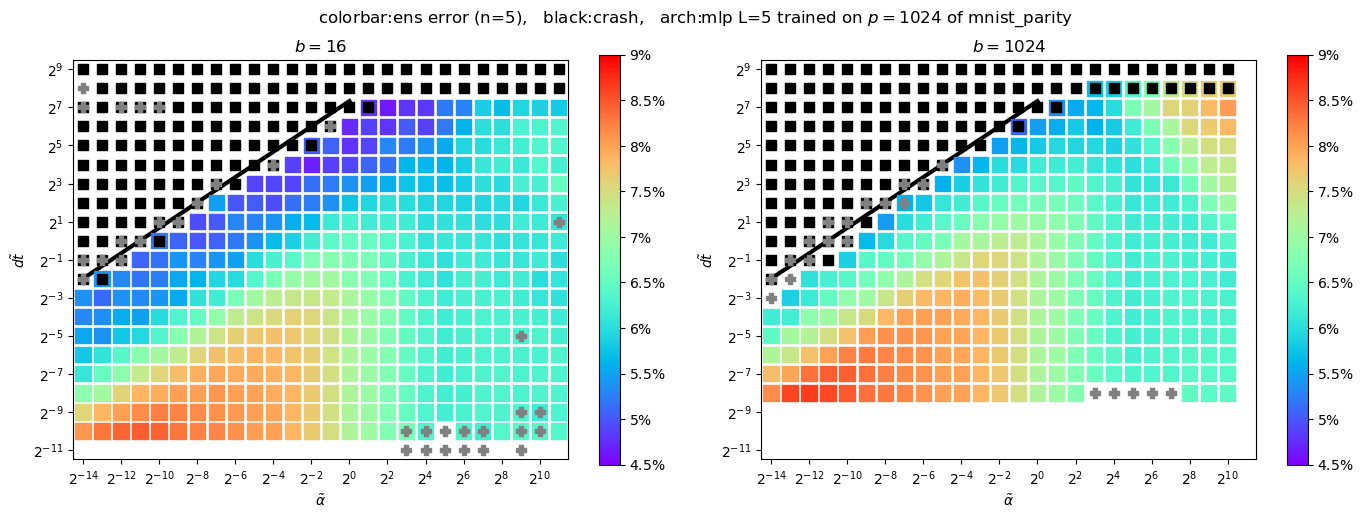
Fully connected
MNIST
P=1024
Landscape vs Parameterization
Data Symmetries
Jamming
Double descent
Phase Diagram
Paradoxes
Bonus: Phase Diagram of SGD

Landscape vs Parameterization
Data Symmetries
Paradoxes
- Why not stuck in a local minima?
- How is the transition between under/over parameterized?
- Why does the test error decreases with \(N\)?
- Q1 How to quantify if the network is rather Mean-Field or NTK?
- Q2 Which of the two limits perform better?
- Crank-up \(N\)
-
There is sharp jamming transition, in the same universality class as ellipses
- Noisy convergence toward a well defined dynamics
-
Change in NTK delimits a smooth transition controlled by \(\tilde\alpha\)
-
FC: lazy > feature
CNN: feature > lazy
still an open problem
Landscape vs Parameterization
Data Symmetries
Data Symmetries
Curse of dimensionality not answered so far
One needs to take into account the structure of the data.
Data contains symmetries
Paradoxes
Landscape vs Parameterization
Data Symmetries
Diffeomorphisms
Euclidean Neural Network
Paradoxes
Is stability to diffeomorphisms responsible for beating the curse of dimensionality?
Aim: measure the stability toward diffeomorphisms
Landscape vs Parameterization
Data Symmetries
Diffeomorphisms
Maximum entropy distribution
Euclidean Neural Network
Paradoxes

diffeomorphisms are controlled by a temperature parameter
Landscape vs Parameterization
Data Symmetries
Diffeomorphisms
Maximum entropy distribution
Euclidean Neural Network
Paradoxes

diffeomorphisms are controlled by a temperature parameter
Landscape vs Parameterization
Data Symmetries
Diffeomorphisms
Maximum entropy distribution
Euclidean Neural Network
Paradoxes

diffeomorphisms are controlled by a temperature parameter
Landscape vs Parameterization
Data Symmetries
Diffeomorphisms
Maximum entropy distribution
Euclidean Neural Network
Paradoxes

diffeomorphisms are controlled by a temperature parameter
Landscape vs Parameterization
Data Symmetries
Diffeomorphisms
Euclidean Neural Network
Paradoxes
\(D_f \propto |f(\tau x) - f(x)|\)
- average over inputs
- average over diffeomorphisms of the same temperature
- normalized by the amplitude of \(f\)
Sensitivity to diffeomorphisms
Landscape vs Parameterization
Data Symmetries
Diffeomorphisms
Euclidean Neural Network
Paradoxes
Landscape vs Parameterization
Data Symmetries
Diffeomorphisms
\(\displaystyle R_f = \frac{D_f}{G_f}\)
Euclidean Neural Network
Paradoxes
Leonardo Petrini et al arxiv 2105.02468
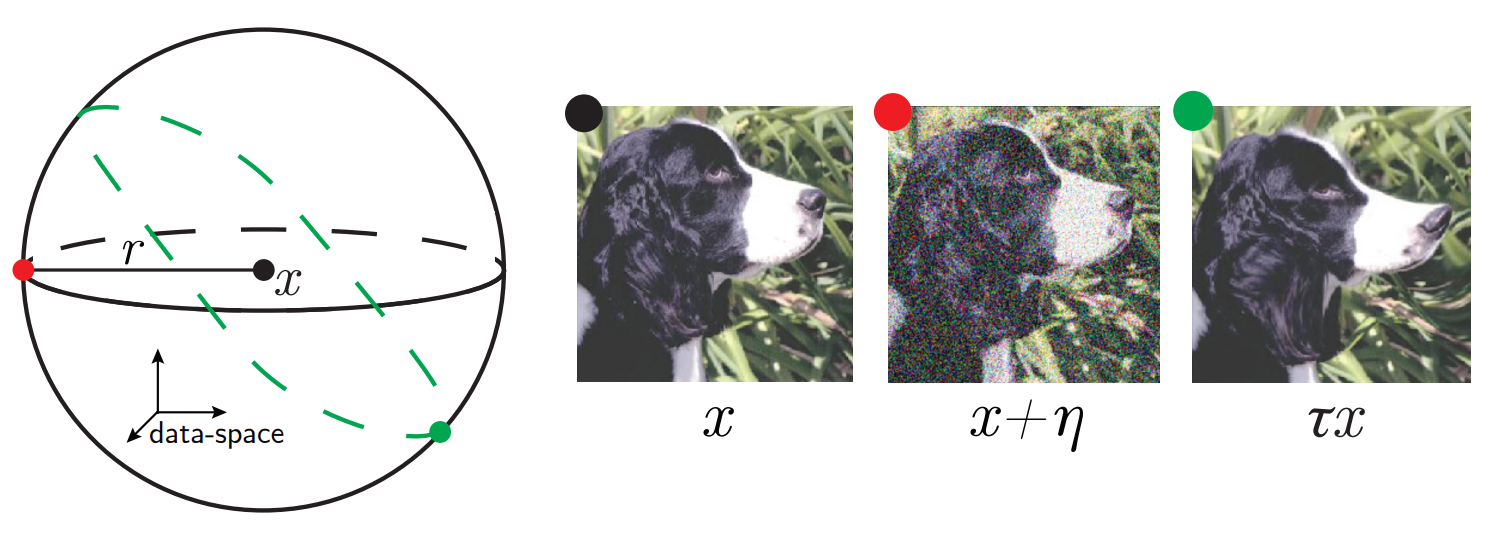
Relative Sensitivity
Landscape vs Parameterization
Data Symmetries
Diffeomorphisms

Euclidean Neural Network
Paradoxes
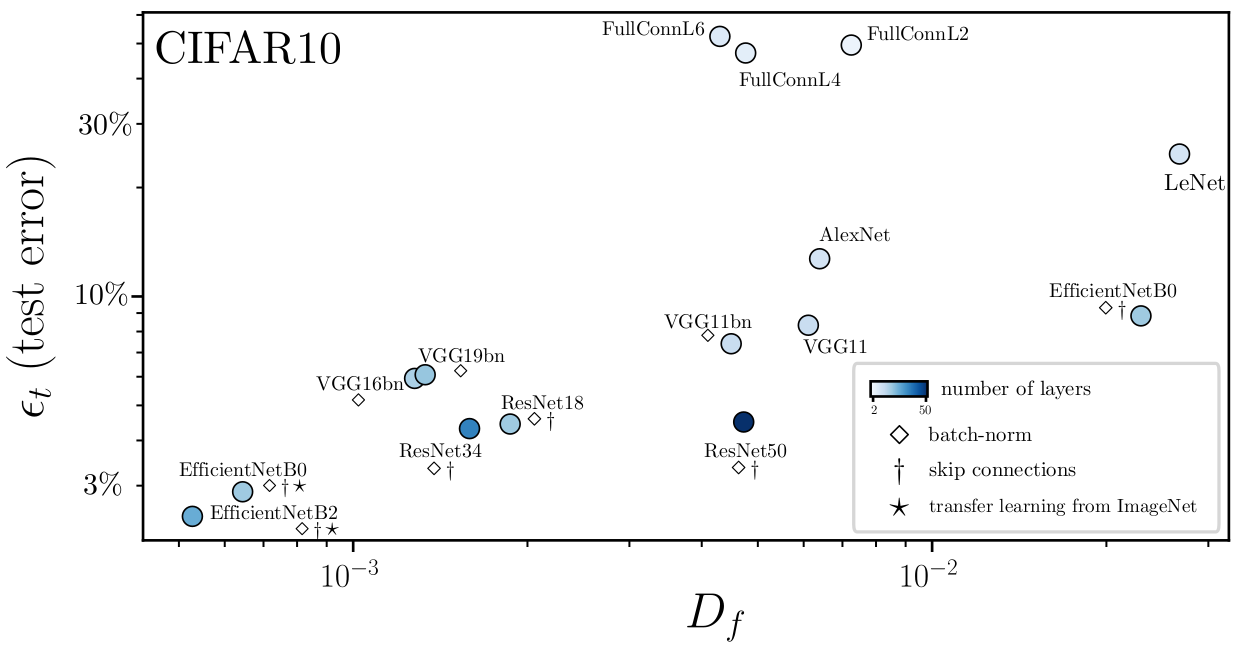
(Relative) Sensitivity to diffeomorphisms is key to beat the curse of dimensionality
Landscape vs Parameterization
Data Symmetries
Diffeomorphisms
Euclidean Neural Network
Euclidean Neural Network
Paradoxes
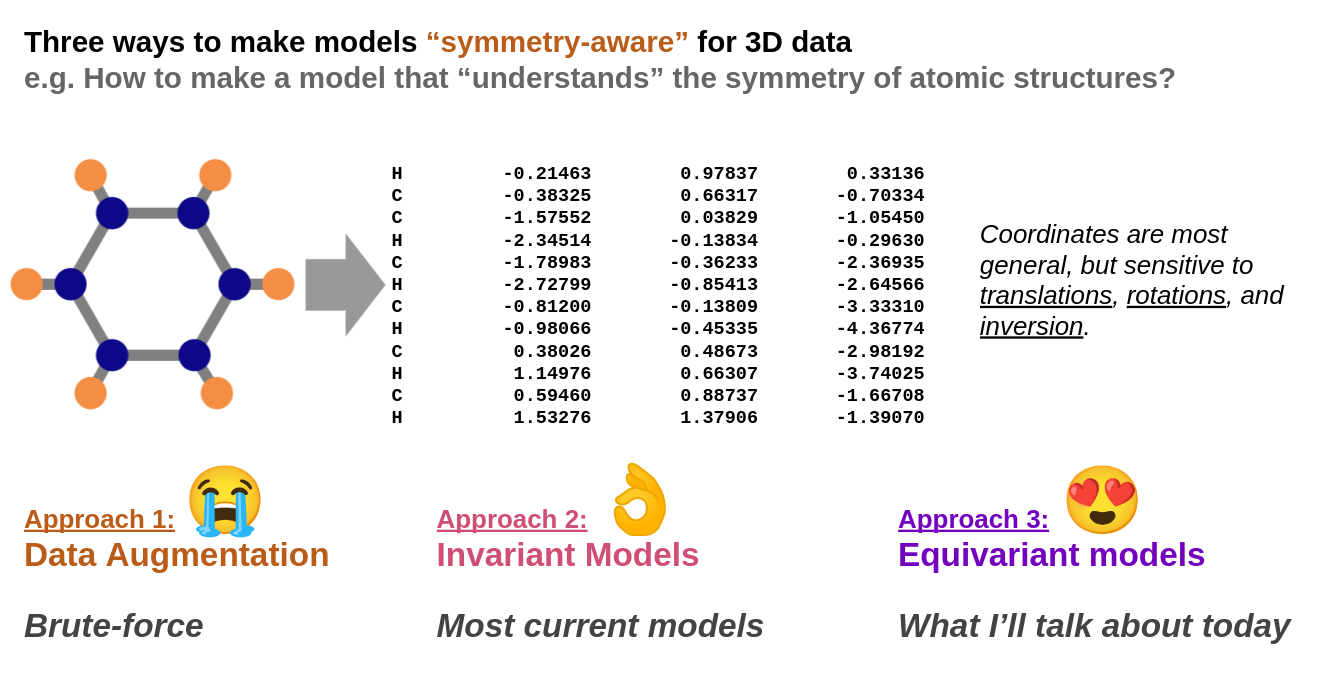
Can we generalize CNN invariance to other symmetries?
So far we looked at 2D images
Landscape vs Parameterization
Data Symmetries
Diffeomorphisms
Euclidean Neural Network
Paradoxes
Equivariance
\(f(w, {\color{blue}D(g)} x) = {\color{blue}D'(g)} f(w, x)\)
Classification with CNN translation identity
Segmentation with CNN translation translation
Aim rotation rotation
Landscape vs Parameterization
Data Symmetries
Diffeomorphisms
Euclidean Neural Network
Paradoxes

Daniel Worrall et al CVPR (2017)
CNN are not equivariant to rotations
Landscape vs Parameterization
Data Symmetries
Diffeomorphisms
Euclidean Neural Network
slide taken from Tess Smidt
Paradoxes
Landscape vs Parameterization
Data Symmetries
Diffeomorphisms
Euclidean Neural Network
Paradoxes
CNN are easy to implement, usual machine learning libraries provide functions to do so
Equivariant Neural Network for 3D rotations are less easy to implement and requires specialized functions
Landscape vs Parameterization
Data Symmetries
Diffeomorphisms
Euclidean Neural Network
Paradoxes
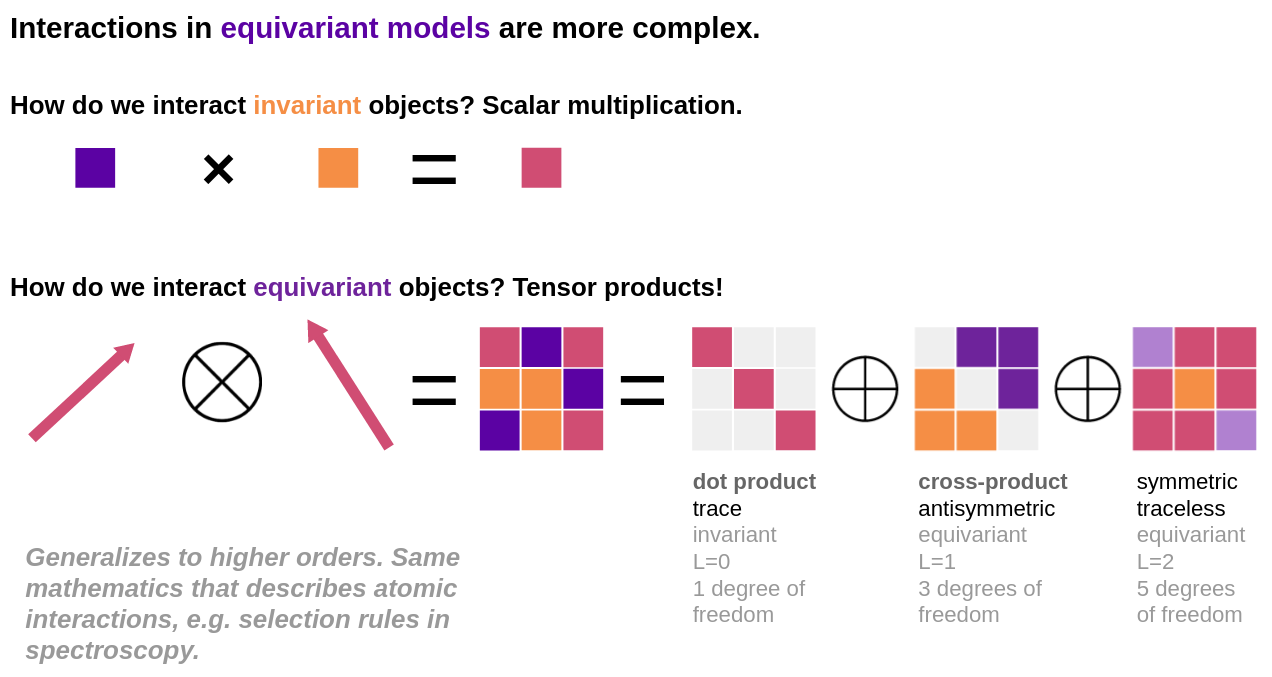
slide taken from Tess Smidt
Landscape vs Parameterization
Data Symmetries
Diffeomorphisms
Euclidean Neural Network
e3nn
open source library
pytorch and jax (e3nn-jax)
Efficient code for:
- spherical harmonics
- tensor product
Paradoxes
between any irreps of O(3)
Landscape vs Parameterization
Data Symmetries
Diffeomorphisms
Euclidean Neural Network
e3nn
is modular and flexible
The same building blocks allow to implement
- message passing on graph
- voxel convolution
- SE(3)-Transformers
- SphericalCNN
Paradoxes
Cohen, Geiger, et al (1801.10130)
Fabian Fuchs et al (2006.10503)
Weiler, Geiger et al (1807.02547)
Tess Smidt et al (1802.08219)
Landscape vs Parameterization
Data Symmetries
Diffeomorphisms
Euclidean Neural Network
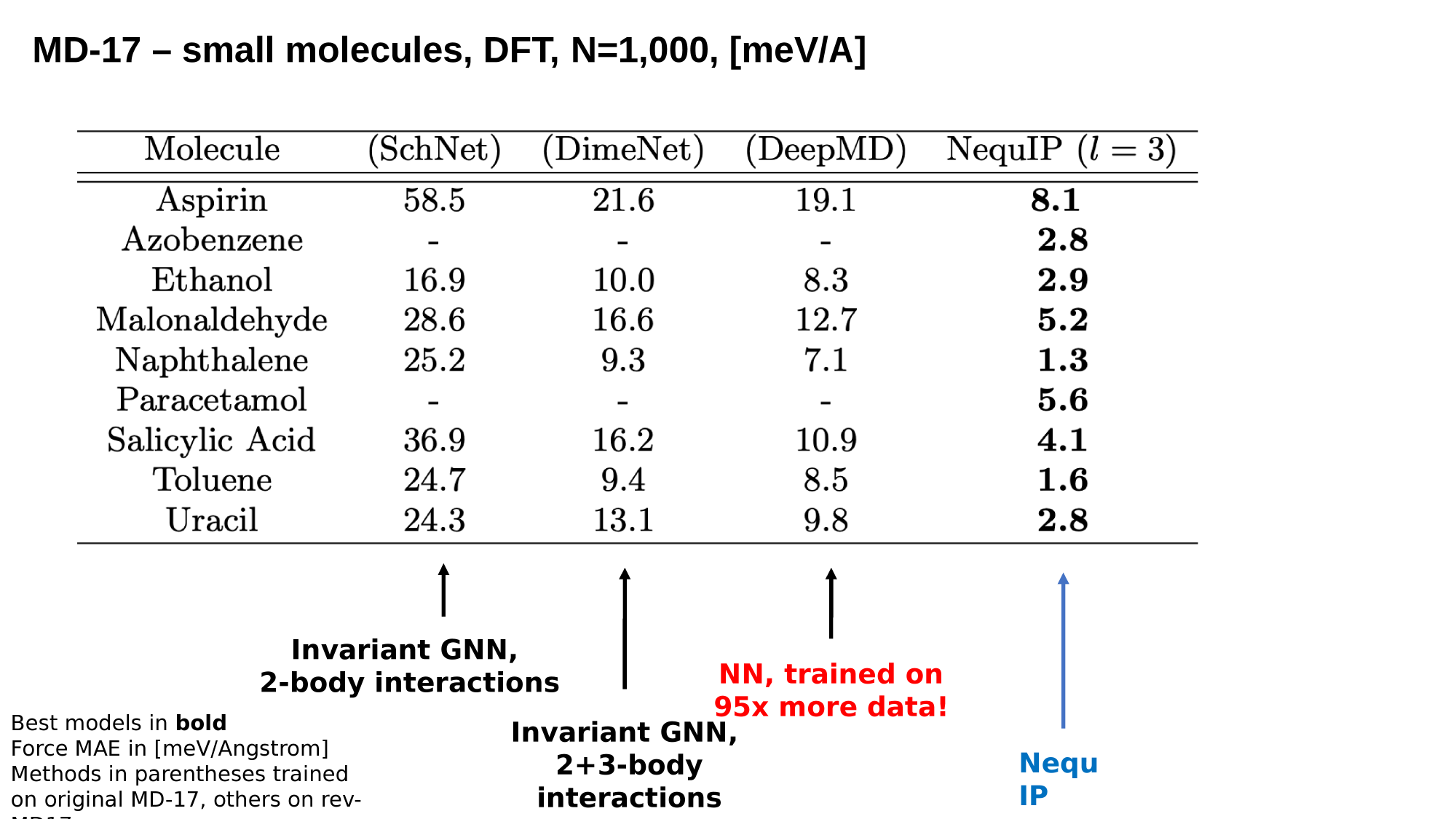
One example of results obtained using e3nn
Ab initio Molecular dynamics
Paradoxes
Simon Batzner et al (2021) arxiv 2101.03164
Landscape vs Parameterization
Data Symmetries
Paradoxes
Is stability to diffeomorphisms responsible for beating the curse of dimensionality?
- We see a strong correlation between the relative stability and the test error
- It is acquired during training
- How is it learned?
- Is there a bound between \(\epsilon\) and \(R_f\)?
Can we generalize CNN invariance to other symmetries?
- e3nn is equivariant to translations, rotations and mirror
- Why equivariant neural network perform better than invariant ones?
Thank you for your time
Slides for Ian's lab meeting
By Mario Geiger
Slides for Ian's lab meeting
- 775



