Árboles Binarios de Búsqueda
Mateo Sanabria Ardila
Estructura de Datos y Algoritmos

Árbol
Es un grafo conexo, aciclico.

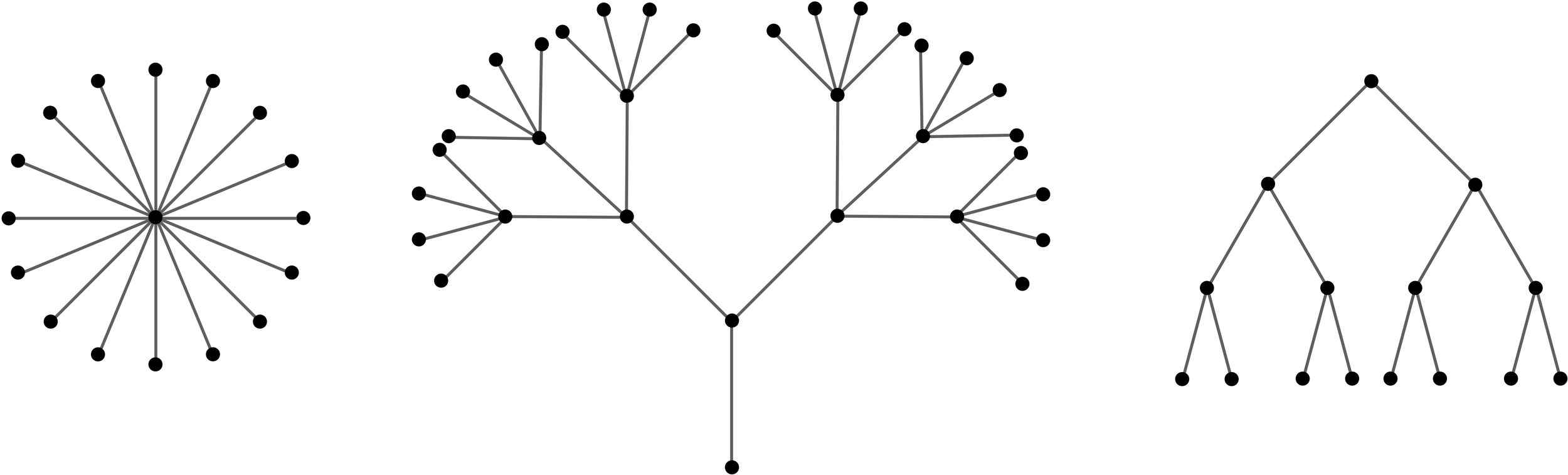


Árbol binario
Es un grafo conexo, aciclico tal que el grado de cada nodo no es mayor a 2.





BST
Árbol binario de busqueda
Es un árbol binario donde cada nodo tiene una llave y un valor donde:
La llave en cualquier nodo es más grande que cualquier llave en el subárbol izquierdo y más pequeña que las llaves en el subarbol derecho.
Es un árbol binario donde cada nodo tiene una llave y un valor donde:
La llave en cualquier nodo es más grande que cualquier llave en el subárbol izquierdo y más pequeña que las llaves en el subarbol derecho.
BST
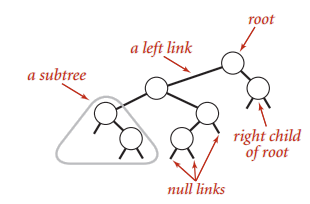
La llave en cualquier nodo es más grande que cualquier llave en el subárbol izquierdo y más pequeña que las llaves en el subarbol derecho.
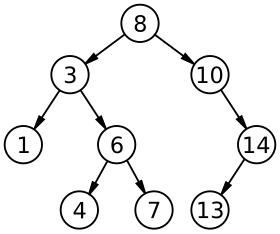
Para que sirve esta estructura de datos?
(BST)

Existe el elemento con llave K:12?
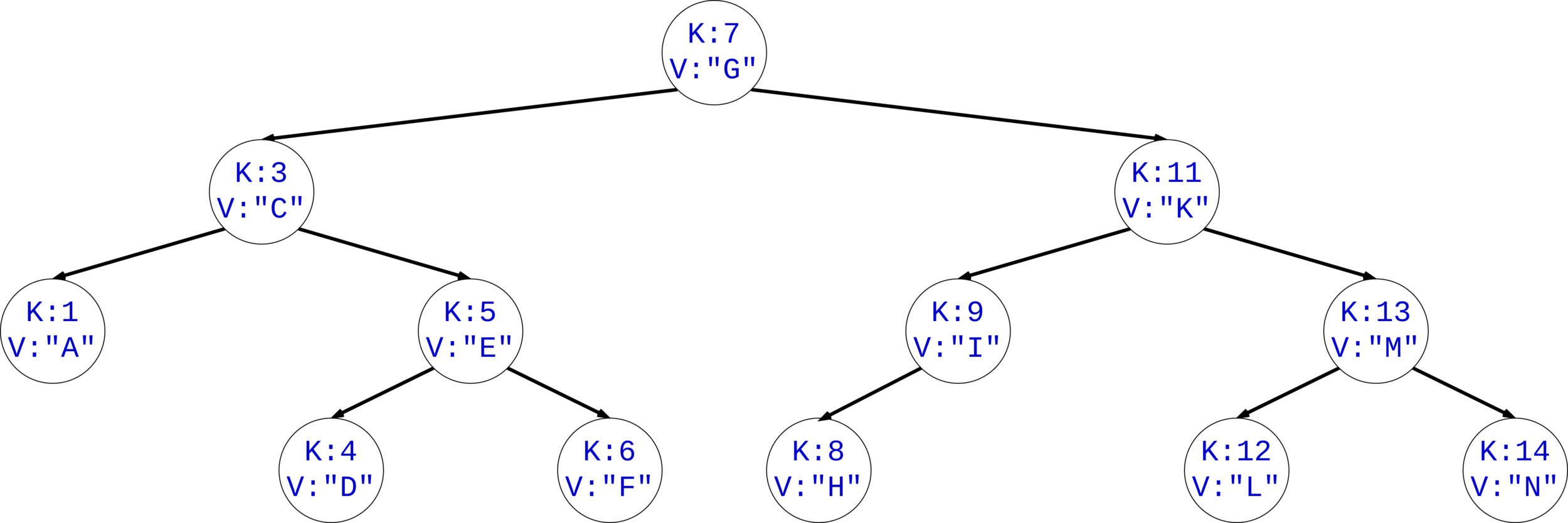
Existe el elemento con llave K:12?

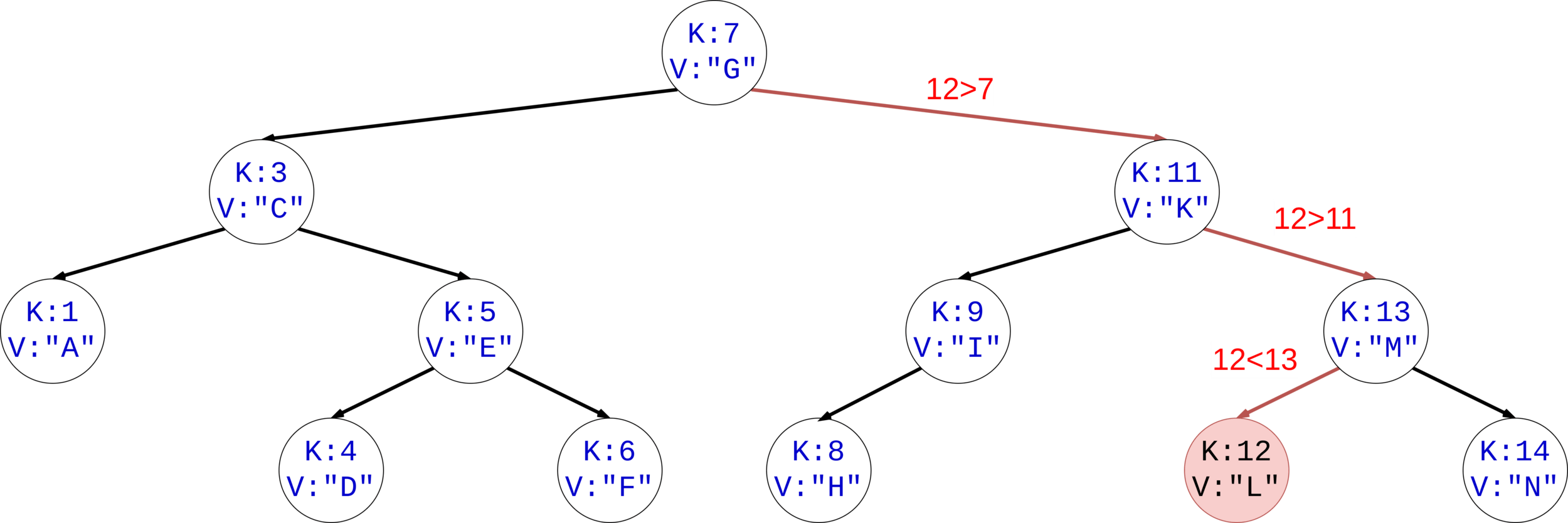
Existe el elemento con llave K:10?

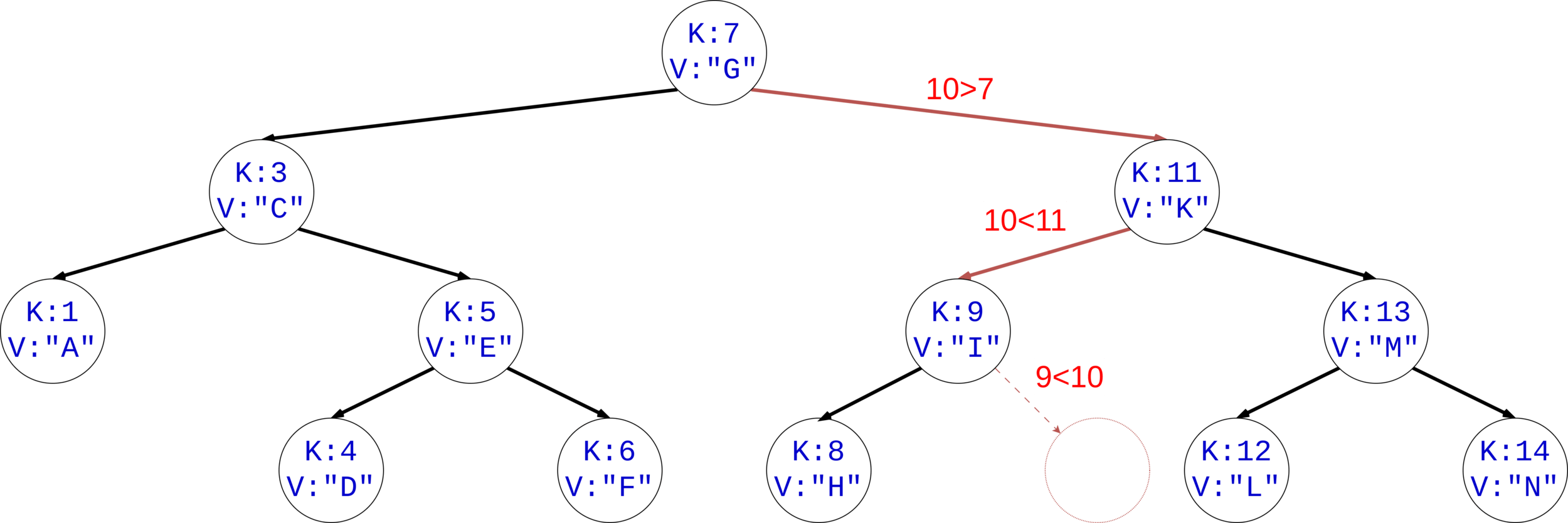
BST en Python
-
Node (BST) -
get (search) -
put (insert) -
delete -
max/min
-
rank
Node
-
key: LLave del nodo
-
value: Valor del nodo
-
size: Tamaño subarbol
-
left: Subarbol izquierdo
-
right: Subarbol derecho
def newNode(key, value, size):
node = {'key': key,
'value': value,
'size': size,
'left': None,
'right': None,
'type': 'BST'}
return nodeBST
def newBST(omaptype, cmpfunction, datastructure):
try:
bst = {'root': None,
'cmpfunction': cmpfunction,
'type': omaptype,
'datastructure': datastructure}
if(cmpfunction is None):
bst['cmpfunction'] = defaultfunction
else:
bst['cmpfunction'] = cmpfunction
return bst
except Exception as exp:
error.reraise(exp, 'BST:NewMap')GET
def get(bst, key):
try:
node = getNode(bst['root'], key, bst['cmpfunction'])
return node
except Exception as exp:
error.reraise(exp, 'Bst:get')GETNode
def getNode(root, key, cmpfunction):
try:
node = None
if (root is not None):
# Comparar llaves con la de nodo actual
cmp = cmpfunction(key, root['key'])
if (cmp == 0):
node = root
elif (cmp < 0):
# Si es menor -> Busqueda en la izq
node = getNode(root['left'], key, cmpfunction)
else:
# Si es mayor -> Busqueda en la der
node = getNode(root['right'], key, cmpfunction)
# Si el nodo actual es None, se retorna None
return node
except Exception as exp:
error.reraise(exp, 'BST:getNode')put
def put(bst, key, value):
try:
bst['root'] = insertNode(bst['root'],
key,
value,
bst['cmpfunction'])
return bst
except Exception as exp:
error.reraise(exp, 'Bst:Put')insertNode
def insertNode(root, key, value, cmpfunction):
try:
if (root is None):
root = bstnode.newNode(key, value, 1)
else:
cmp = cmpfunction(key, root['key'])
# La llave a insertar es menor que la raiz
if (cmp < 0):
root['left'] = insertNode(root['left'], key, value, cmpfunction)
# La llave a insertar es mayor que la raiz
elif (cmp > 0):
root['right'] = insertNode(root['right'], key, value, cmpfunction)
# La llave a insertar es igual que la raiz
else:
root['value'] = value
leftsize = sizeTree(root['left'])
rightsize = sizeTree(root['right'])
root['size'] = 1 + leftsize + rightsize
return root
except Exception as exp:
error.reraise(exp, 'BST:insertNode')BST: put
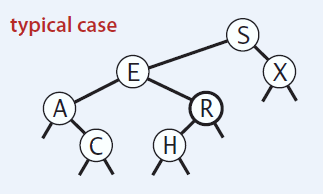
La estructura de un BST puede variar dependiendo del orden en el que se hacen los puts de los nodos

BST: put
La estructura de un BST puede variar dependiendo del orden en el que se hacen los puts de los nodos: las llaves llegan en orden tal que el arbol esta balanceado
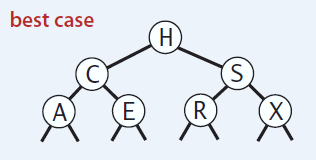
BST: put
La estructura de un BST puede variar dependiendo del orden en el que se hacen los puts de los nodos: las llaves llegan siempre en orden decreciente/creciente
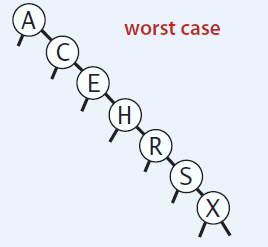
BST: put
La estructura de un BST puede variar dependiendo del orden en el que se hacen los puts de los nodos: las llaves llega en desorden
DELETE
def delete(bst, key):
try:
bst['root'] = deleteNode(bst['root'],
key,
bst['cmpfunction'])
return bst
except Exception as exp:
error.reraise(exp, 'Bst:Remove')DELETENode
Esta operación no es tan 'fácil'!

DELETENode
Opción 0:Dejar el valor en None, la clave queda en el árbol para guiar la búsqueda
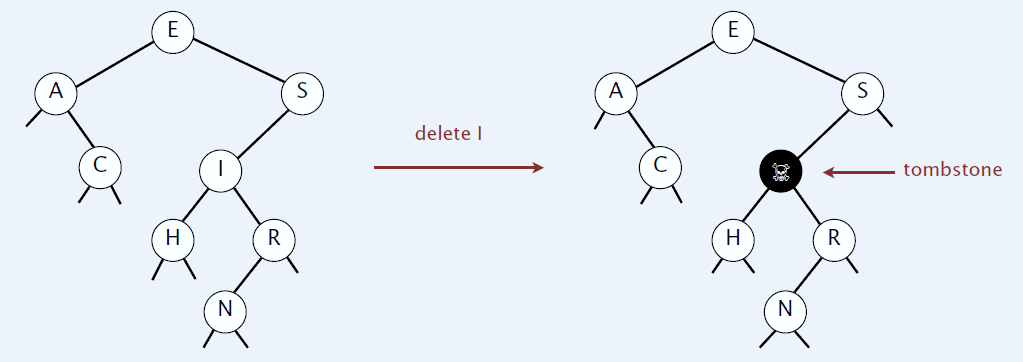
DELETENode
Opción 1:Borrar el nodo
-
Caso 0: No tiene hijos, cambiar referencia del padre a None
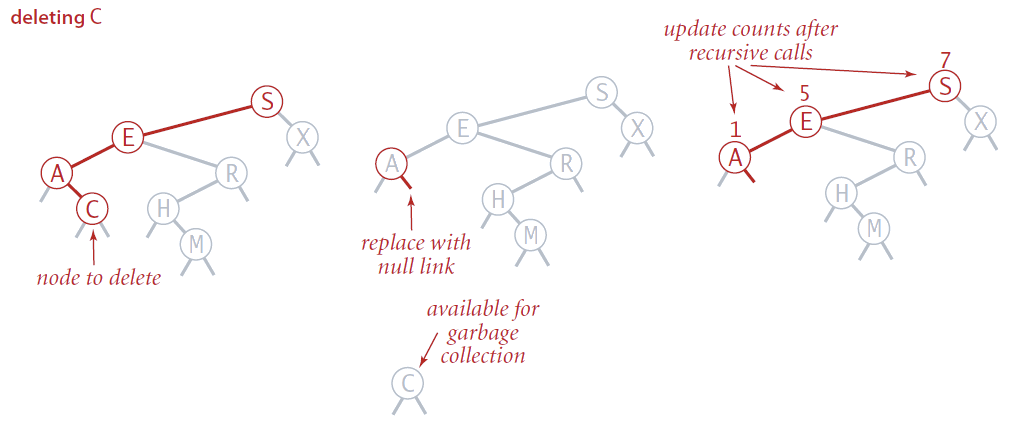
DELETENode
Opción 1:Borrar el nodo
-
Caso 1: Tiene 1 hijo, “darle el hijo al abuelo”
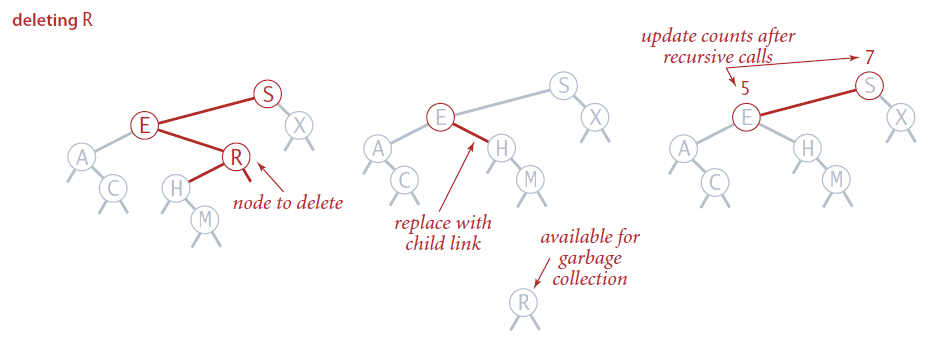
DELETENode
Opción 1:Borrar el nodo
-
Caso 2: Tiene 2 hijos
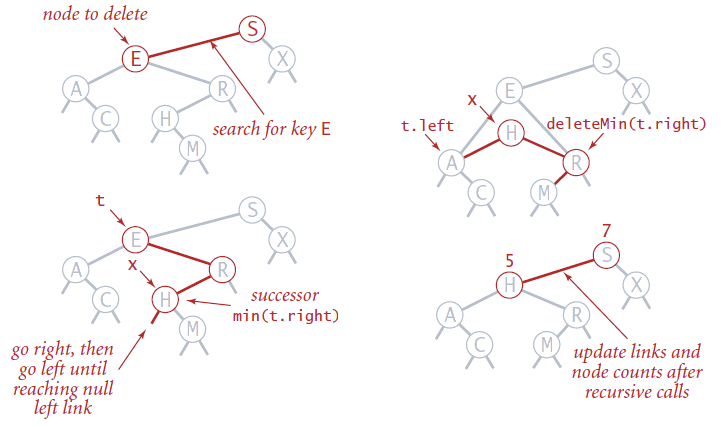
DeleteNode
def deleteNode(root, key, cmpfunction):
try:
if (root is not None):
cmp = cmpfunction(key, root['key'])
if (cmp == 0): # La llave es la que se busca
if (root['right'] is None): # No tiene hijo derecho
return root['left']
elif (root['left'] is None): # No tiene hijo izquierdo
return root['right']
else: # se cambia por el menor de los mayores
elem = root
root = minKeyNode(elem['right'])
root['right'] = deleteMinTree(elem['right'])
root['left'] = elem['left']
elif (cmp < 0):
root['left'] = deleteNode(root['left'], key, cmpfunction)
else:
root['right'] = deleteNode(root['right'], key, cmpfunction)
root['size'] = 1 + sizeTree(root['left']) + sizeTree(root['right'])
return root
except Exception as exp:
error.reraise(exp, 'BST:deleteNode')
Arboles Binarios de Busqueda
By Mateo Sanabria Ardila
Arboles Binarios de Busqueda
Arboles Binarios de Busqueda
- 281



