Quantum Mechanics
M. Rocha
Physics 4C
The Wave-Particle Duality
In order to explain the double slit experiments, both electrons and photons must have wave properties in an individual basis
A photon/electron behaves as a particle when it is being emitted by an atom or absorbed by photographic film or detector, and behaves as a wave in traveling from a source to the place where it is detected
The Wave-Particle Duality
Matter Waves
If matter particles behave like waves, then they must have a wavelength. In 1924 Louis de Broglie found that the wavelength of matter is given by Plank's constant divided by the momentum of the particle
Wavelength=Momentumhβ,
\mathrm{Wavelength} = \frac{h}{\mathrm{Momentum}},
Wavelength of matter waves
From the above we can get an equation for the momentum as a function of the wavenumber π=2π/π
pβ=Ξ»hβ=2Οhkβ=βk
\vec{p} = \frac{h}{\lambda} = \frac{hk}{2 \pi} = \hbar \vec{k} \\
Ξ»=pβhβ
\lambda = \frac{h}{\vec{p}} \\
de Broglie also stated that the energy of matter waves is given by πΈ=βπ, where π the frequency of the wave.
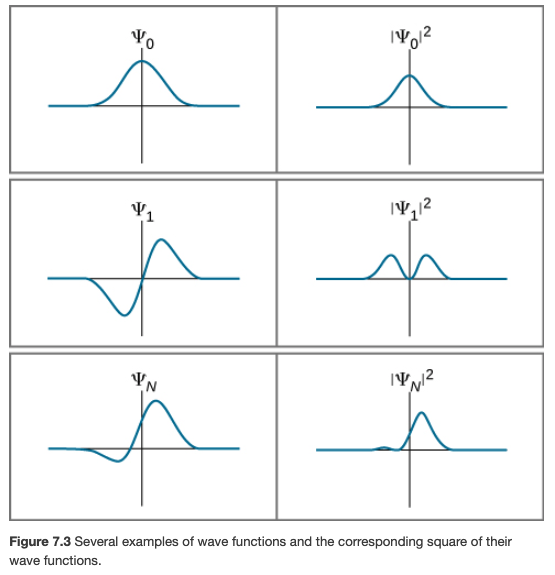
Probability Density
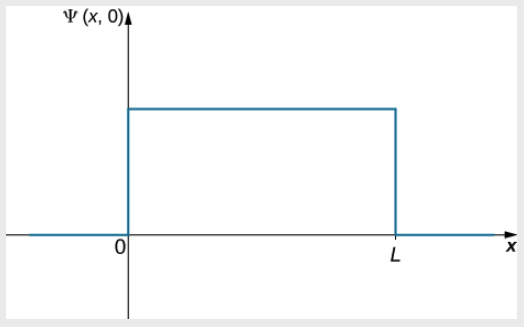
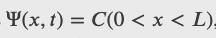
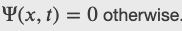
A ball is constrained to move along a line inside a tube of length L. The ball is equally likely to be found anywhere in the tube at some time t. What is the probability of finding the ball in the left half of the tube at that time?
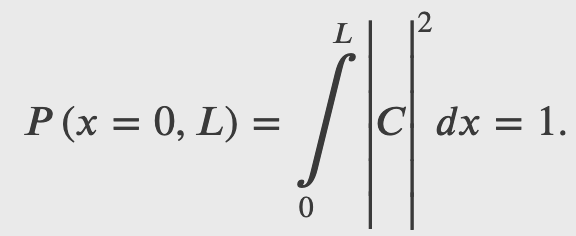
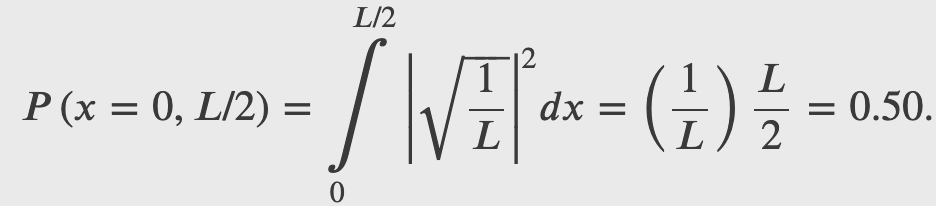
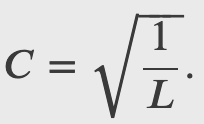
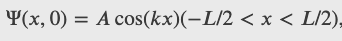
A ball is again constrained to move along a line inside a tube of length L. This time, the ball is found preferentially in the middle of the tube. One way to represent its wave function is with a simple cosine function. What is the probability of finding the ball in the last one-quarter of the tube?
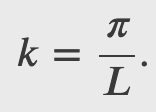
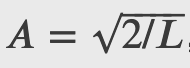
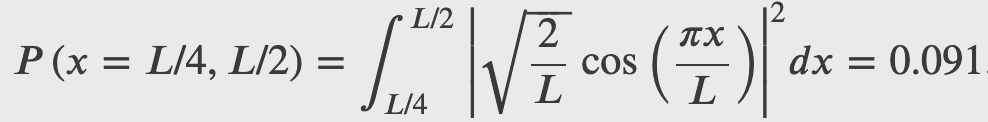
Free Particle and Heisenberg's Uncertainty Principle
Consider a free electron that moves along the x-direction. The electron moves with a constant velocity u and momentum π=ππ’. It seems plausible to assume a classical/real oscillating wave function of the form
where we have used de Broglieβs relations, π=βπ, for the last step.
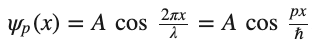
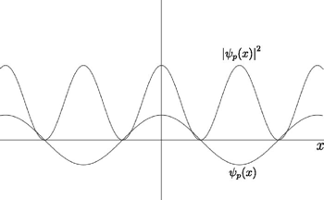
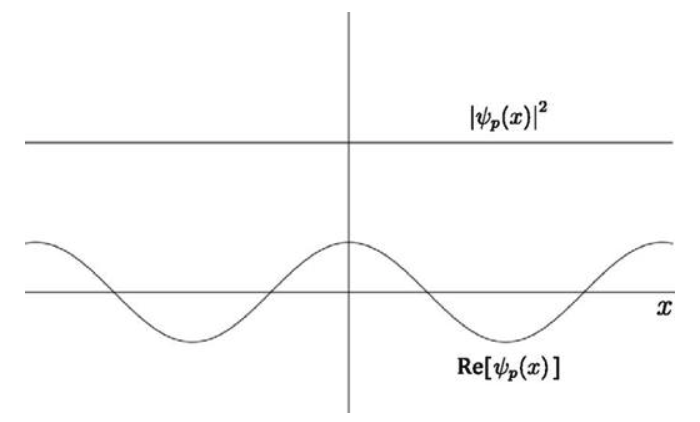
But as shown in the graph of β£Οp(x)β£^2 below, the above wave function would be in contradiction to Heisenberg's Uncertainty Principle. If you know the momentum of the electron exactly, you should have no information about its position.
Free Particle and Heisenberg's Uncertainty Principle
Is there a function that has a wavelength and, yet, a constant absolute value? The complex exponential has this property. Therefore, we need the wave function of a free particle to be of the form
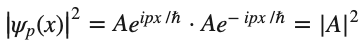
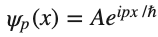
so
Which is consistent with the Heisenberg's Uncertainty Principle. If you know the momentum of the electron exactly, you should have no information about its position.
eiΟ=cosΟ+isinΟ
e^{i\phi} = \cos{\phi}+i \sin{\phi}
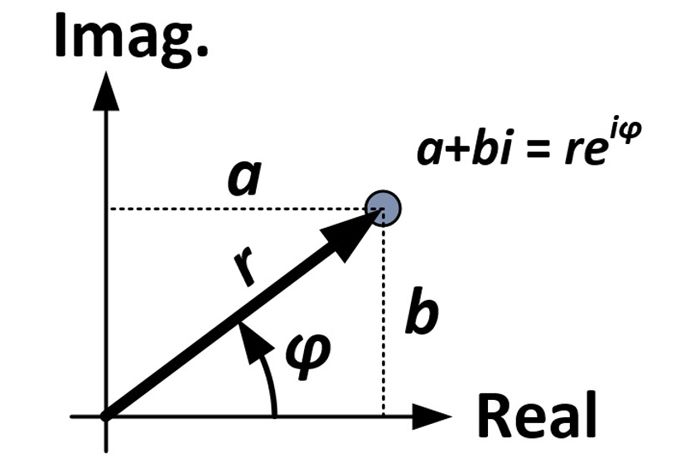
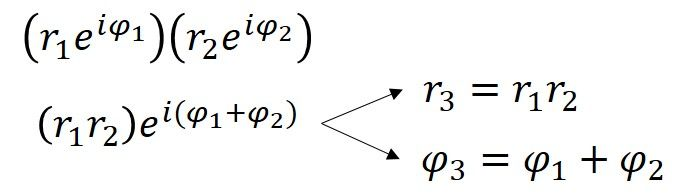
The multiplication of two complex numbers represents a dilation and a rotation
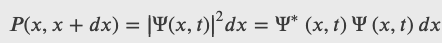
Complex Conjugates
Realistic physical wave functions are usually complex functions. A complex function is one that contains one or more imaginary numbers. Experimental measurements produce real numbers only, so the procedure to use the wave function must be slightly modified. In general, the probability that a particle is found in the narrow interval (x, x + dx) at time t is given by
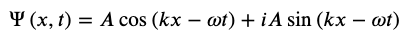
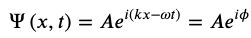
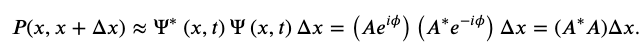
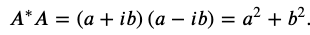
Wave Function of Free Particle
In QM The wave function of a particle that experiences no forces moving at constant velocity along the x-direction is given by
Wave Packet (Localized Particle) and Heisenberg's Uncertainty Principle
ΞpΞxβ₯2Οhβ
\Delta p \Delta x \geq \frac{h}{2 \pi}
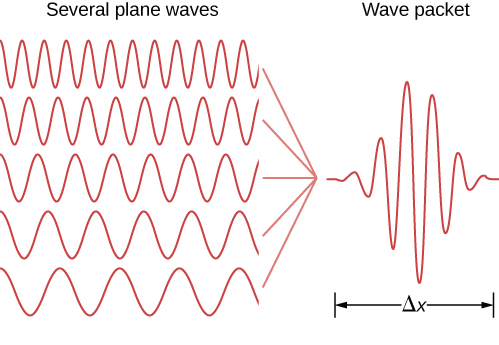
Heisenberg's Uncertainty Principle
ΞpΞxβ₯2Οhβ
\Delta p \Delta x \geq \frac{h}{2 \pi}
High accuracy in position => large uncertainty in momentum
High accuracy in momentum => large uncertainty in position
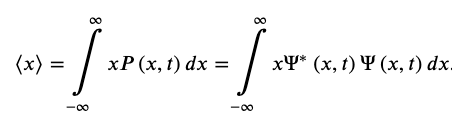
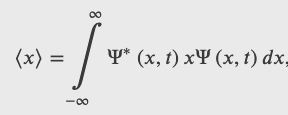
The Expectation Value of The Position
Position Operator
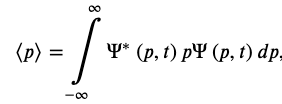
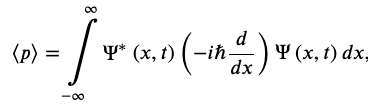
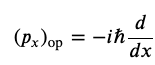
The Expectation Value of The Momentum
Momentum Operator in the x-direction
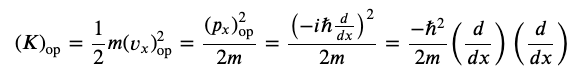
Kinetic Energy Operator
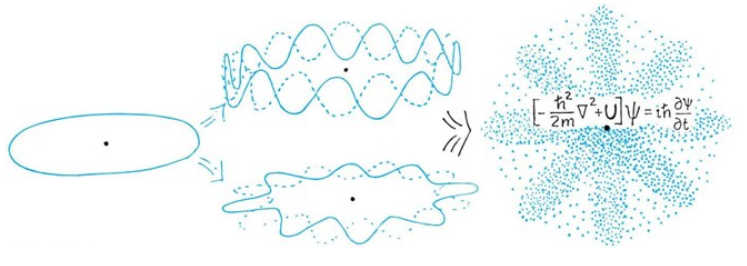
The Wave Function of Electrons in a Hydrogen Ataom
The Schrodinger's Wave Equation
For this we need an energy-momentum equation. For example the energy-momentum equation of a classical non-relativistic particle is given by
The Schrodinger's equation describes the dynamics of quantum system when they are subject to forces, i.e. when there are potential energies involved.
The Schrodinger's equation is the energy-momentum equation of a quantum system represented by a wave function
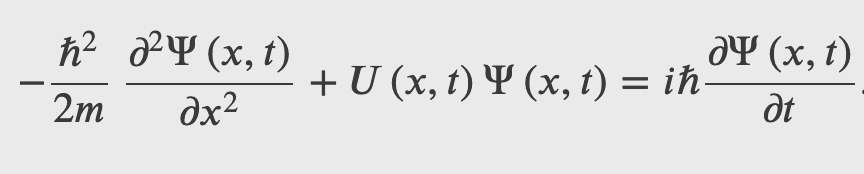
The Schrodinger's Wave Equation
Notice that for U(x,t) = 0, the Schrodinger's equation reduces to
A valid solution to this equation is the wave function of a free particle
Also if U does not depend on time, it is possible to show that
and since πΈ=βπ the Schrodinger's can be written as
Quantum Particle In a Box
But the following must be true:
The most general possible solution is
Thus
Quantum Particle In a Box
The End
Quantum Mechanics M. Rocha Physics 4C
Quantum Mechanics - Physics 4C
By Miguel Rocha
Quantum Mechanics - Physics 4C
Physics 1 - Week 14 - Chapter 31-32
- 314
