BE3024 - Sistemas de Control 1 (Biomédica)
2do ciclo, 2024
Lección 13: Sistemas no lineales y linealización
Un último detalle
\dot{v}=v-\dfrac{v^3}{3}-w+RI_\mathrm{ext} \\
\tau\dot{w}=v+a-bw
modelo FitzHugh–Nagumo
Simplificación en 2D del modelo Hodgkin–Huxley que describe cómo se inician y transmiten los potenciales de acción en las neuronas.
\dot{v}=v-\dfrac{v^3}{3}-w+RI_\mathrm{ext} \\
\tau\dot{w}=v+a-bw
modelo FitzHugh–Nagumo
\dot{v}=v-\dfrac{v^3}{3}-w+RI_\mathrm{ext} \\
\tau\dot{w}=v+a-bw
\begin{bmatrix} x_1 \\ x_2 \end{bmatrix}=\begin{bmatrix} v \\ w \end{bmatrix}
voltaje de membrana
reactivación del canal de sodio y desactivación del canal de potasio
u=I_\mathrm{ext}
estímulo externo
\dot{x}_1=x_1-\frac{1}{3}x_1^3-x_2+Ru \\
\dot{x}_2=\frac{1}{\tau}x_1-\frac{b}{\tau}x_2+\frac{a}{\tau}
\Rightarrow
\dot{x}_1=x_1-\frac{1}{3}x_1^3-x_2+Ru \\
\dot{x}_2=\frac{1}{\tau}x_1-\frac{b}{\tau}x_2+\frac{a}{\tau}
\Rightarrow
¿Cuál es el problema con esto?
\dot{x}_1=x_1-\frac{1}{3}x_1^3-x_2+Ru \\
\dot{x}_2=\frac{1}{\tau}x_1-\frac{b}{\tau}x_2+\frac{a}{\tau}
\Rightarrow
¿Cuál es el problema con esto?
Es imposible de colocar en la forma estándar sólo con un cambio de variables
\dot{\mathbf{x}}=\mathbf{A}\mathbf{x}+\mathbf{B}\mathbf{u}
\dot{x}_1=x_1-\frac{1}{3}x_1^3-x_2+Ru \\
\dot{x}_2=\frac{1}{\tau}x_1-\frac{b}{\tau}x_2+\frac{a}{\tau}
\Rightarrow
¿Cuál es el problema con esto?
Es imposible de colocar en la forma estándar sólo con un cambio de variables
\dot{\mathbf{x}}=\mathbf{A}\mathbf{x}+\mathbf{B}\mathbf{u}
Esto es porque el sistema presenta una forma más general, que corresponde a la de un sistema no lineal.
\begin{cases} \dot{\mathbf{x}}=\mathbf{f}\left(\mathbf{x}, \mathbf{u}\right) \\
\mathbf{y}=\mathbf{h}\left(\mathbf{x}\right) \end{cases}
\dot{x}_1=x_1-\frac{1}{3}x_1^3-x_2+Ru \\
\dot{x}_2=\frac{1}{\tau}x_1-\frac{b}{\tau}x_2+\frac{a}{\tau}
\Rightarrow
¿Cuál es el problema con esto?
Es imposible de colocar en la forma estándar sólo con un cambio de variables
\dot{\mathbf{x}}=\mathbf{A}\mathbf{x}+\mathbf{B}\mathbf{u}
Esto es porque el sistema presenta una forma más general, que corresponde a la de un sistema no lineal.
\begin{cases} \dot{\mathbf{x}}=\mathbf{f}\left(\mathbf{x}, \mathbf{u}\right) \\
\mathbf{y}=\mathbf{h}\left(\mathbf{x}\right) \end{cases}
\(\mathbf{f}\) y \(\mathbf{h}\) son campos vectoriales, es decir, las ecuaciones ya no pueden reordenarse en forma de matrices y vectores.
Para el modelo FitzHugh–Nagumo entonces
\begin{bmatrix} \dot{x}_1 \\ \dot{x}_2 \end{bmatrix}=
\begin{bmatrix} x_1-\frac{1}{3}x_1^3-x_2+Ru \\ \frac{1}{\tau}x_1-\frac{b}{\tau}x_2+\frac{a}{\tau} \end{bmatrix} \\
y=x_1
(por ejemplo)
Para el modelo FitzHugh–Nagumo entonces
\begin{bmatrix} \dot{x}_1 \\ \dot{x}_2 \end{bmatrix}=
\begin{bmatrix} x_1-\frac{1}{3}x_1^3-x_2+Ru \\ \frac{1}{\tau}x_1-\frac{b}{\tau}x_2+\frac{a}{\tau} \end{bmatrix} \\
y=x_1
(por ejemplo)
\dot{\mathbf{x}}
\mathbf{f}\left(\mathbf{x},\mathbf{u}\right)
f_1\left(\mathbf{x},\mathbf{u}\right)
f_2\left(\mathbf{x},\mathbf{u}\right)
\mathbf{h}\left(\mathbf{x}\right)
para el modelo FitzHugh–Nagumo entonces
\begin{bmatrix} \dot{x}_1 \\ \dot{x}_2 \end{bmatrix}=
\begin{bmatrix} x_1-\frac{1}{3}x_1^3-x_2+Ru \\ \frac{1}{\tau}x_1-\frac{b}{\tau}x_2+\frac{a}{\tau} \end{bmatrix} \\
y=x_1
(por ejemplo)
\dot{\mathbf{x}}
\mathbf{f}\left(\mathbf{x},\mathbf{u}\right)
f_1\left(\mathbf{x},\mathbf{u}\right)
f_2\left(\mathbf{x},\mathbf{u}\right)
\mathbf{h}\left(\mathbf{x}\right)
% Parámetros del sistema
a = 0.7;
b = 0.8;
tau = 12.5;
R = 0.1;
Iext = 0.5;
% Variables y funciones simbólicas
syms x1 x2 u
f(x1, x2, u) = [ x1 - x1^3/3 - x2 + R*u;
x1/tau - b*x2/tau + a/tau]
h(x1, x2) = x1para el modelo FitzHugh–Nagumo entonces
\begin{bmatrix} \dot{x}_1 \\ \dot{x}_2 \end{bmatrix}=
\begin{bmatrix} x_1-\frac{1}{3}x_1^3-x_2+Ru \\ \frac{1}{\tau}x_1-\frac{b}{\tau}x_2+\frac{a}{\tau} \end{bmatrix} \\
y=x_1
(por ejemplo)
\dot{\mathbf{x}}
\mathbf{f}\left(\mathbf{x},\mathbf{u}\right)
f_1\left(\mathbf{x},\mathbf{u}\right)
f_2\left(\mathbf{x},\mathbf{u}\right)
\mathbf{h}\left(\mathbf{x}\right)
% Parámetros del sistema
a = 0.7;
b = 0.8;
tau = 12.5;
R = 0.1;
Iext = 0.5;
% Variables y funciones simbólicas
syms x1 x2 u
f(x1, x2, u) = [ x1 - x1^3/3 - x2 + R*u;
x1/tau - b*x2/tau + a/tau]
h(x1, x2) = x1¿Qué hacemos con esto?
Debemos transformar el modelo no lineal a un modelo LTI para poder aplicar las técnicas que hemos visto.
para el modelo FitzHugh–Nagumo entonces
\begin{bmatrix} \dot{x}_1 \\ \dot{x}_2 \end{bmatrix}=
\begin{bmatrix} x_1-\frac{1}{3}x_1^3-x_2+Ru \\ \frac{1}{\tau}x_1-\frac{b}{\tau}x_2+\frac{a}{\tau} \end{bmatrix} \\
y=x_1
(por ejemplo)
\dot{\mathbf{x}}
\mathbf{f}\left(\mathbf{x},\mathbf{u}\right)
f_1\left(\mathbf{x},\mathbf{u}\right)
f_2\left(\mathbf{x},\mathbf{u}\right)
\mathbf{h}\left(\mathbf{x}\right)
% Parámetros del sistema
a = 0.7;
b = 0.8;
tau = 12.5;
R = 0.1;
Iext = 0.5;
% Variables y funciones simbólicas
syms x1 x2 u
f(x1, x2, u) = [ x1 - x1^3/3 - x2 + R*u;
x1/tau - b*x2/tau + a/tau]
h(x1, x2) = x1¿Qué hacemos con esto?
Debemos transformar el modelo no lineal a un modelo LTI para poder aplicar las técnicas que hemos visto.
\(\Rightarrow\) linealización
Linealización alrededor de puntos de equilibrio
Para obtener un modelo LTI a partir de un sistema no lineal requerimos dos ingredientes:
- Un punto de equilibrio del sistema no lineal.
- Los jacobianos del sistema no lineal.
Puntos de equilibrio
El par \(\left(\mathbf{x}^*,\mathbf{u}^*\right)\) es un punto de equilibrio del sistema no lineal \(\dot{\mathbf{x}}=\mathbf{f}\left(\mathbf{x}, \mathbf{u}\right)\) si se cumple que
\mathbf{f}\left(\mathbf{x}^*,\mathbf{u}^*\right)=\mathbf{0}
es decir, es un punto en donde el sistema no evoluciona.
Puntos de equilibrio
El par \(\left(\mathbf{x}^*,\mathbf{u}^*\right)\) es un punto de equilibrio del sistema no lineal \(\dot{\mathbf{x}}=\mathbf{f}\left(\mathbf{x}, \mathbf{u}\right)\) si se cumple que
\mathbf{f}\left(\mathbf{x}^*,\mathbf{u}^*\right)=\mathbf{0}
es decir, es un punto en donde el sistema no evoluciona.
Estos se encuentran como la solución de un sistema no lineal de ecuaciones algebraicas.
¿Puntos de equilibrio para el modelo FitzHugh–Nagumo?
\dot{\mathbf{x}}=\mathbf{f}\left(\mathbf{x},\mathbf{u}\right)=
\begin{bmatrix} x_1-\frac{1}{3}x_1^3-x_2+Ru \\ \frac{1}{\tau}x_1-\frac{b}{\tau}x_2+\frac{a}{\tau} \end{bmatrix}
\mathbf{f}\left(\mathbf{x}^*,\mathbf{u}^*\right)=
\begin{bmatrix} x_1^*-\frac{1}{3}(x_1^*)^3-x_2^*+Ru^* \\ \frac{1}{\tau}x_1^*-\frac{b}{\tau}x_2^*+\frac{a}{\tau} \end{bmatrix}=\begin{bmatrix} 0 \\ 0 \end{bmatrix}
Resolver esto a mano puede llegar a ser complicado y en algunos casos incluso imposible.
\mathbf{f}\left(\mathbf{x}^*,\mathbf{u}^*\right)=
\begin{bmatrix} x_1^*-\frac{1}{3}(x_1^*)^3-x_2^*+Ru^* \\ \frac{1}{\tau}x_1^*-\frac{b}{\tau}x_2^*+\frac{a}{\tau} \end{bmatrix}=\begin{bmatrix} 0 \\ 0 \end{bmatrix}
Resolver esto a mano puede llegar a ser complicado y en algunos casos incluso imposible.
\mathbf{f}\left(\mathbf{x}^*,\mathbf{u}^*\right)=
\begin{bmatrix} x_1^*-\frac{1}{3}(x_1^*)^3-x_2^*+Ru^* \\ \frac{1}{\tau}x_1^*-\frac{b}{\tau}x_2^*+\frac{a}{\tau} \end{bmatrix}=\begin{bmatrix} 0 \\ 0 \end{bmatrix}
¿Qué hacemos entonces? Acudimos a MATLAB.
sol = solve(f(x1, x2, u) == [0; 0], {x1, x2, u})MATLAB retorna tres posibles soluciones
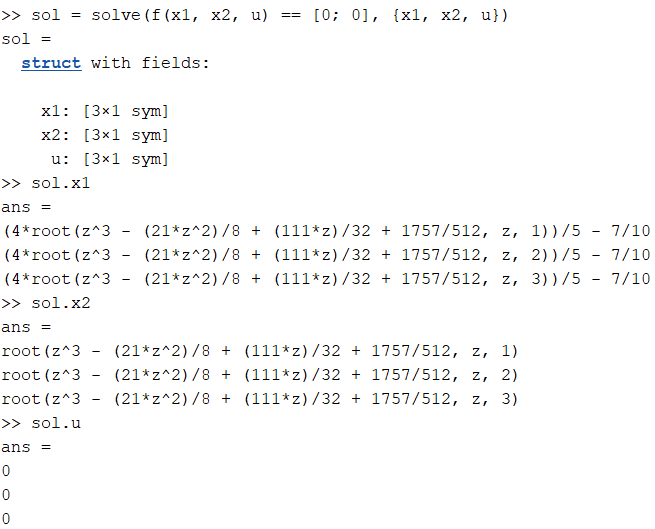
MATLAB retorna tres posibles soluciones
¿Cuál seleccionamos? La que requiera el contexto del problema.
Supongamos que en este caso nos interesa la primera solución. Entonces:
x1eq = double(sol.x1(1))
x2eq = double(sol.x2(1))
ueq = double(sol.u(1))\left(\mathbf{x}^*,\mathbf{u}^*\right)=\left(x_1^*,x_2^*,u^*\right)=(-1.1994, -0.6243, 0)
Supongamos que en este caso nos interesa la primera solución. Entonces:
x1eq = double(sol.x1(1))
x2eq = double(sol.x2(1))
ueq = double(sol.u(1))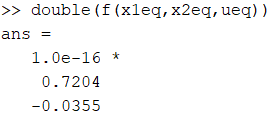\left(\mathbf{x}^*,\mathbf{u}^*\right)=\left(x_1^*,x_2^*,u^*\right)=(-1.1994, -0.6243, 0)
\Rightarrow \mathbf{f}\left(\mathbf{x}^*,\mathbf{u}^*\right)=\mathbf{0}
Jacobianos
El sistema no lineal
\begin{cases} \dot{\mathbf{x}}=\mathbf{f}\left(\mathbf{x}, \mathbf{u}\right) \\
\mathbf{y}=\mathbf{h}\left(\mathbf{x}\right) \end{cases}
tiene asociados tres jacobianos
D\mathbf{f}_\mathbf{x}\left(\mathbf{x},\mathbf{u}\right)=\dfrac{\partial \mathbf{f}\left(\mathbf{x},\mathbf{u}\right)}{\partial \mathbf{x}} \quad
D\mathbf{f}_\mathbf{u}\left(\mathbf{x},\mathbf{u}\right)=\dfrac{\partial \mathbf{f}\left(\mathbf{x},\mathbf{u}\right)}{\partial \mathbf{u}} \\
D\mathbf{h}_\mathbf{x}\left(\mathbf{x}\right)=\dfrac{d \mathbf{h}\left(\mathbf{x}\right)}{d \mathbf{x}}
Cada jacobiano es una matriz que puede ser complicada de calcular a mano, por lo que de nuevo acudimos a MATLAB.
Dfx(x1, x2, u) = jacobian(f, [x1, x2])
Dfu(x1, x2, u) = jacobian(f, u)
Dhx(x1, x2) = jacobian(h, [x1, x2])Nótese que los jacobianos aún son funciones de las variables de estado y las entradas.
Linealización local
Ya con el punto de equilibrio y los jacobianos finalmente puede obtenerse el modelo LTI como:
\begin{cases} \dot{\mathbf{z}}=\mathbf{A}\mathbf{z}+\mathbf{B}\mathbf{v} \\ \mathbf{w}=\mathbf{C}\mathbf{z} \\ \mathbf{z}(t_0)=\mathbf{z}_0 \end{cases}
\mathbf{A}=D\mathbf{f}_\mathbf{x}\left(\mathbf{x}^*,\mathbf{u}^*\right) \\
\mathbf{B}=D\mathbf{f}_\mathbf{u}\left(\mathbf{x}^*,\mathbf{u}^*\right) \\
\mathbf{C}=D\mathbf{h}_\mathbf{x}\left(\mathbf{x}^*\right)
Linealización local
bajo el cambio de variables:
\mathbf{z}=\delta\mathbf{x}=\mathbf{x}-\mathbf{x}^* \qquad \mathbf{z}_0=\delta\mathbf{x}^*\\
\mathbf{v}=\delta\mathbf{u}=\mathbf{u}-\mathbf{u}^* \\
\mathbf{w}=\delta\mathbf{y}=\mathbf{y}-\mathbf{h}\left(\mathbf{x}^*\right)
Linealización local
bajo el cambio de variables:
\mathbf{z}=\delta\mathbf{x}=\mathbf{x}-\mathbf{x}^* \qquad \mathbf{z}_0=\delta\mathbf{x}^*\\
\mathbf{v}=\delta\mathbf{u}=\mathbf{u}-\mathbf{u}^* \\
\mathbf{w}=\delta\mathbf{y}=\mathbf{y}-\mathbf{h}\left(\mathbf{x}^*\right)
desviación inicial con respecto del punto de equilibrio
\approx \mathbf{0}
Linealización local
bajo el cambio de variables
\mathbf{z}=\delta\mathbf{x}=\mathbf{x}-\mathbf{x}^* \qquad \mathbf{z}_0=\delta\mathbf{x}^*\\
\mathbf{v}=\delta\mathbf{u}=\mathbf{u}-\mathbf{u}^* \\
\mathbf{w}=\delta\mathbf{y}=\mathbf{y}-\mathbf{h}\left(\mathbf{x}^*\right)
desviación inicial con respecto del punto de equilibrio
El modelo LTI resultante se conoce como la linealización local del sistema no lineal alrededor del punto de equilibrio.
Con esto, puede encontrarse la linealización del modelo FitzHugh–Nagumo alrededor del primer punto de equilibrio como:
A = double( Dfx(x1eq, x2eq, ueq) )
B = double( Dfu(x1eq, x2eq, ueq) )
C = double( Dhx(x1eq, x2eq) )
% Sistema linealizado
sys_lin = ss(A, B, C, [])con esto entonces puede encontrarse la linealización del modelo FitzHugh–Nagumo alrededor del primer punto de equilibrio como
A = double( Dfx(x1eq, x2eq, ueq) )
B = double( Dfu(x1eq, x2eq, ueq) )
C = double( Dhx(x1eq, x2eq) )
% Sistema linealizado
sys_lin = ss(A, B, C, [])OJO: este modelo LTI está definido sobre las nuevas variables \(\mathbf{z},\mathbf{v}, \mathbf{w}\), por lo que debe emplearse el cambio de variables para ir hacia y regresar desde las variables originales \(\mathbf{x},\mathbf{u}, \mathbf{y}\) según se requiera.
Por ejemplo, supongamos que se empleó el sistema linealizado junto con LQR para diseñar un controlador (sólo para estabilizar) y se obtuvo:
\mathbf{K}=\begin{bmatrix} k_1 & k_2 \end{bmatrix}=\begin{bmatrix} 0.1080 & -0.0258 \end{bmatrix}
Entonces, el control está dado en las nuevas variables:
v=-\mathbf{K}\mathbf{z}=-0.1080z_1 -0.0258z_2
Para poder implementar el controlador en el sistema original debe emplearse el cambio de variables:
\mathbf{z}=\begin{bmatrix}z_1 \\ z_2 \end{bmatrix}=\mathbf{x}-\mathbf{x}^*=\begin{bmatrix} x_1-(-1.1994) \\ x_2-(-0.6243) \end{bmatrix} \\
\mathbf{v}=v=\mathbf{u}-\mathbf{u}^*=u-0
\begin{matrix} z_1=x_1+1.1994 \\ z_2=x_2+0.6243 \\ v = u\end{matrix}
\Rightarrow
Puede seguirse una lógica similar para la implementación e interpretación de observadores de estado.
v=-0.1080z_1 -0.0258z_2 \\
u=-0.1080(x_1+1.1994) -0.0258(x_2+0.6243)
puede seguirse una lógica similar para la implementación e interpretación de observadores de estado
v=-0.1080z_1 -0.0258z_2 \\
u=-0.1080(x_1+1.1994) -0.0258(x_2+0.6243)
IMPORTANTE: Simulink se encarga de todos estos detalles al emplear su herramienta de Model Linearizer. El modelo que retorna está dado en las nuevas variables y puede encontrarse el punto de equilibrio empleado dentro del objeto que contiene el modelo.
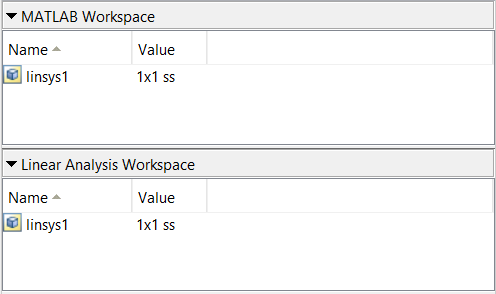
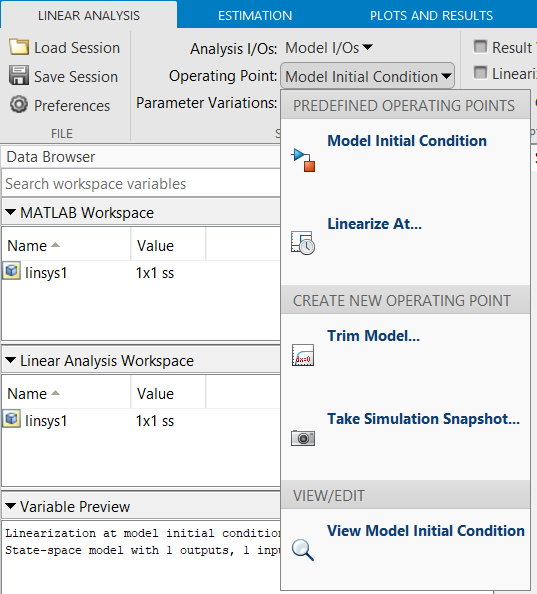
para encontrar puntos de equilibrio
BE3024 - Lecture 13 (2024)
By Miguel Enrique Zea Arenales
