Lección 3: Modelado de sistemas lineales de parámetro concentrado
BE3024 - Sistemas de Control 1 (Biomédica)
2do ciclo, 2024
¿Por qué?
Sistemas de parámetro concentrado
Elementos (lineales) básicos
+
Leyes fundamentales
Circuitos eléctricos lineales
Leyes de Kirchhoff
malla∑vi=0
\displaystyle\sum_{\textrm{malla}}v_i = 0
nodo∑ij=0
\displaystyle\sum_{\textrm{nodo}}i_j = 0
¿Cuál es el modelo del sistema?
G(s)=V(s)VC(s)
G(s)=\dfrac{V_C(s)}{V(s)}
(LCs2+RCs+1)VC(s)=V(s)
\left(LCs^2+RCs+1\right)V_C(s)=V(s)
G(s)=V(s)VC(s)=s2+(R/L)s+1/LC1/LC
G(s)=\dfrac{V_C(s)}{V(s)}=\dfrac{1/LC}{s^2+(R/L)s+1/LC}
(Ls+R+1/Cs)CsVC(s)=V(s)
\left(Ls+R+1/Cs\right)CsV_C(s)=V(s)
I(s)=IC(s)
I(s)=I_C(s)
Z(s)
Z(s)
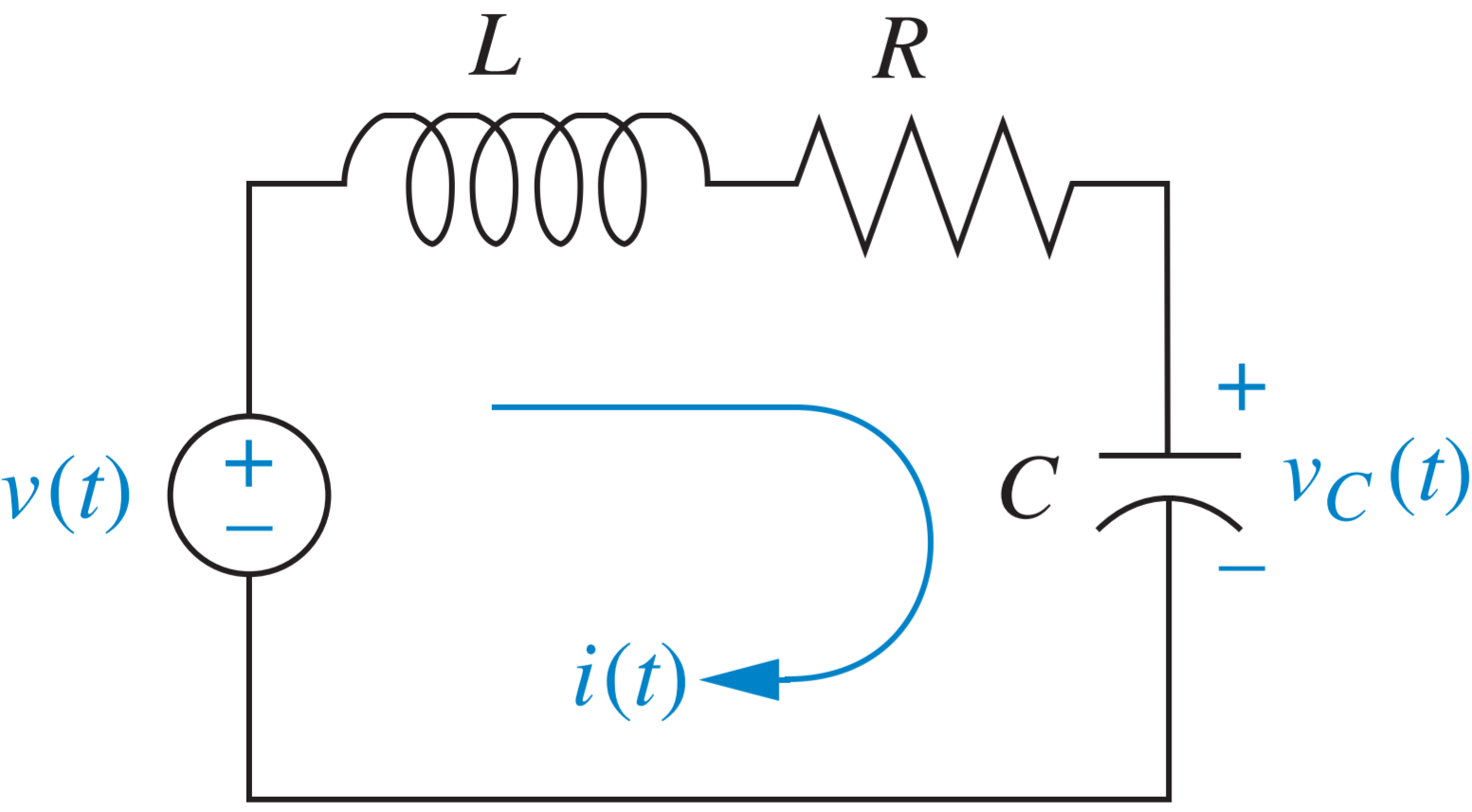
impedancia
>> clase3_circuitorlc.m
Método de impedancias para mallas
Válido para M mallas mi, aunque se presenta M=2 como ejemplo
m1:(m1∑Z(s))I1(s)−(m1 y m2∑Z(s))I2(s)=m1∑V(s)
m_1: \quad \left(\displaystyle\sum_{m_1}Z(s)\right)I_1(s)-\left(\displaystyle\sum_{m_1 \text{ y } m_2}Z(s)\right)I_2(s)=\displaystyle\sum_{m_1}V(s)
m2:(m2∑Z(s))I2(s)−(m2 y m1∑Z(s))I1(s)=m2∑V(s)
m_2: \quad \left(\displaystyle\sum_{m_2}Z(s)\right)I_2(s)-\left(\displaystyle\sum_{m_2 \text{ y } m_1}Z(s)\right)I_1(s)=\displaystyle\sum_{m_2}V(s)
Método de admitancias para nodos
Válido para N nodos ni, aunque se presenta N=2 como ejemplo
n1:(n1∑Y(s))V1(s)−(n1 y n2∑Y(s))V2(s)=n1∑I(s)
n_1: \quad \left(\displaystyle\sum_{n_1}Y(s)\right)V_1(s)-\left(\displaystyle\sum_{n_1 \text{ y } n_2}Y(s)\right)V_2(s)=\displaystyle\sum_{n_1}I(s)
n2:(n2∑Y(s))V2(s)−(n2 y n1∑Y(s))V1(s)=n2∑I(s)
n_2: \quad \left(\displaystyle\sum_{n_2}Y(s)\right)V_2(s)-\left(\displaystyle\sum_{n_2 \text{ y } n_1}Y(s)\right)V_1(s)=\displaystyle\sum_{n_2}I(s)
Plantee con ambos métodos
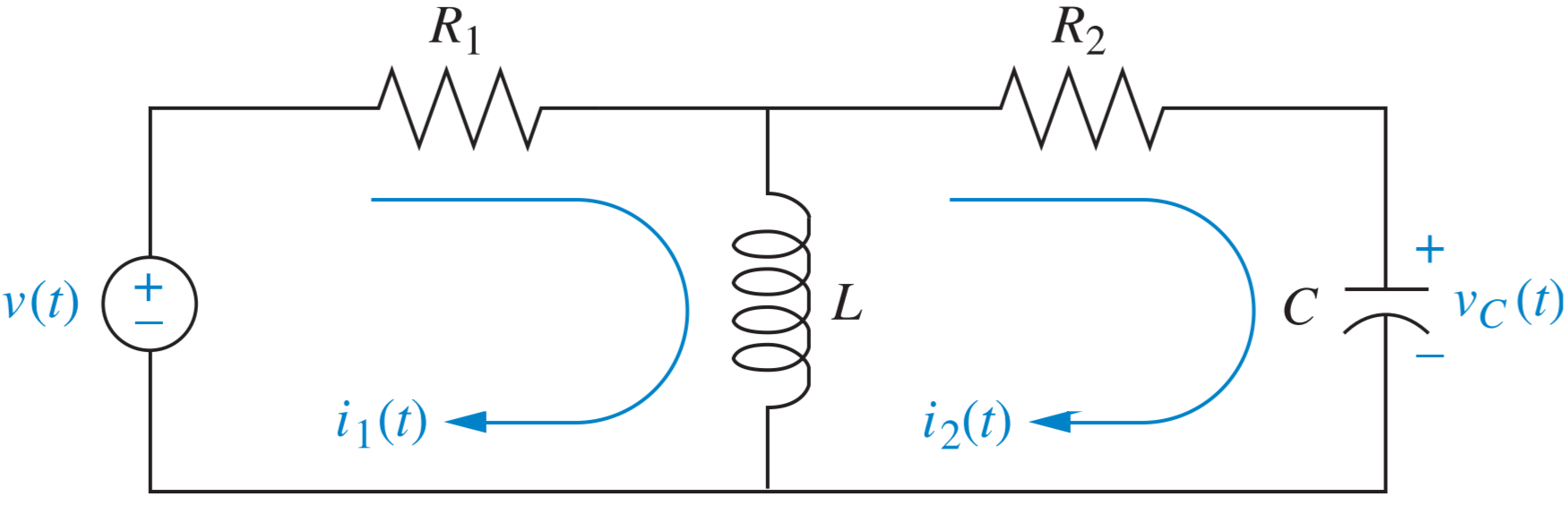
Puede profundizarse en los métodos de impedancias y admitancias en la sección 2.4 del libro de Nise
Sistemas mecánicos traslacionales
i∑fi=Mx¨
\displaystyle\sum_{i}f_i = M\ddot{x}
Segunda Ley de Newton
¿Cuál es el modelo del sistema?
G(s)=F(s)X(s)
G(s)=\dfrac{X(s)}{F(s)}
f(t)
f(t)
M
M
K
K
fv
f_v
x(t)
x(t)
(Ms2+fvs+K)X(s)=F(s)
\left(Ms^2+f_vs+K\right)X(s)=F(s)
G(s)=F(s)X(s)=Ms2+fvs+K1
G(s)=\dfrac{X(s)}{F(s)}=\dfrac{1}{Ms^2+f_vs+K}
v=iR⇒V(s)=I(s)Z(s)
v=iR \qquad \Rightarrow V(s)=I(s)Z(s)
(Ms2+fvs+K)X(s)=F(s)
\left(Ms^2+f_vs+K\right)X(s)=F(s)
G(s)=F(s)X(s)=Ms2+fvs+K1
G(s)=\dfrac{X(s)}{F(s)}=\dfrac{1}{Ms^2+f_vs+K}
v=iR⇒V(s)=I(s)Z(s)
v=iR \qquad \Rightarrow V(s)=I(s)Z(s)
impedancia mecánica ZM
Método de impedancias mecánicas
Válido para N masas, aunque se presenta N=2 como ejemplo
M1:(x1∑ZM(s))X1(s)−(x1 y x2∑ZM(s))X2(s)=x1∑F(s)
M_1: \quad \left(\displaystyle\sum_{x_1}Z_M(s)\right)X_1(s)-\left(\displaystyle\sum_{x_1 \text{ y } x_2}Z_M(s)\right)X_2(s)=\displaystyle\sum_{x_1}F(s)
M2:(x2∑ZM(s))X2(s)−(x2 y x1∑ZM(s))X1(s)=x2∑F(s)
M_2: \quad \left(\displaystyle\sum_{x_2}Z_M(s)\right)X_2(s)-\left(\displaystyle\sum_{x_2 \text{ y } x_1}Z_M(s)\right)X_1(s)=\displaystyle\sum_{x_2}F(s)
Aplique el método de impedancias
f(t)
f(t)
M1
M_1
K1
K_1
fv3
f_{v_3}
x1
x_1
M2
M_2
M3
M_3
x2
x_2
x3
x_3
K2
K_2
fv4
f_{v_4}
fv1
f_{v_1}
fv2
f_{v_2}
(K1+K2+fv1s+fv3s+M1s2)X1(s)−(K2)X2(s)−(fv3s)X3(s)=0
\left(K_1+K_2+f_{v_1}s+f_{v_3}s+M_1s^2\right)X_1(s)-\left(K_2\right)X_2(s)-\left(f_{v_3}s\right)X_3(s)=0
M1:
M_1:
(K2+fv2s+fv4s+M2s2)X2(s)−(K2)X1(s)−(fv4s)X3(s)=F(s)
\left(K_2+f_{v_2}s+f_{v_4}s+M_2s^2\right)X_2(s)-\left(K_2\right)X_1(s)-\left(f_{v_4}s\right)X_3(s)=F(s)
(fv3s+fv4s+M3s2)X3(s)−(fv3s)X1(s)−(fv4s)X2(s)=0
\left(f_{v_3}s+f_{v_4}s+M_3s^2\right)X_3(s)-\left(f_{v_3}s\right)X_1(s)-\left(f_{v_4}s\right)X_2(s)=0
M2:
M_2:
M3:
M_3:
1/4 de la masa del automóvil
M1
M_1
M2
M_2
K1
K_1
K2
K_2
fv
f_v
f
f
x1
x_1
x2
x_2
suspensión
rueda
llanta
superficie del camino
¿G(s)=F(s)X2(s)?
¿G(s)=\dfrac{X_2(s)}{F(s)}?
modelo de 1/4 de carro
X2(s)=G2(s)X1(s)
X_2(s)=G_2(s)X_1(s)
X1(s)=G3(s)X2(s)+G1(s)F(s)
X_1(s)=G_3(s)X_2(s)+G_1(s)F(s)
M2s2+fvs+K1fvs+K1
\dfrac{f_vs+K_1}{M_2s^2+f_vs+K_1}
M1s2+fvs+K1+K2fvs+K1
\dfrac{f_vs+K_1}{M_1s^2+f_vs+K_1+K_2}
M1s2+fvs+K1+K21
\dfrac{1}{M_1s^2+f_vs+K_1+K_2}
X1
X_1
F
F
X2
X_2
+
+
G3
G_3
G1
G_1
G2
G_2
>> clase3_suspension.m
X1
X_1
F
F
X2
X_2
+
+
G3
G_3
G1
G_1
G2
G_2
>> clase3_suspension.m
¿Qué ocurrió con la gravedad?
Ejercicio
Aplique el método de impedancias
f
f
1 kg
1 \text{ kg}
1 kg
1 \text{ kg}
1 N/m
1 \text{ N/m}
1 N-s/m
1 \text{ N-s/m}
Lección 3: Modelado de sistemas lineales de parámetro concentrado BE3024 - Sistemas de Control 1 (Biomédica) 2do ciclo, 2024
BE3024 - Lecture 3 (2024)
By Miguel Enrique Zea Arenales
BE3024 - Lecture 3 (2024)
- 181
