Marcos de referencia y transformaciones homogéneas
BE3027 - Robótica Médica
¿Por qué?
diversos agentes \(\Rightarrow\) diversas perspectivas
interacción e intercambio de información
lenguaje estándar y sistemático
\(\Rightarrow\) Álgebra lineal
diversos agentes \(\Rightarrow\) diversas perspectivas
interacción e intercambio de información
lenguaje estándar y sistemático
Cuerpos rígidos
\text{rigidez } \Rightarrow d(p_i,p_j)=\mathrm{cte.}
y
x
z
y
x
z
\hat{\mathbf{y}}_B
\hat{\mathbf{x}}_B
\hat{\mathbf{z}}_B
\left\{B\right\}
\hat{\mathbf{y}}_B
\hat{\mathbf{x}}_B
\hat{\mathbf{z}}_B
\left\{B\right\}
\hat{\mathbf{y}}_B
\hat{\mathbf{x}}_B
\hat{\mathbf{z}}_B
\left\{B\right\}
\boldsymbol{=}
y
x
z
\left\{I\right\}
\hat{\mathbf{y}}_B
\hat{\mathbf{x}}_B
\hat{\mathbf{z}}_B
\left\{B\right\}
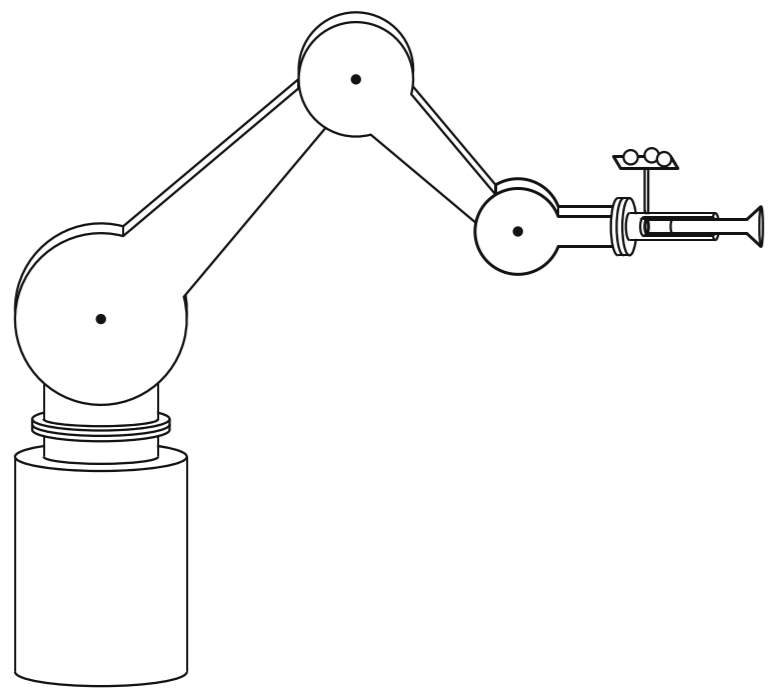
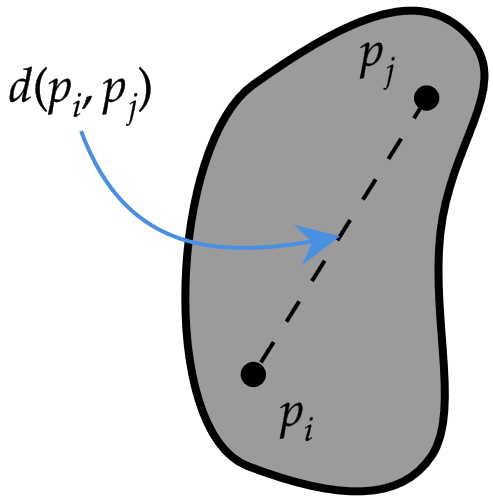
Marcos de referencia
marco inercial
body frame
Marcos de referencia
y
x
z
\left\{I\right\}
\hat{\mathbf{y}}_B
\hat{\mathbf{x}}_B
\hat{\mathbf{z}}_B
\left\{B\right\}
marco inercial
body frame
vectores en \(\{B\}\) forman un espacio vectorial
\(\hat{\mathbf{x}}_B, \hat{\mathbf{y}}_B, \hat{\mathbf{z}}_B\) base ortonormal para este espacio
Emplearemos marcos de referencia para ubicar cuerpos rígidos, describir su interacción y permitir el intercambio de información
y
x
z
\left\{I\right\}
\hat{\mathbf{y}}_B
\hat{\mathbf{x}}_B
\hat{\mathbf{z}}_B
\left\{B\right\}
p
y
x
z
\left\{I\right\}
\hat{\mathbf{y}}_B
\hat{\mathbf{x}}_B
\hat{\mathbf{z}}_B
\left\{B\right\}
{^B}\mathbf{p}
p
{^M}\mathbf{x}
nombre del vector
y
x
z
\left\{I\right\}
\hat{\mathbf{y}}_B
\hat{\mathbf{x}}_B
\hat{\mathbf{z}}_B
\left\{B\right\}
{^B}\mathbf{p}
p
{^M}\mathbf{x}
marco de referencia en donde se define
y
x
z
\left\{I\right\}
\hat{\mathbf{y}}_B
\hat{\mathbf{x}}_B
\hat{\mathbf{z}}_B
\left\{B\right\}
{^B}\mathbf{p}
p
{^I}\mathbf{p}
{^B}\mathbf{p}
{^I}\mathbf{p}
distintos espacios vectoriales
\equiv
y
x
z
\left\{I\right\}
\hat{\mathbf{y}}_B
\hat{\mathbf{x}}_B
\hat{\mathbf{z}}_B
\left\{B\right\}
{^B}\mathbf{p}
p
{^I}\mathbf{p}
{^I}\mathcal{T}_B
debe existir para transformar de un espacio al otro
\mathcal{T}
{^I}\mathcal{T}_B
marco destino
marco fuente
cuerpos rígidos \(\equiv\) transformaciones rígidas
{^I}\mathbf{p}={^I}\mathcal{T}_B\left\{{^B}\mathbf{p}\right\}
{^I}\mathbf{p}={^I}\mathcal{T}_B\left\{{^B}\mathbf{p}\right\}
x_R
y_R
z_R
\{R\}
x_S
y_S
z_S
\{S\}
x_C
y_C
z_C
\{C\}
x_N
z_N
y_N
\{N\}
p
x_R
y_R
z_R
\{R\}
x_S
y_S
z_S
\{S\}
x_C
y_C
z_C
\{C\}
x_N
z_N
y_N
\{N\}
p
{^C}\mathbf{p}
{^S}\mathbf{p}
x_R
y_R
z_R
\{R\}
x_S
y_S
z_S
\{S\}
x_C
y_C
z_C
\{C\}
x_N
z_N
y_N
\{N\}
p
{^C}\mathbf{p}
{^S}\mathbf{p}
{^R}\mathcal{T}_S
{^N}\mathcal{T}_S
{^N}\mathcal{T}_C
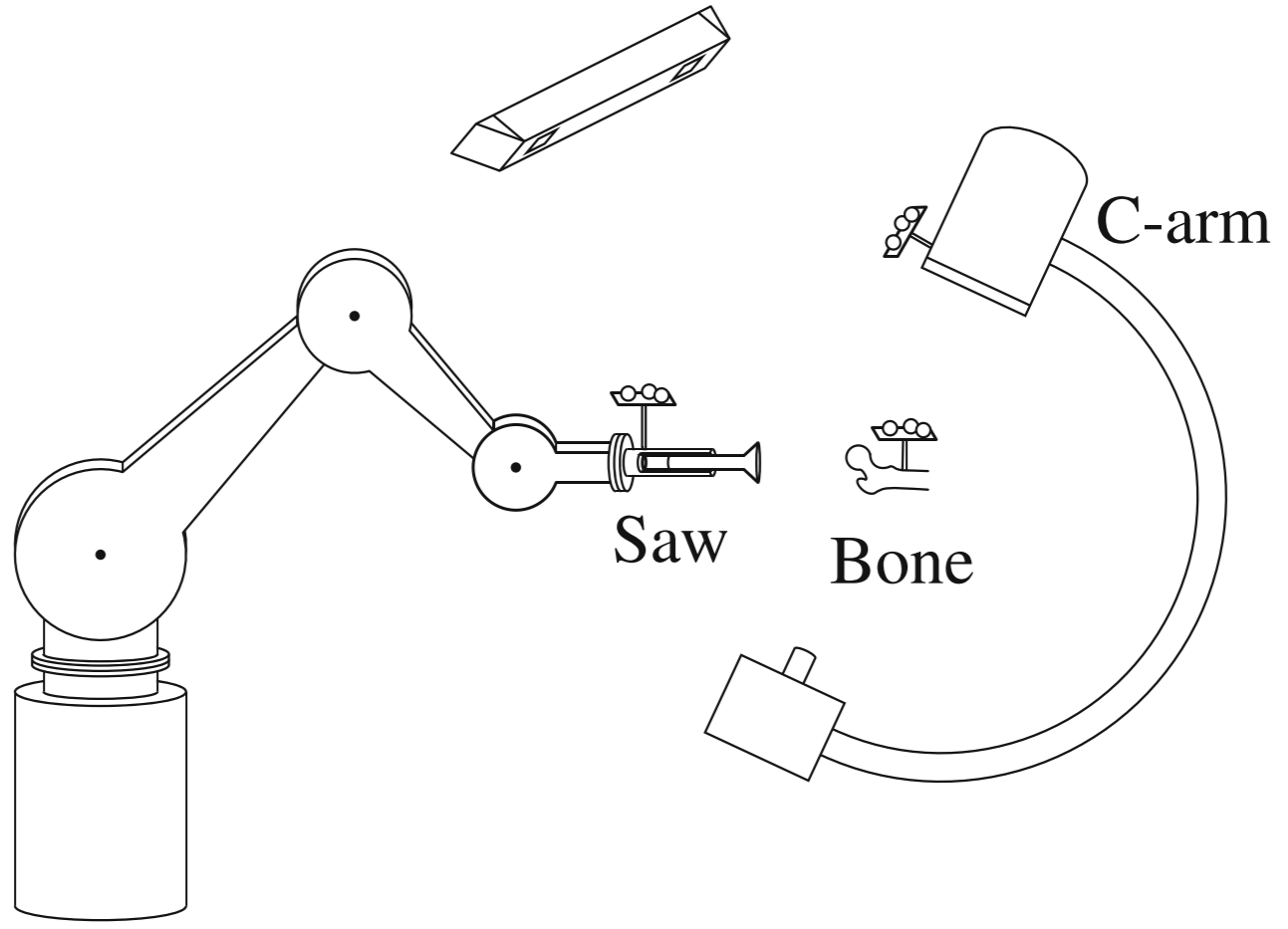
¿Posición del hueso con respecto al sistema de navegación?
¿Posición del hueso con respecto a la base del robot?
Matriz de transformación homogénea
{^I}\mathcal{T}_B \sim {^I}\mathbf{T}_B
toda transformación lineal tiene asociada una matriz
Pose = posición + orientación
{^I}\mathbf{T}_B
pose de \(\{B\}\) con respecto de \(\{I\}\)
la matriz como tal también posee información
x_R
y_R
z_R
\{R\}
x_S
y_S
z_S
\{S\}
x_C
y_C
z_C
\{C\}
x_N
z_N
y_N
\{N\}
p
{^C}\mathbf{p}
{^S}\mathbf{p}
{^R}\mathcal{T}_S
{^N}\mathcal{T}_S
{^N}\mathcal{T}_C
¿Ubicación de la base del robot con respecto al sistema de navegación?
¿Pose (posición + orientación) de la sierra con respecto del brazo en C?
BE3027 - Lecture 1 (2024)
By Miguel Enrique Zea Arenales
