Representaciones para la orientación en 3D
BE3027 - Robótica Médica
¿Por qué?
\{A\}
x_A
y_A
z_A
x_B
y_B
z_B
\{B\}
\{A\}
x_A
y_A
z_A
x_B
y_B
z_B
\{B\}
\{A\}
x_A
y_A
z_A
x_B
y_B
z_B
\{B\}
traslaciones
rotaciones
\{A\}
x_A
y_A
z_A
x_B
y_B
z_B
\{B\}
\{A\}
x_A
y_A
z_A
x_B
y_B
z_B
\{B\}
\{A\}
x_A
y_A
z_A
x_B
y_B
z_B
\{B\}
para determinar
{^I}\mathbf{T}_B=\begin{bmatrix} r_{11} & r_{12} & r_{13} & x \\
r_{21} & r_{22} & r_{23} & y \\
r_{31} & r_{32} & r_{33} & z \\
0 & 0 & 0 & 1 \end{bmatrix}
{^I}\mathbf{R}_B
{^I}\mathbf{o}_B
matriz de rotación
vector de traslación
Sin embargo, aunque podemos obtener el valor de \({^I}\mathbf{R}_B\) aún no podemos interpretarla.
¿Por qué es importante esto?
El teorema de rotación de Euler
Primera interpretación
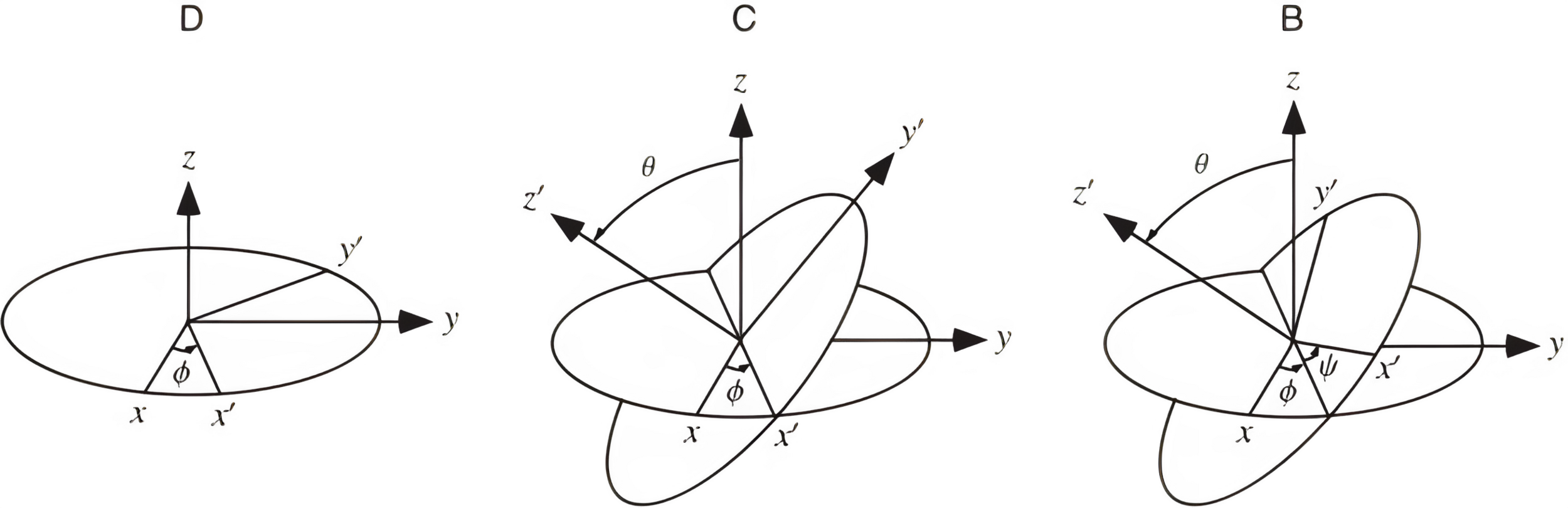
ángulos de Euler
\mathbf{R}_x(\theta)=\begin{bmatrix} 1 & 0 & 0 \\ 0 & \cos\theta & -\sin\theta \\ 0 & \sin\theta & \cos\theta \end{bmatrix}
\mathbf{R}_y(\theta)=\begin{bmatrix} \cos\theta & 0 & \sin\theta \\ 0 & 1 & 0 \\ -\sin\theta & 0 & \cos\theta \end{bmatrix}
\mathbf{R}_z(\theta)=\begin{bmatrix} \cos\theta & -\sin\theta & 0 \\ \sin\theta & \cos\theta & 0 \\ 0 & 0 & 1 \end{bmatrix}
Rx = rotx(theta)Ry = roty(theta)Rz = rotz(theta)12 posibles secuencias
Euler (se repite un eje): XYX, XZX, YXY, YZY, ZXZ, ZYZ.
Cardán (no se repiten ejes): XYZ, XZY, YZX, YXZ, ZXY, ZYX.
(\psi)
z
x
y
(\theta)
(\phi)
ZYX | XYZ
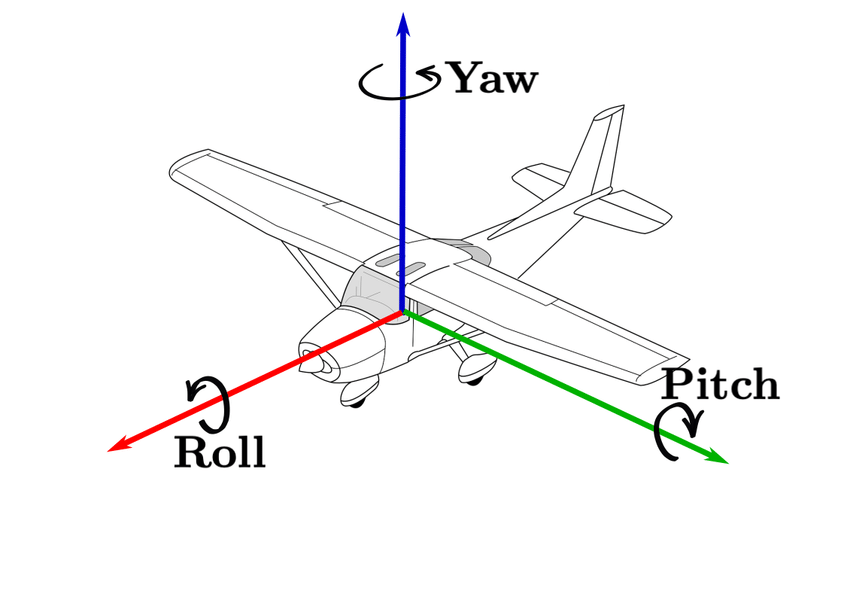
ángulos de navegación
(Tait-Bryan)
Ejemplo
Los sensores de un avión retornaron que la pose actual del mismo \(\{B\}\) con respecto del marco de despegue \(\{A\}\) es
¿Cuál es el roll, pitch y yaw del avión?
>> be3027_clase3_angulos_euler.mlx
{^A}\mathbf{T}_B=\begin{bmatrix} 0.3536 & 0.7071 & 0.6124 & 500.0000 \\ 0.1268 & 0.6124 & -0.7803 & -700.0000 \\ -0.9268 & 0.3536 & 0.1268 & 800.0000 \\ 0 & 0 & 0 & 1 \end{bmatrix}
Limitantes
singularidades y el gimbal lock
Segunda interpretación
eje-ángulo
cuaterniones unitarios
Representación eje-ángulo
% Robotics System Toolbox
w = rotm2axang(R)
R = axang2rotm(w)\hat{\boldsymbol{\omega}}
\theta
vector unitario del eje de rotación
magnitud de la rotación
Representación eje-ángulo
\hat{\boldsymbol{\omega}}
\theta
vector unitario del eje de rotación
magnitud de la rotación
% Robotics Toolbox
[theta, w_hat] = tr2angvec(T)
[theta, w_hat] = tr2angvec(R)
T = angvec2tr(theta, w_hat)
R = angvec2r(theta, w_hat)Representación eje-ángulo
\hat{\boldsymbol{\omega}}
\theta
vector unitario del eje de rotación
magnitud de la rotación
% Robotics Toolbox
[theta, w_hat] = tr2angvec(T)
[theta, w_hat] = tr2angvec(R)
T = angvec2tr(theta, w_hat)
R = angvec2r(theta, w_hat)¿Limitantes? debe transformarse a matrices de rotación para realizar operaciones
Cuaterniones unitarios
Cuaterniones unitarios
% Robotics Toolbox
Q = UnitQuaternion(T)
Q = UnitQuaternion(R)
T = Q.T
R = Q.R\mathcal{Q}=\{\eta,\boldsymbol{\epsilon}\}=\begin{bmatrix} \eta \\ \boldsymbol{\epsilon} \end{bmatrix}=
\begin{bmatrix} \cos(\theta/2) \\ \hat{\boldsymbol{\omega}}\sin(\theta/2) \end{bmatrix} \quad
\begin{matrix} \eta\in\mathbb{R} \\ \boldsymbol{\epsilon}\in\mathbb{R}^3 \end{matrix}
\eta^2+\boldsymbol{\epsilon}^\top\boldsymbol{\epsilon}=1
norma unitaria
Cuaterniones unitarios
% Robotics System Toolbox
Q = rotm2quat(R)
R = quat2rotm(Q)\mathcal{Q}=\{\eta,\boldsymbol{\epsilon}\}=\begin{bmatrix} \eta \\ \boldsymbol{\epsilon} \end{bmatrix}=
\begin{bmatrix} \cos(\theta/2) \\ \hat{\boldsymbol{\omega}}\sin(\theta/2) \end{bmatrix} \quad
\begin{matrix} \eta\in\mathbb{R} \\ \boldsymbol{\epsilon}\in\mathbb{R}^3 \end{matrix}
\eta^2+\boldsymbol{\epsilon}^\top\boldsymbol{\epsilon}=1
norma unitaria
Cuaterniones unitarios
% Robotics System Toolbox
Q = rotm2quat(R)
R = quat2rotm(Q)\mathcal{Q}=\{\eta,\boldsymbol{\epsilon}\}=\begin{bmatrix} \eta \\ \boldsymbol{\epsilon} \end{bmatrix}=
\begin{bmatrix} \cos(\theta/2) \\ \hat{\boldsymbol{\omega}}\sin(\theta/2) \end{bmatrix} \quad
\begin{matrix} \eta\in\mathbb{R} \\ \boldsymbol{\epsilon}\in\mathbb{R}^3 \end{matrix}
\eta^2+\boldsymbol{\epsilon}^\top\boldsymbol{\epsilon}=1
norma unitaria
los cuaterniones unitarios sí pueden operarse (eficientemente) sin tener que transformase a matrices de rotación
\mathcal{Q}_3=\mathcal{Q}_1 * \mathcal{Q}_2= \{\eta_1, \boldsymbol{\epsilon}_1\} * \{\eta_2, \boldsymbol{\epsilon}_2\} \newline
\mathcal{Q}_3=\{ \eta_1\eta_2-\boldsymbol{\epsilon}_1^\top\boldsymbol{\epsilon}_2, \eta_1\boldsymbol{\epsilon}_2+\eta_2\boldsymbol{\epsilon}_1+\boldsymbol{\epsilon}_1 \times \boldsymbol{\epsilon}_2\}
si se tiene que \( \mathcal{Q}_1 \sim \mathbf{R}_1, \ \mathcal{Q}_2 \sim \mathbf{R}_2\) y \( \mathcal{Q}_3 \sim \mathbf{R}_3=\mathbf{R}_1\mathbf{R}_2\) entonces
\mathcal{Q}_1^{-1}=\{\eta_1, -\boldsymbol{\epsilon}_1\} \sim \mathbf{R}_1^{-1}=\mathbf{R}_1^\top
\mathbf{w}=\mathbf{R}_1\mathbf{v}\equiv \{0, \mathbf{w}\}= \mathcal{Q}_1*\{0,\mathbf{v}\}*\mathcal{Q}_1^{-1}
\mathcal{Q}_3=\mathcal{Q}_1 * \mathcal{Q}_2= \{\eta_1, \boldsymbol{\epsilon}_1\} * \{\eta_2, \boldsymbol{\epsilon}_2\} \newline
\mathcal{Q}_3=\{ \eta_1\eta_2-\boldsymbol{\epsilon}_1^\top\boldsymbol{\epsilon}_2, \eta_1\boldsymbol{\epsilon}_2+\eta_2\boldsymbol{\epsilon}_1+\boldsymbol{\epsilon}_1 \times \boldsymbol{\epsilon}_2\}
si se tiene que \( \mathcal{Q}_1 \sim \mathbf{R}_1, \ \mathcal{Q}_2 \sim \mathbf{R}_2\) y \( \mathcal{Q}_3 \sim \mathbf{R}_3=\mathbf{R}_1\mathbf{R}_2\) entonces
\mathcal{Q}_1^{-1}=\{\eta_1, -\boldsymbol{\epsilon}_1\} \sim \mathbf{R}_1^{-1}=\mathbf{R}_1^\top
\mathbf{w}=\mathbf{R}_1\mathbf{v}\equiv \{0, \mathbf{w}\}= \mathcal{Q}_1*\{0,\mathbf{v}\}*\mathcal{Q}_1^{-1}
¿Limitantes? los cuaterniones pierden toda interpretación intuitiva
BE3027 - Lecture 3 (2024)
By Miguel Enrique Zea Arenales
