Diseño de compensadores empleando el Root Locus
IE3036 - Sistemas de Control 1
Ejercicio 1
esboce el Root Locus
(sin MATLAB)
\mathrm{Im}(s)
\mathrm{Re}(s)
Motivación
\mathrm{Im}(s)
\mathrm{Re}(s)
Bajo esta intuición se propone lo siguiente
+
-
K
G(s)
H(s)
R(s)
Y(s)
D(s)
Bajo esta intuición se propone lo siguiente
+
-
K
G(s)
H(s)
R(s)
Y(s)
D(s)
\tilde{G}(s)
Bajo esta intuición se propone lo siguiente
+
-
K
G(s)
H(s)
R(s)
Y(s)
D(s)
\tilde{G}(s)
\(D(s)\) se combina con la planta para formar una "nueva planta" \(\tilde{G}(s)\) que presente un Root Locus deseado
se denomina compensador a \(D(s)\)
T(s)=\dfrac{Y(s)}{R(s)}=\dfrac{KG(s)D(s)}{1+KG(s)D(s)H(s)} \\
=\dfrac{K\tilde{G}(s)}{1+K\tilde{G}(s)H(s)}
NOTA: \(C(s)=KD(s)\)
generalidades para el diseño de compensadores
El añadir un cero en el LHP hala al Root Locus a la izquierda.
- mejora estabilidad.
- aumenta el asentamiento.
- hace más rápida la respuesta transiente.
- puede empeorar el \(e_{ss}\).
\mathrm{Im}(s)
\mathrm{Re}(s)
\mathrm{Im}(s)
\mathrm{Re}(s)
El añadir un polo en el LHP hala al Root Locus a la derecha.
- empeora estabilidad.
- disminuye el asentamiento.
- si el sistema en lazo cerrado es estable, el polo puede disminuir el \(e_{ss}\).
\mathrm{Im}(s)
\mathrm{Re}(s)
\mathrm{Im}(s)
\mathrm{Re}(s)
NO puede añadirse físicamente un cero sin un polo. Si quiere añadirse un cero por si sólo obligadamente debe añadirse un polo muy alejado al lado izquierdo para no deteriorar el efecto del cero agregado.
\dfrac{}{s+p}
D(s)=\dfrac{s+q}{}
NO es causal \(\Rightarrow\) NO puede implementarse
debe hacerse \(p\to\infty\) para que no afecte
se identifican dos tipos de mejora:
- mejora en respuesta estacionaria.
- mejora en respuesta transitoria.
- mejora en ambas.
se identifican dos tipos de mejora:
- mejora en respuesta estacionaria.
- mejora en respuesta transitoria.
- mejora en ambas.
>> clase10_compensadores_rootlocus.m
G(s)=\dfrac{1}{(s+1)(s+3)},
G(s)=\dfrac{1}{s^2+2s+2}
mejora en la respuesta estacionaria
D(s)=1
KD(s)=K=k_P
Control proporcional (puro)
\mathrm{Im}(s)
\mathrm{Re}(s)
D(s)=\dfrac{1}{T_Is}
KD(s)=\dfrac{K}{T_I}\dfrac{1}{s}=k_I\dfrac{1}{s}
Control integral (puro)
\mathrm{Im}(s)
\mathrm{Re}(s)
s=0
D(s)=1+\dfrac{1}{T_Is}
KD(s)=K+\dfrac{K}{T_I}\dfrac{1}{s}=k_P+k_I\dfrac{1}{s}
Control PI
\mathrm{Im}(s)
\mathrm{Re}(s)
s=-\dfrac{1}{T_I}
D(s)=\dfrac{s-q_0}{s-p_0}
Compensador Lag
s=p_0
|p_0|<|q_0|
s=q_0
\mathrm{Im}(s)
\mathrm{Re}(s)
\(\approx\) control PI pero sin los "problemas" de implementación
metodología de diseño:
- se coloca el polo bastante cerca del origen, ej: \(p_0=0.01\).
- se coloca el cero cerca del polo para "cancelarlo", ej: \(q_0=0.1\).
- el compensador disminuye el \(e_{ss}\) aunque hace más lento al sistema.
Paréntesis: tipos de error
\mathbf{1}(t)
t\mathbf{1}(t)
\dfrac{1}{2}t^2\mathbf{1}(t)
\dfrac{1}{1+K_p}
\dfrac{1}{1+K_p}
\dfrac{1}{K_v}
\dfrac{1}{K_a}
\dfrac{1}{K_a}
\dfrac{1}{K_v}
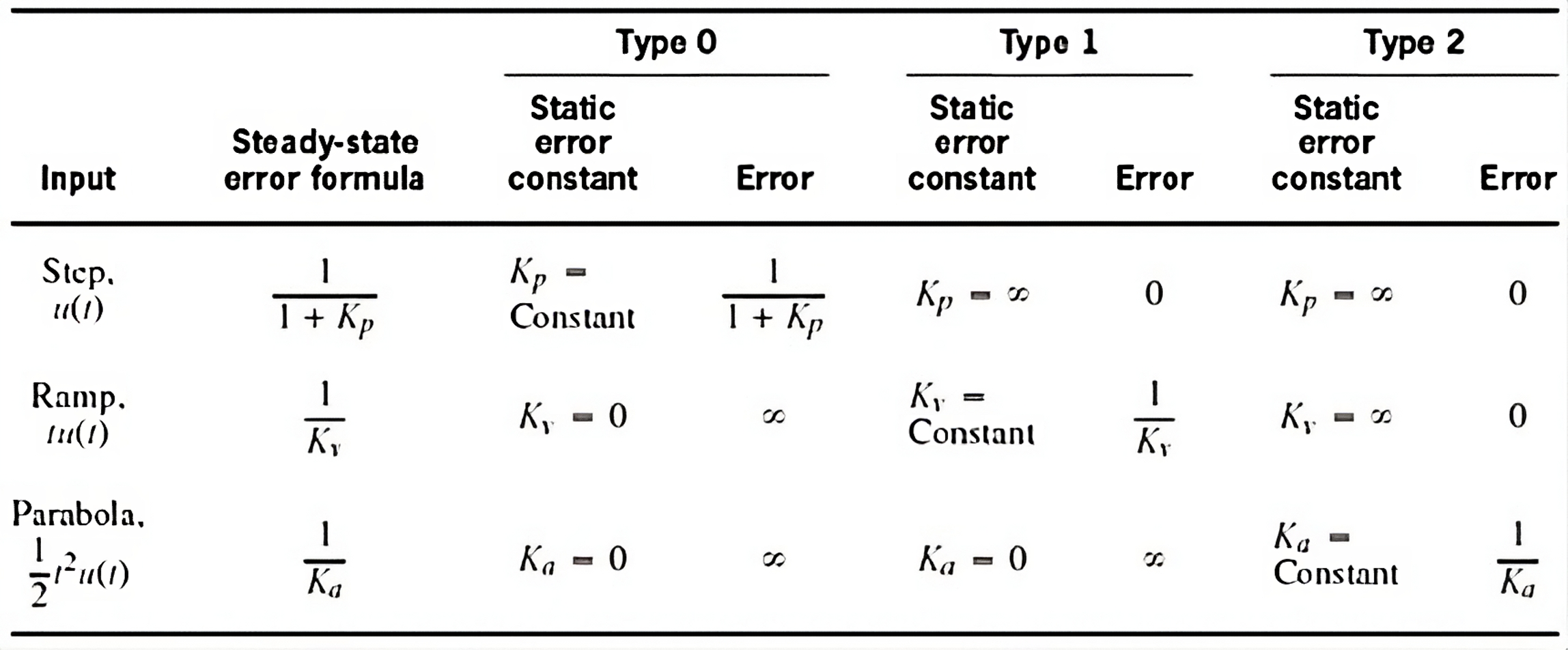
mejora en la respuesta transitoria
D(s)=1
KD(s)=K=k_P
Control proporcional (puro)
\mathrm{Im}(s)
\mathrm{Re}(s)
D(s)=T_Ds
KD(s)=K T_D s=k_D s
Control derivativo (puro)
\mathrm{Im}(s)
\mathrm{Re}(s)
s=0
D(s)=T_Ds
KD(s)=K T_D s=k_D s
Control derivativo (puro)
\mathrm{Im}(s)
\mathrm{Re}(s)
s=0
debe añadirse un polo para que sea implementable
D(s)=1+T_Ds
KD(s)=K+K T_D s=k_P+k_D s
Control PD
\mathrm{Im}(s)
\mathrm{Re}(s)
s=-\dfrac{1}{T_D}
D(s)=1+T_Ds
KD(s)=K+K T_D s=k_P+k_D s
Control PD
s=-\dfrac{1}{T_D}
\mathrm{Im}(s)
\mathrm{Re}(s)
debe añadirse un polo para que sea implementable
D(s)=\dfrac{s-q_0}{s-p_0}
Compensador Lead
s=q_0
|p_0|>|q_0|
s=p_0
\mathrm{Im}(s)
\mathrm{Re}(s)
\(\approx\) control PD pero sin los "problemas" de implementación
busca que el Root Locus pase por un punto deseado \(s=s_1\)
metodología de diseño I:
- se selecciona el cero \(q_0\) tal que cancele un polo real y estable de la planta.
- se encuentra \(K\) y \(p_0\) tal que \(1+L(s_1)=0\).
- ejemplo: compensador Lead para \(G(s)=\dfrac{1}{(s+1)(s+3)}, \quad s_1=-3+2\jmath.\)
metodología de diseño II: si no hay polo estable que cancelar
s_1=|s_1|e^{\jmath \beta} \\
L(s_1)=\left|L(s_1)\right|e^{\jmath \psi}
D(s)=\dfrac{a_1s+a_0}{b_1s+1}
a_0=\dfrac{\text{ganancia DC deseada para el sistema en lazo abierto}}{|L(0)|}
a_1=\dfrac{\sin(\beta)+a_0|L(s_1)|\sin(\beta-\psi)}{|s_1||L(s_1)|\sin(\beta)}
b_1=\dfrac{\sin(\beta+\psi)+a_0|L(s_1)|\sin(\beta)}{-|s_1|\sin(\psi)}
mejora en ambas respuestas
D(s)=1+\dfrac{1}{T_Is}+T_Ds
KD(s)=K++\dfrac{K}{T_I}\dfrac{1}{s}+K T_D s\\
=k_P+\dfrac{k_I}{s}+k_D s
Control PID
\mathrm{Im}(s)
\mathrm{Re}(s)
D(s)=1+\dfrac{1}{T_Is}+T_Ds
KD(s)=K++\dfrac{K}{T_I}\dfrac{1}{s}+K T_D s\\
=k_P+\dfrac{k_I}{s}+k_D s
Control PID
\mathrm{Im}(s)
\mathrm{Re}(s)
\dfrac{T_Ds}{\tau s+1}
de ser necesario
metodología empírica de diseño:
- se seleccionan \(T_I\) y \(T_D\) tal que representen la proporción de control integral y derivativo con respecto al proporcional.
- ej: P (100%), I (10%), D (1%) implican \(T_I=10\) y \(T_D=0.01\).
metodología "formal" de diseño:
s_1=|s_1|e^{\jmath \beta} \\
L(s_1)=\left|L(s_1)\right|e^{\jmath \psi}
k_P=-\dfrac{\sin(\beta+\psi)}{|L(s_1)|\sin(\beta)}-\dfrac{2 k_I\cos(\beta)}{|s_1|}
k_D=\dfrac{\sin(\psi)}{|s_1||L(s_1)|\sin(\beta)}+\dfrac{k_I}{|s_1|^2}
\(T_I\) para cumplir con cierto criterio de diseño, usualmente relacionado al \(e_{ss}\)
D(s)=D_\mathrm{Lag}(s)D_\mathrm{Lead}(s)
Compensador Lead-Lag
\mathrm{Im}(s)
\mathrm{Re}(s)
\(\approx\) control PID
sin ambigüedades de implementación
metodología de diseño:
- se diseña un compensador Lead \(D_\mathrm{Lead}(s)\) para cumplir con requerimientos de respuesta transitoria.
- se combina el compensador Lead con la planta para formar \(\tilde{G}(s)=D_\mathrm{Lead}(s)G(s)\).
- se diseña el compensador Lag \(D_\mathrm{Lag}(s)\) para planta combinada \(\tilde{G}(s)\).
IE3036 - Lecture 12 (2024) POR HACER
By Miguel Enrique Zea Arenales
