MT3006 - Robótica 2
Localización empleando odometría, sensores inerciales y sistemas de posicionamiento II
Completando el problema
plantear el problema de localización bajo la perspectiva del filtro de Kalman
predicción + corrección
propiocepción
exterocepción
estimación de pose
plantear el problema de localización bajo la perspectiva del filtro de Kalman
predicción + corrección
propiocepción
exterocepción
estimación de pose
Corrección de pose empleando mediciones exteroceptivas
GNSS en ambientes abiertos
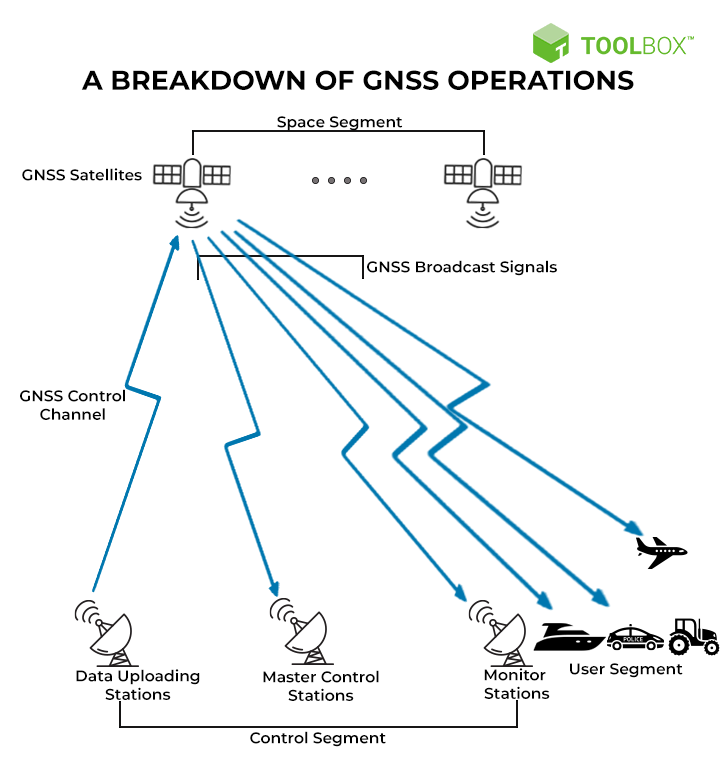
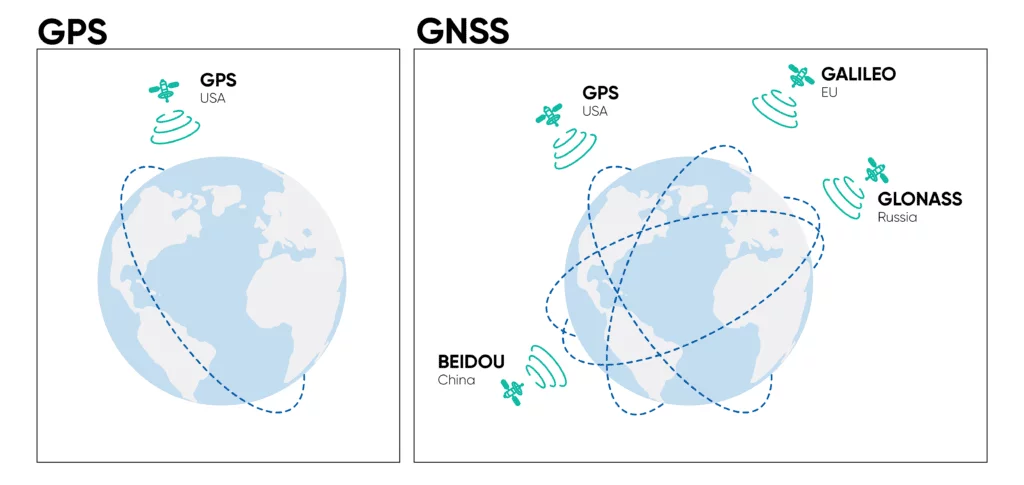
modelo de medición para un receptor GPS (GNSS)
\mathbf{y}_k=\mathbf{C}\mathbf{x}_k+\mathbf{v}_k=\mathbf{I}{^I}\mathbf{p}_k+\mathbf{v}_k
\mathbf{y}_k \equiv {^N}\mathbf{p}_k+\mathbf{v}_k
\mathbf{Q}_v=
\begin{bmatrix} \sigma_x^2 & 0 & 0 \\ 0 & \sigma_y^2 & 0 \\ 0 & 0 & \sigma_z^2 \end{bmatrix}
modelo de medición para un receptor GPS (GNSS)
\mathbf{y}_k=\mathbf{C}\mathbf{x}_k+\mathbf{v}_k=\mathbf{I}{^I}\mathbf{p}_k+\mathbf{v}_k
\sim \mathcal{N}\left(\mathbf{0},\mathbf{Q}_v\right)
\mathbf{y}_k \equiv {^N}\mathbf{p}_k+\mathbf{v}_k
\mathbf{Q}_v=
\begin{bmatrix} \sigma_x^2 & 0 & 0 \\ 0 & \sigma_y^2 & 0 \\ 0 & 0 & \sigma_z^2 \end{bmatrix}
modelo de medición para un receptor GPS (GNSS)
por lo general "grandes", pero el sensor presenta bias "perfecto"
\mathbf{y}_k=\mathbf{C}\mathbf{x}_k+\mathbf{v}_k=\mathbf{I}{^I}\mathbf{p}_k+\mathbf{v}_k
\sim \mathcal{N}\left(\mathbf{0},\mathbf{Q}_v\right)
\mathbf{y}_k \equiv {^N}\mathbf{p}_k+\mathbf{v}_k
Ejemplo: módulo FGPMMOPA6B
Ejemplo: módulo FGPMMOPA6B
¿GPS en espacios cerrados?
sistemas de captura de movimiento
óptico (ej. OptiTrack)
UWB (ej. DWM1000)
¿GPS en espacios cerrados?
mismo modelo de medición que para el GPS
óptico (ej. OptiTrack)
UWB (ej. DWM1000)
con varianzas mucho menores y también con capacidad de medir orientación completa (i.e. el mejor sensor posible*)
con varianzas menores al GPS pero mayores a sistemas ópticos y más accesibles*
Orientación empleando IMUs
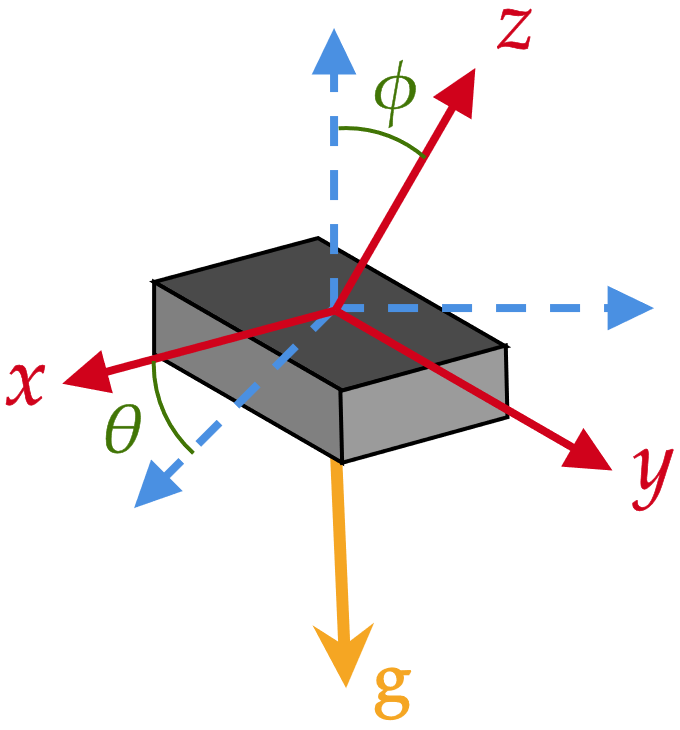
se hizo la predicción de orientación con los giroscopios
\begin{bmatrix} {^S}\dot{\boldsymbol{\theta}}_{NS} \\ {^S}\dot{\mathbf{b}}_g \end{bmatrix}=
\begin{bmatrix} \mathbf{0} & -\mathbf{I} \\ \mathbf{0} & \mathbf{0} \end{bmatrix} \begin{bmatrix} {^S}\boldsymbol{\theta}_{NS} \\ {^S}\mathbf{b}_{bg} \end{bmatrix}
+ \begin{bmatrix} \mathbf{I} \\ \mathbf{0} \end{bmatrix} \boldsymbol{\omega}_g
+ \begin{bmatrix} -{^S}\mathbf{n}_g \\ {^S}\mathbf{b}_{bg} \end{bmatrix}
\begin{bmatrix} \dot{\mathbf{q}} \\ {^S}\dot{\mathbf{b}}_g \end{bmatrix}=
\begin{bmatrix} \dfrac{1}{2}\boldsymbol{\Omega}\left( \boldsymbol{\omega}_g-{^S}\mathbf{b}_g-{^S}\mathbf{n}_g \right)\mathbf{q} \\
{^S}\mathbf{b}_{bg} \end{bmatrix}
Orientación empleando IMUs
se hizo la predicción de orientación con los giroscopios
\begin{bmatrix} {^S}\dot{\boldsymbol{\theta}}_{NS} \\ {^S}\dot{\mathbf{b}}_g \end{bmatrix}=
\begin{bmatrix} \mathbf{0} & -\mathbf{I} \\ \mathbf{0} & \mathbf{0} \end{bmatrix} \begin{bmatrix} {^S}\boldsymbol{\theta}_{NS} \\ {^S}\mathbf{b}_{bg} \end{bmatrix}
+ \begin{bmatrix} \mathbf{I} \\ \mathbf{0} \end{bmatrix} \boldsymbol{\omega}_g
+ \begin{bmatrix} -{^S}\mathbf{n}_g \\ {^S}\mathbf{b}_{bg} \end{bmatrix}
\begin{bmatrix} \dot{\mathbf{q}} \\ {^S}\dot{\mathbf{b}}_g \end{bmatrix}=
\begin{bmatrix} \dfrac{1}{2}\boldsymbol{\Omega}\left( \boldsymbol{\omega}_g-{^S}\mathbf{b}_g-{^S}\mathbf{n}_g \right)\mathbf{q} \\
{^S}\mathbf{b}_{bg} \end{bmatrix}
es una cantidad inercial, por lo que pueden obtenerse mediciones exteroceptivas
{^S}\mathbf{a}={^S}\mathbf{R}_N\left({^N}\mathbf{a}-{^N}\mathbf{g}\right)+{^S}\mathbf{b}_a+{^S}\mathbf{n}_a
si se asume que la gravedad predomina sobre la aceleración lineal* del cuerpo (sensor)
{^S}\mathbf{a}={^S}\mathbf{R}_N\left({^N}\mathbf{a}-{^N}\mathbf{g}\right)+{^S}\mathbf{b}_a+{^S}\mathbf{n}_a
{^S}\mathbf{a}=-{^S}\mathbf{R}_N {^N}\mathbf{g}+{^S}\mathbf{b}_a+{^S}\mathbf{e}_a
si se asume que la gravedad predomina sobre la aceleración lineal* del cuerpo (sensor)
{^S}\mathbf{a}={^S}\mathbf{R}_N\left({^N}\mathbf{a}-{^N}\mathbf{g}\right)+{^S}\mathbf{b}_a+{^S}\mathbf{n}_a
el nuevo "ruido" debe considerar también la incertidumbre del modelo
{^S}\mathbf{a}=-{^S}\mathbf{R}_N {^N}\mathbf{g}+{^S}\mathbf{b}_a+{^S}\mathbf{e}_a
{^S}\mathbf{a}=-{^S}\mathbf{R}_N {^N}\mathbf{g}+{^S}\mathbf{b}_a+{^S}\mathbf{e}_a
{^S}\mathbf{R}_N^\top={^N}\mathbf{R}_S=\mathbf{R}_z(\psi)\mathbf{R}_y(\theta)\mathbf{R}_x(\phi)
IMPORTANTE: este "sensor" tiene una limitante
{^N}\mathbf{g}=\begin{bmatrix} 0 \\ 0 \\ g \end{bmatrix}
{^S}\mathbf{a}=-\begin{bmatrix} -g\sin(\theta) \\ g\cos(\theta)\sin(\phi) \\ g\cos(\phi)\cos(\theta) \end{bmatrix}+{^S}\mathbf{b}_a+{^S}\mathbf{e}_a
{^S}\mathbf{a}=-{^S}\mathbf{R}_N {^N}\mathbf{g}+{^S}\mathbf{b}_a+{^S}\mathbf{e}_a
{^S}\mathbf{R}_N^\top={^N}\mathbf{R}_S=\mathbf{R}_z(\psi)\mathbf{R}_y(\theta)\mathbf{R}_x(\phi)
IMPORTANTE: este "sensor" tiene una limitante
{^N}\mathbf{g}=\begin{bmatrix} 0 \\ 0 \\ g \end{bmatrix}
{^S}\mathbf{a}=-\begin{bmatrix} -g\sin(\theta) \\ g\cos(\theta)\sin(\phi) \\ g\cos(\phi)\cos(\theta) \end{bmatrix}+{^S}\mathbf{b}_a+{^S}\mathbf{e}_a
no aparece el yaw \(\psi\)
{^S}\mathbf{a}=-{^S}\mathbf{R}_N {^N}\mathbf{g}+{^S}\mathbf{b}_a+{^S}\mathbf{e}_a
{^S}\mathbf{R}_N^\top={^N}\mathbf{R}_S=\mathbf{R}_z(\psi)\mathbf{R}_y(\theta)\mathbf{R}_x(\phi)
IMPORTANTE: este "sensor" tiene una limitante
{^N}\mathbf{g}=\begin{bmatrix} 0 \\ 0 \\ g \end{bmatrix}
{^S}\mathbf{a}=-\begin{bmatrix} -g\sin(\theta) \\ g\cos(\theta)\sin(\phi) \\ g\cos(\phi)\cos(\theta) \end{bmatrix}+{^S}\mathbf{b}_a+{^S}\mathbf{e}_a
no aparece el yaw \(\psi\)
por ende, para recuperar la orientación (cuaternión) completa se requiere del apoyo de algún sensor adicional (típicamente un magnetómetro)
{^S}\mathbf{a}=-{^S}\mathbf{R}_N {^N}\mathbf{g}+{^S}\mathbf{b}_a+{^S}\mathbf{e}_a
{^S}\mathbf{R}_N^\top={^N}\mathbf{R}_S=\mathbf{R}_z(\psi)\mathbf{R}_y(\theta)\mathbf{R}_x(\phi)
IMPORTANTE: este "sensor" tiene una limitante
{^N}\mathbf{g}=\begin{bmatrix} 0 \\ 0 \\ g \end{bmatrix}
{^S}\mathbf{a}=-\begin{bmatrix} -g\sin(\theta) \\ g\cos(\theta)\sin(\phi) \\ g\cos(\phi)\cos(\theta) \end{bmatrix}+{^S}\mathbf{b}_a+{^S}\mathbf{e}_a
no aparece el yaw \(\psi\)
por ende, para recuperar la orientación (cuaternión) completa se requiere del apoyo de algún sensor adicional (típicamente un magnetómetro)
*puede obtenerse, sin embargo, un modelo para el acelerómetro que sólo considere los ángulos que puede estimar
\phi=\arctan\left(\dfrac{{^S}a_y}{{^S}a_z}\right)
\theta=\arctan\left(\dfrac{-{^S}a_x}{\sqrt{{^S}a_y^2+{^S}a_z^2}}\right)
\mathbf{y}_k=
\begin{bmatrix} 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 \end{bmatrix}
\mathbf{x}_k + \begin{bmatrix} v_{\phi, k} \\ v_{\theta, k} \end{bmatrix}
v_{\phi,k} \sim \mathcal{N}(0,\sigma^2_\phi)
v_{\theta,k} \sim \mathcal{N}\left(0,\sigma^2_\theta\right)
estas son nuevas varianzas que consideran la incertidumbre de los ángulos como tal
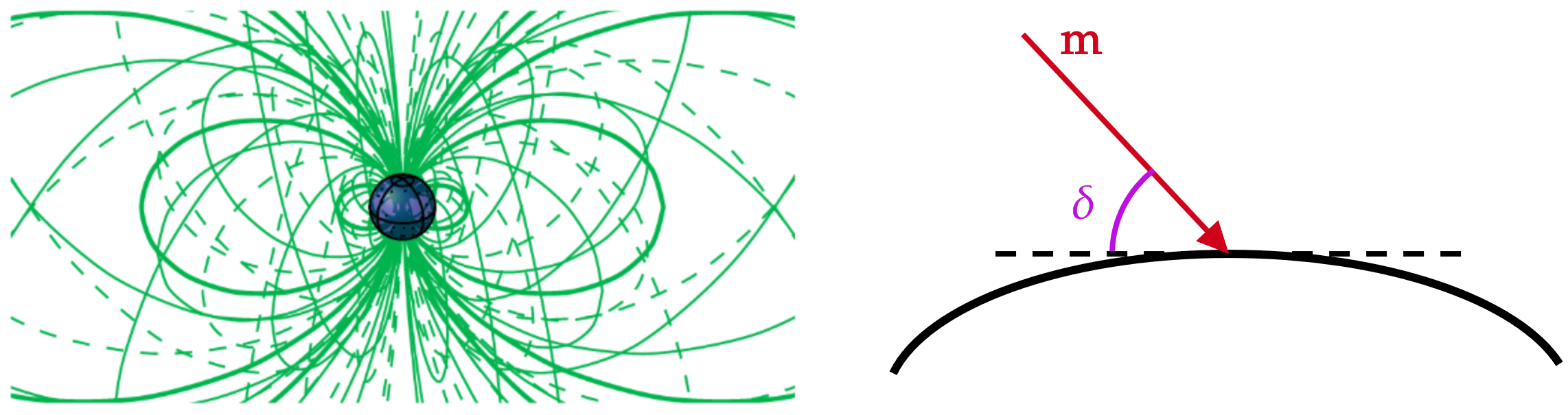
campo magnético de la Tierra
vector de campo magnético en el marco de navegación
Magnetómetros para medir \(\psi\)
si se asume que el sensor no se mueve sobre distancias significativas en comparación al tamaño de la Tierra, el campo magnético local puede asumirse constante
{^N}\mathbf{m}=\begin{bmatrix} \cos\delta \\ 0 \\ \sin\delta \end{bmatrix}=\begin{bmatrix} m_N \\ 0 \\ m_D \end{bmatrix}
si se asume que el sensor no se mueve sobre distancias significativas en comparación al tamaño de la Tierra, el campo magnético local puede asumirse constante
{^N}\mathbf{m}=\begin{bmatrix} \cos\delta \\ 0 \\ \sin\delta \end{bmatrix}=\begin{bmatrix} m_N \\ 0 \\ m_D \end{bmatrix}
inclinación magnética o dip (taza entre las componentes del campo), depende de la posición en la Tierra
{^S}\mathbf{m}={^S}\mathbf{R}_N {^N}\mathbf{m}+{^S}\mathbf{e}_m
\boldsymbol{\mathcal{H}}(\phi_k,\theta_k,\psi_k)
e igualmente el ruido de nuevo toma en consideración la incertidumbre del modelo
{^S}\mathbf{m}={^S}\mathbf{R}_N {^N}\mathbf{m}+{^S}\mathbf{e}_m
\boldsymbol{\mathcal{H}}(\phi_k,\theta_k,\psi_k)
e igualmente el ruido de nuevo toma en consideración la incertidumbre del modelo
este modelo el yaw se considera con respecto al Norte magnético, de necesitar el Norte verdadero debe considerarse también la declinación magnética
\psi_\mathrm{mag}=\arctan\left(\dfrac{{^S}m_y}{{^S}m_x}\right)
\psi_\mathrm{real}=\psi_\mathrm{mag}-\Delta\left({^I}\mathbf{p}\right)
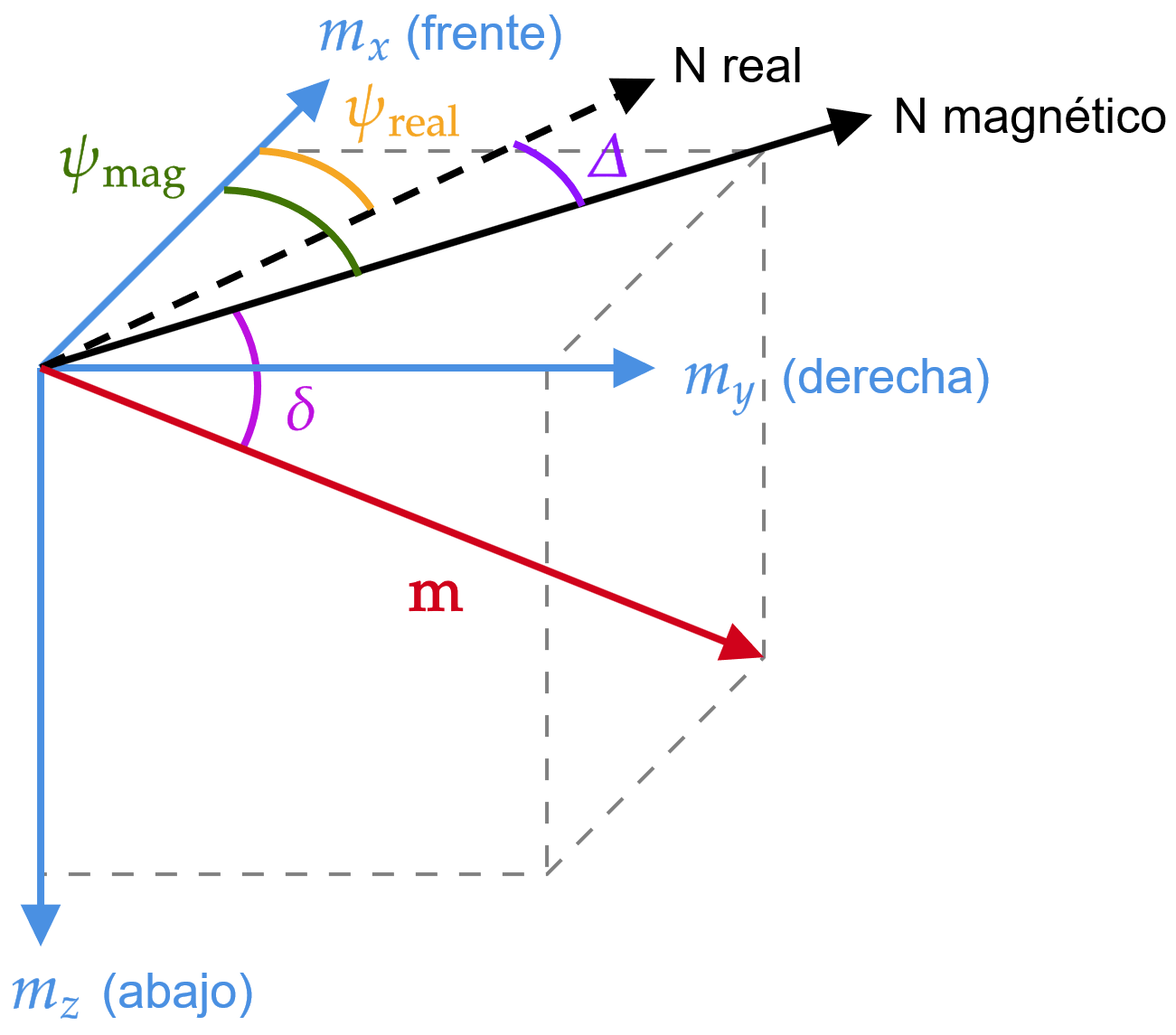
ángulo de declinación magnética (depende de la posición \({^I}\mathbf{p}\) del sensor en el marco de la Tierra)
y_k=\psi_k+v_{\psi,k}
v_{\psi,k} \sim \mathcal{N}\left(0,\sigma^2_\psi\right)
Un último detalle implícito
\{I\}
\{N\}
x \ [\mathrm{North}]
y \ [\mathrm{East}]
z \ [\mathrm{Down}]
Poniéndolo todo junto
IMU + GPS:
Poniéndolo todo junto
IMU + GPS:
Odometría + GPS + brújula:
>> mt3006_clase13_ekfloc.m
Un preámbulo a mapeo:
corrección de pose empleando un mapa conocido
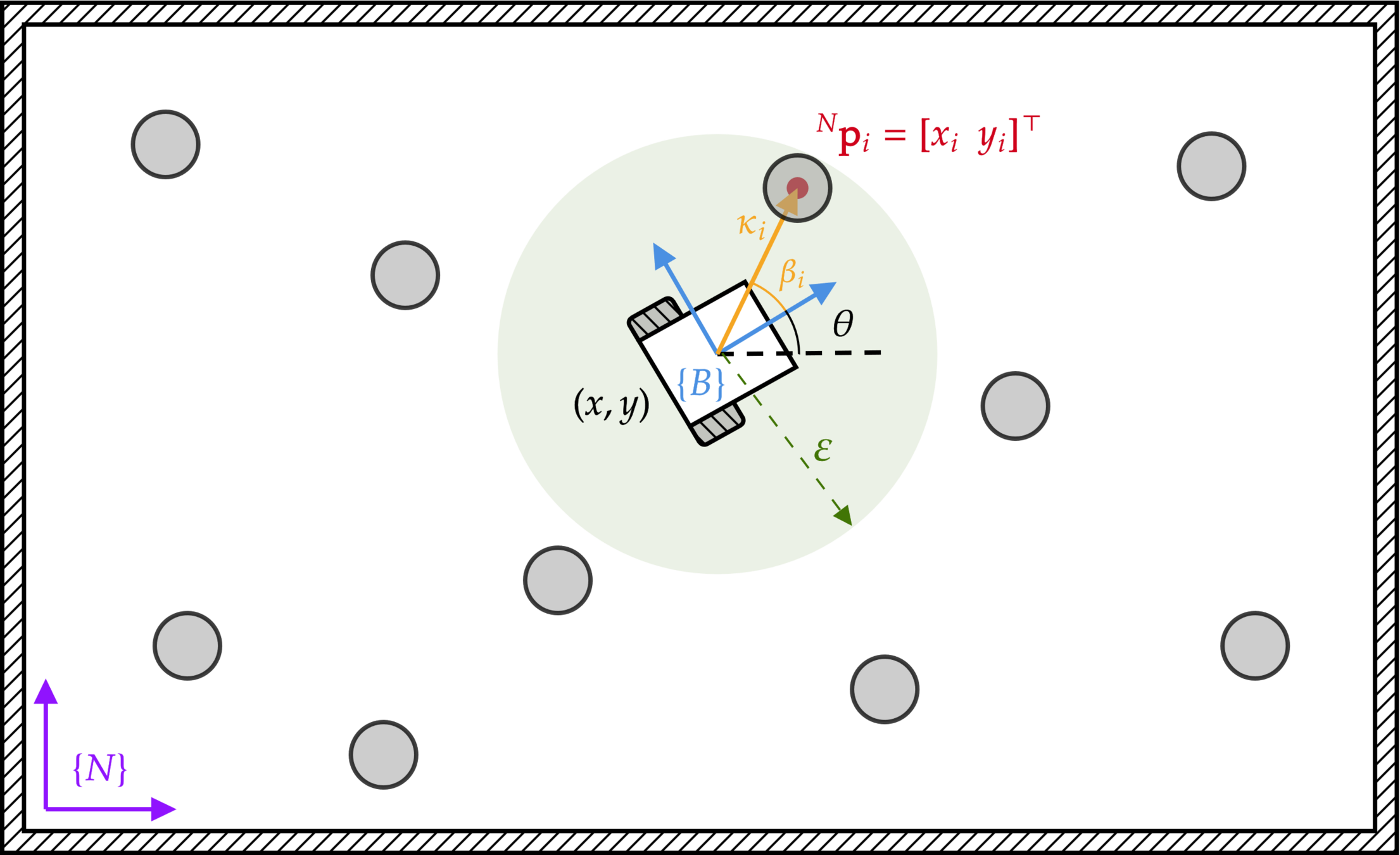
mapa con landmarks conocidos
sensor de posición \(\kappa_i\) + sensor de bearing \(\beta_i\)
"falda" de sensado
landmarks numerados
Referencias
- MT3006 - Localización y mapeo en robótica móvil.pdf
- Kok et. al, Using Inertial Sensors for Position and Orientation Estimation.
- https://ahrs.readthedocs.io/en/latest/filters.html.
MT3006 - Lecture 13 (2024)
By Miguel Enrique Zea Arenales
