SLAM I: mapeo basado en landmarks
MT3006 - Robótica 2
¿SLAM?
Simultaneous Localization And Mapping
Dos casos más simples como preámbulo al problema completo
Caso 1: conocemos el mapa
¿Puede esto ayudar a la localización?
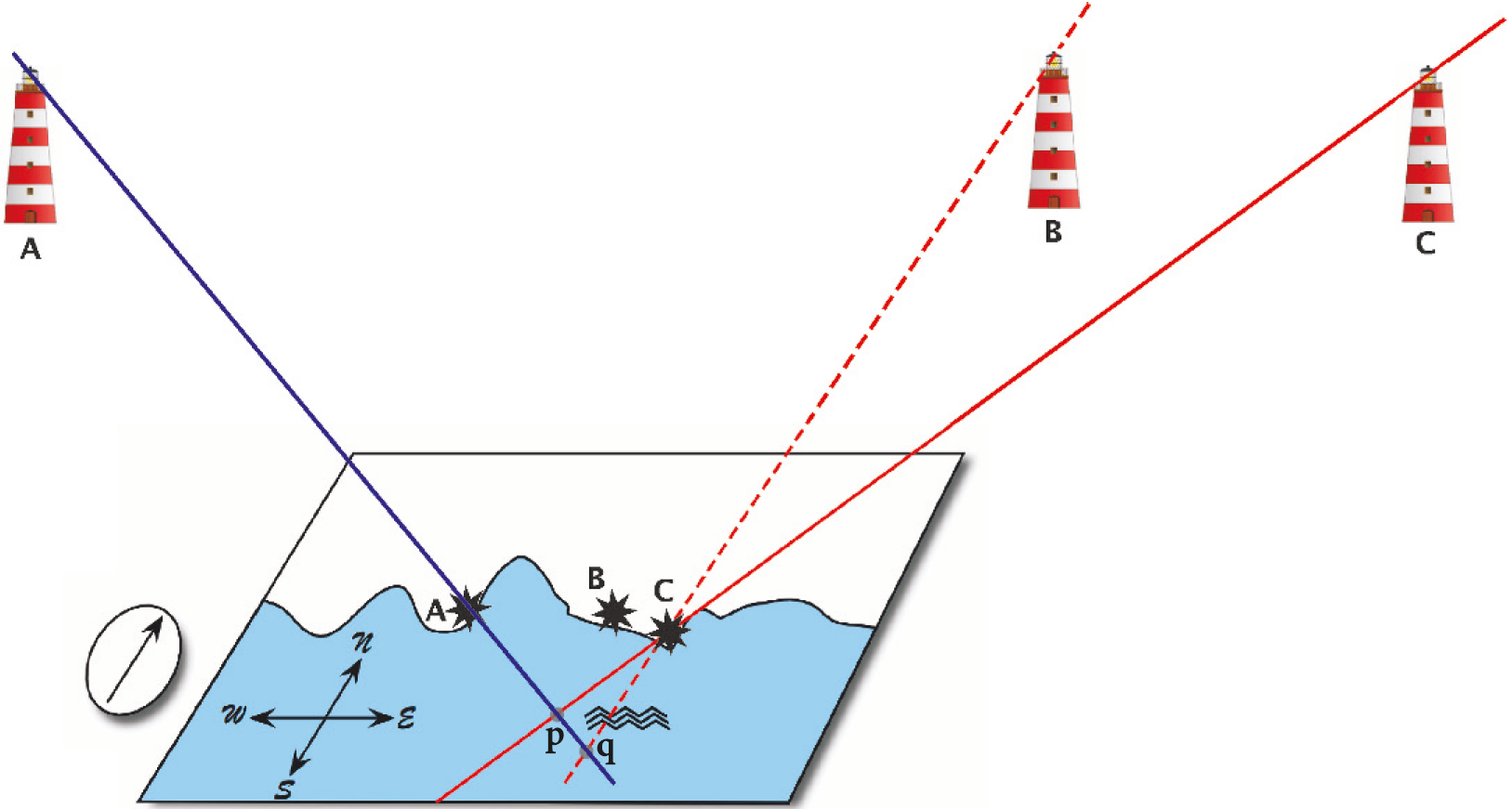
OJO: consideraremos el caso "simple" en donde los "mapas" están definidos por landmarks
1
2
3
4
y_N
x_N
se conoce el mapa
1
2
3
4
y_N
x_N
se conoce el mapa
1
2
3
4
el robot está equipado con sensores de distancia y bearing
y_N
x_N
se conoce el mapa
el robot está equipado con sensores de distancia y bearing
1
2
3
4
se tiene un estimado propioceptivo de la pose que se quiere corregir con el mapa conocido
y_N
x_N
1
2
3
4
\hat{\mathbf{x}}_{1|0}=\text{odometría}\left(\hat{\mathbf{x}}_{0|0}, \mathbf{u}_1\right) \\
\mathbf{P}_{1|0}=\text{odometría}\left(\mathbf{P}_{0|0}\right)
\ t
\mathbf{x}(t)
t_1
t_2
t_3
y
x
\theta
y_N
x_N
1
2
3
4
\hat{\mathbf{x}}_{1|0}=\text{odometría}\left(\hat{\mathbf{x}}_{0|0}, \mathbf{u}_1\right) \\
\mathbf{P}_{1|0}=\text{odometría}\left(\mathbf{P}_{0|0}\right)
\ t
\mathbf{x}(t)
t_1
t_2
t_3
y
x
\theta
NO hay corrección
y_N
x_N
1
2
3
4
continua sólo con odometría pero...
\ t
\mathbf{x}(t)
t_1
t_2
t_3
y
x
\theta
y_N
x_N
1
2
3
4
\ t
\mathbf{x}(t)
t_1
t_2
t_3
y
x
\theta
continua sólo con odometría pero...
(\kappa_1,\beta_1)
...detecta un landmark
y_N
x_N
\mathbf{y}_{1,2}\equiv \mathbf{y}_1(t_2)={^B}\begin{bmatrix} \kappa_1(t_2) \\ \beta_1(t_2) \end{bmatrix}
\mathbf{y}_{1,2}\equiv \mathbf{y}_1(t_2)={^B}\begin{bmatrix} \kappa_1(t_2) \\ \beta_1(t_2) \end{bmatrix}
\mathbf{y}_{1,k}=
\underbrace{\begin{bmatrix} \sqrt{(x_1-\xi_{1,k})^2+(y_1-\xi_{2,k})^2} \\ \arctan\left(\frac{y_1-\xi_{2,k}}{x_1-\xi_{1,k}}\right) -\xi_{3,k} \end{bmatrix}
+\begin{bmatrix} v_\kappa \\ v_\beta \end{bmatrix}}_{{^B}\boldsymbol{\mathcal{G}} \left({^N}\boldsymbol{\xi}_k, {^N}\mathbf{p}_1, \mathbf{v}_k\right)}\\
=\boldsymbol{\mathcal{H}}_1(\mathbf{x}_k)+\mathbf{v}_k
asumiremos que el modelo que genera esta medición es
\mathbf{y}_{1,2}\equiv \mathbf{y}_1(t_2)={^B}\begin{bmatrix} \kappa_1(t_2) \\ \beta_1(t_2) \end{bmatrix}
\mathbf{y}_{1,k}=
\underbrace{\begin{bmatrix} \sqrt{(x_1-\xi_{1,k})^2+(y_1-\xi_{2,k})^2} \\ \arctan\left(\frac{y_1-\xi_{2,k}}{x_1-\xi_{1,k}}\right) -\xi_{3,k} \end{bmatrix}
+\begin{bmatrix} v_\kappa \\ v_\beta \end{bmatrix}}_{{^B}\boldsymbol{\mathcal{G}} \left({^N}\boldsymbol{\xi}_k, {^N}\mathbf{p}_1, \mathbf{v}_k\right)}\\
=\boldsymbol{\mathcal{H}}_1(\mathbf{x}_k)+\mathbf{v}_k
asumiremos que el modelo que genera esta medición es
posición del landmark 1 en el marco de navegación
\mathbf{y}_{1,2}\equiv \mathbf{y}_1(t_2)={^B}\begin{bmatrix} \kappa_1(t_2) \\ \beta_1(t_2) \end{bmatrix}
asumiremos que el modelo que genera esta medición es
\mathbf{C}_{\boldsymbol{\xi}_1}=
\begin{bmatrix} -\frac{x_1-\xi_{1,k}}{\sqrt{(x_1-\xi_{1,k})^2+(y_1-\xi_{2,k})^2}} & -\frac{y_1-\xi_{2,k}}{\sqrt{(x_1-\xi_{1,k})^2+(y_1-\xi_{2,k})^2}} & 0 \\
\frac{y_1-\xi_{2,k}}{(x_1-\xi_{1,k})^2+(y_1-\xi_{2,k})^2} & -\frac{x_1-\xi_{1,k}}{(x_1-\xi_{1,k})^2+(y_1-\xi_{2,k})^2} & -1 \end{bmatrix}
\mathbf{y}_{1,2}\equiv \mathbf{y}_1(t_2)={^B}\begin{bmatrix} \kappa_1(t_2) \\ \beta_1(t_2) \end{bmatrix}
asumiremos que el modelo que genera esta medición es
\mathbf{C}_{\boldsymbol{\xi}_1}=
\begin{bmatrix} -\frac{x_1-\xi_{1,k}}{\sqrt{(x_1-\xi_{1,k})^2+(y_1-\xi_{2,k})^2}} & -\frac{y_1-\xi_{2,k}}{\sqrt{(x_1-\xi_{1,k})^2+(y_1-\xi_{2,k})^2}} & 0 \\
\frac{y_1-\xi_{2,k}}{(x_1-\xi_{1,k})^2+(y_1-\xi_{2,k})^2} & -\frac{x_1-\xi_{1,k}}{(x_1-\xi_{1,k})^2+(y_1-\xi_{2,k})^2} & -1 \end{bmatrix}
existe un modelo idéntico para cada landmark en el mapa
1
2
3
4
\ t
\mathbf{x}(t)
t_1
t_2
t_3
(\kappa_1,\beta_1)
\hat{\mathbf{x}}_{2|1}=\text{odometría}\left(\hat{\mathbf{x}}_{1|1}, \mathbf{u}_2\right) \\
\mathbf{P}_{2|1}=\text{odometría}\left(\mathbf{P}_{1|1}\right)
y
x
\theta
y_N
x_N
1
2
3
4
\ t
\mathbf{x}(t)
t_1
t_2
t_3
(\kappa_1,\beta_1)
\hat{\mathbf{x}}_{2|2}=\hat{\mathbf{x}}_{2|1}+\mathbf{L}_2\left(\boldsymbol{\mathbf{y}_1(t_2)-\mathcal{H}}_1\left(\hat{\mathbf{x}}_{2|1}\right)\right) \\
\mathbf{P}_{2|2}=\mathbf{P}_{2|1}-\mathbf{L}_2\mathbf{C}_{\boldsymbol{\xi}_1}(t_2)\mathbf{P}_{2|1}
y
x
\theta
y_N
x_N
1
2
3
4
\ t
\mathbf{x}(t)
t_1
t_2
t_3
y
x
\theta
(\kappa_1,\beta_1)
(\kappa_2,\beta_2)
\hat{\mathbf{x}}_{3|2}=\text{odometría}\left(\hat{\mathbf{x}}_{2|2}, \mathbf{u}_3\right) \\
\mathbf{P}_{3|2}=\text{odometría}\left(\mathbf{P}_{2|2}\right)
t_3
y_N
x_N
1
2
3
4
\ t
\mathbf{x}(t)
t_1
t_2
t_3
y
x
\theta
(\kappa_1,\beta_1)
(\kappa_2,\beta_2)
\mathbf{z}(t_3)=\begin{bmatrix} \mathbf{y}_1(t_3)-\mathcal{H}_1\left(\hat{\mathbf{x}}_{3|2}\right) \\ \mathbf{y}_2(t_3)-\mathcal{H}_2\left(\hat{\mathbf{x}}_{3|2}\right) \end{bmatrix}
t_3
y_N
x_N
1
2
3
4
\ t
\mathbf{x}(t)
t_1
t_2
t_3
y
x
\theta
(\kappa_1,\beta_1)
(\kappa_2,\beta_2)
\mathbf{C}(t_3)=\begin{bmatrix} \mathbf{C}_{\boldsymbol{\xi}_1}(t_3) \\ \mathbf{C}_{\boldsymbol{\xi}_2}(t_3) \end{bmatrix}
t_3
y_N
x_N
1
2
3
4
\ t
\mathbf{x}(t)
t_1
t_2
t_3
y
x
\theta
(\kappa_1,\beta_1)
(\kappa_2,\beta_2)
\hat{\mathbf{x}}_{3|3}=\hat{\mathbf{x}}_{3|2}+\mathbf{L}_3\mathbf{z}(t_3) \\
\mathbf{P}_{3|3}=\mathbf{P}_{3|2}-\mathbf{L}_3\mathbf{C}(t_3)\mathbf{P}_{3|2}
t_3
y_N
x_N
1
2
3
4
\ t
\mathbf{x}(t)
t_1
t_2
t_3
y
x
\theta
(\kappa_1,\beta_1)
(\kappa_2,\beta_2)
\hat{\mathbf{x}}_{3|3}=\hat{\mathbf{x}}_{3|2}+\mathbf{L}_3\mathbf{z}(t_3) \\
\mathbf{P}_{3|3}=\mathbf{P}_{3|2}-\mathbf{L}_3\mathbf{C}(t_3)\mathbf{P}_{3|2}
t_3
y_N
x_N
el estimado de la pose no volverá a divergir siempre y cuando el robot pueda anclarse a por lo menos un landmark
Caso 2: el robot conoce su pose
¿Puede emplear esto y sus sensores para construir el mapa?
chart of the east coast of New-Holland by James Cook 1770
NO se conoce el mapa
el robot está equipado con sensores de distancia y bearing
pero el robot es capaz de estimar "perfectamente" su pose
y_N
x_N
y_N
x_N
NO se conoce el mapa
el robot está equipado con sensores de distancia y bearing
pero el robot es capaz de estimar "perfectamente" su pose
¿Qué es \(\hat{\mathbf{x}}\) en este caso entonces?
pero el robot es capaz de estimar "perfectamente" su pose
y_N
x_N
NO se conoce el mapa
el robot está equipado con sensores de distancia y bearing
pero el robot es capaz de estimar "perfectamente" su pose
¿Qué es \(\hat{\mathbf{x}}\) en este caso entonces?
los estimados de la posición de los landmarks
dado que iniciamos desconociendo el mapa
\hat{\mathbf{x}}_{0|0}=\begin{bmatrix} \quad \end{bmatrix}
\mathbf{P}_{0|0}=\begin{bmatrix} \quad \end{bmatrix}
M=0
número de landmarks
n=0
dimensión de \(\hat{\mathbf{x}}\)
dado que iniciamos desconociendo el mapa
\hat{\mathbf{x}}_{0|0}=\begin{bmatrix} \quad \end{bmatrix}
\mathbf{P}_{0|0}=\begin{bmatrix} \quad \end{bmatrix}
se irán construyendo conforme se encuentren los landmarks
M=0
número de landmarks
n=0
dimensión de \(\hat{\mathbf{x}}\)
no se ha encontrado ningún landmark
\(\Rightarrow\) el robot sigue explorando
t=t_1
y_N
x_N
se detecta un landmark
t=t_2
?
y_N
x_N
se detecta un landmark
t=t_2
?
(\kappa_?,\beta_?)
y_N
x_N
se detecta un landmark
t=t_2
?
(\kappa_?,\beta_?)
\mathbf{p}_{?}(t_2)= \underbrace{\begin{bmatrix} \xi_1(t_2) + \kappa_?\cos\left(\xi_3(t_2)+\beta_?\right) \\ \xi_2(t_2) + \kappa_?\sin\left(\xi_3(t_2)+\beta_?\right)\end{bmatrix}}_{{^N}\mathbf{g}\left({^N}\boldsymbol{\xi}(t_2),\mathbf{y}_?(t_2)\right)}
\(\Rightarrow\) se emplean los sensores para estimar la posición del landmark
y_N
x_N
¿Es \(\mathbf{p}_?\) un landmark conocido?
¿Es \(\mathbf{p}_?\) un landmark conocido? NO, es un landmark nuevo
\mathbf{p}_?(t_2) \to \mathbf{p}_1(t_2)
(\kappa_?,\beta_?)\to (\kappa_1(t_2),\beta_1(t_2))
¿Es \(\mathbf{p}_?\) un landmark conocido? NO, es un landmark nuevo
\hat{\mathbf{x}}_{2|2}=\begin{bmatrix} \mathbf{p}_1(t_2) \end{bmatrix}
\mathbf{P}_{2|2}=\mathbf{Y}_\mathbf{y}\begin{bmatrix} \mathbf{P}_{1|1} & \mathbf{0}_{n \times 2} \\ \mathbf{0}_{2\times n} & \mathbf{Q}_{vg} \end{bmatrix}\mathbf{Y}_\mathbf{y}^\top
\mathbf{p}_?(t_2) \to \mathbf{p}_1(t_2)
\mathbf{Q}_{vg}=\begin{bmatrix} \sigma_x^2 & 0 \\ 0 & \sigma_y^2 \end{bmatrix}
(\kappa_?,\beta_?)\to (\kappa_1(t_2),\beta_1(t_2))
jacobiano de inserción
varianzas de los componentes de \({^N}\mathbf{g}\)
¿Es \(\mathbf{p}_?\) un landmark conocido? NO, es un landmark nuevo
\mathbf{Y}_\mathbf{y}=\begin{bmatrix} \mathbf{I}_{n \times n} & & \mathbf{0}_{n \times 2} \\ \mathbf{G}_{\boldsymbol{\xi}} & \mathbf{0}_{2\times n-3} & \mathbf{G}_\mathbf{y} \end{bmatrix}
=\begin{bmatrix} \mathbf{I}_{n \times n} & \mathbf{0}_{n \times 2} \\ \mathbf{0}_{2 \times n} & \mathbf{G}_\mathbf{y} \end{bmatrix}
\mathbf{G}_{\boldsymbol{\xi}}=\mathbf{0}_{2 \times 3}
\mathbf{G}_\mathbf{y}=\begin{bmatrix} \cos(\xi_3(t_2) + \beta_1(t_2)) & -\kappa_1(t_2)\sin(\xi_3(t_2)+\beta_1(t_2)) \\
\sin(\xi_3(t_2) + \beta_1(t_2)) & \kappa_1(t_2)\cos(\xi_3(t_2)+\beta_1(t_2))\end{bmatrix}
M=1 \qquad n=2
se detecta un landmark "conocido" y uno nuevo
t=t_3
?
\square
y_N
x_N
se detecta un landmark "conocido" y uno nuevo
t=t_3
?
\square
\mathbf{p}_{?}(t_3)= {^N}\mathbf{g}\left({^N}\boldsymbol{\xi}(t_3),\mathbf{y}_?(t_3)\right)
\mathbf{p}_\square(t_3)= {^N}\mathbf{g}\left({^N}\boldsymbol{\xi}(t_3),\mathbf{y}_\square(t_3)\right)
(\kappa_?,\beta_?)
(\kappa_?,\beta_?)
(\kappa_\square,\beta_\square)
y_N
x_N
tenemos data de un landmark conocido, ¿Pero cómo sabemos cuál es la que corresponde?
\mathbf{p}_?(t_3) \\
\mathbf{p}_\square(t_3)
\mathbf{p}_1(t_3)
tenemos data de un landmark conocido, ¿Pero cómo sabemos cuál es la que corresponde?
\mathbf{p}_?(t_3) \\
\mathbf{p}_\square(t_3)
\mathbf{p}_1(t_3)
PROBLEMA de asignación
tenemos data de un landmark conocido, ¿Pero cómo sabemos cuál es la que corresponde?
\mathbf{p}_?(t_3) \\
\mathbf{p}_\square(t_3)
\mathbf{p}_1(t_3)
PROBLEMA de asignación
- distancia Euclideana (lo que se empleará en el ejemplo, mala pero simple).
- distancia de Mahalanobis.
- features (ej: fiducial markers).
Paréntesis: distancia de Mahalanobis
\mathbf{x}
\mathbf{p}
Paréntesis: distancia de Mahalanobis
\mathbf{x}
\mathbf{p}
\mathbf{d}=\sqrt{\left(\mathbf{x}-\mathbf{p}\right)^\top\left(\mathbf{x}-\mathbf{p}\right)}
Paréntesis: distancia de Mahalanobis
\mathbf{x}
\mathbf{p}
\mathbf{d}=\sqrt{\left(\mathbf{x}-\mathbf{p}\right)^\top\left(\mathbf{x}-\mathbf{p}\right)}
Paréntesis: distancia de Mahalanobis
\mathbf{x}
\mathbf{p}
\mathbf{d}=\sqrt{\left(\mathbf{x}-\mathbf{p}\right)^\top\left(\mathbf{x}-\mathbf{p}\right)}
\mathbf{d}_M=\sqrt{\left(\mathbf{x}-\boldsymbol{\mu}_{\mathbf{p}}\right)^\top \mathbf{Q}_\mathbf{p}^{-1} \left(\mathbf{x}-\boldsymbol{\mu}_{\mathbf{p}}\right)}
generalización del puntaje z
¿A qué tantas desviaciones estándar se encuentra?
Paréntesis: distancia de Mahalanobis
\mathbf{x}
\mathbf{p}
\mathbf{d}=\sqrt{\left(\mathbf{x}-\mathbf{p}\right)^\top\left(\mathbf{x}-\mathbf{p}\right)}
\mathbf{d}_M=\sqrt{\left(\mathbf{x}-\boldsymbol{\mu}_{\mathbf{p}}\right)^\top \mathbf{Q}_\mathbf{p}^{-1} \left(\mathbf{x}-\boldsymbol{\mu}_{\mathbf{p}}\right)}
generalización del puntaje z
¿A qué tantas desviaciones estándar se encuentra?
NOTA: la distancia de Mahalanobis es igual a la distancia Euclideana hacia la media para el caso de varianzas unitarias
entonces, para el landmark conocido
\mathbf{p}_?(t_3) \to \mathbf{p}_1(t_3)
(\kappa_?,\beta_?)\to (\kappa_1(t_3),\beta_1(t_3))
\hat{\mathbf{x}}_{2|2}=\begin{bmatrix} \hat{\mathbf{p}}_{1,2|2} \end{bmatrix}
NOTA: \(\mathbf{p}_?(t_3)\) se emplea sólo para el problema de asignación, dentro del EKF se emplea pero \((\kappa_?,\beta_?)\) ya luego de haberse asignado
entonces, para el landmark conocido
\mathbf{z}(t_3) = \begin{bmatrix} \mathbf{y}_1(t_3)-{^B}\boldsymbol{\mathcal{G}} \left({^N}\boldsymbol{\xi}(t_3), \hat{\mathbf{p}}_{1,3|2}, \mathbf{0}\right)
= \mathbf{y}_1(t_3)-\mathcal{H}_1 \left({^N}\boldsymbol{\xi}(t_3) \right)
\end{bmatrix}
\mathbf{C}(t_3)=\begin{bmatrix} \mathbf{C}_1(t_3) \end{bmatrix}
\mathbf{C}_1(t_3)=
\begin{bmatrix} -\frac{\hat{x}_{1,3|2}-\xi_1(t_3)}{\sqrt{(\hat{x}_{1,3|2}-\xi_1(t_3))^2+(\hat{y}_{1,3|2}-\xi_2(t_3))^2}}
& -\frac{\hat{y}_{1,3|2}-\xi_2(t_3)}{\sqrt{(\hat{x}_{1,3|2}-\xi_1(t_3))^2+(\hat{y}_{1,3|2}-\xi_2(t_3))^2}} \\
\frac{\hat{y}_{1,3|2}-\xi_2(t_3)}{(\hat{x}_{1,3|2}-\xi_1(t_3))^2+(\hat{y}_{1,3|2}-\xi_2(t_3))^2}
& -\frac{\hat{x}_{1,3|2}-\xi_1(t_3)}{(\hat{x}_{1,3|2}-\xi_1(t_3))^2+(\hat{y}_{1,3|2}-\xi_2(t_3))^2} \end{bmatrix}
\hat{\mathbf{p}}_{1,3|2}
entonces, para el landmark conocido
\mathbf{z}(t_3) = \begin{bmatrix} \mathbf{y}_1(t_3)-{^B}\boldsymbol{\mathcal{G}} \left({^N}\boldsymbol{\xi}(t_3), \hat{\mathbf{p}}_{1,3|2}, \mathbf{0}\right)
= \mathbf{y}_1(t_3)-\mathcal{H}_1 \left({^N}\boldsymbol{\xi}(t_3) \right)
\end{bmatrix}
\mathbf{C}(t_3)=\begin{bmatrix} \mathbf{C}_1(t_3) \end{bmatrix}
\mathbf{C}_1(t_3)=
\begin{bmatrix} -\frac{\hat{x}_{1,3|2}-\xi_1(t_3)}{\sqrt{(\hat{x}_{1,3|2}-\xi_1(t_3))^2+(\hat{y}_{1,3|2}-\xi_2(t_3))^2}}
& -\frac{\hat{y}_{1,3|2}-\xi_2(t_3)}{\sqrt{(\hat{x}_{1,3|2}-\xi_1(t_3))^2+(\hat{y}_{1,3|2}-\xi_2(t_3))^2}} \\
\frac{\hat{y}_{1,3|2}-\xi_2(t_3)}{\sqrt{(\hat{x}_{1,3|2}-\xi_1(t_3))^2+(\hat{y}_{1,3|2}-\xi_2(t_3))^2}}
& -\frac{\hat{x}_{1,3|2}-\xi_1(t_3)}{\sqrt{(\hat{x}_{1,3|2}-\xi_1(t_3))^2+(\hat{y}_{1,3|2}-\xi_2(t_3))^2}} \end{bmatrix}
esto corresponde a la predicción, ¿Qué es esto en el problema de mapeo?
(paréntesis)
1
2
3
4
\text{si} \quad \mathbf{x}(t_k)=\begin{bmatrix} \mathbf{p}_1(t_k) \\ \mathbf{p}_2(t_k) \\ \vdots \\ \mathbf{p}_M(t_k) \end{bmatrix}
¿Cuál es la dinámica del mapa?
t=t_0
y_N
x_N
(paréntesis)
1
2
3
4
\text{si} \quad \mathbf{x}(t_k)=\begin{bmatrix} \mathbf{p}_1(t_k) \\ \mathbf{p}_2(t_k) \\ \vdots \\ \mathbf{p}_M(t_k) \end{bmatrix}
¿Cuál es la dinámica del mapa?
t=t_1
y_N
x_N
(paréntesis)
1
2
3
4
\text{si} \quad \mathbf{x}(t_k)=\begin{bmatrix} \mathbf{p}_1(t_k) \\ \mathbf{p}_2(t_k) \\ \vdots \\ \mathbf{p}_M(t_k) \end{bmatrix}
¿Cuál es la dinámica del mapa?
t=t_2
y_N
x_N
(paréntesis)
1
2
3
4
\text{si} \quad \mathbf{x}(t_k)=\begin{bmatrix} \mathbf{p}_1(t_k) \\ \mathbf{p}_2(t_k) \\ \vdots \\ \mathbf{p}_M(t_k) \end{bmatrix}
¿Cuál es la dinámica del mapa?
t=t_{100}
y_N
x_N
(paréntesis)
1
2
3
4
\text{si} \quad \mathbf{x}(t_k)=\begin{bmatrix} \mathbf{p}_1(t_k) \\ \mathbf{p}_2(t_k) \\ \vdots \\ \mathbf{p}_M(t_k) \end{bmatrix}
¿Cuál es la dinámica del mapa?
t=t_{100000}
y_N
x_N
(paréntesis)
1
2
3
4
\text{si} \quad \mathbf{x}(t_k)=\begin{bmatrix} \mathbf{p}_1(t_k) \\ \mathbf{p}_2(t_k) \\ \vdots \\ \mathbf{p}_M(t_k) \end{bmatrix}
¿Cuál es la dinámica del mapa?
t=t_{100000}
y_N
x_N
obviamente el mapa se mantiene estático por lo que
\hat{\mathbf{x}}_{k|k-1}=\hat{\mathbf{x}}_{k-1|k-1} \\
\mathbf{P}_{k|k-1}=\mathbf{P}_{k-1|k-1}
sin ruido de proceso (varianza cero)
(paréntesis)
1
2
3
4
\text{si} \quad \mathbf{x}(t_k)=\begin{bmatrix} \mathbf{p}_1(t_k) \\ \mathbf{p}_2(t_k) \\ \vdots \\ \mathbf{p}_M(t_k) \end{bmatrix}
¿Cuál es la dinámica del mapa?
t=t_{100000}
y_N
x_N
obviamente el mapa se mantiene estático por lo que
\hat{\mathbf{x}}_{k|k-1}=\hat{\mathbf{x}}_{k-1|k-1} \\
\mathbf{P}_{k|k-1}=\mathbf{P}_{k-1|k-1}
sin ruido de proceso (varianza cero)
regresemos al problema...
se detecta un landmark "conocido" y uno nuevo
t=t_3
?
\square
\mathbf{p}_{?}(t_3)= {^N}\mathbf{g}\left({^N}\boldsymbol{\xi}(t_3),\mathbf{y}_?(t_3)\right)
\mathbf{p}_\square(t_3)= {^N}\mathbf{g}\left({^N}\boldsymbol{\xi}(t_3),\mathbf{y}_\square(t_3)\right)
(\kappa_?,\beta_?)
(\kappa_\square,\beta_\square)
y_N
x_N
¿Es \(\mathbf{p}_\square\) un landmark conocido? NO, es un landmark nuevo
\hat{\mathbf{x}}^\mathrm{new}_{3|3}=\begin{bmatrix} \hat{\mathbf{x}}^\mathrm{old}_{3|3} \\ \mathbf{p}_2(t_3) \end{bmatrix}
\mathbf{P}^\mathrm{new}_{3|3}=\mathbf{Y}_\mathbf{y}\begin{bmatrix} \mathbf{P}^\mathrm{old}_{3|3} & \mathbf{0}_{2 \times 2} \\ \mathbf{0}_{2\times 2} & \mathbf{Q}_{vg} \end{bmatrix}\mathbf{Y}_\mathbf{y}^\top
\mathbf{p}_\square(t_3) \to \mathbf{p}_2(t_3)
(\kappa_\square,\beta_\square)\to (\kappa_2(t_3),\beta_2(t_3))
¿Es \(\mathbf{p}_\square\) un landmark conocido? NO, es un landmark nuevo
\mathbf{Y}_\mathbf{y}=\begin{bmatrix} \mathbf{I}_{2 \times 2} & \mathbf{0}_{2 \times 2} \\ \mathbf{0}_{2 \times 2} & \mathbf{G}_\mathbf{y} \end{bmatrix}
\mathbf{G}_\mathbf{y}=\begin{bmatrix} \cos(\xi_3(t_3) + \beta_2(t_3)) & -\kappa_2(t_3)\sin(\xi_3(t_3)+\beta_2(t_3)) \\
\sin(\xi_3(t_3) + \beta_2(t_3)) & \kappa_2(t_3)\cos(\xi_3(t_3)+\beta_2(t_3))\end{bmatrix}
M=2 \qquad n=4
predicción
t=t_4
?
\square
\hat{\mathbf{x}}_{4|3}=\hat{\mathbf{x}}_{3|3} \\
\mathbf{P}_{4|3}=\mathbf{P}_{3|3}
y_N
x_N
predicción
t=t_4
?
\square
\hat{\mathbf{x}}_{4|3}=\hat{\mathbf{x}}_{3|3} \\
\mathbf{P}_{4|3}=\mathbf{P}_{3|3}
(\kappa_?,\beta_?)
(\kappa_\square,\beta_\square)
se detectan dos landmarks "conocidos"
y_N
x_N
predicción
t=t_4
?
\square
\hat{\mathbf{x}}_{4|3}=\hat{\mathbf{x}}_{3|3} \\
\mathbf{P}_{4|3}=\mathbf{P}_{3|3}
(\kappa_?,\beta_?)
(\kappa_\square,\beta_\square)
\mathbf{p}_{?}(t_4)= {^N}\mathbf{g}\left({^N}\boldsymbol{\xi}(t_4),\mathbf{y}_?(t_4)\right)
\mathbf{p}_\square(t_4)= {^N}\mathbf{g}\left({^N}\boldsymbol{\xi}(t_4),\mathbf{y}_\square(t_4)\right)
y_N
x_N
para los landmarks conocidos
\mathbf{p}_?(t_4) \to \mathbf{p}_1(t_4)
(\kappa_?,\beta_?)\to (\kappa_1(t_4),\beta_1(t_4))
\mathbf{p}_\square(t_4) \to \mathbf{p}_2(t_4)
(\kappa_\square,\beta_\square)\to (\kappa_2(t_4),\beta_2(t_4))
\mathbf{z}(t_4) = \begin{bmatrix} \mathbf{y}_1(t_4)-\mathcal{H}_1 \left({^N}\boldsymbol{\xi}(t_4) \right) \\ \mathbf{y}_2(t_4)-\mathcal{H}_2 \left({^N}\boldsymbol{\xi}(t_4) \right)
\end{bmatrix}
\mathbf{C}(t_4)=\begin{bmatrix} \mathbf{C}_1(t_4) & \mathbf{0}_{2 \times 2} \\ \mathbf{0}_{2 \times 2} & \mathbf{C}_2(t_4) \end{bmatrix}
NOTA: por el cambio en \(\mathbf{C}\), el cálculo de la ganancia de Kalman debe ser
\mathbf{L}_k=\mathbf{P}_{k|k-1}\mathbf{C}^\top\left(\mathbf{C}\mathbf{P}_{k|k-1}\mathbf{C}^\top+\mathbf{I}_{M \times M} \otimes \mathbf{Q}_{v\mathcal{G}}\right)^{-1}
\mathbf{Q}_{v\mathcal{G}}=\begin{bmatrix} \sigma_\kappa^2 & 0 \\ 0 & \sigma_\beta^2 \end{bmatrix}
covarianzas para las mediciones de los sensores de posición y bearing
producto de Kronecker
predicción
t=t_5
?
\square
\hat{\mathbf{x}}_{5|4}=\hat{\mathbf{x}}_{4|4} \\
\mathbf{P}_{5|4}=\mathbf{P}_{4|4}
y_N
x_N
predicción
t=t_5
?
\square
\hat{\mathbf{x}}_{5|4}=\hat{\mathbf{x}}_{4|4} \\
\mathbf{P}_{5|4}=\mathbf{P}_{4|4}
(\kappa_?,\beta_?)
se detecta un landmark "conocido" pero ya no puede verse al otro
y_N
x_N
landmark conocido
\mathbf{p}_?(t_5) \to \mathbf{p}_1(t_5)
(\kappa_?,\beta_?)\to (\kappa_1(t_5),\beta_1(t_5))
\mathbf{p}_2(t_5)=\begin{bmatrix} \quad \end{bmatrix}
(\kappa_2(t_5),\beta_2(t_5))=(\quad , \quad )
\mathbf{z}(t_5) = \begin{bmatrix} \mathbf{y}_1(t_5)-\mathcal{H}_1 \left({^N}\boldsymbol{\xi}(t_5) \right) \\ \mathbf{0}_{2 \times 1} \end{bmatrix}
\mathbf{C}(t_5)=\begin{bmatrix} \mathbf{C}_1(t_5) & \mathbf{0}_{2 \times 2} \\ \mathbf{0}_{2 \times 2} & \mathbf{0} \end{bmatrix}
landmark fuera de rango
\mathbf{C}_2(t_5)
NOTA: lo anterior asume que se hace la corrección en un solo paso, pero también se puede hacer por landmark
\boldsymbol{\ell}_5= \mathbf{P}_{5|4}^{(1)}\mathbf{C}_1^\top(t_5)\left(\mathbf{C}_1(t_5)\mathbf{P}_{5|4}^{(1)}\mathbf{C}_1^\top(t_5)+\mathbf{Q}_{v\mathcal{G}}\right)^{-1}\\
\hat{\mathbf{p}}_{1,5|5}=
\hat{\mathbf{p}}_{1,5|4}+\boldsymbol{\ell}_5\left(\mathbf{y}_1(t_5)-\mathcal{H}_1 \left({^N}\boldsymbol{\xi}(t_5) \right) \right) \\
\mathbf{P}_{5|5}^{(1)}=\mathbf{P}_{5|4}^{(1)}-\boldsymbol{\ell}_5\mathbf{C}_1(t_5)\mathbf{P}_{5|4}^{(1)}
\mathbf{P}_{5|4}^{(1)}=\mathbf{P}_{5|4}(1:2, 1:2)
\mathbf{P}_{5|5}(1:2, 1:2)=\mathbf{P}_{5|5}^{(1)}
NOTA: lo anterior asume que se hace la corrección en un solo paso, pero también se puede hacer por landmark
\boldsymbol{\ell}_5= \mathbf{P}_{5|4}^{(1)}\mathbf{C}_1^\top(t_5)\left(\mathbf{C}_1(t_5)\mathbf{P}_{5|4}^{(1)}\mathbf{C}_1^\top(t_5)+\mathbf{Q}_{v\mathcal{G}}\right)^{-1}\\
\hat{\mathbf{p}}_{1,5|5}=
\hat{\mathbf{p}}_{1,5|4}+\boldsymbol{\ell}_5\left(\mathbf{y}_1(t_5)-\mathcal{H}_1 \left({^N}\boldsymbol{\xi}(t_5) \right) \right) \\
\mathbf{P}_{5|5}^{(1)}=\mathbf{P}_{5|4}^{(1)}-\boldsymbol{\ell}_5\mathbf{C}_1(t_5)\mathbf{P}_{5|4}^{(1)}
\mathbf{P}_{5|4}^{(1)}=\mathbf{P}_{5|4}(1:2, 1:2)
\mathbf{P}_{5|5}(1:2, 1:2)=\mathbf{P}_{5|5}^{(1)}
esto sólo es posible hacerlo en el caso de mapeo (con el EKF), por la estructura diagonal por bloques que presenta la matriz de covarianza
implica que la estimación de cada landmark es independiente con respecto del resto
\mathbf{P}=\begin{bmatrix}
\boldsymbol\square & \mathbf{0} & \mathbf{0} & \cdots & \mathbf{0} \\
\mathbf{0} & \boldsymbol\square & \mathbf{0} & \cdots & \mathbf{0} \\
\mathbf{0} & \mathbf{0} & \boldsymbol\square & \cdots & \mathbf{0} \\
\vdots & \vdots & \vdots & \ddots & \vdots \\
\mathbf{0} & \mathbf{0} & \mathbf{0} & \cdots & \boldsymbol\square
\end{bmatrix}
Poniéndolo todo junto
>> mt3006_clase14_ekfmapping.m
Referencias
- MT3006 - Localización y mapeo en robótica móvil.pdf
- P. Corke, Robotics Vision and Control Fundamentals 2nd Ed., capítulo 6.
MT3006 - Lecture 14 (2024)
By Miguel Enrique Zea Arenales
