MT3006 - Robótica 2
Técnicas clásicas de visión por computadora II
¿Por qué?
Recuperando información 3D a partir de imágenes 2D
¿Cuándo puede revertirse el mapeo?
¿Cuándo puede revertirse el mapeo?
3 posibles casos
¿Cuándo puede revertirse el mapeo?
\tilde{\mathbf{s}}=\mathbf{C}{^I}\tilde{\mathbf{p}}
¿Cuándo puede revertirse el mapeo?
\tilde{\mathbf{s}}=\mathbf{C}{^I}\tilde{\mathbf{p}}
conocida \(3 \times 4\)
conocido \(3 \times 1\)
desconocido \(4 \times 1\)
¿Cuándo puede revertirse el mapeo?
\tilde{\mathbf{s}}=\mathbf{C}{^I}\tilde{\mathbf{p}}
conocida \(3 \times 4\)
conocido \(3 \times 1\)
desconocido \(4 \times 1\)
Es decir, ¿De pixeles a puntos? (caso 1)
¿Cuándo puede revertirse el mapeo?
\tilde{\mathbf{s}}=\mathbf{C}{^I}\tilde{\mathbf{p}}
conocida \(3 \times 4\)
conocido \(3 \times 1\)
desconocido \(4 \times 1\)
\(\mathbf{C}\) no es cuadrada, el mapeo no es único (consecuencia de la proyección)
¿Cuándo puede revertirse el mapeo?
\tilde{\mathbf{s}}=\mathbf{C}{^I}\tilde{\mathbf{p}}
conocida \(3 \times 4\)
conocido \(3 \times 1\)
desconocido \(4 \times 1\)
\(\mathbf{C}\) no es cuadrada, el mapeo no es único (proyección)
Si no se pueden emplear (directamente) los puntos transformados, ¿Qué se puede usar?
¿Cuándo puede revertirse el mapeo?
\tilde{\mathbf{s}}=\mathbf{C}{^I}\tilde{\mathbf{p}}
la transformación como tal
¿Cuándo puede revertirse el mapeo?
\tilde{\mathbf{s}}=\mathbf{C}{^I}\tilde{\mathbf{p}}
desconocida \(3 \times 4=12\) parámetros (11 GDL)
\(=\)\(\mathbf{K}\) \({^C}\mathbf{T}_I\)
¿Cuándo puede revertirse el mapeo?
\tilde{\mathbf{s}}=\mathbf{C}{^I}\tilde{\mathbf{p}}
desconocida \(3 \times 4=12\) parámetros (11 GDL)
\(=\)\(\mathbf{K}\) \({^C}\mathbf{T}_I\)
si no se conoce nada sobre la cámara, los parámetros son una mezcla de los intrínsecos con los extrínsecos
¿Cuándo puede revertirse el mapeo?
\tilde{\mathbf{s}}=\mathbf{C}{^I}\tilde{\mathbf{p}}
\(n\) conocidos \(3 \times 1\)
\(n\) conocidos \(4 \times 1\)
desconocida \(3 \times 4=12\) parámetros (11 GDL)
\(=\)\(\mathbf{K}\) \({^C}\mathbf{T}_I\)
Idea: usar correspondencias entre puntos para plantear un sistema de ecuaciones y estimar los parámetros
¿Cuándo puede revertirse el mapeo?
\tilde{\mathbf{s}}=\mathbf{C}{^I}\tilde{\mathbf{p}}
\(n\) conocidos \(3 \times 1\)
\(n\) conocidos \(4 \times 1\)
desconocida \(3 \times 4=12\) parámetros (11 GDL)
\(=\)\(\mathbf{K}\) \({^C}\mathbf{T}_I\)
encontrar intrínsecos* + extrínsecos
\(\Rightarrow\) calibración de cámara (caso 2)
¿Cuándo puede revertirse el mapeo?
\tilde{\mathbf{s}}=\mathbf{C}{^I}\tilde{\mathbf{p}}
\(n\) conocidos \(3 \times 1\)
\(n\) conocidos \(4 \times 1\)
desconocida \(3 \times 4=12\) parámetros (11 GDL)
\(=\)\(\mathbf{K}\) \({^C}\mathbf{T}_I\)
*la distorsión de la lente suele encontrarse por separado
¿Cuándo puede revertirse el mapeo?
\tilde{\mathbf{s}}=\mathbf{C}{^I}\tilde{\mathbf{p}}
\(n\) conocidos \(3 \times 1\)
\(n\) conocidos \(4 \times 1\)
desconocida \(3 \times 4=12\) parámetros (11 GDL)
\(=\)\(\mathbf{K}\) \({^C}\mathbf{T}_I\)
*la distorsión de la lente suele encontrarse por separado
En general, puede hacerse resolviendo el problema de Perspective\(-n-\)Point (P\(n\)P)
Problema P\(n\)P
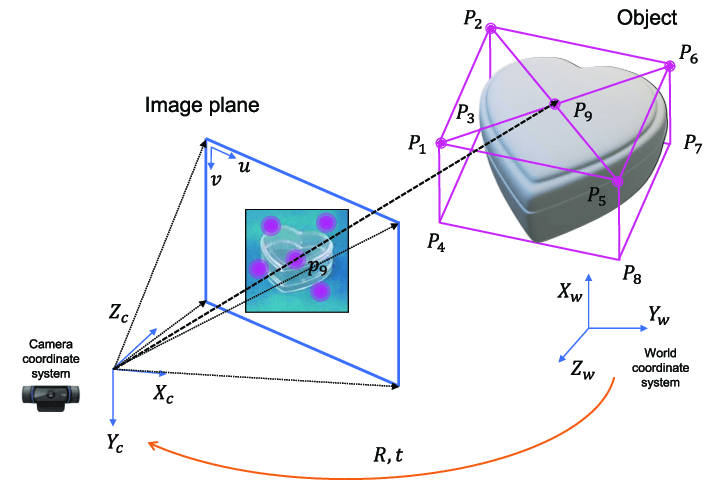
Se emplean \(n\) correspondencias entre puntos 3D y sus respectivas proyecciones en 2D para estimar los parámetros del mapeo
Problema P\(n\)P
- P3P: cuatro soluciones para puntos no colineales.
- P4P y P5P: dos soluciones para puntos no coplanares, única solución para cuatro puntos coplanares (no colineales).
- P\(n\)P: con \(n\ge 6\) puntos no coplanares tiene una única solución.
Problema P\(n\)P
- P3P: cuatro soluciones para puntos no colineales.
- P4P y P5P: dos soluciones para puntos no coplanares, única solución para cuatro puntos coplanares (no colineales).
- P\(n\)P: con \(n\ge 6\) puntos no coplanares tiene una única solución.
Mediante el algoritmo Direct Linear Transform (DLT)
(se transforma el mapeo de proyección a un sistema lineal homogéneo para resolver con métodos estándar)
Problema P\(n\)P
- P3P: cuatro soluciones para puntos no colineales.
- P4P y P5P: dos soluciones para puntos no coplanares, única solución para cuatro puntos coplanares (no colineales).
- P\(n\)P: con \(n\ge 6\) puntos no coplanares tiene una única solución.
método de calibración de Tsai
método de calibración de Zhang
Mediante el algoritmo Direct Linear Transform (DLT)
(se transforma el mapeo de proyección a un sistema lineal homogéneo para resolver con métodos estándar)
puntos no coplanares
puntos coplanares
Problema P\(n\)P
- P3P: cuatro soluciones para puntos no colineales.
- P4P y P5P: dos soluciones para puntos no coplanares, única solución para cuatro puntos coplanares (no colineales).
- P\(n\)P: con \(n\ge 6\) puntos no coplanares tiene una única solución.
método de calibración de Tsai
método de calibración de Zhang
Mediante el algoritmo Direct Linear Transform (DLT)
(se transforma el mapeo de proyección a un sistema lineal homogéneo para resolver con métodos estándar)
puntos no coplanares
puntos coplanares
OpenCV emplea el mismo método de calibración
\dfrac{1}{\tilde{w}}\begin{bmatrix} u \\ v \\ 1 \end{bmatrix}=
\begin{bmatrix} f/\rho_w & 0 & u_0 & 0 \\ 0 & f/\rho_h & v_0 & 0 \\ 0 & 0 & 1 & 0 \end{bmatrix}
\begin{bmatrix} r_{11} & r_{12} & r_{13} & o_x \\ r_{21} & r_{22} & r_{23} & o_y \\ r_{31} & r_{32} & r_{33} & o_z \\ 0 & 0 & 0 & 1 \end{bmatrix}
\begin{bmatrix} x \\ y \\ z \\ 1 \end{bmatrix}
¿Por qué?
\dfrac{1}{\tilde{w}}\begin{bmatrix} u \\ v \\ 1 \end{bmatrix}=
\begin{bmatrix} f/\rho_w & 0 & u_0 & 0 \\ 0 & f/\rho_h & v_0 & 0 \\ 0 & 0 & 1 & 0 \end{bmatrix}
\begin{bmatrix} r_{11} & r_{12} & r_{13} & o_x \\ r_{21} & r_{22} & r_{23} & o_y \\ r_{31} & r_{32} & r_{33} & o_z \\ 0 & 0 & 0 & 1 \end{bmatrix}
\begin{bmatrix} x \\ y \\ z \\ 1 \end{bmatrix}
¿Por qué?
mismo \(z\) para puntos coplanares, \(z=0\) por conveniencia
¿Por qué?
\dfrac{1}{\tilde{w}}\begin{bmatrix} u \\ v \\ 1 \end{bmatrix}=
\begin{bmatrix} h_{11} & h_{12} & h_{13} \\ h_{21} & h_{22} & h_{23} \\ h_{31} & h_{32} & h_{33} \end{bmatrix}
\begin{bmatrix} x \\ y \\ 1 \end{bmatrix}
\dfrac{1}{\tilde{w}}\begin{bmatrix} u \\ v \\ 1 \end{bmatrix}=
\begin{bmatrix} f/\rho_w & 0 & u_0 & 0 \\ 0 & f/\rho_h & v_0 & 0 \\ 0 & 0 & 1 & 0 \end{bmatrix}
\begin{bmatrix} r_{11} & r_{12} & r_{13} & o_x \\ r_{21} & r_{22} & r_{23} & o_y \\ r_{31} & r_{32} & r_{33} & o_z \\ 0 & 0 & 0 & 1 \end{bmatrix}
\begin{bmatrix} x \\ y \\ z \\ 1 \end{bmatrix}
¿Por qué?
\dfrac{1}{\tilde{w}}\begin{bmatrix} u \\ v \\ 1 \end{bmatrix}=
\begin{bmatrix} h_{11} & h_{12} & h_{13} \\ h_{21} & h_{22} & h_{23} \\ h_{31} & h_{32} & h_{33} \end{bmatrix}
\begin{bmatrix} x \\ y \\ 1 \end{bmatrix}
\(\mathbf{H}\equiv\) homografía
\dfrac{1}{\tilde{w}}\begin{bmatrix} u \\ v \\ 1 \end{bmatrix}=
\begin{bmatrix} f/\rho_w & 0 & u_0 & 0 \\ 0 & f/\rho_h & v_0 & 0 \\ 0 & 0 & 1 & 0 \end{bmatrix}
\begin{bmatrix} r_{11} & r_{12} & r_{13} & o_x \\ r_{21} & r_{22} & r_{23} & o_y \\ r_{31} & r_{32} & r_{33} & o_z \\ 0 & 0 & 0 & 1 \end{bmatrix}
\begin{bmatrix} x \\ y \\ z \\ 1 \end{bmatrix}
Tipos de transformaciones en 2D
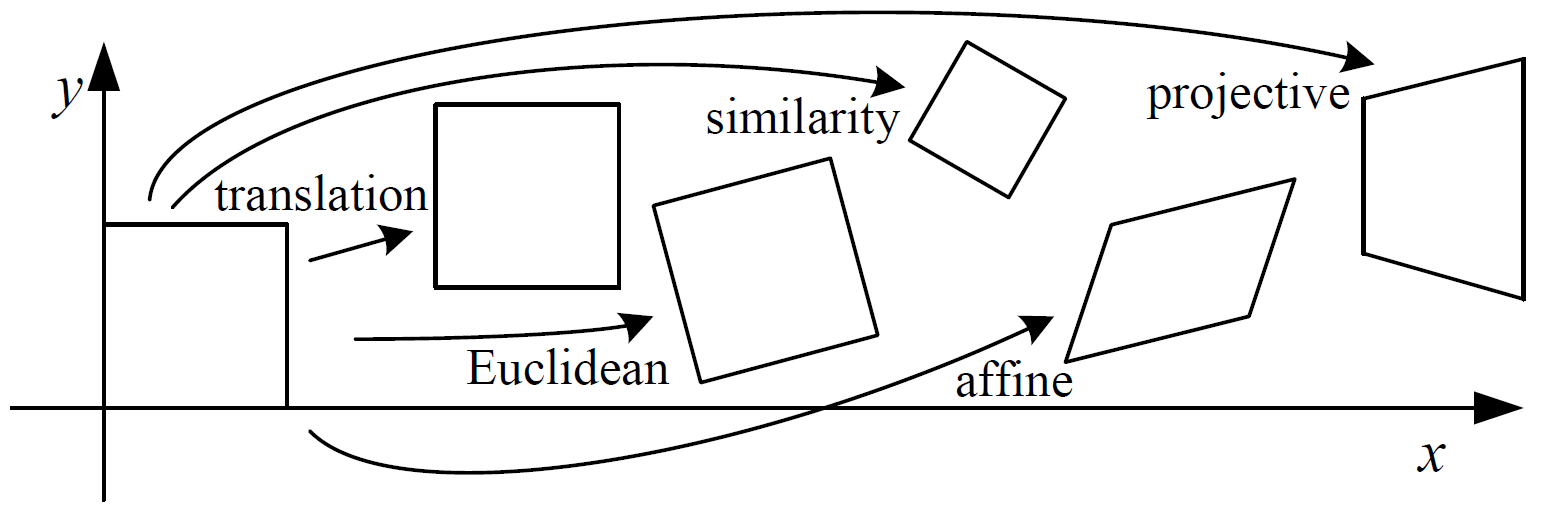
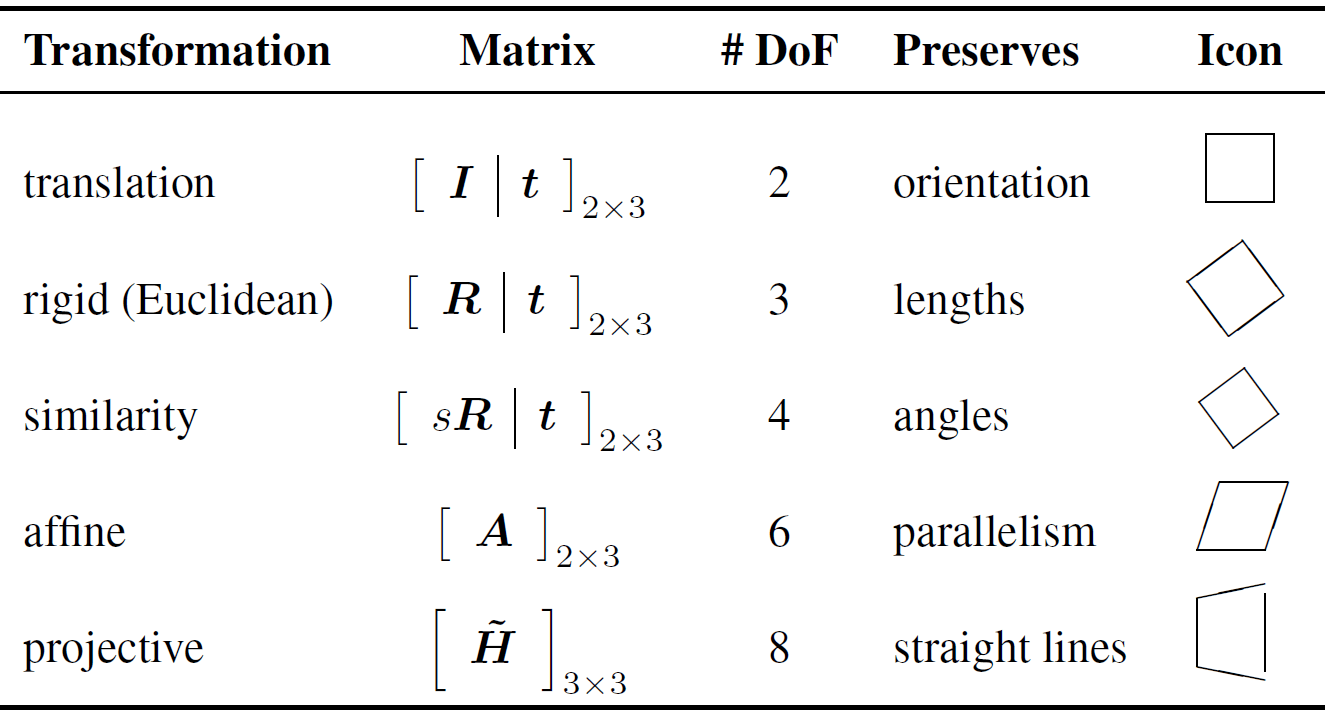
Tipos de transformaciones en 2D
\mathbf{H}
>> mt3006_clase3_homografia.m
Ejemplo: tags y (fiducial) markers
>> mt3006_clase3_apriltags1.m
>> mt3006_clase3_apriltags2.m
Ejemplo: realidad aumentada
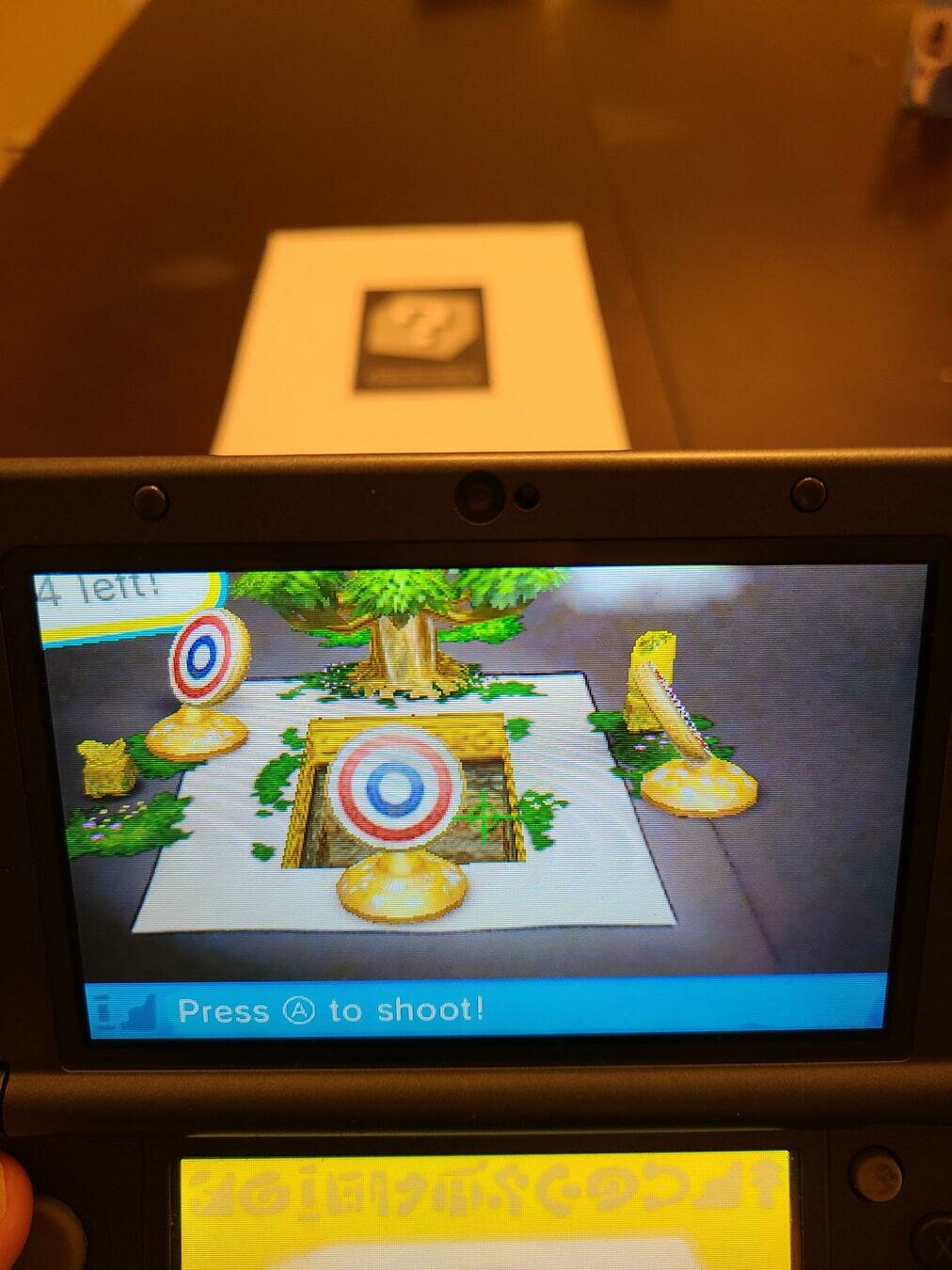
Ejemplo: realidad aumentada
Regresando al último caso
¿Cuándo puede revertirse el mapeo?
\tilde{\mathbf{s}}=\mathbf{C}{^I}\tilde{\mathbf{p}}
desconocida \(4 \times 4=16\) parámetros (6 GDL)
\(=\)\(\mathbf{K}\) \({^C}\mathbf{T}_I\)
se conocen los intrínsecos (cámara calibrada), entonces los parámetros corresponden a los extrínsecos (pose de la cámara)
¿Cuándo puede revertirse el mapeo?
\tilde{\mathbf{s}}=\mathbf{C}{^I}\tilde{\mathbf{p}}
desconocida \(4 \times 4=16\) parámetros (6 GDL)
\(=\)\(\mathbf{K}\) \({^C}\mathbf{T}_I\)
\(n\) conocidos \(3 \times 1\)
\(n\) conocidos \(4 \times 1\)
Idea: misma que antes, usar correspondencias entre puntos para estimar los parámetros (P\(n\)P)
¿Cuándo puede revertirse el mapeo?
\tilde{\mathbf{s}}=\mathbf{C}{^I}\tilde{\mathbf{p}}
desconocida \(4 \times 4=16\) parámetros (6 GDL)
\(=\)\(\mathbf{K}\) \({^C}\mathbf{T}_I\)
\(n\) conocidos \(3 \times 1\)
\(n\) conocidos \(4 \times 1\)
intrínsecos conocidos, encontrar extrínsecos
\(\Rightarrow\) localización de cámara (caso 3)
Localización de cámara
- Si bien puede emplearse de nuevo DLT para resolver este problema, es subóptimo.
- Algunas alternativas de algoritmos son:
- P3P: SOLVEPNP_P3P (OpenCV), estworldpose (MATLAB), SOLVEPNP_AP3P (OpenCV).
- P\(n\)P con \(n\ge 4\): SOLVEPNP_EPNP (OpenCV, Efficient PnP). El EPnP es hasta 10 veces más robusto, exacto y eficiente que el DLT.
Ejemplo: headsets de realidad virtual
Ejemplo: odometría visual
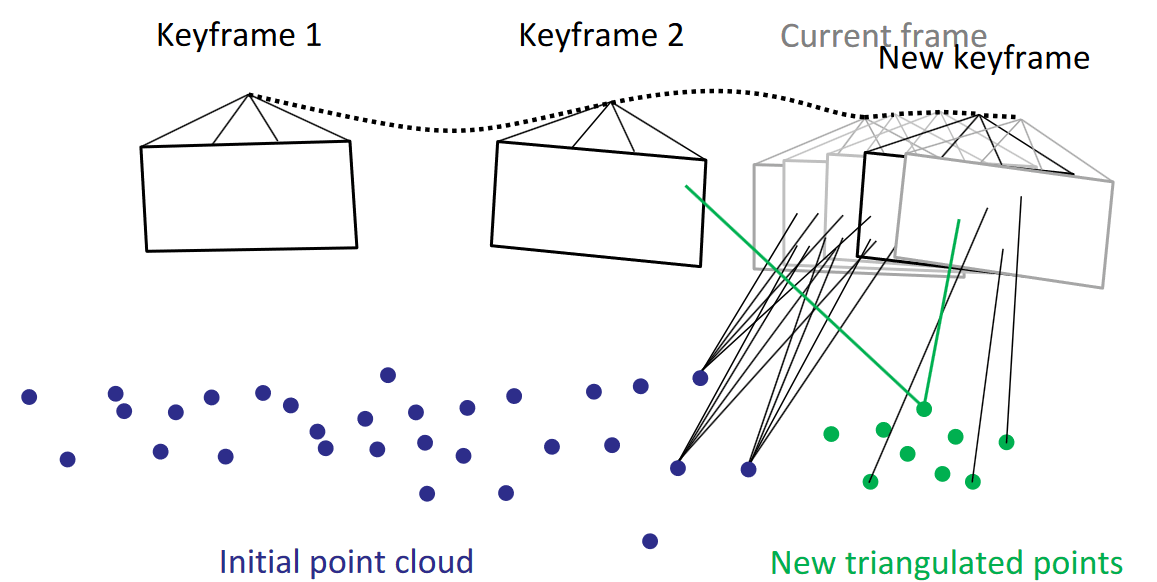
Ejemplo: odometría visual
Limitantes
Por la naturaleza de las imágenes, puede que haya una cantidad considerable de puntos atípicos, dificultando las correspondencias 3D-2D.
Por lo tanto, suelen combinarse los algoritmos de P\(n\)P con el algoritmo RANSAC para obviar los puntos atípicos.
1.
Random Sample Consensus (RANSAC)
Algoritmo iterativo para la estimación paramétrica en la presencia de puntos atípicos.
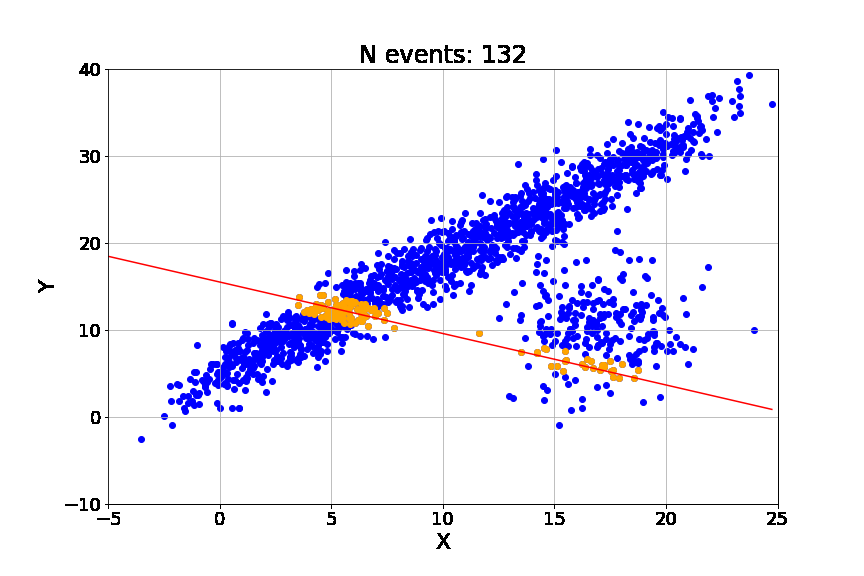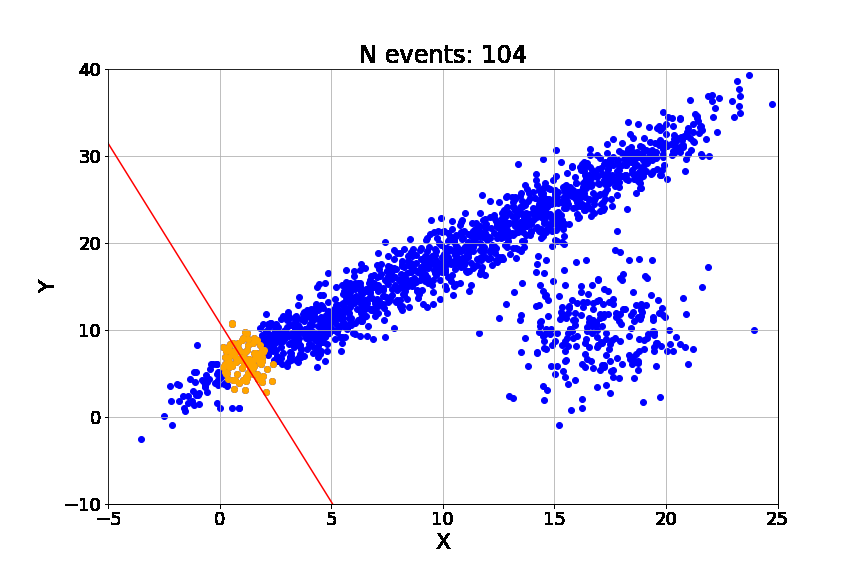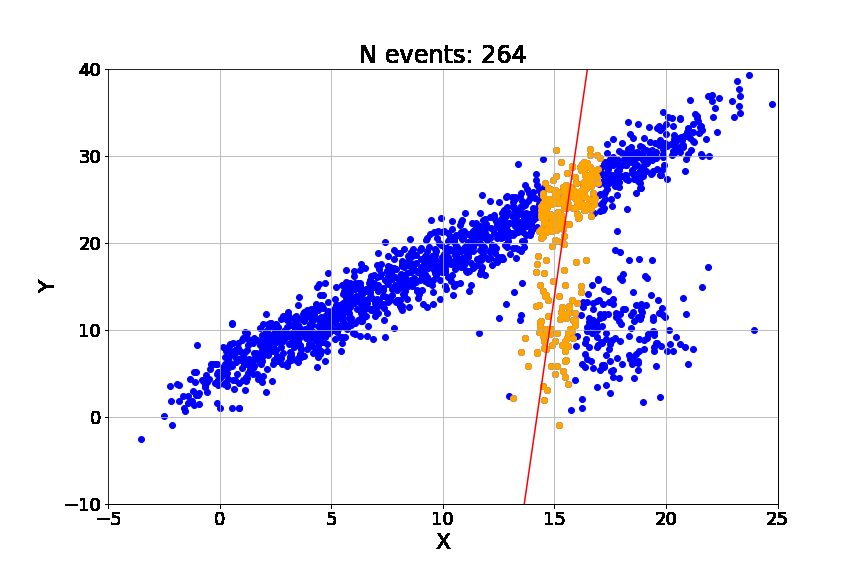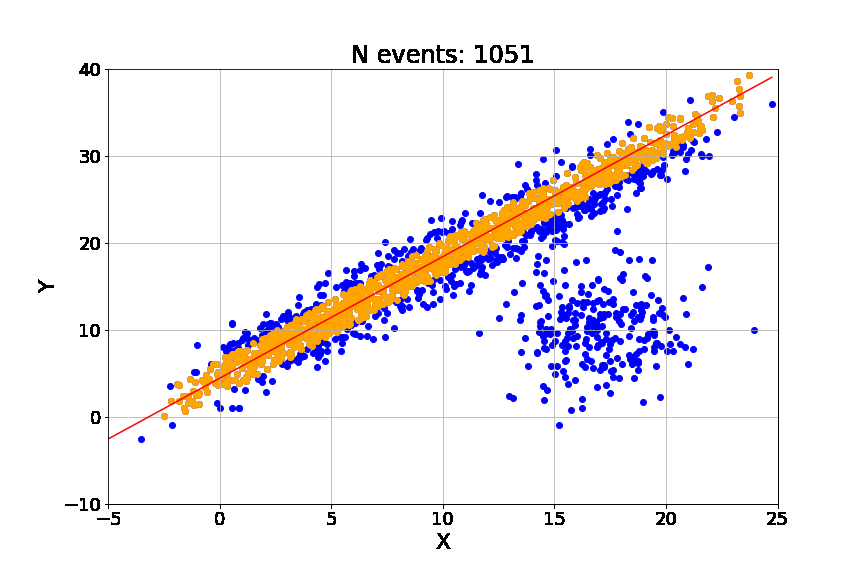
Limitantes
¿Qué ocurre cuándo se tienen sólo imágenes, sin información 3D como para hacer correspondencias?
Pueden seguir utilizándose las correspondencias entre puntos pero ahora usando múltiples imágenes (de la misma situación), mediante características (features).
2.
Detección y correspondencia de características
(feature detection and matching)
Idea general: template matching
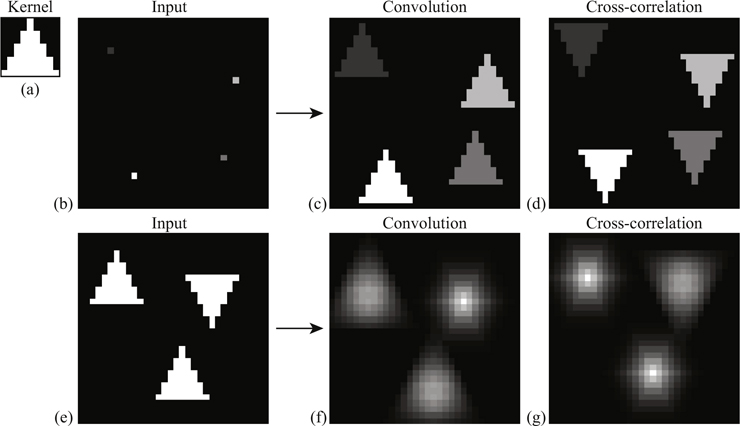
Idea general: template matching pero evitando sus problemas
Idea general: template matching pero evitando sus problemas
- Cambios geométricos: rotación, escala, perspectiva
- Cambios de iluminación.
- Cambios de apariencia.
Idea general: template matching pero evitando sus problemas
- Cambios geométricos: rotación, escala, perspectiva
- Cambios de iluminación.
- Cambios de apariencia.
¿Una mejor opción?
Ejemplo: alineando dos imágenes
Ejemplo: alineando dos imágenes
Ejemplo: alineando dos imágenes
keypoints
...
...
Ejemplo: alineando dos imágenes
keypoints
...
...
¿Cómo seleccionarlos?
Consideración 1: deben detectarse los mismos puntos de forma independiente en ambas imágenes
no puede hacerse la correspondencia si no son los mismos puntos
\(\Rightarrow\) se requiere un detector de features repetible
Consideración 2: debe poderse hacer la correspondencia del mismo punto en ambas imágenes
¿Cuál corresponde a cuál?
\(\Rightarrow\) se requiere un descriptor de features distintivo (e invariante a cambios geométricos y de iluminación)
?
Consideración 2: debe poderse hacer la correspondencia del mismo punto en ambas imágenes
¿Cuál corresponde a cuál?
\(\Rightarrow\) se requiere un descriptor de features distintivo (e invariante a cambios geométricos y de iluminación)
?
feature = keypoint + descriptor
Consideración 2: debe poderse hacer la correspondencia del mismo punto en ambas imágenes
¿Cuál corresponde a cuál?
\(\Rightarrow\) se requiere un descriptor de features distintivo (e invariante a cambios geométricos y de iluminación)
?
feature* = keypoint + descriptor
*dentro de este contexto, cambiará en el módulo de machine learning
¿Features repetibles y distintivas?
¿Features repetibles y distintivas?
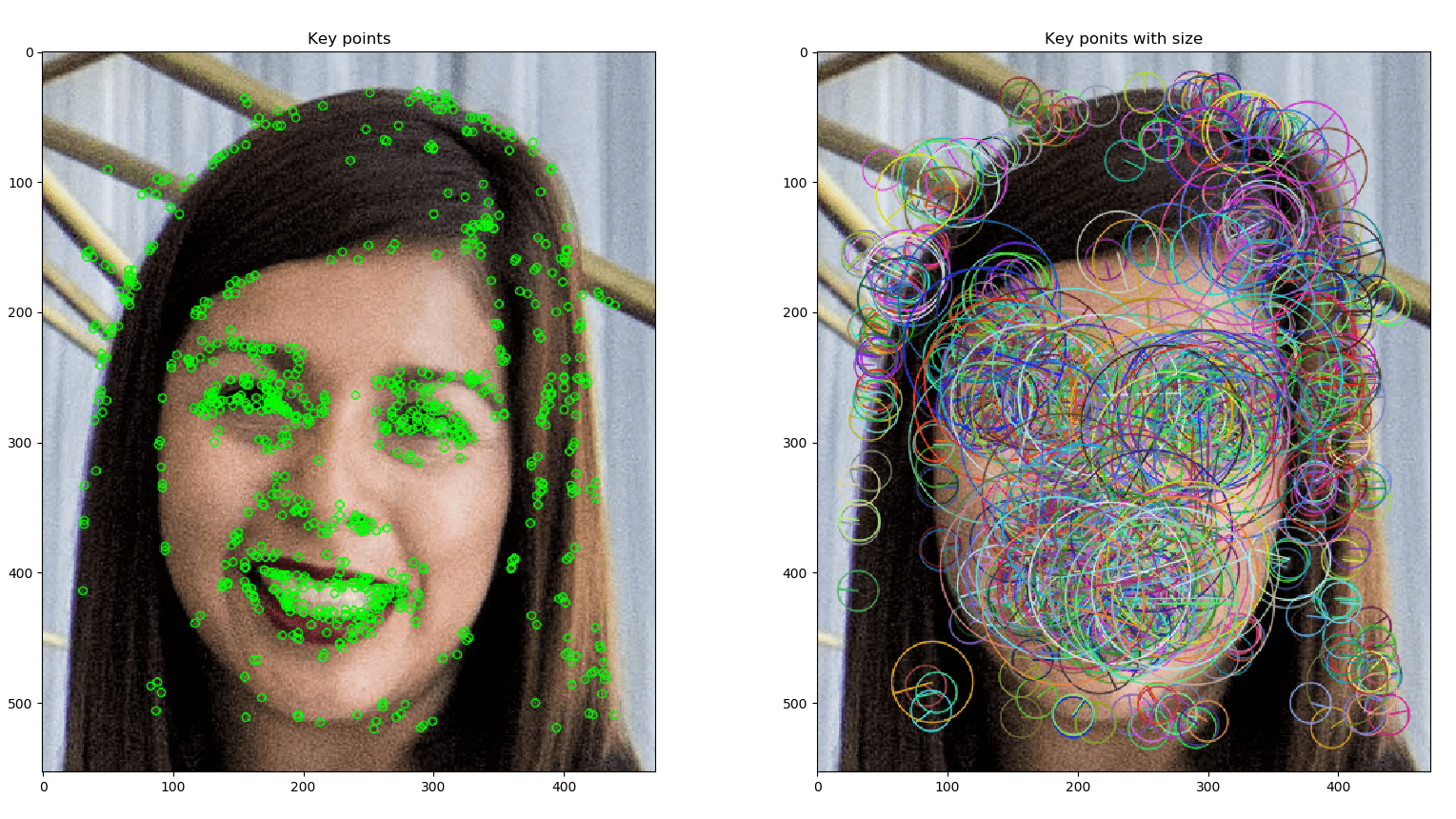
Ejemplo detector Harris (esquinas)
Ejemplo detector ORB (blobs)
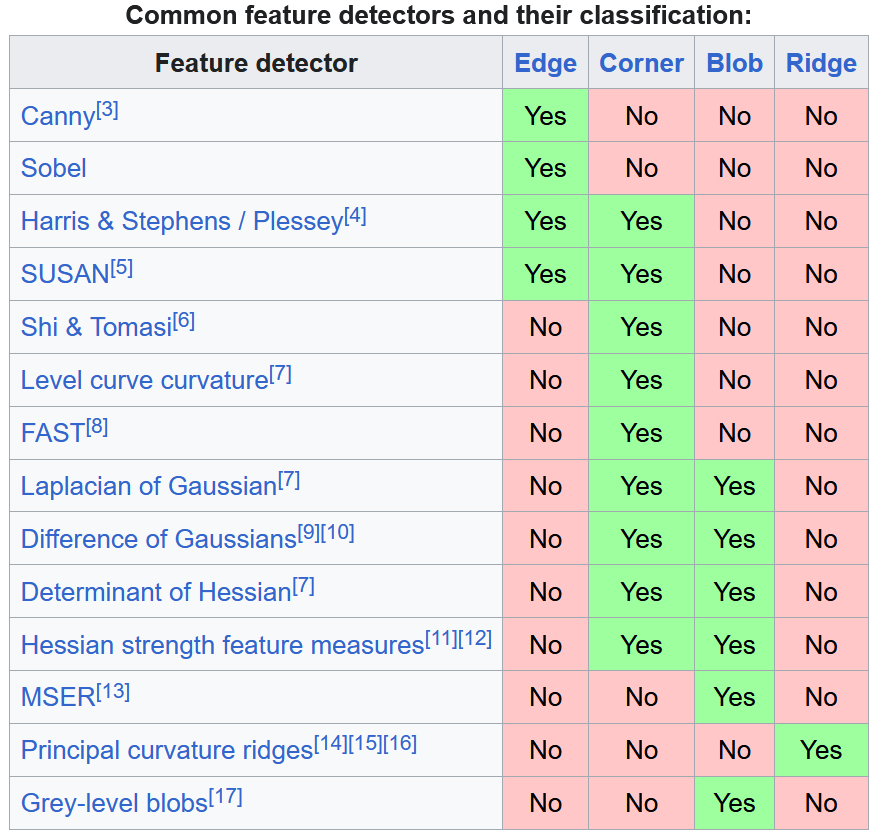
Comparación de algunos detectores
FAST
(esquinas)
ORB
(SIFT "gratis")
SIFT
(blobs)
SURF
(SIFT rápido)
Comparación de algunos detectores
FAST
(esquinas)
ORB
(SIFT "gratis")
SIFT
(blobs)
SURF
(SIFT rápido)
Regresando al ejemplo de alinear imágenes
Ejemplo: alineando dos imágenes
matching = se establecen correspondencias
Ejemplo: alineando dos imágenes
matching = se establecen correspondencias
- Brute-Force Matcher (BFMatcher en OpenCV).
- Fast Library for Approximate Nearest Neighbors (FlannBasedMatcher en OpenCV).
Ejemplo: alineando dos imágenes
>> mt3006_clase3_feature_matching.m
Ejemplo: alineando dos imágenes
correspondencias \(\to\) información requerida \(\sim\) aplicación
Ejemplo: alineando dos imágenes
correspondencias \(\to\) información requerida \(\sim\) aplicación
- Estimación de movimiento.
- Reconocimiento de objetos y lugares.
- Registro de imágenes.
- Reconstrucción 3D.
- Formación de imágenes panorámicas.
- Indexado de imágenes.
- Estéreo visión.
Referencias
- D. Scaramuzza, Vision Algorithms for Mobile Robotics, UZH: Fall 2023. https://rpg.ifi.uzh.ch/teaching.html#VAMR
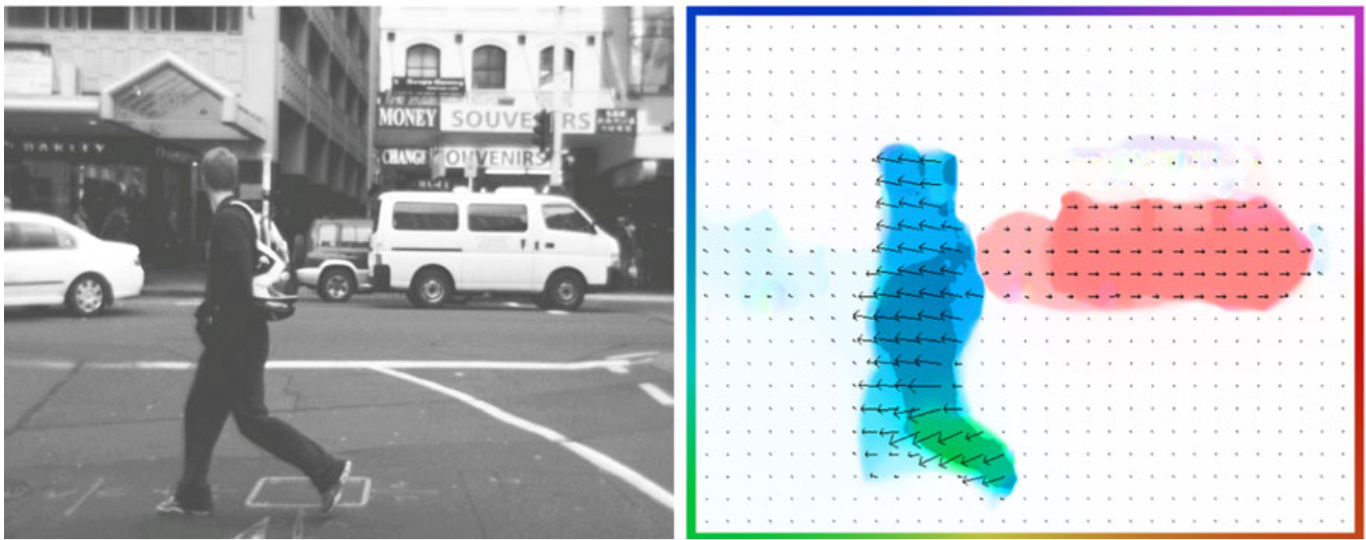
análisis (denso) de movimiento
optical flow
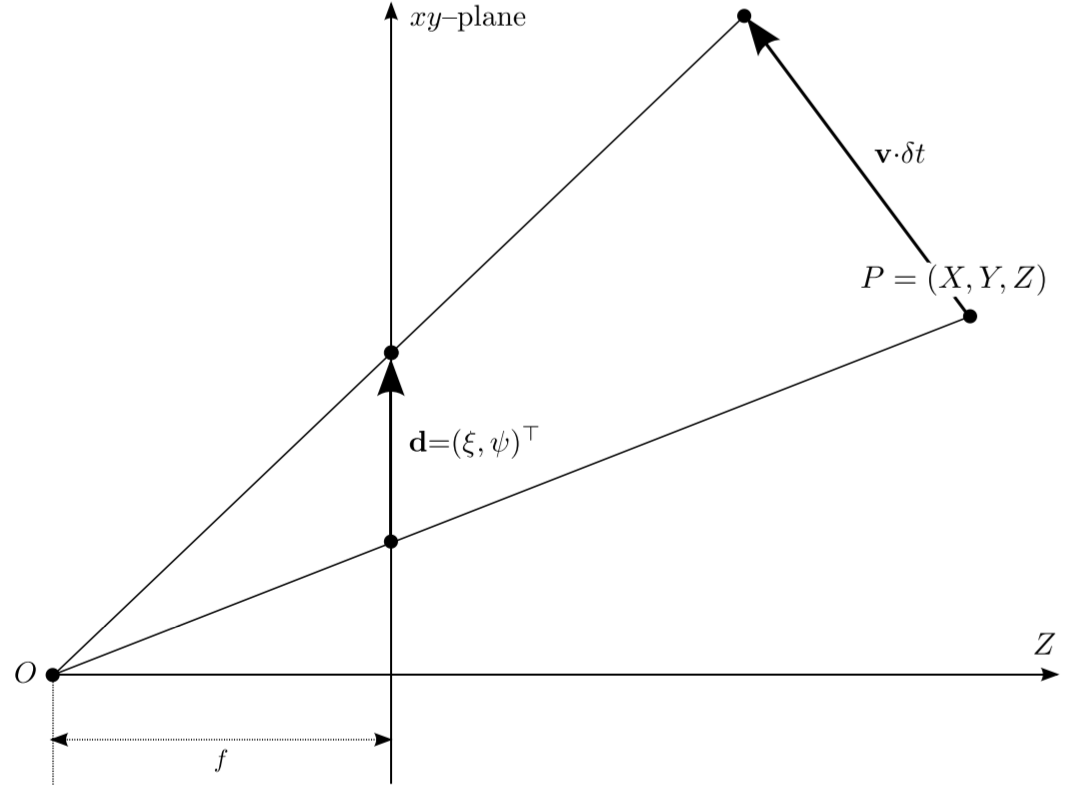
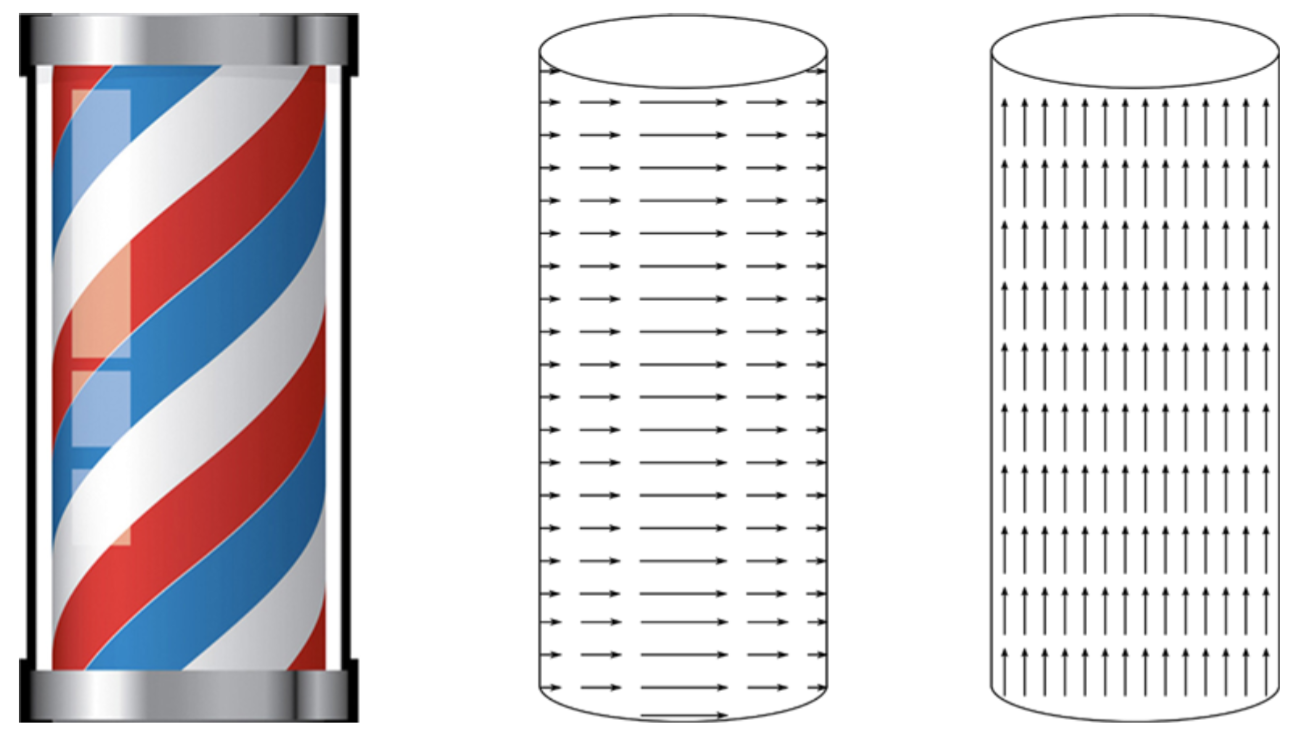
movimiento 2D
optical flow
Algoritmo de Horn-Schunk
Algoritmo de Lucas-Kanade
Algoritmo de BBPW
Feature = keypoint + descriptor
\text{descriptor} = f(\qquad)
Feature invariance
Ejemplos populares de features
FAST
ORB
SIFT
SURF
Feature matching con RANSAC
MT3006 - Lecture 3 (2024)
By Miguel Enrique Zea Arenales
