Redes neuronales profundas | Detalles de entrenamiento

MT3006 - Robótica 2

¿Por qué?

Del teorema de aproximación universal a deep learning

Deep learning vs machine learning

¿Por qué deep learning? *

¿Cuándo usar deep learning? *

SÍ

  • Gran cantidad de data       (~ 10k+ ejemplos).
  • Problema complejo.
  • Data carece de estructura.
  • Se necesita el "mejor modelo".
  • Se tiene el hardware apropiado.

NO

  • Poca data.

  • Métodos tradicionales son suficientes.

  • Data posee estructura.

  • Se posee conocimiento del dominio.

  • El modelo debe ser explicable.

¿Cuándo usar deep learning? *

SÍ

  • Gran cantidad de data       (~ 10k+ ejemplos).
  • Problema complejo.
  • Data carece de estructura.
  • Se necesita el "mejor modelo".
  • Se tiene el hardware apropiado.

NO

  • Poca data.

  • Métodos tradicionales son suficientes.

  • Data posee estructura.

  • Se posee conocimiento del dominio.

  • El modelo debe ser explicable.

* si bien esto aún es cierto, corresponde a una perspectiva anticuada.

Bajo la perspectiva de MLPs con funciones de activación ReLU puede simplemente decirse que las redes profundas son "más expresivas" que sus contrapartes no profundas.

Ejemplo de "expresividad"

x
h_1
h_2
h_3
h_1'
h_2'
h_3'
\hat{y}
h_1
h_2
h_3
h_4
h_5
h_6
\hat{y}
x

Ejemplo de "expresividad"

x
h_1
h_2
h_3
h_1'
h_2'
h_3'
\hat{y}
h_1
h_2
h_3
h_4
h_5
h_6
\hat{y}
x

7 regiones lineales     vs     16 regiones lineales

Ejemplo de "expresividad"

x
h_1
h_2
h_3
h_1'
h_2'
h_3'
\hat{y}
h_1
h_2
h_3
h_4
h_5
h_6
\hat{y}
x

7 regiones lineales     vs     16 regiones lineales

D+1
(D+1)^K

\(D\) nodos con \(K\) capas

Evaluando y ajustando modelos de machine learning

Métricas de evaluación

epoch

% accuracy

200
500
1000
100

Métricas de evaluación

epoch

% accuracy

200
500
1000
100

% de ejemplos clasificados correctamente

Métricas de evaluación

epoch

% accuracy

200
500
1000
100

% de ejemplos clasificados correctamente

¿Y para regresión?

Pueden emplearse* métricas como el MSE, RMSE y el MAE.

Métricas de evaluación

epoch

% accuracy

200
500
1000

curva plana

\(\Rightarrow\) convergencia

100

% de ejemplos clasificados correctamente

???

batches \(\mathcal{B}_r\)

batches \(\mathcal{B}_r\)

\mathbf{W}_{r+1}=\mathbf{W}_{r}-\alpha \displaystyle\sum_{i\in\mathcal{B}_r} \dfrac{\partial \ell_i(\mathbf{W}_r)}{\partial \mathbf{W}}

batch SGD

epoch

= corrida entera

batches \(\mathcal{B}_r\)

Matriz de confusión

Una forma práctica de presentar la exactitud o el error de clasificación del modelo luego de su convergencia

verdaderos positivos

verdaderos negativos

falsos negativos

clase predicha

clase real

falsos positivos

Matriz de confusión

Una forma práctica de presentar la exactitud o el error de clasificación del modelo luego de su convergencia

verdaderos positivos

verdaderos negativos

falsos negativos

clase predicha

clase real

falsos positivos

Sin embargo, sólo emplear una métrica durante el entrenamiento puede ser insuficiente para determinar el rendimiento real del modelo

Matriz de confusión

Una forma práctica de presentar la exactitud o el error de clasificación del modelo luego de su convergencia

verdaderos positivos

verdaderos negativos

falsos negativos

clase predicha

clase real

falsos positivos

Sin embargo, sólo emplear una métrica durante el entrenamiento puede ser insuficiente para determinar el rendimiento real del modelo

 

¿Por qué? Overfitting

Train-validation-test* split

Test Set*

Validation Set

Train Set

Data Set

70%

20%

10%

para entrenar el modelo

para evaluar el rendimiento y ajustar los hiperparámetros tal que se evite el overfitting

para "validar la validación" (opcional)

Train-validation-test* split

Test Set*

Validation Set

Train Set

Data Set

70%

20%

10%

para entrenar el modelo

para evaluar el rendimiento y ajustar los hiperparámetros tal que se evite el overfitting

para "validar la validación" (opcional)

parámetros del problema de optimización

Train-validation-test* split

Test Set*

Validation Set

Train Set

Data Set

70%

20%

10%

para entrenar el modelo

para evaluar el rendimiento y ajustar los hiperparámetros tal que se evite el overfitting

para "validar la validación" (opcional)

parámetros del problema de optimización

cross-validation

repite (múltiples veces) el split pero randomizando la selección de la data para el entrenamiento y la validación

Overfitting

Overfitting

¿Mejor modelo?

Overfitting

¿Mejor modelo?

explicación

+

predicción

Overfitting

mientras más data se tenga mejor podrá evaluarse el modelo

Overfitting

mientras más data se tenga mejor podrá evaluarse el modelo

Si bien esto puede evaluarse con el comportamiento de la métrica, suele hacerse con el comportamiento de la pérdida.

Ejemplos de funciones de pérdida comunes

Regresión

\dfrac{1}{n}\sum_{i=1}^{n}\left(y_i-\hat{y}_i\right)^2
\dfrac{1}{n}\sum_{i=1}^{n}\left|y_i-\hat{y}_i\right|

Error cuadrático medio (MSE) o pérdida \(\mathcal{L}_2\)

Error absoluto medio (MAE) o pérdida \(\mathcal{L}_1\)

El más fácil de emplear pero sensible a outliers.

Robusto ante outliers pero no diferenciable.

Ejemplos de funciones de pérdida comunes

Clasificación

Entropía cruzada binaria (binary cross-entropy) o pérdida logarítmica (log loss)

-\dfrac{1}{n}\sum_{i=1}^{n}\left[y_i\log\left(\hat{y}_i\right)+(1-y_i)\log\left(1-\hat{y}_i\right)\right]

Mide la "diferencia" entre dos distribuciones probabilísticas.

epoch

loss

200
500
1000

convergencia

entrenamiento

epoch

loss

200
500
1000

entrenamiento

validación

overfitting

Overfitting

Right fit

Underfitting

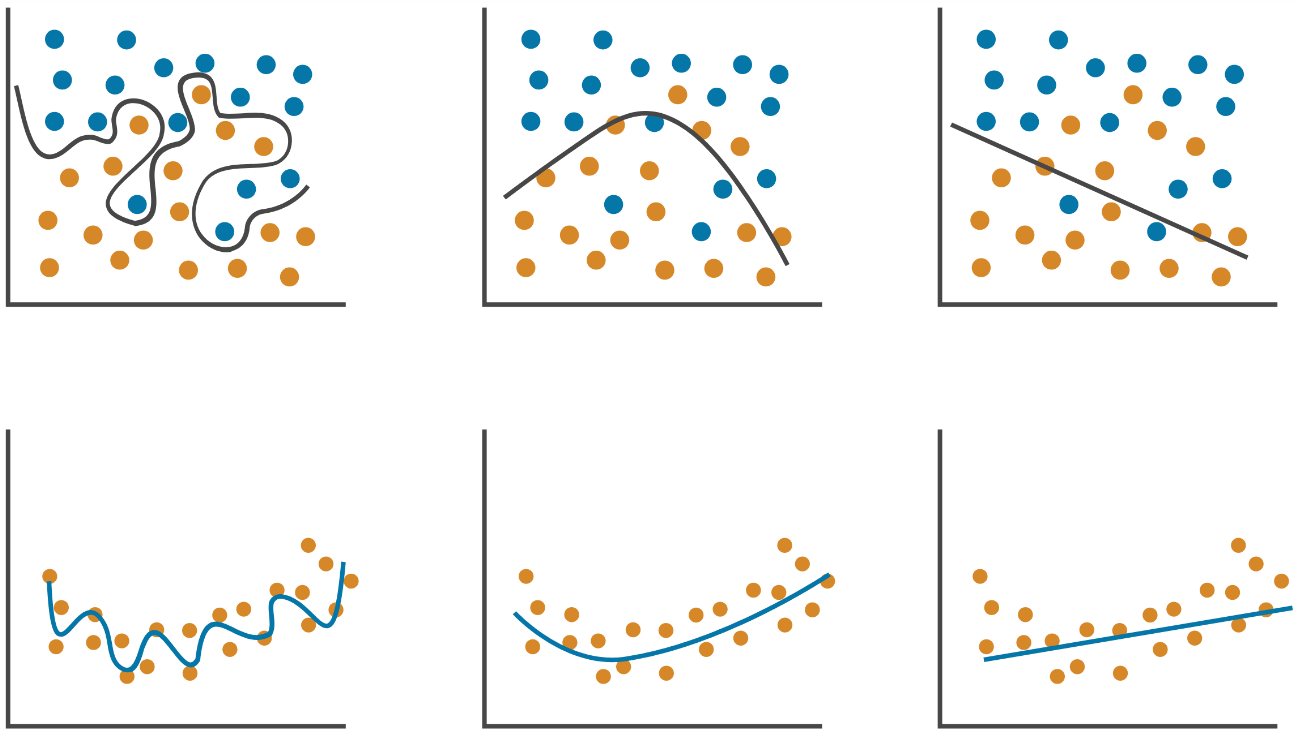
epoch

epoch

epoch

Loss

Loss

Loss

validation

training

Overfitting

Right fit

Underfitting

Overfitting

Right fit

Underfitting

epoch

epoch

epoch

Loss

Loss

Loss

validation

training

Síntomas

  • Alto sesgo (bias).
  • Alto error de entrenamiento.
  • Pérdida de entrenamiento y validación muy similares.

Síntomas

  • Pérdida de entrenamiento ligeramente menor que la de validación.

Posibles curas

  • Añadir complejidad al modelo.
  • (Añadir features).
  • Entrenar durante más tiempo.

Síntomas

  • Alta varianza.
  • Pérdida de entrenamiento baja, pero mucho más baja que la de validación.

Posibles curas

  • Obtener más data.
  • Reducir complejidad al modelo.
  • Efectuar regularización.

Regularización

Permite lidiar (hasta cierto punto) con la falta de restricciones en el problema de optimización (mediante multiplicadores de Lagrange)

\begin{aligned} \mathbf{W}^\star = \argmin_{\mathbf{W}} \quad & L(\mathbf{W}) \\ \textrm{s.t.} \quad & \text{(restricciones)} \end{aligned}

Regularización

Permite lidiar (hasta cierto punto) con la falta de restricciones en el problema de optimización (mediante multiplicadores de Lagrange)

\mathbf{W}^\star = \argmin_{\mathbf{W}} \left[ L(\mathbf{W}) + \lambda\text{(regularización)} \right]
\begin{aligned} \mathbf{W}^\star = \argmin_{\mathbf{W}} \quad & L(\mathbf{W}) \\ \textrm{s.t.} \quad & \text{(restricciones)} \end{aligned}

Ejemplo: regularización \(\mathcal{L}_2\)

\mathbf{W}^\star = \argmin_{\mathbf{W}} \left[ L(\mathbf{W}) + \lambda \displaystyle\sum_i\sum_j w_{ij}^2 \right]

Promueve pesos pequeños, por ende que el modelo sea más suave.

\|\mathbf{W}\|_F

norma (matricial) de Frobenius

Ejemplo: regularización \(\mathcal{L}_2\)

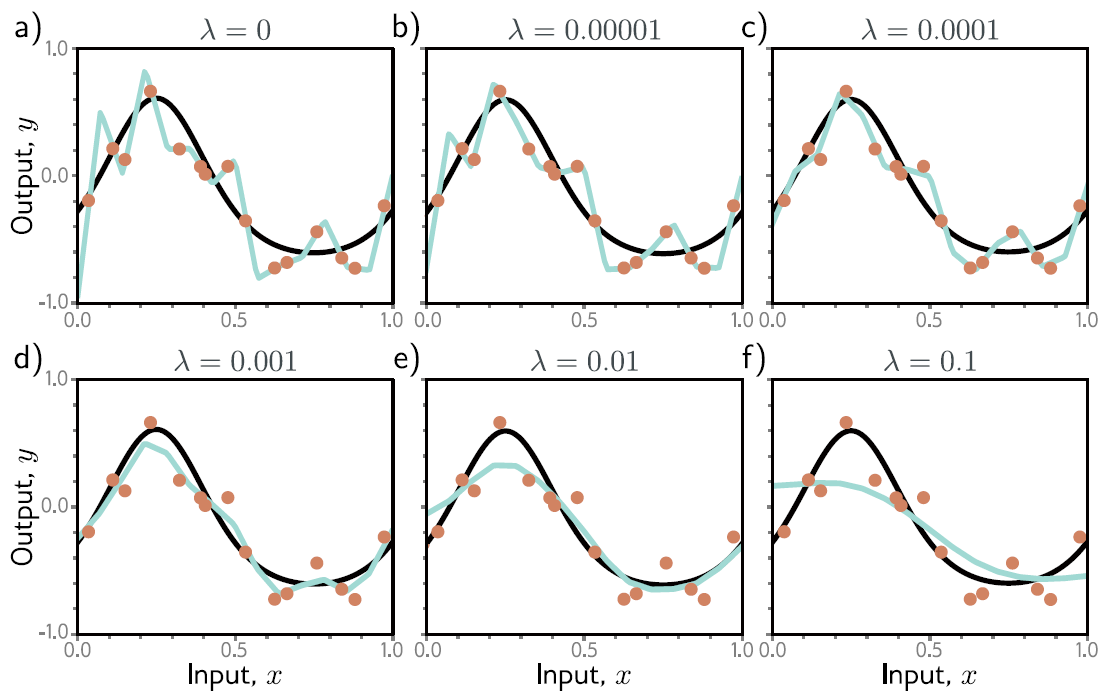
Ejemplo: regularización \(\mathcal{L}_2\)

Pueden emplearse otras normas para promover otras características, como por ejemplo escasez (sparsity) en el caso de la norma \(\mathcal{L}_1\)

Otras normas para regularización

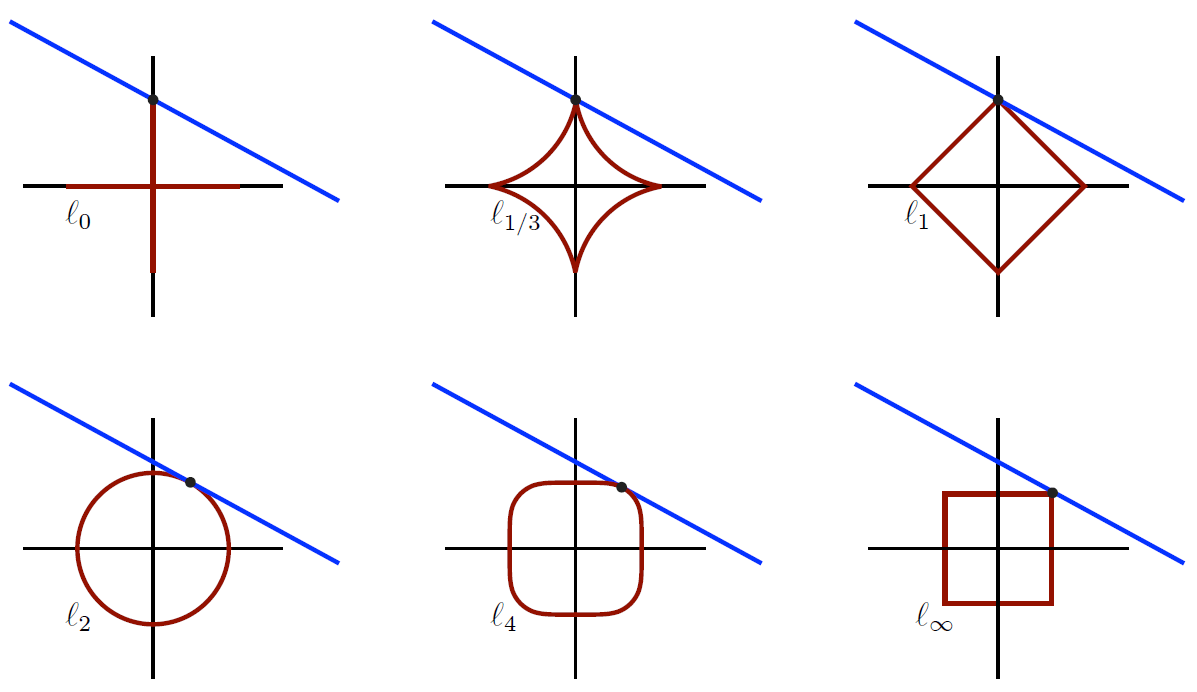
Optimizadores

\(\equiv\) modificaciones al SGD para mejorar su "convergencia"

Optimizadores

\mathbf{m}_{r+1}=\beta\mathbf{m}_r+(1-\beta)\displaystyle\sum_{i\in\mathcal{B}_r} \dfrac{\partial \ell_i(\mathbf{W}_r)}{\partial \mathbf{W}}
\mathbf{W}_{r+1}=\mathbf{W}_r-\alpha\mathbf{m}_{r+1}

Por ejemplo, puede añadirse un término de momentum para suavizar la trayectoria del SGD

\(\equiv\) modificaciones al SGD para mejorar su "convergencia"

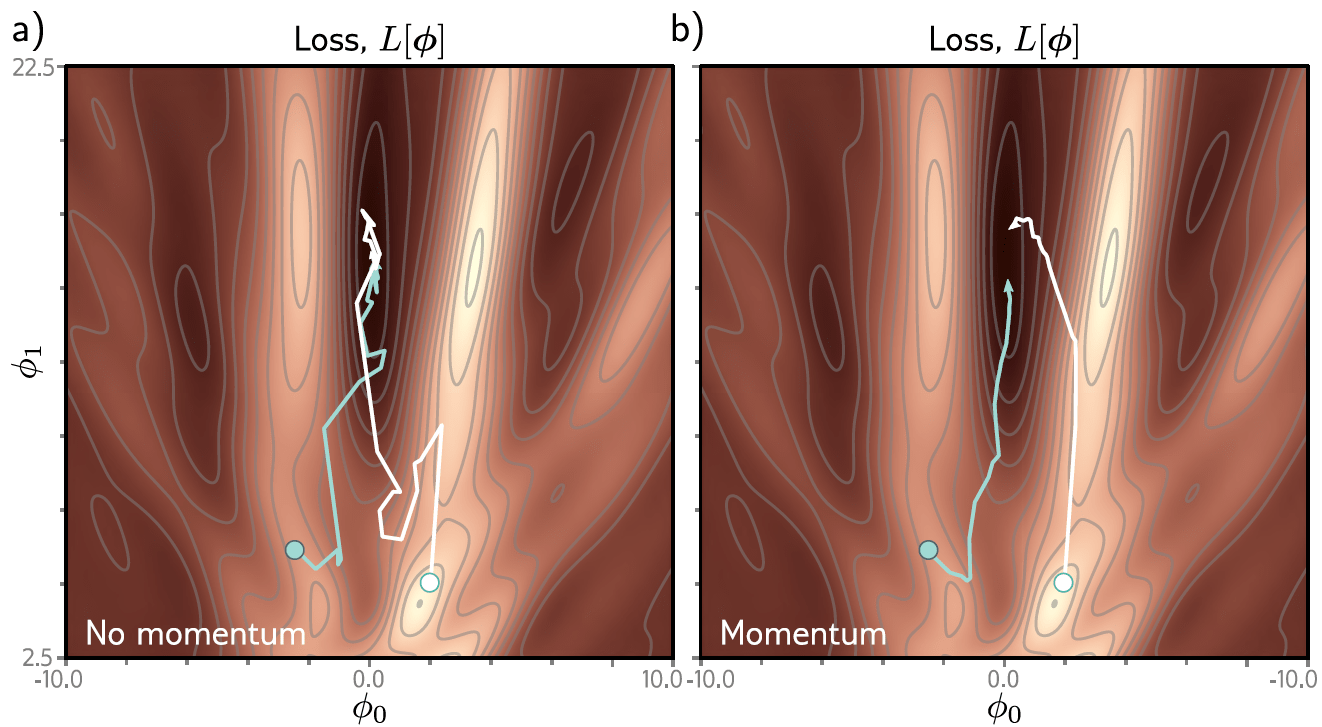
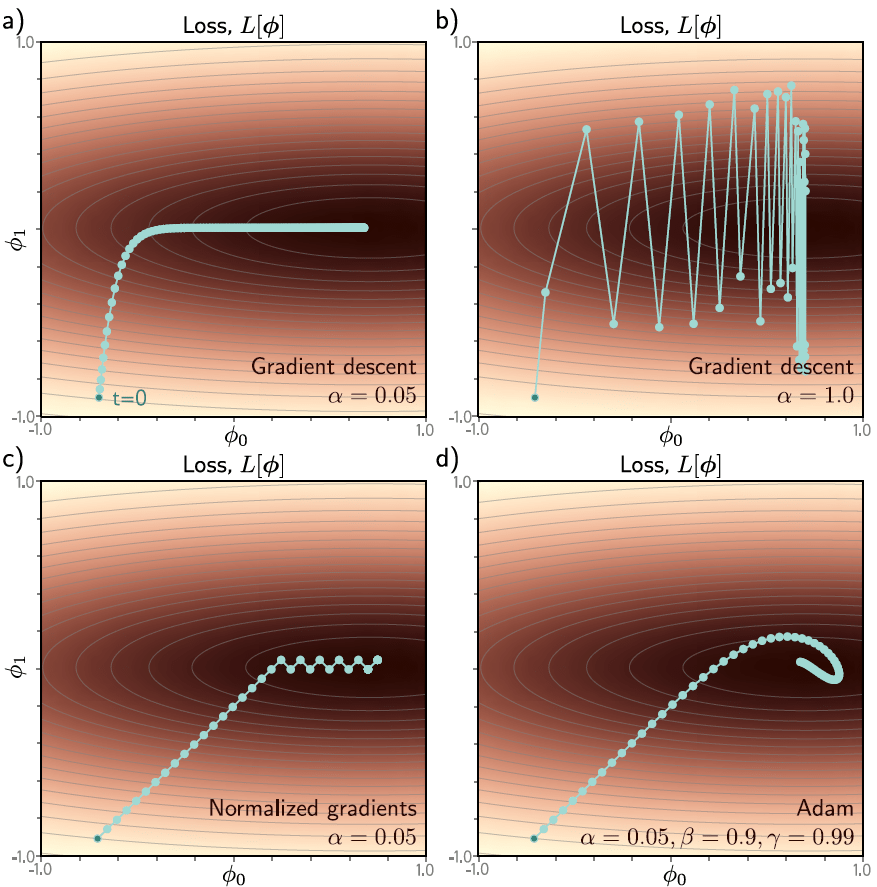
Otra modificación muy empleada es el Adaptive moment estimation (Adam) que emplea términos de momentum para el (estimado del) gradiente y el cuadrado del mismo, con el fin de obtener una convergencia suave al igual que una learning rate adaptable.

Algunos ejemplos de heurísticas que pueden apoyar al rendimiento del modelo

epoch

loss

200
500
1000

entrenamiento

validación

early stopping como una "solución" simple al overfitting

Dropout

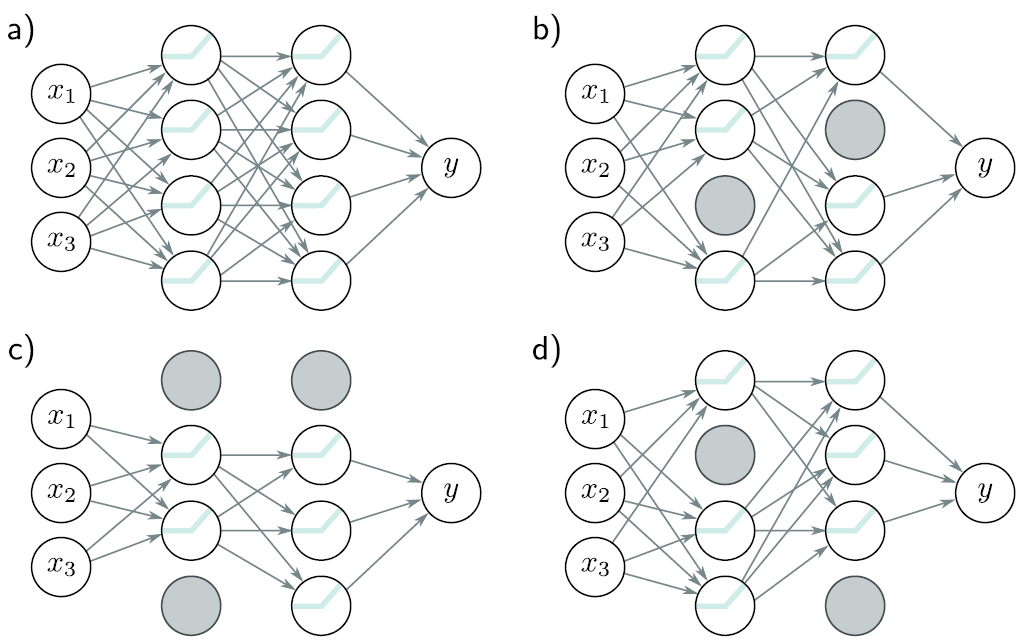
para evitar sobre dependencia de "caminos" específicos

El zoológico de redes neuronales

Frameworks para deep learning:

Un perceptrón como ejemplo

MATLAB

% Se define el modelo
net = feedforwardnet(1, 'traingdm'); % SGD con momentum
net.layers{1}.transferFcn = 'logsig'; % función de activación sigmoide

% Se establecen los hiperparámetros del modelo
net.performFcn = 'crossentropy'
net.trainParam.epochs = 100;
net.trainParam.lr = 0.1;
net.trainParam.mc = 0.9;

% Se entrena el modelo
net = train(net, X_train, y_train);

% Se hacen predicciones con el modelo
y_hat = net(X)

TensorFlow + Keras

import tensorflow as tf
from tf.keras import Sequential
from tf.keras.layers import Dense
from tf.keras.optimizers import SGD

# Se define el modelo
model = Sequential()
layer = Dense(1, activation = 'sigmoid')
model.add(layer)

# Se establecen los hiperparámetros del modelo
opt = SGD(lr = 0.1, momentum = 0.9)
model.compile(loss = 'binary_crossentropy', optimizer = opt, metrics = ['accuracy'])

# Se entrena el modelo
model.fit(X_train, y_train, epochs = 100)

# Se hacen predicciones con el modelo
y_hat = model.predict(X)

PyTorch

import torch
import torch.nn as nn
import torch.optim as optim

# Se define el modelo
class SimplePerceptron(nn.Module):
    def __init__(self, input_size):
        super(SimplePerceptron, self).__init__()
        self.output_layer = nn.Linear(input_size, 1)

    def forward(self, x):
        z = self.output_layer(x)
        y_hat = torch.sigmoid(z)
        return y_hat
      
model = SimplePerceptron(10) # tamaño de entrada de 10

# Se establecen los hiperparámetros del modelo
criterion = nn.BCELoss() # binary cross-entropy loss
optimizer = optim.SGD(model.parameters(), lr=0.1, momentum=0.9)
num_epochs = 100

# Se entrena el modelo
for epoch in range(num_epochs):
    for x, y in training_loader:
        model.train() 
        
        optimizer.zero_grad() # se establecen a cero los gradientes
        y_hat = model(x) # se calcula la salida del modelo actual
        loss = criterion(y_hat, y) # se calcula la pérdida actual

        loss.backward() # se calculan los gradientes 
        optimizer.step() # se actualizan los parámetros
        
    model.eval() # se coloca al modelo en modo de evaluación
	# SE CALCULAN LAS MÉTRICAS DE EVALUACIÓN NECESARIAS

# Se hacen predicciones con el modelo
y_hat = model(X)

>> mt3006_clase7_perceptron.py

Referencias

  1. S. Prince, Understanding Deep Learning, capítulos 4, 5, 6 y 9.

MT3006 - Lecture 7 (2024)

By Miguel Enrique Zea Arenales

MT3006 - Lecture 7 (2024)

  • 133

More from Miguel Enrique Zea Arenales