Introducción a probabilidad, variables aleatorias y procesos estocásticos
MT3006 - Robótica 2
¿Por qué?
Sensores
\ t
x(t)
\ t
x(t)
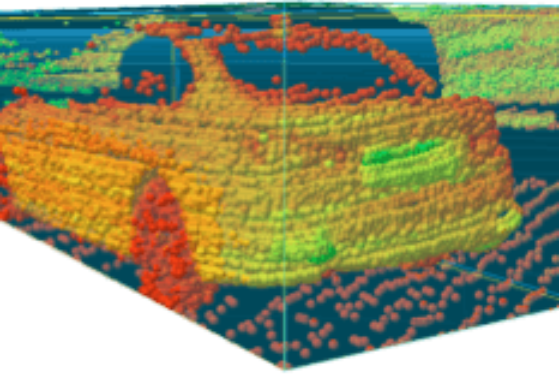
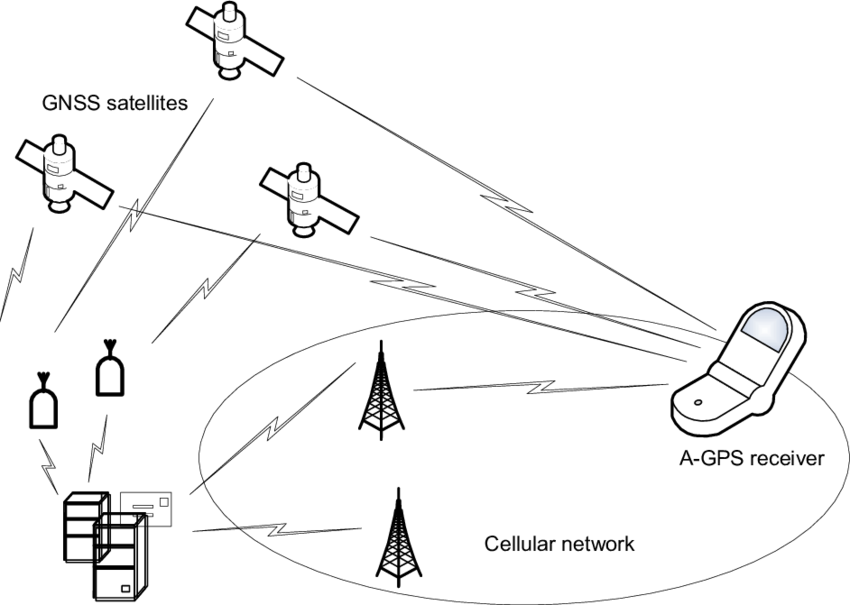
señal + ruido
\ t
x(t)
señal + ruido
aún tenemos pendiente desarrollar herramientas matemáticas para lidiar con el ruido
Probabilidad y variables aleatorias
x = -2.35893
x = -2.35893
X =
posibles valores
x = -2.35893
X =
posibles valores
existe cierta probabilidad que tome algún valor en específico dentro de los posibles
x = -2.35893
X =
posibles valores
\(\Rightarrow X\) es una variable aleatoria
existe cierta probabilidad que tome algún valor en específico dentro de los posibles
descrita por una función de densidad probabilística (pdf)
\(P(X=x)=f_X(x)\) tal que \(\displaystyle\int_{-\infty}^{\infty}f_X(x)dx=1\)
existe cierta probabilidad que tome algún valor en específico dentro de los posibles
Ejemplo: variable aleatoria discreta
1
1/6
\ x
f_X(x)
2
3
4
5
6
Ejemplo: variable aleatoria discreta
P(X=2)=f_X(2)=1/6
P(X>3)=\displaystyle\int_{3}^{\infty}f_X(x)dx=1/2
1
1/6
\ x
f_X(x)
2
3
4
5
6
Ejemplo: variable aleatoria discreta
X \sim \mathcal{U}\{1,6\}
distribución uniforme discreta
1
1/6
\ x
f_X(x)
2
3
4
5
6
P(X=2)=f_X(2)=1/6
P(X>3)=\displaystyle\int_{3}^{\infty}f_X(x)dx=1/2
Ejemplo: distribución uniforme continua
a
b
\dfrac{1}{b-a}
\ x
f_X(x)
X \sim \mathcal{U}(a,b)
P(X=2)=\mathrm{cte.}
P(X=4.75)=\mathrm{cte.}
a
b
\dfrac{1}{b-a}
\ x
X \sim \mathcal{U}(a,b)
P(X=2)=\mathrm{cte.}
P(X=4.75)=\mathrm{cte.}
X \sim \mathcal{U}(2,8)
=2
=8
=\dfrac{1}{6}
Ejemplo: distribución uniforme continua
f_X(x)
Ejemplo: distribución normal (Gaussiana)
\ x
f_X(x)
X \sim \mathcal{N}\left(\mu,\sigma^2\right)
\mu
media o promedio
\sigma^2
varianza o el cuadrado de la desviación estándar
Ejemplo: distribución normal (Gaussiana)
\ x
f_X(x)
\mu
media o promedio
\sigma^2
varianza o el cuadrado de la desviación estándar
f_X(x)=\dfrac{1}{\sigma\sqrt{2\pi}}e^{-\frac{1}{2}\left(\frac{x-\mu}{\sigma}\right)^2}
Ejemplo: distribución normal (Gaussiana)
\ x
f_X(x)
X \sim \mathcal{N}\left(0,1\right)
distribución normal estándar
-1
1
0
Ejemplo: distribución normal (Gaussiana)
\ x
-1
1
0
a veces se busca pero la probabilidad acumulada hasta cierto valor
P(X\le -1)=F_X(-1)
F_X(x)=\displaystyle\int_{-\infty}^{x}f_X(s)ds
cdf
f_X(x)
X \sim \mathcal{N}\left(0,1\right)
distribución normal estándar
Otras distribuciones
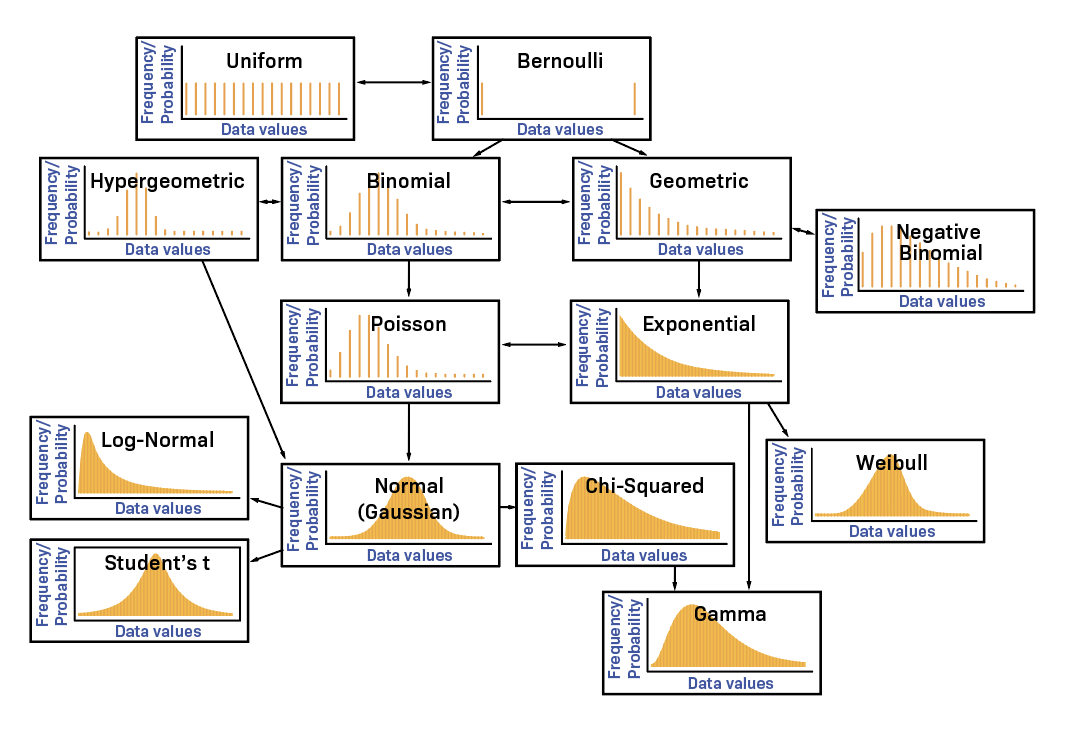
Múltiples variables aleatorias
supongamos que ahora se tienen dos variables aleatorias \(X\) y \(Y\), entonces, se define su distribución de probabilidad conjunta (joint pdf) como
P(X=x, Y=y)=f_{XY}(x,y)
P(X=x, Y=y)=f_{XY}(x,y)
sí y sólo si \(X\) y \(Y\) son independientes
f_{XY}(x,y)=f_X(x)f_Y(y)
supongamos que ahora se tienen dos variables aleatorias \(X\) y \(Y\), entonces, se define su distribución de probabilidad conjunta (joint pdf) como
Múltiples variables aleatorias
Probabilidad conjunta
toda probabilidad conjunta puede descomponerse en el producto de una probabilidad condicional con una probabilidad marginal
P(X=x, Y=y)=P(Y=y|X=x)P(X=x) \\
=P(X=x | Y=y)P(Y=y)
Probabilidad conjunta
toda probabilidad conjunta puede descomponerse en el producto de una probabilidad condicional con una probabilidad marginal
P(X=x, Y=y)=P(Y=y|X=x)P(X=x) \\
=P(X=x | Y=y)P(Y=y)
Distribución marginal
corresponde a la probabilidad que una variable tome cierto valor, independiente del valor de la(s) restante(s)
P(X=x)=f_X(x)=\int_{-\infty}^{\infty} f_{XY}(x,y) dy \\
=\int_{-\infty}^{\infty} f_{X|Y}(x,y) f_Y(y) dy
f_X(x)
(distribución) marginal de \(X\)
f_{XY}(x,y)
distribución conjunta
Distribución marginal
f_Y(y)
(distribución) marginal de \(Y\)
Probabilidad condicional y Bayes
la descomposición de la probabilidad conjunta nos permite llegar a la regla de Bayes
P(X=x|Y=y)=\dfrac{P(X=x,Y=y)}{P(Y=y)}
P(X=x|Y=y)=\dfrac{P(Y=y|X=x)P(X=x)}{P(Y=y)}
Probabilidad condicional y Bayes
P(X=x|Y=y)=\dfrac{P(Y=y|X=x)P(X=x)}{P(Y=y)}
la descomposición de la probabilidad conjunta nos permite llegar a la regla de Bayes
P(X=x|Y=y)=\dfrac{P(X=x,Y=y)}{P(Y=y)}
esta regla nos presenta una manera de actualizar el grado de creencia sobre un evento o hipótesis, dada nueva evidencia (data)
Probabilidad condicional y Bayes
P(X=x|Y=y)=\dfrac{P(Y=y|X=x)P(X=x)}{P(Y=y)}
la descomposición de la probabilidad conjunta nos permite llegar a la regla de Bayes
P(X=x|Y=y)=\dfrac{P(X=x,Y=y)}{P(Y=y)}
prior: grado de creencia sobre la hipótesis antes de considerar la evidencia (u observar la data)
Probabilidad condicional y Bayes
P(X=x|Y=y)=\dfrac{P(Y=y|X=x)P(X=x)}{P(Y=y)}
la descomposición de la probabilidad conjunta nos permite llegar a la regla de Bayes
P(X=x|Y=y)=\dfrac{P(X=x,Y=y)}{P(Y=y)}
likelihood: probabilidad que observar la evidencia (o data), dada la hipótesis
Probabilidad condicional y Bayes
P(X=x|Y=y)=\dfrac{P(Y=y|X=x)P(X=x)}{P(Y=y)}
la descomposición de la probabilidad conjunta nos permite llegar a la regla de Bayes
P(X=x|Y=y)=\dfrac{P(X=x,Y=y)}{P(Y=y)}
marginal likelihood: probabilidad de observar la evidencia (o data), bajo cualquier hipótesis
Probabilidad condicional y Bayes
P(X=x|Y=y)=\dfrac{P(Y=y|X=x)P(X=x)}{P(Y=y)}
la descomposición de la probabilidad conjunta nos permite llegar a la regla de Bayes
P(X=x|Y=y)=\dfrac{P(X=x,Y=y)}{P(Y=y)}
posterior: grado de creencia sobre la hipótesis, actualizado luego de considerar la evidencia (u observar la data)
Ejemplo: regla de Bayes
\(X:\) tasas de café al día
\(Y:\) horas de productividad
| X / Y | 0 (horas) | 1 (horas) | 2 (horas) |
| 0 (tazas) | 0.15 | 0.10 | 0.05 |
| 1 (tazas) | 0.10 | 0.15 | 0.05 |
| 2 (tazas) | 0.05 | 0.10 | 0.25 |
Ejemplo: regla de Bayes
- ¿Marginales?
- Partiendo de la probabilidad conjunta, ¿Cuál es la probabilidad que haya tomado 2 tazas de café si logré 2 horas de productividad?
- Empleando la respuesta anterior, ¿Cuál es la probabilidad que sea productivo durante 2 horas si tomé dos tazas de café?
Medidas, momentos y valor esperado
Medidas, momentos y valor esperado
Medidas, momentos y valor esperado
La media y la varianza describen a las distribuciones normales, sin embargo, resulta que forman parte de un conjunto de medidas que aplica a cualquier tipo de distribución.
La mayoría requiere de la noción general de valor esperado para calcularse.
E_X[x]=\displaystyle\int_{-\infty}^{\infty}xf_X(x)dx
\mu_X=E_X[x]
\sigma_X^2=E_X\left[(x-\mu_X)^2\right]
\rho_{XY}=\dfrac{\sigma_{XY}}{\sigma_X\sigma_Y}
\sigma_{XY}=E_{XY}\left[(x-\mu_X)(y-\mu_Y)\right]
valor esperado (promedio ponderado)
covarianza
correlación
varianza
media
Otras medidas
\mathrm{mode}=\argmax_x f_X(x)
\lim_{x \to m^-} F_X(x) \le \dfrac{1}{2} \le F_X(m)
(m)
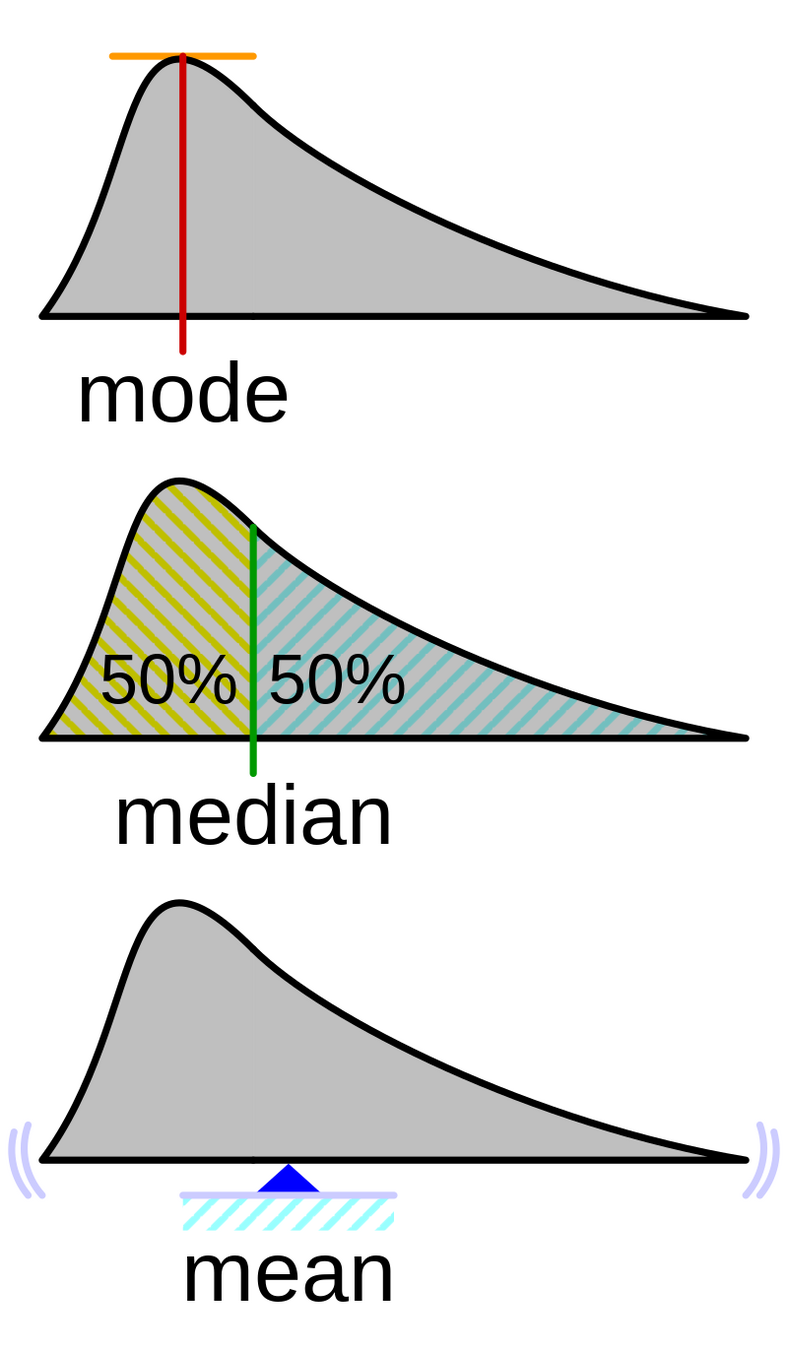
estas reciben el nombre de medidas de tendencia central
Varianza vs covarianza
>> mt3006_clase9_gaussianas.m
mientras la varianza es una medida de dispersión, la covarianza (y correlación) es una medida que representa la relación lineal entre las variables aleatorias, es decir, en qué medida el cambio de una está relacionado con el de la otra
Vectores de variables aleatorias
para evitar la confusión con matrices, emplearemos una notación distinta para vectores de variables aleatorias, por ejemplo, para el caso con \(\mathbf{x}\in\mathbb{R}^n\)
\boldsymbol{\mu}_\mathbf{x}=E\left\{\mathbf{x}\right\}=E\left\{\begin{bmatrix} x_1 \\ x_2 \\ \vdots \\ x_n \end{bmatrix}\right\}
=\begin{bmatrix} E\{x_1\} \\ E\{x_2\} \\ \vdots \\ E\{x_n\} \end{bmatrix}
adicionalmente, las varianzas y covarianzas se combinan en un único objeto denominado matriz de covarianza
\mathbf{Q}_\mathbf{x}=\mathbf{Q}^\top_\mathbf{x}=E\left\{(\mathbf{x}-\mu_\mathbf{x})(\mathbf{x}-\mu_\mathbf{x})^\top\right\}
varianzas en la diagonal y covarianzas fuera de la diagonal
Vectores de variables aleatorias
Ejemplo: Gaussiana de 3 dimensiones
\mathbf{x}=\begin{bmatrix} x_1 \\ x_2 \\ x_3 \end{bmatrix} \begin{matrix} \sim \mathcal{N}(0,1) \\ \sim \mathcal{N}(0,1) \\ \sim \mathcal{N}(0,1) \end{matrix}
\Rightarrow \mathbf{x}\sim\mathcal{N}\left(\mathbf{0}, \mathbf{Q}_\mathbf{x}\right)
f(\mathbf{x})=\dfrac{1}{\sqrt{(2\pi)^n\det(\mathbf{Q}_\mathbf{x})}}e^{-\frac{1}{2}(\mathbf{x}-\boldsymbol{\mu})^\top\mathbf{Q}_\mathbf{x}^{-1}(\mathbf{x}-\boldsymbol{\mu})}
\mathbf{Q}_\mathbf{x}=E\left\{(\mathbf{x}-\mathbf{0})(\mathbf{x}-\mathbf{0})^\top\right\}=E\left\{\mathbf{x}\mathbf{x}^\top\right\}
\mathbf{Q}_\mathbf{x}=E\left\{ \begin{bmatrix} x_1^2 & x_1x_2 & x_1x_3 \\ x_2x_1 & x_2^2 & x_2x_3 \\ x_3x_1 & x_3x_2 & x_3^2 \end{bmatrix} \right\}
Ejemplo: Gaussiana de 3 dimensiones
\mathbf{Q}_\mathbf{x}=E\left\{(\mathbf{x}-\mathbf{0})(\mathbf{x}-\mathbf{0})^\top\right\}=E\left\{\mathbf{x}\mathbf{x}^\top\right\}
\mathbf{Q}_\mathbf{x}=\begin{bmatrix} E\{x_1^2\} & E\{x_1x_2\} & E\{x_1x_3\} \\
E\{x_2x_1\} & E\{x_2^2\} & E\{x_2x_3\} \\
E\{x_3x_1\} & E\{x_3x_2\} & E\{x_3^2\} \end{bmatrix}
Ejemplo: Gaussiana de 3 dimensiones
\mathbf{Q}_\mathbf{x}=E\left\{(\mathbf{x}-\mathbf{0})(\mathbf{x}-\mathbf{0})^\top\right\}=E\left\{\mathbf{x}\mathbf{x}^\top\right\}
\mathbf{Q}_\mathbf{x}=\begin{bmatrix} \sigma_{x_1}^2 & \sigma_{x_1x_2} & \sigma_{x_1x_3} \\
\sigma_{x_1x_2} & \sigma_{x_2}^2 & \sigma_{x_2x_3} \\
\sigma_{x_1x_3} & \sigma_{x_2x_3} & \sigma_{x_3}^2 \end{bmatrix}
varianzas y el resto son covarianzas
Ejemplo: Gaussiana de 3 dimensiones
Procesos estocásticos
proceso estocástico \(x(t)\) \(\approx\) generador de variables aleatorias en el tiempo
x(t_1)\sim \mathcal{N}(0, \sigma^2)
x(t_2)\sim \mathcal{U}(0, 1)
x(t_3)\sim \mathcal{N}(10, 2\sigma^2)
x(t_4)\sim \chi^2(k)
\cdots
proceso estocástico \(x(t)\) \(\approx\) generador de variables aleatorias en el tiempo
proceso estocástico \(x(t)\) \(\approx\) generador de variables aleatorias en el tiempo
x(t_1)\sim \mathcal{N}(0, \sigma^2)
x(t_2)\sim \mathcal{U}(0, 1)
x(t_3)\sim \mathcal{N}(10, 2\sigma^2)
x(t_4)\sim \chi^2(k)
\cdots
demasiado complicado, quisiéramos que las variables salgan del mismo tipo de distribución con por lo menos la misma media
E\left\{x(t_1)\right\}=E\left\{x(t_2)\right\}=\cdots
antes de simplificar necesitamos definir
r_{xx}(t_1,t_2)=E\left\{x(t_1)x(t_2)\right\}
k_{xx}(t_1,t_2)=E\left\{(x(t_1)-\mu_{t_1})(x(t_2)-\mu_{t_2})\right\}
auto-correlación
auto-covarianza
Procesos WSS
un proceso estocástico es (weak o) wide-sense stationary si cumple con
E\left\{x(t_1)\right\}=E\left\{x(t_2)\right\}=\cdots=\mu_x
r_{xx}(t_1,t_2)=r_{xx}(t, t+\tau) \triangleq r_{xx}(\tau)
E\left\{|x(t)|^2\right\} < \infty
Procesos WSS
un proceso estocástico es (weak o) wide-sense stationary si cumple con
E\left\{x(t_1)\right\}=E\left\{x(t_2)\right\}=\cdots=\mu_x
r_{xx}(t_1,t_2)=r_{xx}(t, t+\tau) \triangleq r_{xx}(\tau)
E\left\{|x(t)|^2\right\} < \infty
Nota: el procesamiento de señales estocásticas usa la auto-correlación como la señal de tiempo y aplica (casi) los mismos métodos. Por ejemplo:
R_{xx}(\jmath\Omega)=\mathcal{F}\left\{r_{xx}(\tau)\right\}
Power Spectral Density (PSD)
Ejemplo: ruido blanco
ruido Gaussiano no correlacionado
Ejemplo: ruido blanco
ruido Gaussiano no correlacionado
r_{xx}(\tau)=\delta(\tau)
\ \tau
conocer algo del proceso en el tiempo \(t_1\) no nos dice nada sobre el proceso en el tiempo \(t_2\)
>> mt3006_clase9_ruidoblanco.m
MT3006 - Lecture 9 (2024)
By Miguel Enrique Zea Arenales
