Bitwise Manipulation and Masks
Lesson Objectives
•Perform logical, arithmetic and circular shifts on binary data
•Perform bitwise operations AND, OR and XOR
•Use masks to manipulate bits
Binary Shifts
- The ability to manipulate individual bits in a byte is one of the advantages of assembly language
- Bits can be manipulated in two ways:
- Using shift instructions to move bits left or right
- Using logical instructions NOT, AND, OR and XOR with appropriate masks
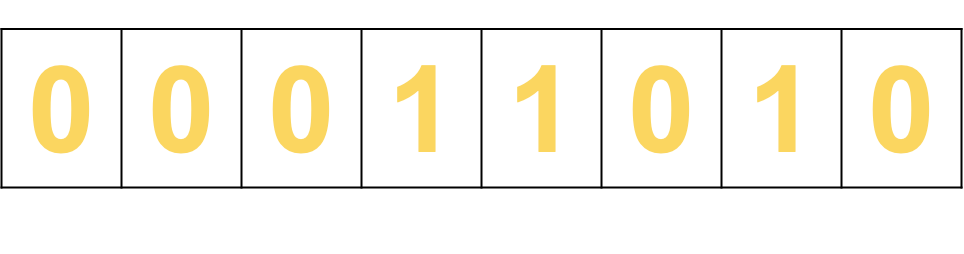
Logical Shift Right
A logical shift to the right will cause the Least Significant Bit (LSB) to be moved into the carry bit.
The Most Significant Bit (MSB) will then be padded out with a 0.
| 0 | 1 | 0 | 0 | 1 | 1 | 1 | 1 |
|---|
| 0 | 0 | 1 | 0 | 0 | 1 | 1 | 1 |
|---|
Before
Carry bit
After
| 1 |
|---|
Carry bit
Shift right 1 place:
What is the result after shifting 2 more places?
| 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 |
|---|
1
Logical Shift Left
A logical shift to the left will cause the Most Significant Bit (MSB) to be moved into the carry bit.
A zero will be carried into the LSB.
| 0 | 1 | 1 | 1 | 1 | 1 | 0 | 1 |
|---|
| 1 | 1 | 1 | 1 | 1 | 0 | 1 | 0 |
|---|
Before
Carry bit
After
| 0 |
|---|
Carry bit
Shift left 1 place:
Uses of a Logical Shift
- A logical right shift can be used to examine the least significant bit of a number.
- After the operation, the carry bit can be tested and a conditional branch executed
- Shifting left has the effect of multiplying a positive digit by 2
- However, that won’t work with a two’s complement negative number – why not?
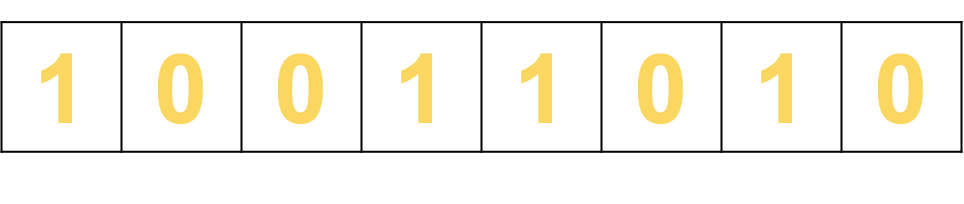
Logical Shift vs Arithmetic Shift
Arithmetic Shift
An arithmetic shift can be used to multiple or divide a binary number, for example:
If you were to apply a 1 place left shift, this has the same effect as multiplying by 2.
| 0 | 0 | 0 | 1 | 0 | 1 | 1 | 0 |
|---|
= 22
Shifted one place to the left becomes:
| 0 | 0 | 1 | 0 | 1 | 1 | 0 | 0 |
|---|
= 44
What would happen if you were to shift 2 places to the left instead of 1?
Multiplication with Shifts
- Using a combination of shifts and addition, two binary numbers can be multiplied together
- Example: Multiply 17 by 5 using shifts and addition:
| Multiply 17 by 1 | 00010001 |
| Multiply 17 by 4 with 2 left shifts | 01000100 |
| Add together the results | 01010101 |
= 85
Division with Shifts
-
Note that if you divide an odd number by 2, it is rounded down
-
What is the denary value before and after an arithmetic shift right one place?
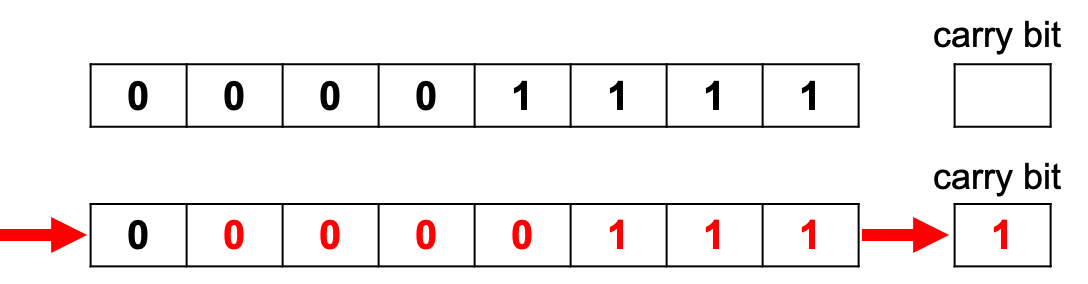
If you shift right one place and then left one place, you don’t always end up with the value you started with!
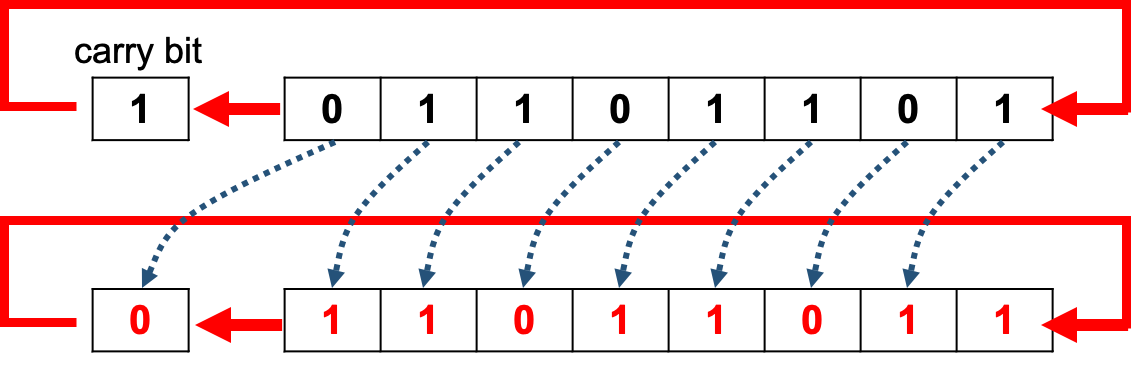
Circular Shift Right
- With a circular shift right, the carry bit is moved into the msb and the value in the lsb is moved into the carry bit
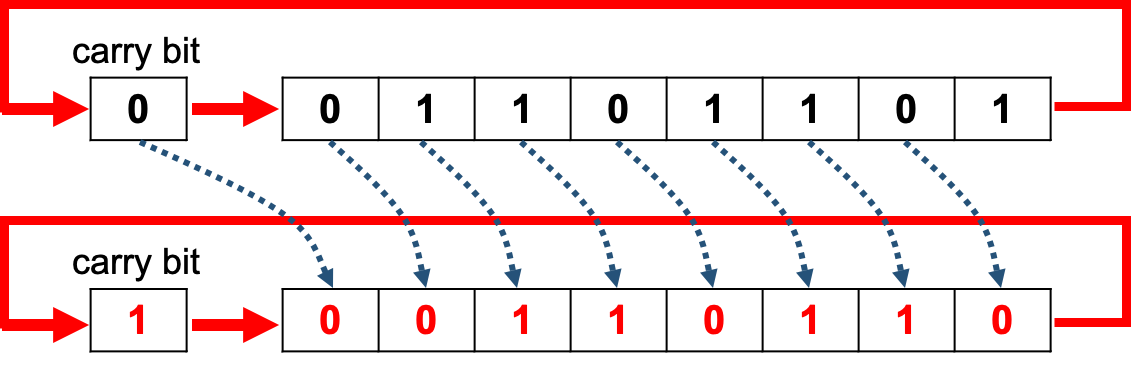
Circular Shift Left
- With a circular shift left, the value in the msb is moved into the carry bit and the carry bit into the lsb
Activity
Complete the questions in Task 1 on your worksheets.
Logical Instructions
- You have probably written programs involving complex Boolean conditions
- For example:
- If (age >= 17) and (hasLicence = True) then …
- If (temperature > 80) or (pressure > 65) then…
- In the first example, if condition A is true AND condition B is true, the complex condition is true
- In the second example, if A OR B, or both, are true, the complex condition is true
XOR
- There is another condition though, called XOR.
- XOR will only return an output if one statement is True, or if the other is True, but not when they are both True.
also called XOR
Truth Tables

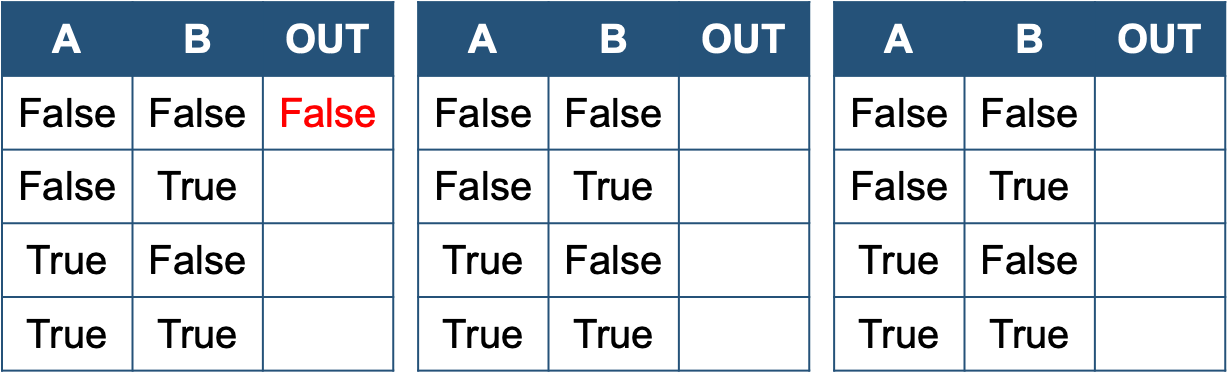
Truth Tables

Boolean Logic
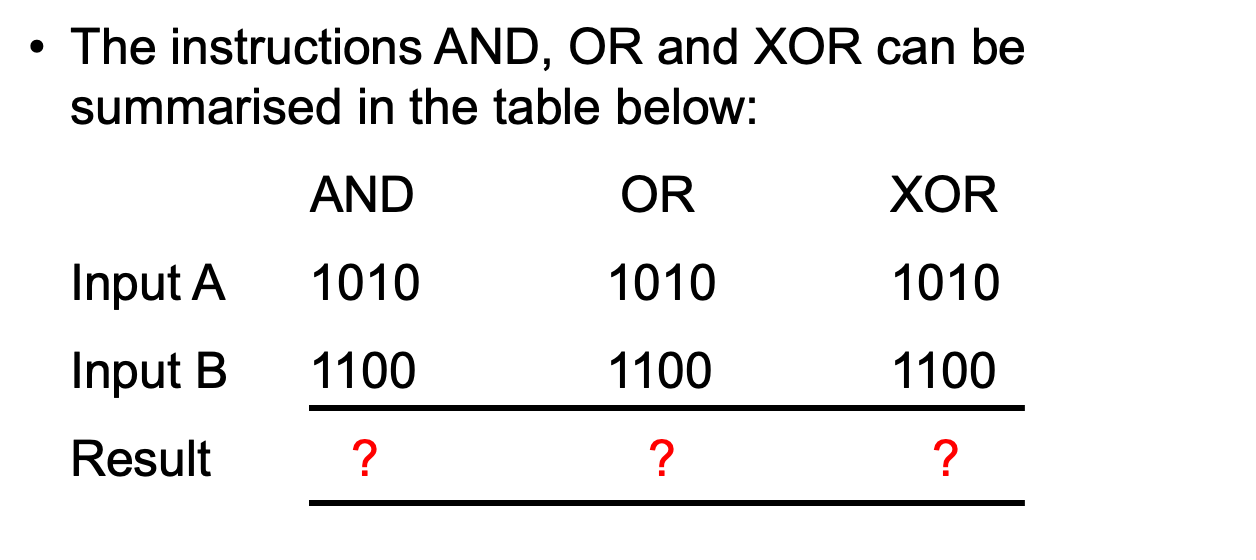
Application of AND

Application of OR

Application of XOR

Activity
Have a go at Task 2 on your worksheet
Bitwise Manipulation and Masks- Student
By CJackson
Bitwise Manipulation and Masks- Student
- 111



