Envy Free and Efficient Allocations
for Graphical Valuations
Neeldhara Misra and Aditi Sethia
The 8th International Conference on Algorithmic Decision Theory
Wed, 16th October 2024

Envy Free and Efficient Allocations
for Graphical Valuations
Outline
I. Definitions & Setup
II. Motivation and Known Results
III. Our Contributions
IV. Future Directions
Envy Free and Efficient Allocations
for Graphical Valuations
Outline
I. Definitions & Setup
II. Motivation and Known Results
III. Our Contributions
IV. Future Directions
Envy Free and Efficient Allocations
for Graphical Valuations
agents
objects



I. Definitions & Setup
Envy Free and Efficient Allocations
for Graphical Valuations



agents
objects
I. Definitions & Setup
utility

Envy Free and Efficient Allocations
for Graphical Valuations
I. Definitions & Setup

🤩

Envy Free and Efficient Allocations
for Graphical Valuations
I. Definitions & Setup
👀


Envy Free and Efficient Allocations
for Graphical Valuations
I. Definitions & Setup
😍


Envy Free and Efficient Allocations
for Graphical Valuations
I. Definitions & Setup
Envy Free and Efficient Allocations
for Graphical Valuations
I. Definitions & Setup
Valuations are additive if
\(u_k(S) = \sum_{e \in S} u_k(e)\)
Valuations are binary if
\(u_k(e) \in \{0,1\}~~\forall e\)
Valuations are identical if
\(u_k(e) = u_e~~\forall k\)
Valuations are monotone if
\(u_k(T) \leqslant u_k(S),\) for any \(T \subseteq S\)
Envy Free and Efficient Allocations
for Graphical Valuations



0
1
1
1
0
1
1
1
0
1
0
1
0
0
1
1
0
1
1
1
1
I. Definitions & Setup
Envy Free and Efficient Allocations
for Graphical Valuations



0
1
1
1
0
1
1
1
0
1
0
1
0
0
1
1
0
1
1
1
1
I. Definitions & Setup
Envy Free and Efficient Allocations
for Graphical Valuations



0
1
1
1
0
1
1
1
0
1
0
1
0
0
1
1
0
1
1
1
1
I. Definitions & Setup
I. Definitions & Setup
Envy Free and Efficient Allocations
for Graphical Valuations
Given an allocation \(X\),
if...
\(u(~~~~~) < u(~~~~~)\)





envies



I. Definitions & Setup
Envy Free and Efficient Allocations
for Graphical Valuations
Given an allocation \(X\),
if...
\(u(~~~~~) < u(~~~~~)\)





strongly
envies




I. Definitions & Setup
Envy Free and Efficient Allocations
for Graphical Valuations
Given an allocation or partial allocation \(X_1, \ldots, X_n\),
agent \(\textcolor{IndianRed}{i}\) is said to envy agent \(\textcolor{SeaGreen}{j}\) if
\[ \textcolor{IndianRed}{u_i}\left(\textcolor{IndianRed}{X_i}\right) < \textcolor{IndianRed}{u_i}\left(\textcolor{SeaGreen}{X_j}\right), \]
and agent \(\textcolor{IndianRed}{i}\) is said to strongly envy agent \(\textcolor{SeaGreen}{j}\) if
for some \(\textcolor{DodgerBlue}{x} \in \textcolor{SeaGreen}{X_j}\),
\[ \textcolor{IndianRed}{u_i}\left(\textcolor{IndianRed}{X_i}\right) < \textcolor{IndianRed}{u_i}\left(\textcolor{SeaGreen}{X_j} \setminus \{\textcolor{DodgerBlue}{x}\}\right). \]
I. Definitions & Setup
Envy Free and Efficient Allocations
for Graphical Valuations
An EFX allocation is an allocation \(X_1, \ldots, X_n\)
so that no agent strongly envies another.
For all \(i,j\), \(u_i\left(X_i\right) \geq u_i\left(X_j \backslash\{x\}\right), \forall x \in X_j\)
An EF allocation is an allocation \(X_1, \ldots, X_n\)
so that no agent envies another:
For all \(i,j\), \(u_i\left(X_i\right) \geq u_i\left(X_j\right)\)
Envy-Freeness (EF).
Envy-Freeness up to any item (EFX).
Envy Free and Efficient Allocations
for Graphical Valuations



0
1
1
1
0
1
1
1
0
1
0
1
0
0
1
1
0
1
1
1
1
I. Definitions & Setup
Envy Free and Efficient Allocations
for Graphical Valuations
if you see a matrix where every column has two ones...
...every row is a vertex and every column is an edge!

I. Definitions & Setup



0
1
1
1
0
1
1
1
0
1
0
1
0
0
1
1
0
1
1
1
1
recall the valuation matrix in our example...
Envy Free and Efficient Allocations
for Graphical Valuations
I. Definitions & Setup









0
1
1
1
0
1
1
1
0
1
0
1
0
0
1
1
0
1
1
1
1






0
1
1
1
0
1
1
1
0
1
0
1
0
0
1
1
0
1
1
1
1






0
1
1
1
0
1
1
1
0
1
0
1
0
0
1
1
0
1
1
1
1






0
1
1
1
0
1
1
1
0
1
0
1
0
0
1
1
0
1
1
1
1






0
1
1
1
0
1
1
1
0
1
0
1
0
0
1
1
0
1
1
1
1






0
1
1
1
0
1
1
1
0
1
0
1
0
0
1
1
0
1
1
1
1






0
1
1
1
0
1
1
1
0
1
0
1
0
0
1
1
0
1
1
1
1






0
1
1
1
0
1
1
1
0
1
0
1
0
0
1
1
0
1
1
1
1






0
1
1
1
0
1
1
1
0
1
0
1
0
0
1
1
0
1
1
1
1






0
1
1
1
0
1
1
1
0
1
0
1
0
0
1
1
0
1
1
1
1






0
1
1
1
0
1
1
1
0
1
0
1
0
0
1
1
0
1
1
1
1






0
1
1
1
0
1
1
1
0
1
0
1
0
0
1
1
0
1
1
1
1






0
1
1
1
0
1
1
1
0
1
0
1
0
0
1
1
0
1
1
1
1






0
1
1
1
0
1
1
1
0
1
0
1
0
0
1
1
0
1
1
1
1






0
1
1
1
0
1
1
1
0
1
0
1
0
0
1
1
0
1
1
1
1






Envy Free and Efficient Allocations
for Graphical Valuations
Envy Free and Efficient Allocations
for Graphical Valuations
I. Definitions & Setup
Envy Free and Efficient Allocations
for Graphical Valuations
I. Definitions & Setup








Envy Free and Efficient Allocations
for Graphical Valuations
Envy Free and Efficient Allocations
for Graphical Valuations
Envy Free and Efficient Allocations
for Graphical Valuations
I. Definitions & Setup
\( u_{\textcolor{SeaGreen}{k}}(X \cup \{\textcolor{IndianRed}{e}\}) = u_{\textcolor{SeaGreen}{k}}(X), \forall X \subseteq E \)
An object \({\color{IndianRed}e}\) is irrelevant to an agent \({\color{SeaGreen}k}\) if:
Envy Free and Efficient Allocations
for Graphical Valuations
If an item is not irrelevant for agent \(k\) is said to be relevant for agent \(k\).
Graphical Valuations.
Every item is relevant to at most 2 agents and
for every pair of agents there exists at most one item relevant to both of them.
Envy Free and Efficient Allocations
for Graphical Valuations
Envy Free and Efficient Allocations
for Graphical Valuations
I. Definitions & Setup
\( u_{\textcolor{SeaGreen}{k}}(X \cup \{\textcolor{IndianRed}{e}\}) = u_{\textcolor{SeaGreen}{k}}(X), \forall X \subseteq E \)
An object \({\color{IndianRed}e}\) is irrelevant to an agent \({\color{SeaGreen}k}\) if:
Envy Free and Efficient Allocations
for Graphical Valuations
This class of valuations can be represented via a graph \(G=(V, E)\)
where the vertices represent the agents, i.e., \(V=\{1, \ldots, n\}\),
and the set of edges \(E\) is the set of items, where the item represented by the edge \((i, j)\) is only relevant to both agents \(i\) and \(j\).
Envy Free and Efficient Allocations
for Graphical Valuations
I. Definitions & Setup








Envy Free and Efficient Allocations
for Graphical Valuations
I. Definitions & Setup
are orientations








some
Envy Free and Efficient allocations
for Graphical Valuations
Envy Free and Efficient Allocations
for Graphical Valuations
Outline
I. Definitions & Setup
II. Motivation and Known Results
III. Our Contributions
IV. Future Directions
Envy Free and Efficient Allocations for Graphical Valuations
II. Motivation and Known Results
EC · 2023
Envy Free and Efficient Allocations for Graphical Valuations
II. Motivation and Known Results
EC · 2023




EFX Allocations on Graphs
Example showing non-existence of EFX orientations
Envy Free and Efficient Allocations for Graphical Valuations
II. Motivation and Known Results
EC · 2023




EFX Allocations on Graphs
Example showing non-existence of EFX orientations


Envy Free and Efficient Allocations for Graphical Valuations
II. Motivation and Known Results
EC · 2023




EFX Allocations on Graphs
Example showing non-existence of EFX orientations



Envy Free and Efficient Allocations for Graphical Valuations
II. Motivation and Known Results
EC · 2023




EFX Allocations on Graphs
Example showing non-existence of EFX orientations


Envy Free and Efficient Allocations for Graphical Valuations
II. Motivation and Known Results
EC · 2023




EFX Allocations on Graphs
Example showing non-existence of EFX orientations


Envy Free and Efficient Allocations for Graphical Valuations
II. Motivation and Known Results
EC · 2023




EFX Allocations on Graphs
Example showing non-existence of EFX orientations


Envy Free and Efficient Allocations for Graphical Valuations
II. Motivation and Known Results
EC · 2023
EFX Allocations on Graphs
It is an NP-complete problem to decide whether a graph has an EFX orientation.
This remains true even for symmetric graphs.
Envy Free and Efficient Allocations for Graphical Valuations
II. Motivation and Known Results
EC · 2023
EFX Allocations on Graphs
It is an NP-complete problem to decide whether a graph has an EFX orientation.
This remains true even for symmetric graphs.
...is there a characterization of graphs that exhibit EFX orientation regardless of the assigned valuations?
Envy Free and Efficient Allocations for Graphical Valuations
II. Motivation and Known Results

Preprint · 2024
Envy Free and Efficient Allocations for Graphical Valuations
II. Motivation and Known Results
Preprint · 2024
On the Structure of EFX Orientations on Graphs
A graph is strongly EFX-orientable if,
for any assigned monotone valuation,
there exists an EFX orientation.
A graph \(G\) is 0-1 strongly EFX-orientable if,
for any assigned additive 0-1 valuation,
there exists an EFX-orientation.
Envy Free and Efficient Allocations for Graphical Valuations
II. Motivation and Known Results
Preprint · 2024
On the Structure of EFX Orientations on Graphs
Any graph of chromatic number \(\chi(G) \leqslant 2\)
is strongly EFX-orientable.
A graph is strongly EFX-orientable if,
for any assigned monotone valuation,
there exists an EFX orientation.
All strongly EFX-orientable graphs have chromatic number \(\chi(G) \leqslant 3\).
A graph is strongly EFX-orientable if,
for any assigned monotone valuation,
there exists an EFX orientation.
Envy Free and Efficient Allocations for Graphical Valuations
II. Motivation and Known Results
Preprint · 2024
On the Structure of EFX Orientations on Graphs
*There exist graphs of \(\chi(G)=3\) which are not strongly EFX-orientable,
as well as graphs with \(\chi(G)=3\) which are strongly EFX-orientable,
so this bound is sharp.
A graph is strongly EFX-orientable if,
for any assigned monotone valuation,
there exists an EFX orientation.
A graph is strongly EFX-orientable if,
for any assigned monotone valuation,
there exists an EFX orientation.
Envy Free and Efficient Allocations for Graphical Valuations
II. Motivation and Known Results
Preprint · 2024
On the Structure of EFX Orientations on Graphs
A graph \(G\) is \(0-1\) strongly EFX-orientable if and only if, for every subgraph \(H \subseteq G\) such that \(H\) is a forest consisting of trees \(T_1, T_2 \ldots T_k\),
for every \(1 \leqslant i \leqslant k\) there exists \(x_i \in T_i\)
such that \(\bigcup_{i=1}^k N_H\left(x_i\right)\) forms an independent set on \(G\),
where \(N_H(x)\) denotes the neighbors of \(x\) in \(H\).
A graph \(G\) is 0-1 strongly EFX-orientable if,
for any assigned additive 0-1 valuation,
there exists an EFX-orientation.
Envy Free and Efficient Allocations for Graphical Valuations
II. Motivation and Known Results
Preprint · 2024
On the Structure of EFX Orientations on Graphs
Any bipartite graph is strongly EFX-orientable.


Envy Free and Efficient Allocations for Graphical Valuations
II. Motivation and Known Results
Preprint · 2024
On the Structure of EFX Orientations on Graphs
Any bipartite graph is strongly EFX-orientable.


Envy Free and Efficient Allocations for Graphical Valuations
II. Motivation and Known Results
Preprint · 2024
On the Structure of EFX Orientations on Graphs
Any bipartite graph is strongly EFX-orientable.



Envy Free and Efficient Allocations for Graphical Valuations
II. Motivation and Known Results

EC · 2023
Envy Free and Efficient Allocations for Graphical Valuations
II. Motivation and Known Results
EC · 2023
EFX Allocations on Graphs
There is always an EFX allocation for graphs.
In particular this implies that there are cases
where any EFX allocation must assign items to agents for which they are irrelevant.
Envy Free and Efficient Allocations for Graphical Valuations
II. Motivation and Known Results
EC · 2023
EFX Allocations on Graphs
There is always an EFX allocation for graphs.
In particular this implies that there are cases
where any EFX allocation must assign items to agents for which they are irrelevant.
...what about EF?
...what about EFX allocations that minimize waste?


Envy Free and Efficient Allocations
for Graphical Valuations
Outline
I. Definitions & Setup
II. Motivation and Known Results
III. Our Contributions
IV. Future Directions
III. Our Contributions
Envy Free and Efficient Allocations for Graphical Valuations
Envy-free allocations
on graphical valuations.
EFX allocations that maximize welfare
on graphical valuations.
Two themes.
III. Our Contributions
Envy Free and Efficient Allocations for Graphical Valuations
Given a graphical allocation instance,
there is an EF allocation if and only if there is an EF orientation.
For \(\{0,1\}\)-graphical instances,
an EF allocation can be found efficiently, if it exists.
Deciding whether an EF allocation exists is NP-hard,
even for symmetric \(\{0,1, d\}\)-graphical valuations.
Given a graphical allocation instance
with a bounded number of distinct utilities,
the problem of finding an EF allocation is FPT
in the vertex cover number of the associated graph \(G\).
envy-freeness
III. Our Contributions
Envy Free and Efficient Allocations for Graphical Valuations
Given a graphical allocation instance,
there is an EF allocation if and only if there is an EF orientation.
envy-freeness






III. Our Contributions
Envy Free and Efficient Allocations for Graphical Valuations
Given a graphical allocation instance,
there is an EF allocation if and only if there is an EF orientation.
envy-freeness






If
envies

in the new allocation,
then

envied

in the old allocation.
III. Our Contributions
Envy Free and Efficient Allocations for Graphical Valuations
envy-freeness
For \(\{0,1\}\)-graphical instances,
an EF allocation can be found efficiently, if it exists.
When edges are asymmetric
(valued at 0 by one agent and 1 by the other),
orient them towards the agent who values the edge more.
By the previous result, it is enough to find an orientation.
When edges are symmetric 0-0,
(neither agent cares for the item in question),
orient them arbitrarily.
Left with components with 1-1 edges only: cases based on trees/non-trees.
III. Our Contributions
Envy Free and Efficient Allocations for Graphical Valuations
envy-freeness
Deciding whether an EF allocation exists is NP-hard,
even for symmetric \(\{0,1, d\}\)-graphical valuations.
By a reduction from the multi-colored independent set problem.
III. Our Contributions
Envy Free and Efficient Allocations for Graphical Valuations
envy-freeness
Deciding whether an EF allocation exists is NP-hard,
even for symmetric \(\{0,1, d\}\)-graphical valuations.
By a reduction from the multi-colored independent set problem.
III. Our Contributions
Envy Free and Efficient Allocations for Graphical Valuations
envy-freeness
Deciding whether an EF allocation exists is NP-hard,
even for symmetric \(\{0,1, d\}\)-graphical valuations.
By a reduction from the multi-colored independent set problem.
selector gadgets
one of these
heavy edges is oriented towards the global vertex in any EF orientation.
III. Our Contributions
Envy Free and Efficient Allocations for Graphical Valuations
envy-freeness
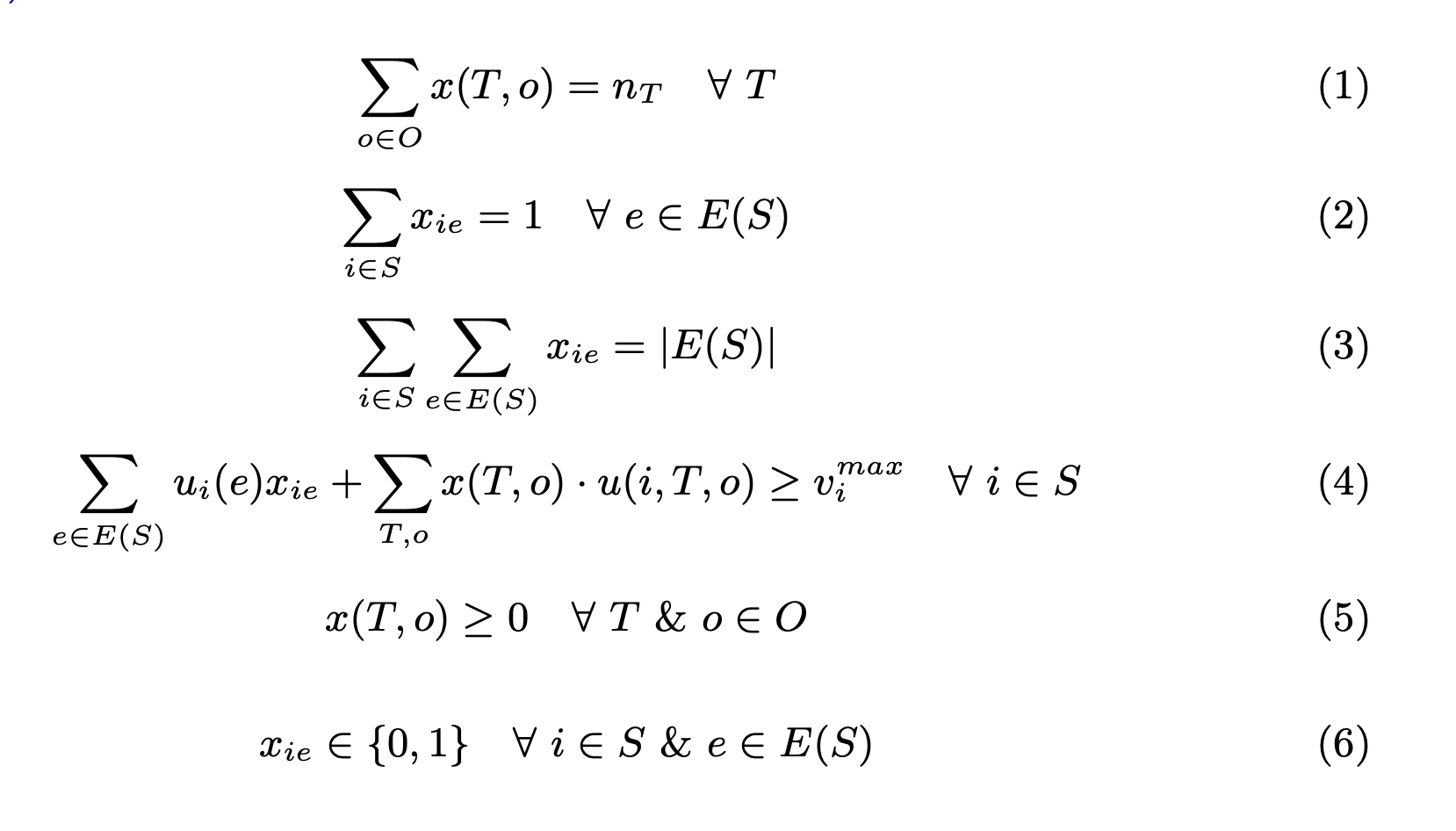
by a reduction to ILP with a small number of variables...
Given a graphical allocation instance
with a bounded number of distinct utilities,
the problem of finding an EF allocation is FPT
in the vertex cover number of the associated graph \(G\).
III. Our Contributions
Envy Free and Efficient Allocations for Graphical Valuations
For \(\{0,1\}\)-graphical instances,
a non-wasteful EFX allocation always exists and can be found in polynomial time.
Therefore, the Price of EFX with respect to Utilitarian welfare is 1.
The price of EFX with respect to Utilitarian welfare is \(\infty\)
even for \(\{0,1, d\}\)-graphical valuations.
EFX
Given an instance of graphical valuations,
deciding the existence of a utilitarian welfare-maximizing and EFX allocation (UM+EFX) is NP-Hard.
III. Our Contributions
Envy Free and Efficient Allocations for Graphical Valuations
For \(\{0,1\}\)-graphical instances,
a non-wasteful EFX allocation always exists and can be found in polynomial time.
Therefore, the Price of EFX with respect to Utilitarian welfare is 1.
EFX
A graph \(G\) is \(0-1\) strongly EFX-orientable if and only if, for every subgraph \(H \subseteq G\) such that \(H\) is a forest consisting of trees \(T_1, T_2 \ldots T_k\),
for every \(1 \leqslant i \leqslant k\) there exists \(x_i \in T_i\)
such that \(\bigcup_{i=1}^k N_H\left(x_i\right)\) forms an independent set on \(G\),
where \(N_H(x)\) denotes the neighbors of \(x\) in \(H\).
III. Our Contributions
Envy Free and Efficient Allocations for Graphical Valuations
The price of EFX with respect to Utilitarian welfare is \(\infty\)
even for \(\{0,1, d\}\)-graphical valuations.
EFX
welfare-optimal: root takes all for \(d^2\).
EFX: root cannot get more than one item; \(\leqslant d\).
d
1
1
1
1
1
III. Our Contributions
Envy Free and Efficient Allocations for Graphical Valuations
EFX
Given an instance of graphical valuations,
deciding the existence of a utilitarian welfare-maximizing and EFX allocation (UM+EFX) is NP-Hard.
Envy Free and Efficient Allocations
for Graphical Valuations
Outline
I. Definitions & Setup
II. Motivation and Known Results
III. Our Contributions
IV. Future Directions
Envy Free and Efficient Allocations for Graphical Valuations
IV. Future Directions
faster parameterized algorithms
e.g, via smaller parameters than vertex cover
Envy Free and Efficient Allocations for Graphical Valuations
IV. Future Directions
faster parameterized algorithms
e.g, via smaller parameters than vertex cover
multi-edges
we dealt with simple graphs, this allows copies of items
Envy Free and Efficient Allocations for Graphical Valuations
IV. Future Directions
faster parameterized algorithms
e.g, via smaller parameters than vertex cover
multi-edges
we dealt with simple graphs, this allows copies of items
bounded arity hyper-edges
in graphical allocations, the arity is two
Envy Free and Efficient Allocations for Graphical Valuations
IV. Future Directions
faster parameterized algorithms
e.g, via smaller parameters than vertex cover
multi-edges
we dealt with simple graphs, this allows copies of items
bounded arity hyper-edges
in graphical allocations, the arity is two
more general price of fairness results
beyond binary
Envy Free and Efficient Allocations for Graphical Valuations
IV. Future Directions
faster parameterized algorithms
e.g, via smaller parameters than vertex cover
multi-edges
we dealt with simple graphs, this allows copies of items
bounded arity hyper-edges
in graphical allocations, the arity is two
more general price of fairness results
beyond binary
empirical validation
what fraction of real-world instances are graphical?
Envy Free and Efficient Allocations for Graphical Valuations
IV. Future Directions
faster parameterized algorithms
e.g, via smaller parameters than vertex cover
multi-edges
we dealt with simple graphs, this allows copies of items
bounded arity hyper-edges
in graphical allocations, the arity is two
more general price of fairness results
beyond binary
empirical validation
what fraction of real-world instances are graphical?

ADT 2024 Talk
By Neeldhara Misra
ADT 2024 Talk
- 816



