

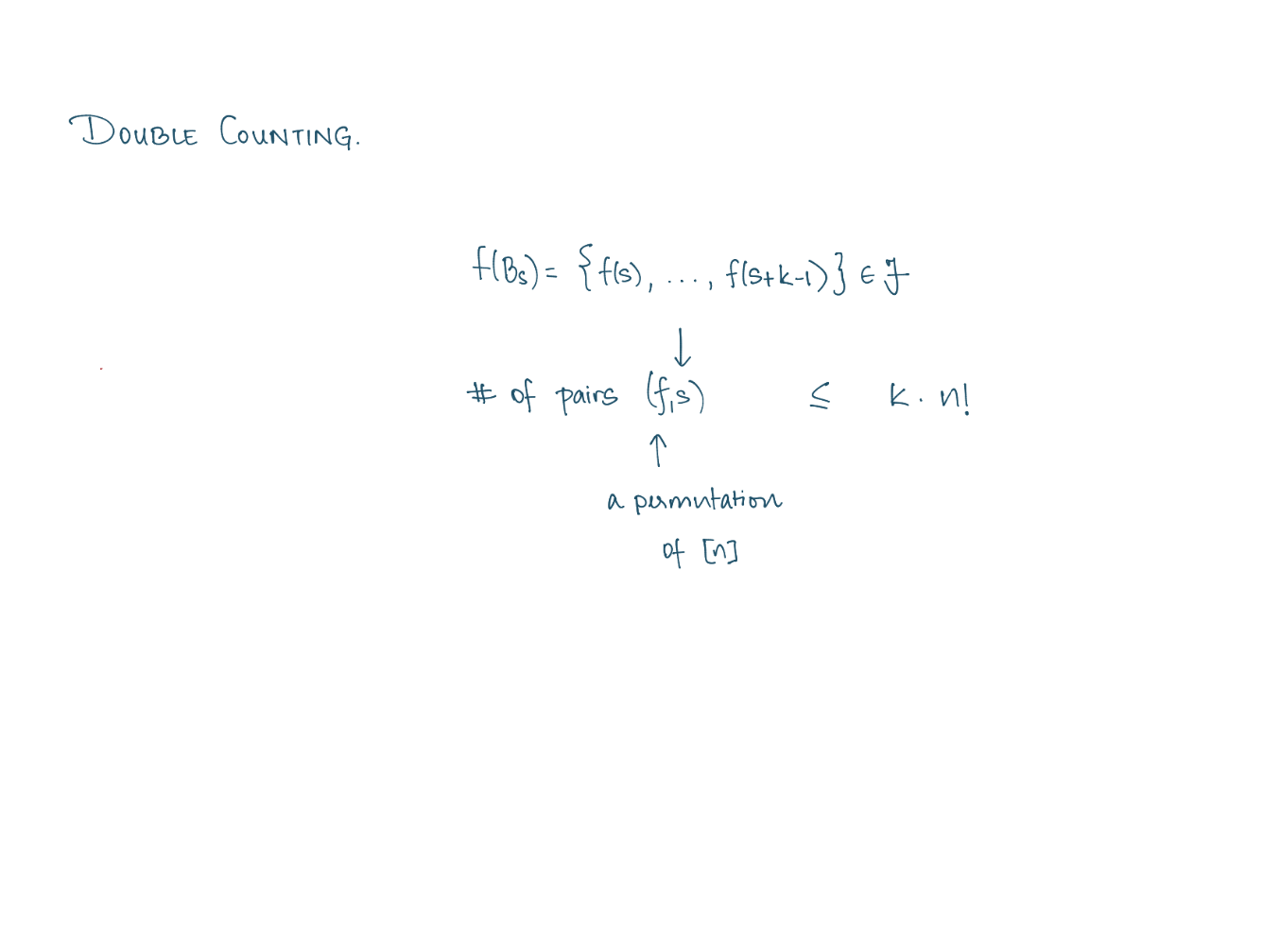
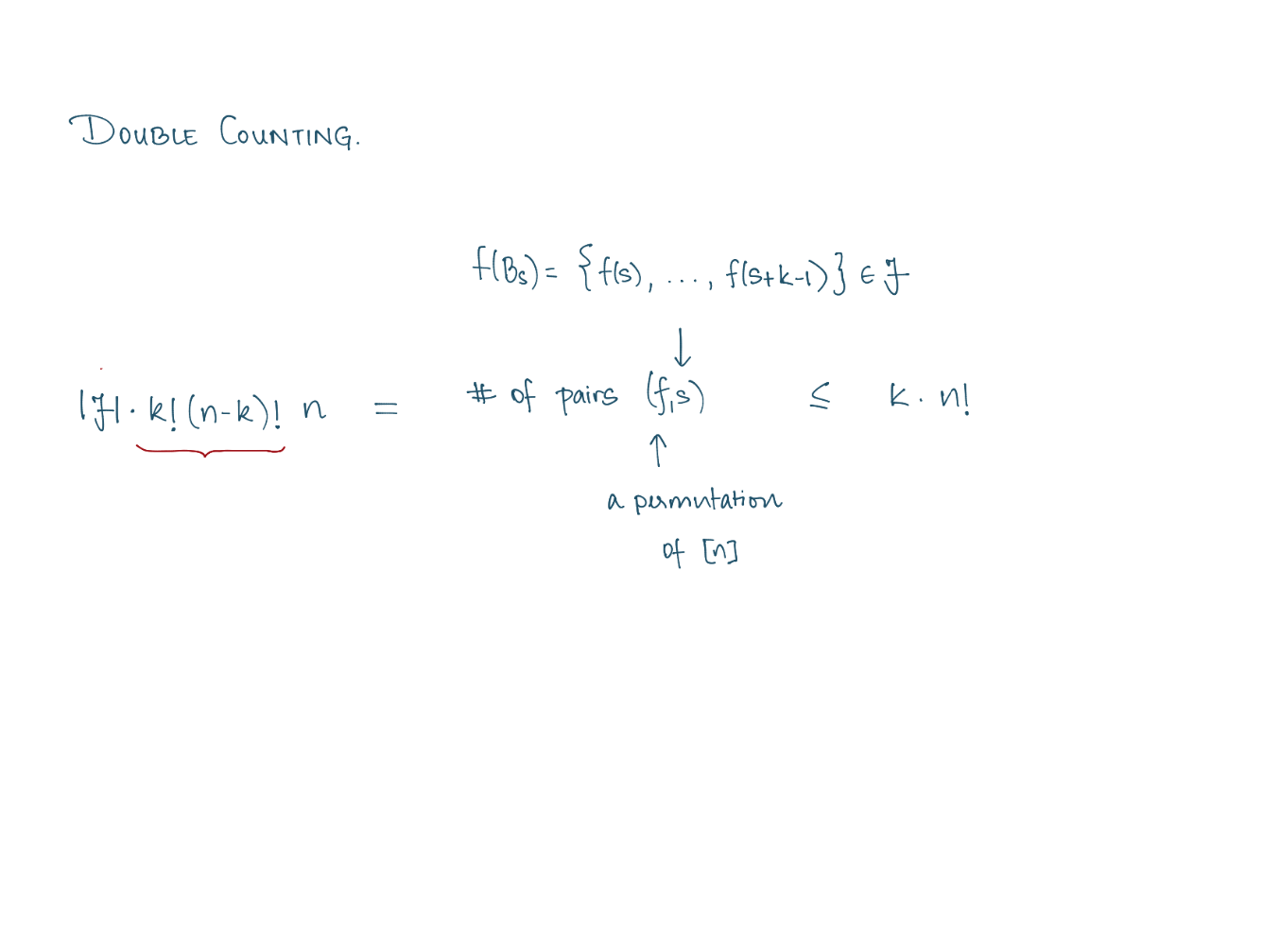
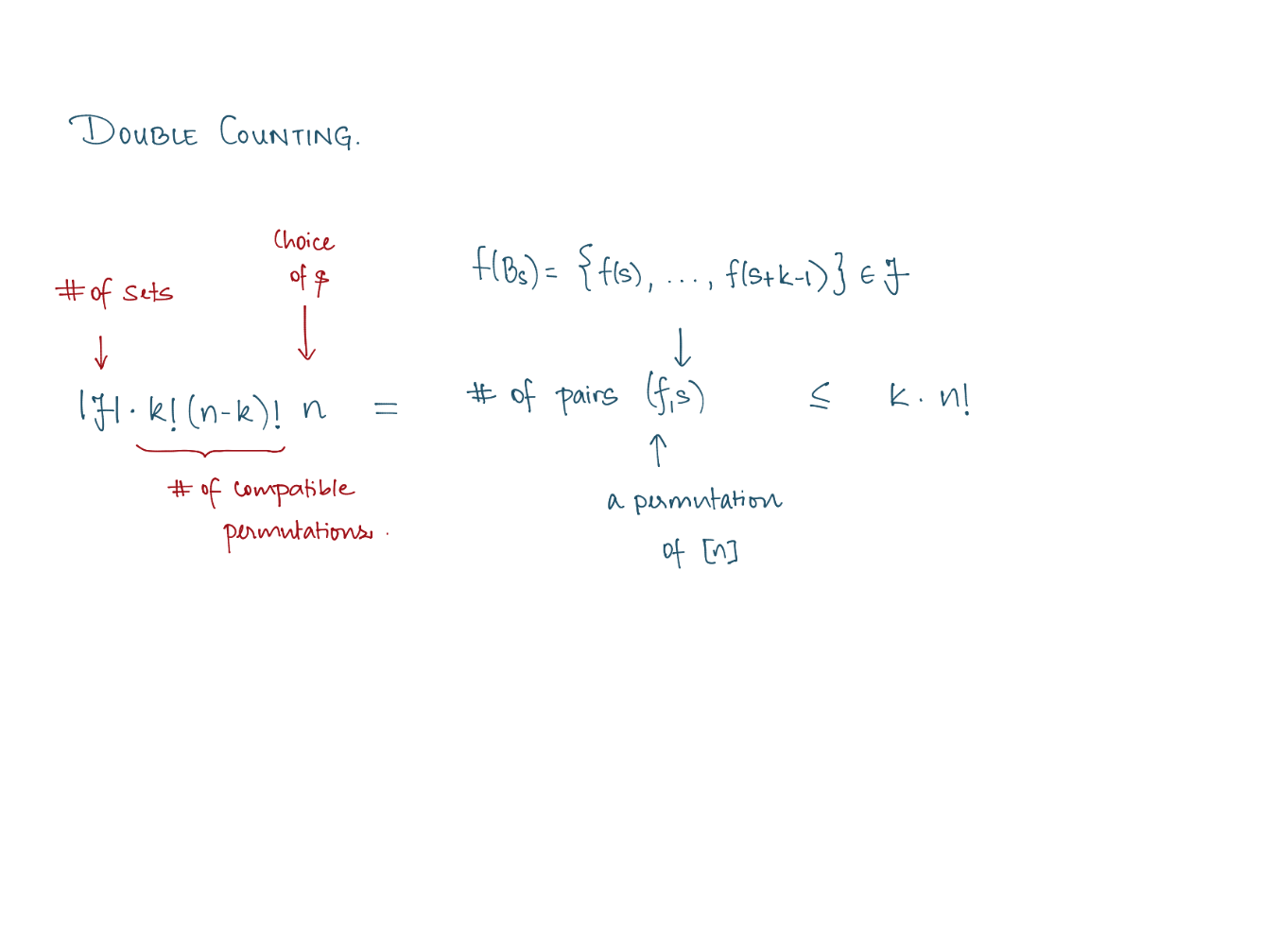
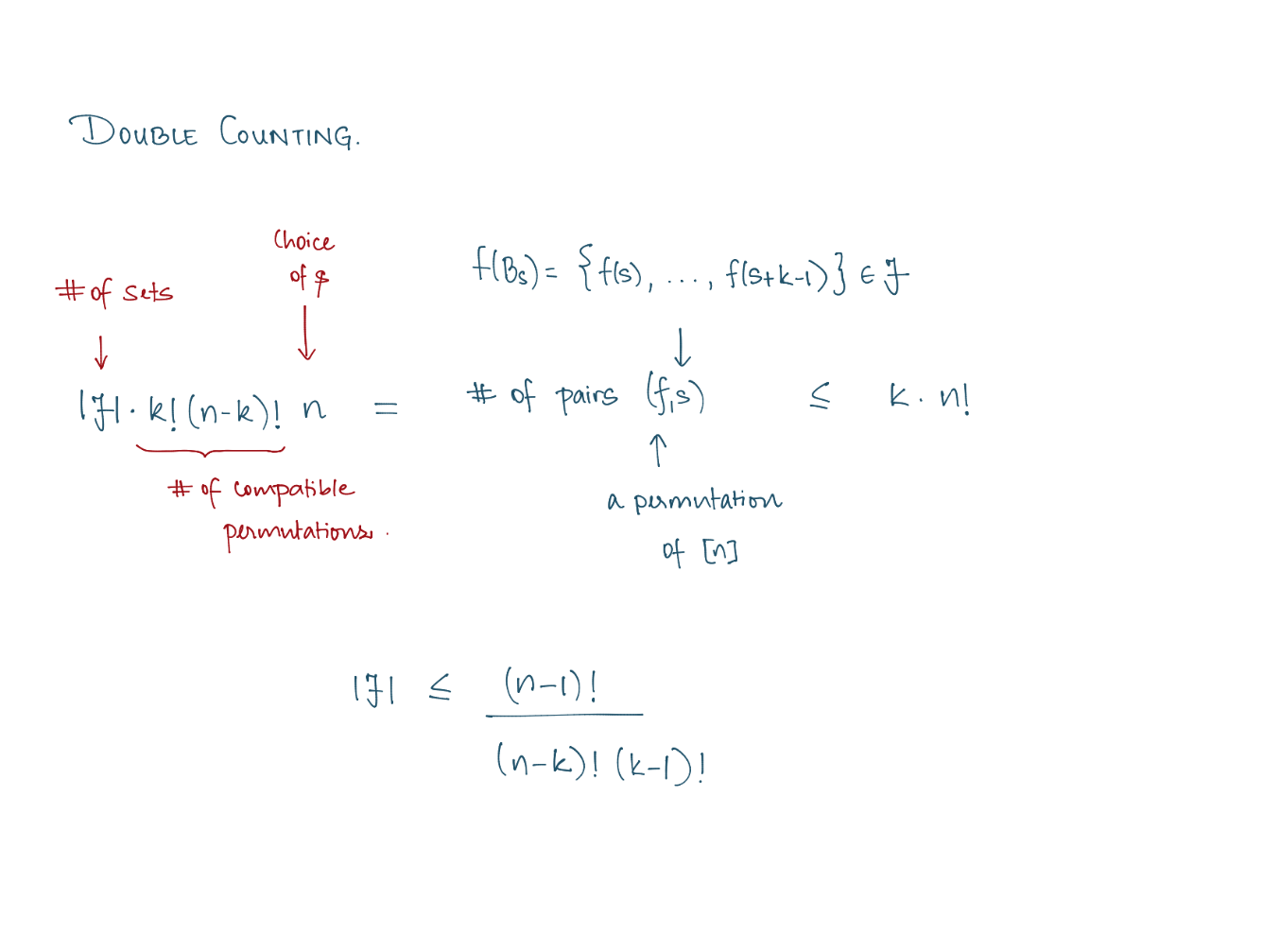
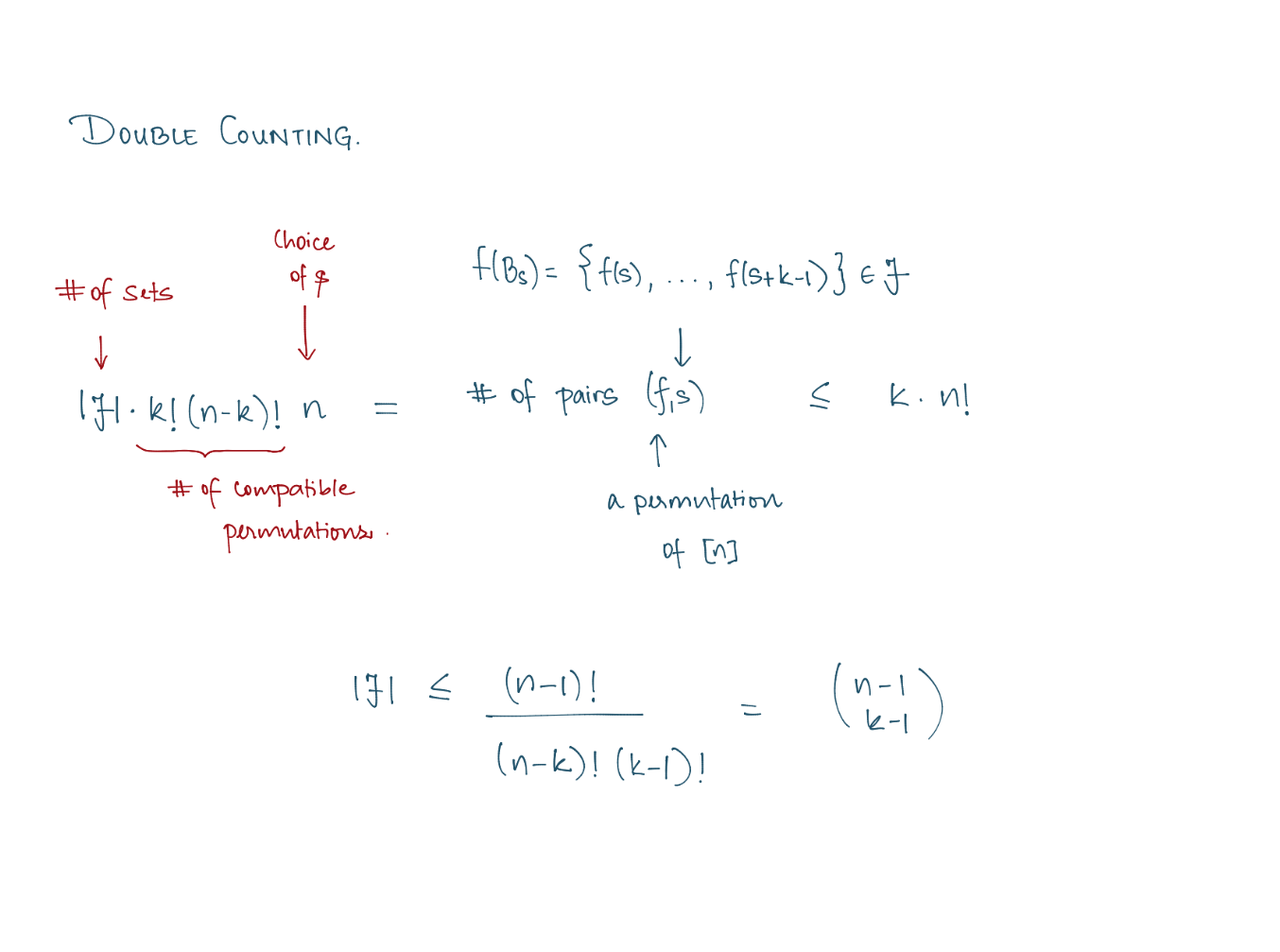
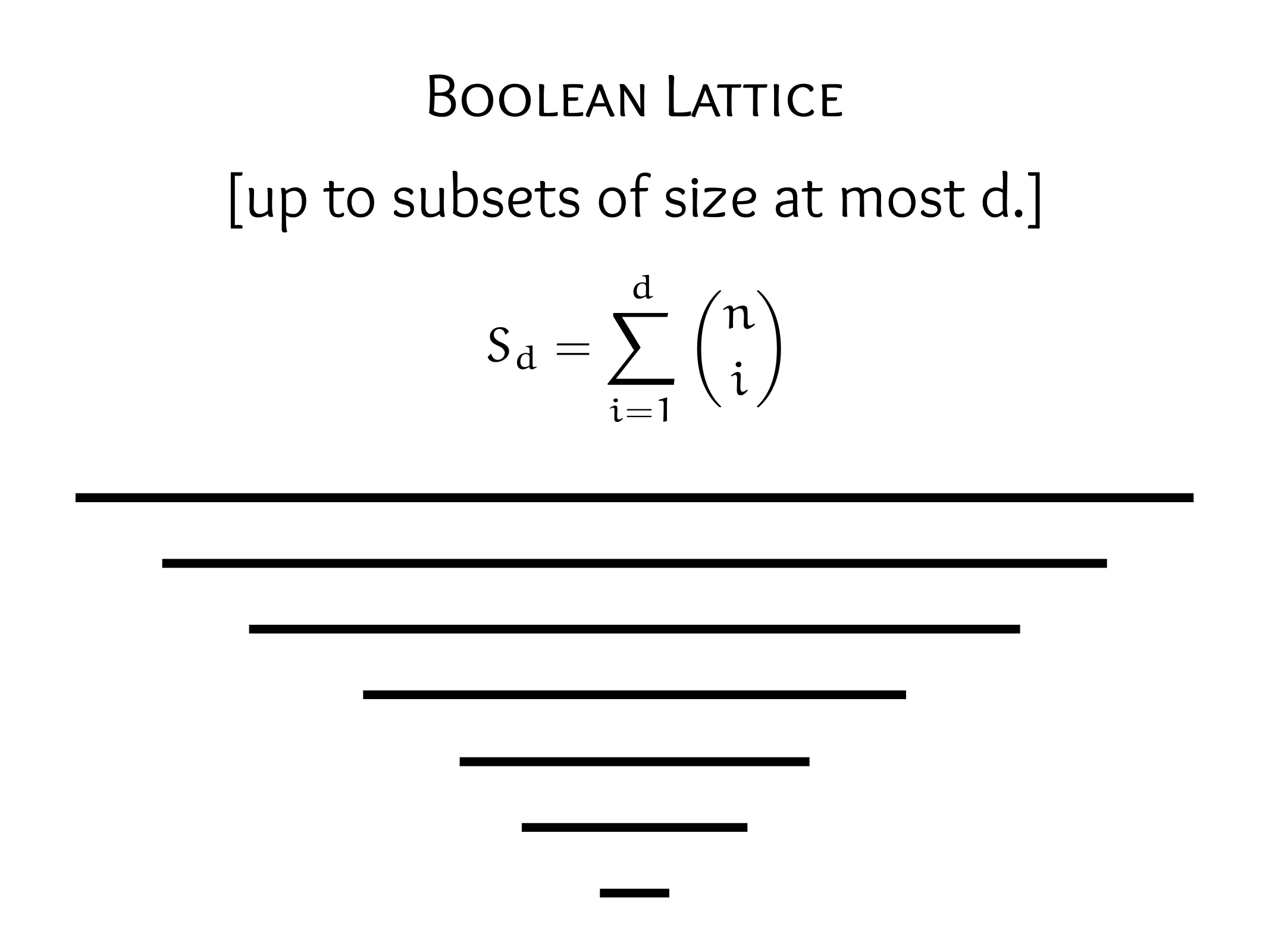
Theorem (E. Sperner, 1927).
Let \(S_1, S_2, \ldots, S_m\) be subsets of an n-element set \(X\) such that \(S_i \nsubseteq S_j\) for \(i \neq j\).
Then \(m \leq\binom{ n}{\lfloor n / 2\rfloor}\), achieved by taking all \(\lfloor n / 2\rfloor\)-element subsets of \(X\).
A poset is a finite set upon which an
ordering relation \(\leqslant\) has been defined.
Note: It is not necessary for any two elements to be related by \(\leqslant\).
Whenever one element of a poset lies immediately above another element, we'll say that the first element covers the second.
In other words, \(y\) covers \(x\) whenever \(x \neq y, x \leqslant y\)
and there is no \(z\) distinct from \(x\) and \(y\) with \(x \leqslant z \leqslant y\).
A poset \(P\) which can be split up into \(r+1\) subsets
\(P_0, P_1, P_2, \ldots, P_{r-1}, P_r\)
such that elements in \(P_k\) cover only elements in \(P_{k-1}\) is called graded.
Let \(P=P_0 \cup P_1 \cup \cdots \cup P_n\)
be a finite graded poset of rank \(n\).
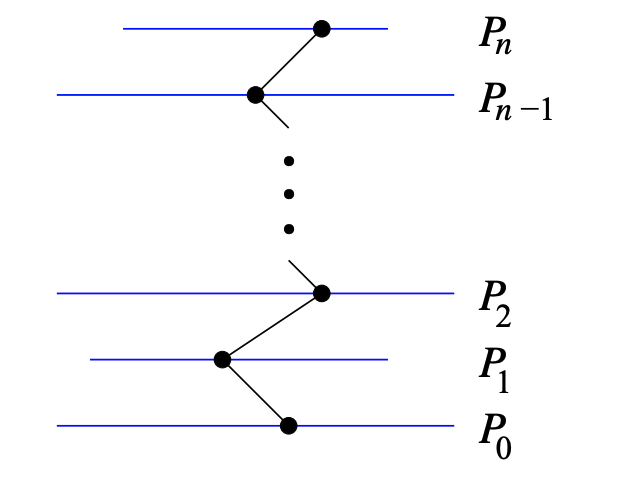
Let \(\boldsymbol{p}_{\boldsymbol{i}}=\# P_i\).
Rank-generating function: \(F_P(q)=\sum_{i=0}^n p_i q^i\)
Rank-symmetric: \(p_i=p_{n-i} \quad \forall i\)
Rank-unimodal: \(p_0 \leq p_1 \leq \cdots \leq p_j \geq p_{j+1} \geq \cdots \geq p_n\) for some \(j\)
rank-unimodal and rank-symmetric \(\Rightarrow j=\lfloor n / 2\rfloor\)
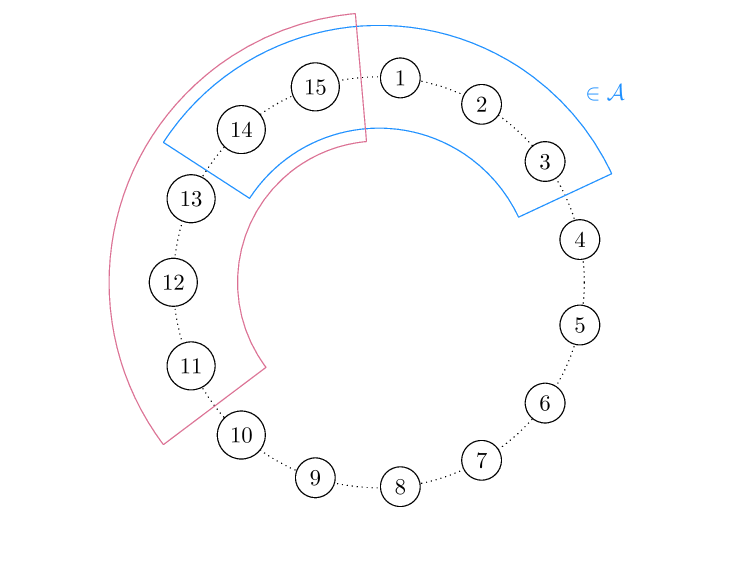
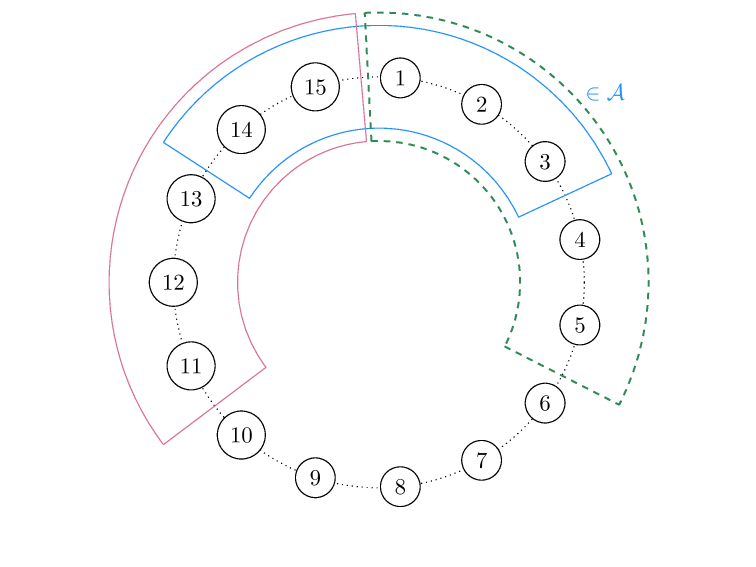
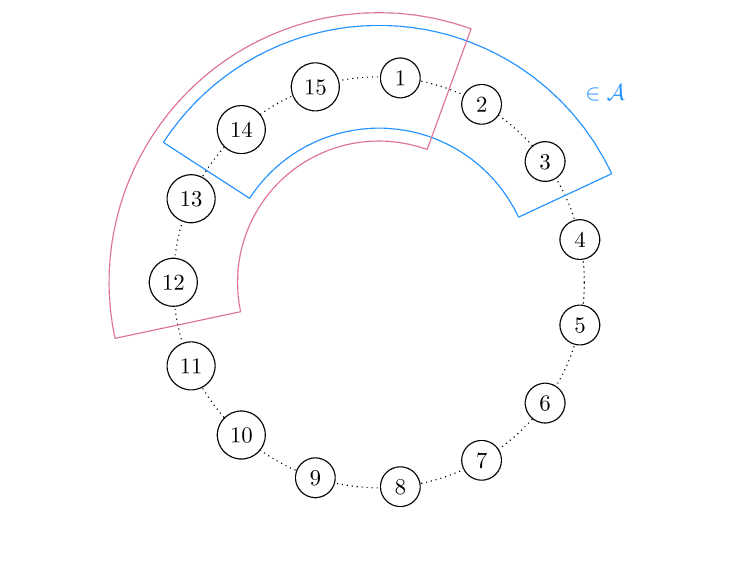
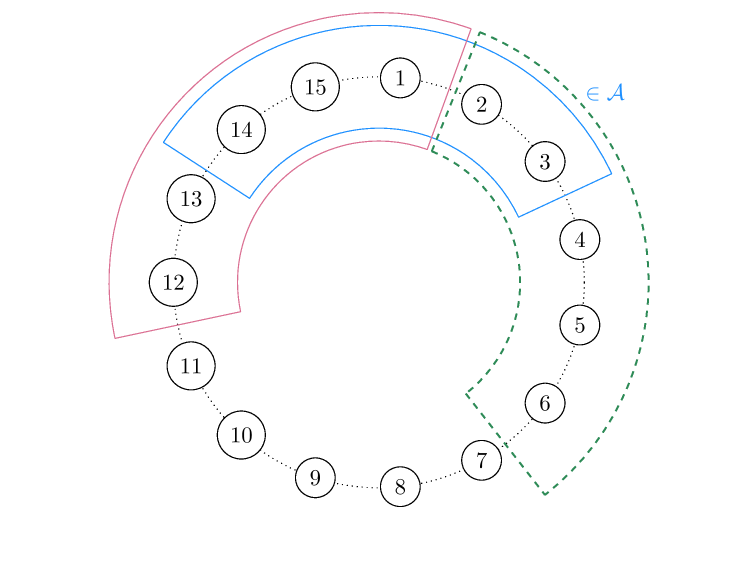
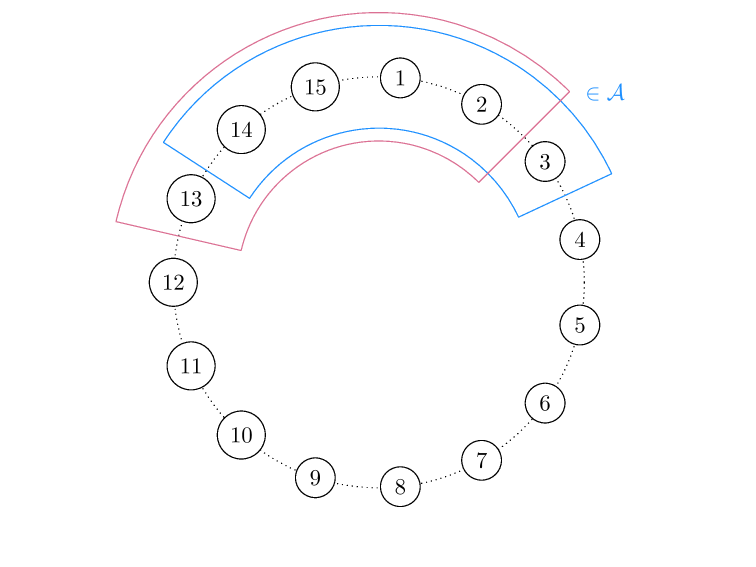
antichain \(A \subseteq P\) :
\(s, t \in A, \quad s \leq t \Rightarrow s=t\)
Note. \(P_i\) is an antichain
\(P\) is Sperner (or has the Sperner property) if
\(\max _A \# A=\max _i p_i\)
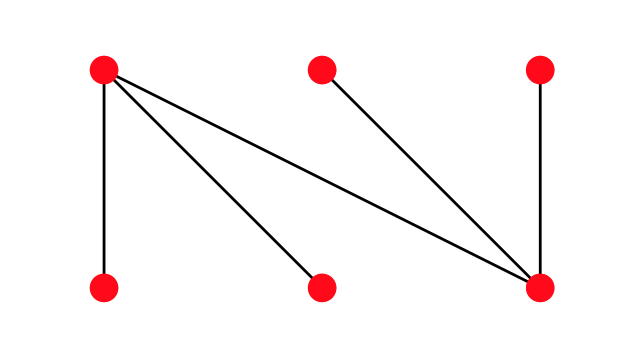
rank-symmetric, rank-unimodal, \(F_P(q)=3+3 q\)

rank-symmetric, rank-unimodal, \(F_P(q)=3+3 q\)
not Sperner!

rank-symmetric, rank-unimodal, \(F_P(q)=3+3 q\)
not Sperner!
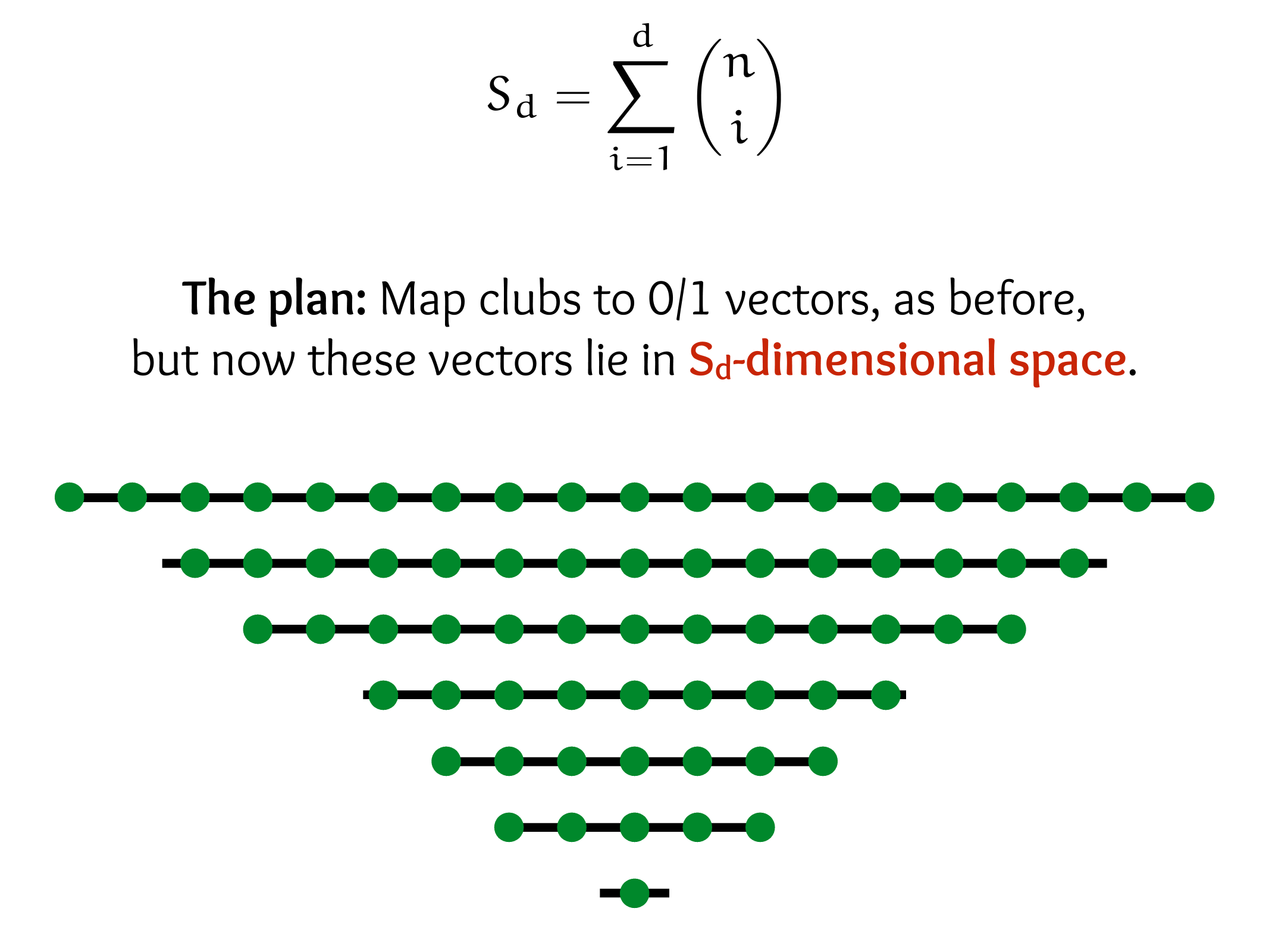
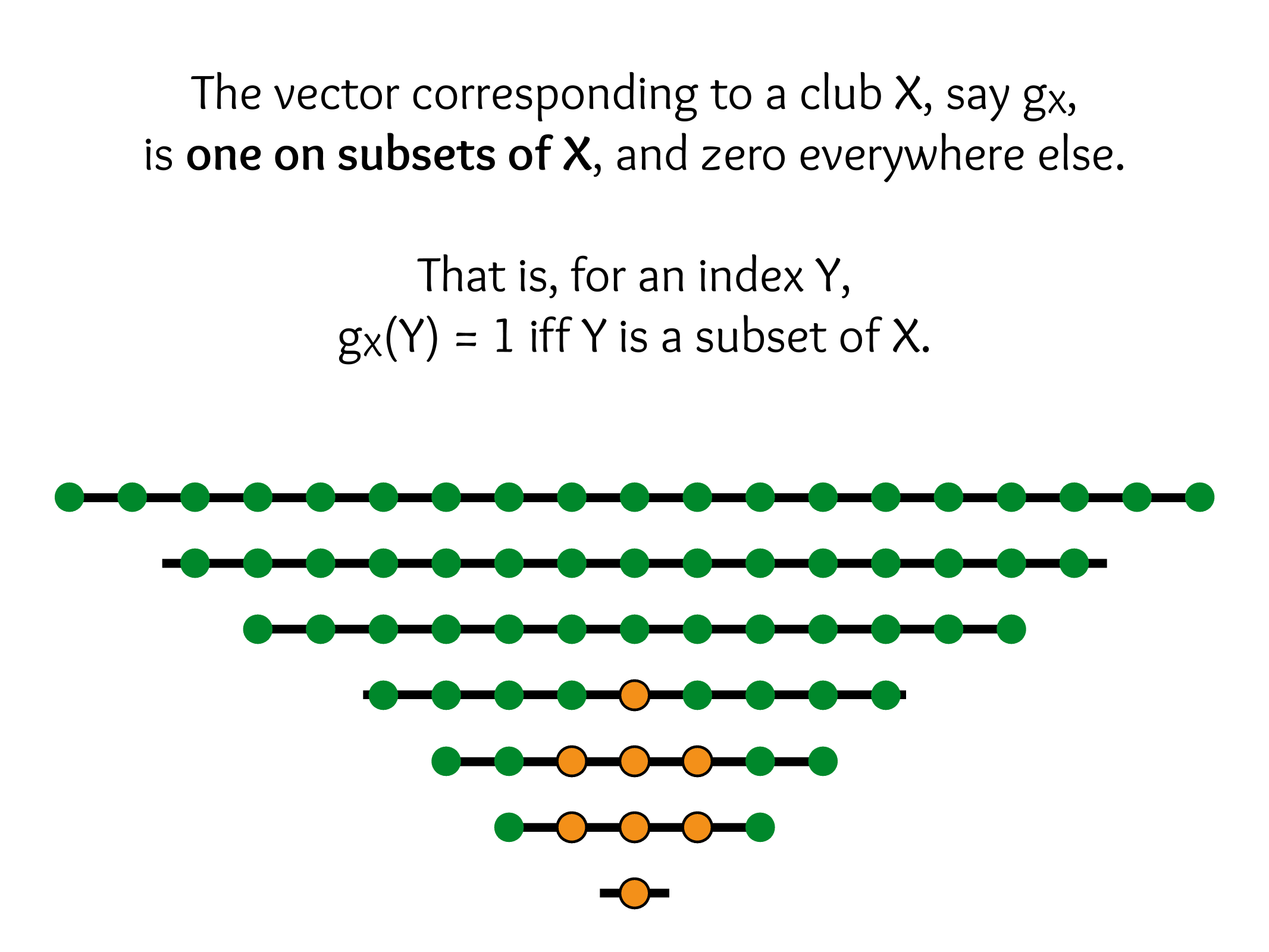
\(B_n\) : subsets of \(\{1,2, \ldots, n\}\), ordered by inclusion
\(p_i=\binom{n}{i}, \quad F_{B_n}(q)=(1+q)^n\)
rank-symmetric?
rank-unimodal?
\(B_n\) : subsets of \(\{1,2, \ldots, n\}\), ordered by inclusion
\(p_i=\binom{n}{i}, \quad F_{B_n}(q)=(1+q)^n\)
rank-symmetric
rank-unimodal
\(B_n\) : subsets of \(\{1,2, \ldots, n\}\), ordered by inclusion
\(p_i=\binom{n}{i}, \quad F_{B_n}(q)=(1+q)^n\)
rank-symmetric
rank-unimodal
Theorem. The boolean algebra \(B_n\) is Sperner.
\(B_n\) : subsets of \(\{1,2, \ldots, n\}\), ordered by inclusion
Theorem. The boolean algebra \(B_n\) is Sperner.
(Lubell's proof.)
\(B_n\) : subsets of \(\{1,2, \ldots, n\}\), ordered by inclusion
Theorem. The boolean algebra \(B_n\) is Sperner.
(Lubell's proof.)
Lubell's proof carries over to all
graded posets \(P\) of rank \(n\) satisfying:
(a) The number of elements covered by \(x \in P\) depends only on \(\operatorname{rank}(x)\).
(b) The number of elements covering \(x \in P\) depends only on \(\operatorname{rank}(x)\).
\(\mu: P_i \rightarrow P_{i+1}\) : injective and \(\mu(t)>t\)
\(\mu: P_i \rightarrow P_{i-1}\) : injective and \(\mu(t)<t\)


\(P_i\)
\(P_{i+1}\)
\(P_{i-1}\)
\(P_{i}\)
Order Matching
Theorem. Let \(P\) be graded of rank \(n\).
Suppose that for some \(j\) there exist order-matchings
\(P_0 \rightarrow P_1 \rightarrow \cdots \rightarrow P_j \leftarrow P_{j+1} \leftarrow \cdots \leftarrow P_n.\)
Then \(P\) is rank-unimodal and Sperner.







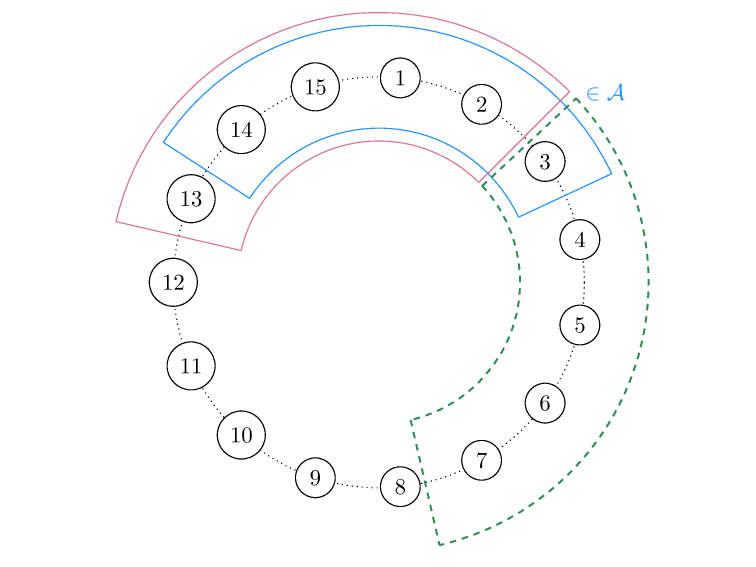
\(\begin{gathered}P=C_1 \cup \cdots \cup C_{p_j} \quad(\text { chains }) \\A=\text { antichain, } C=\text { chain } \Rightarrow \#(A \cap C) \leq 1 \\\Rightarrow \# A \leq p_j .\end{gathered}\)
\(\begin{gathered}P=C_1 \cup \cdots \cup C_{p_j} \quad(\text { chains }) \\A=\text { antichain, } C=\text { chain } \Rightarrow \#(A \cap C) \leq 1 \\\Rightarrow \# A \leq p_j .\end{gathered}\)
For any finite set \(S\), let \(\mathbb{R} S\) denote the real vector space consisting of all formal linear combinations
(with real coefficients)
of elements of \(S\).
Thus, \(S\) is a basis for it.
Lemma. Suppose there are linear transformations \(U: \mathbb{R} P_i \rightarrow \mathbb{R} P_{i+1}\)
satisfying:
- \(U\) is one-to-one, and
- for all \(x \in P_i, U(x)\) is a linear combination of elements \(y \in P_{i+1}\) with \(x<y\)
(we say that \(U\) is an order raising operator).
Then, there exists an order-matching \(f: P_i \rightarrow P_{i+1}\).
Lemma. Suppose there are linear transformations \(U: \mathbb{R} P_i \rightarrow \mathbb{R} P_{i+1}\)
satisfying:
- \(U\) is onto, and
- for all \(x \in P_i, U(x)\) is a linear combination of elements \(y \in P_{i+1}\) with \(x<y\)
(we say that \(U\) is an order raising operator).
Then, there exists an order-matching \(f: P_{i+1} \rightarrow P_i\).
Suppose \(U: \mathbb{R} P_i \rightarrow \mathbb{R} P_{i+1}\) is a one-to-one order raising operator.
Let \([U]\) denote the matrix representing \(U\) with respect to the bases \(P_i\) of \(\mathbb{R} P_i\) and \(P_{i+1}\) of \(\mathbb{R} P_{i+1}\).
Thus, the rows are indexed by the elements
\(\left\{y_i\right\}=P_{i+1}\) and the columns by \(\left\{x_j\right\}=P_i\).
Since \(U\) is one-to-one we have \(\operatorname{rank}[U]=p_i\) and
therefore there are \(p_i\) linearly independent rows.
By relabeling if necessary, we may assume that the first \(p_i\)
(out of \(p_{i+1}\) ) rows are independent.
Let \(A\) be the \(p_i \times p_i\) submatrix consisting of these rows.
Since the rows of \(A\) are linearly independent, we have
\(\operatorname{det}(A)=\sum_{\pi \in S_{p_i}} \operatorname{sign}(\pi) a_{1 \pi(1)} \ldots a_{p_i \pi\left(p_i\right)} \neq 0.\)
Therefore, we can pick a \(\pi \in S_{p_i}\) with \(a_{1 \pi(1)} \ldots a_{p_i \pi\left(p_i\right)} \neq 0\), and observe that since \(U\) is an order-raising operator, we have that \(y_k>x_{\pi(k)}\) for all \(k\).
Indeed, consider \(e_{\pi(k)}\) (the coordinates vector representing \(x_{\pi(k)}\) in the corresponding basis), \(U e_{\pi(k)}\) has a \(y_k\) term in one of its coordinates.
Hence, the map \(f: P_i \rightarrow P_{i+1}\) defined by \(f\left(x_k\right)=y_{\pi^{-1}(k)}\) is an ordered matching as desired.
Goal. Apply this to the Boolean lattice
to derive that it has the Sperner property.
In other words, come up with a linear transformation
\(U_i: \mathbb{R}\left(B_n\right)_i \rightarrow \mathbb{R}\left(B_n\right)_{i+1}\) for all \(0 \leq i<n\),
and then prove it has the desired properties.
We can define \(U_i\) in the most natural way as:
\(U_i(x)=\sum_{y \in\left(B_n\right)_{i+1}, y>x} y\)
Exercise. Show that this actually works.























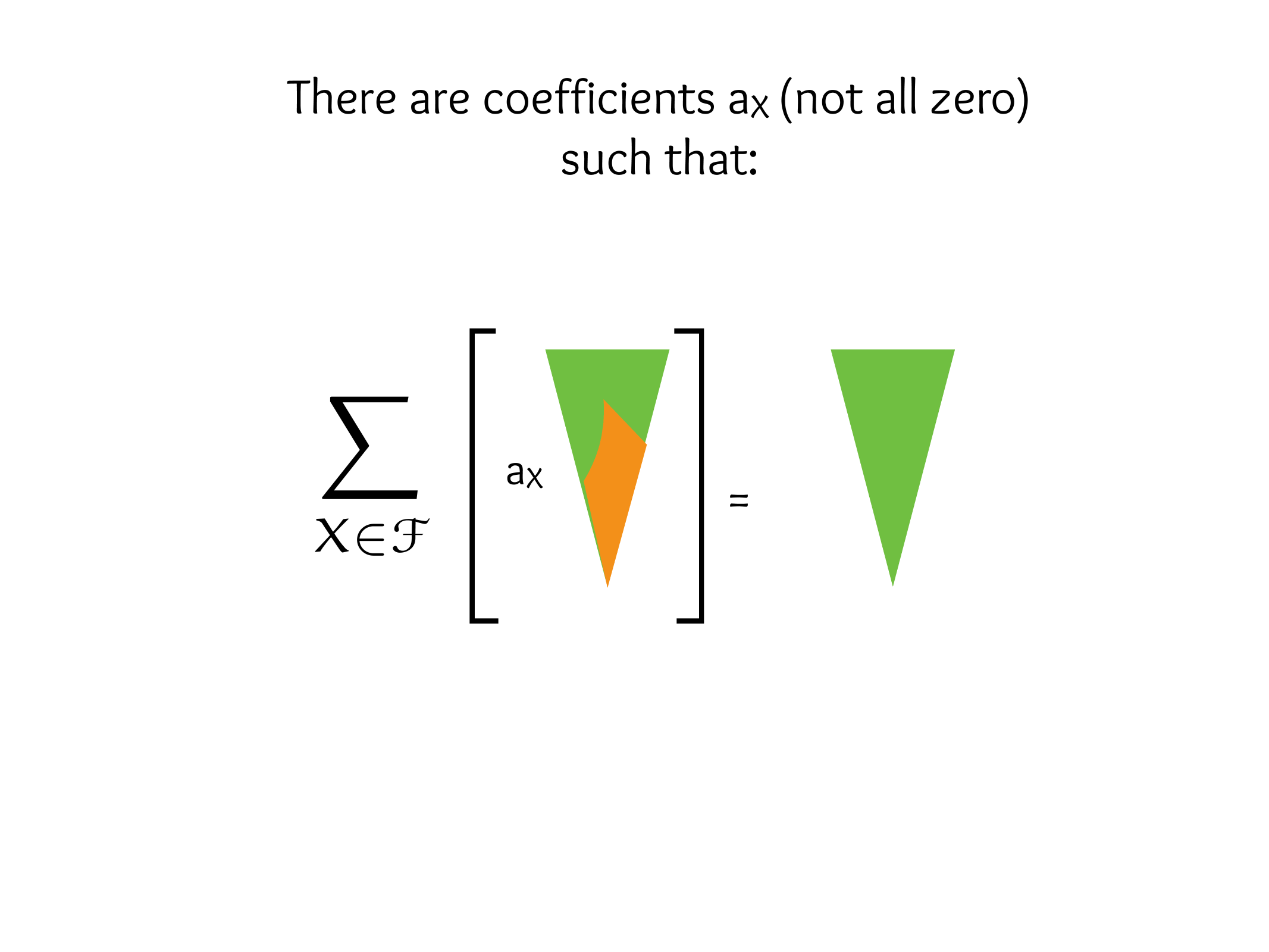
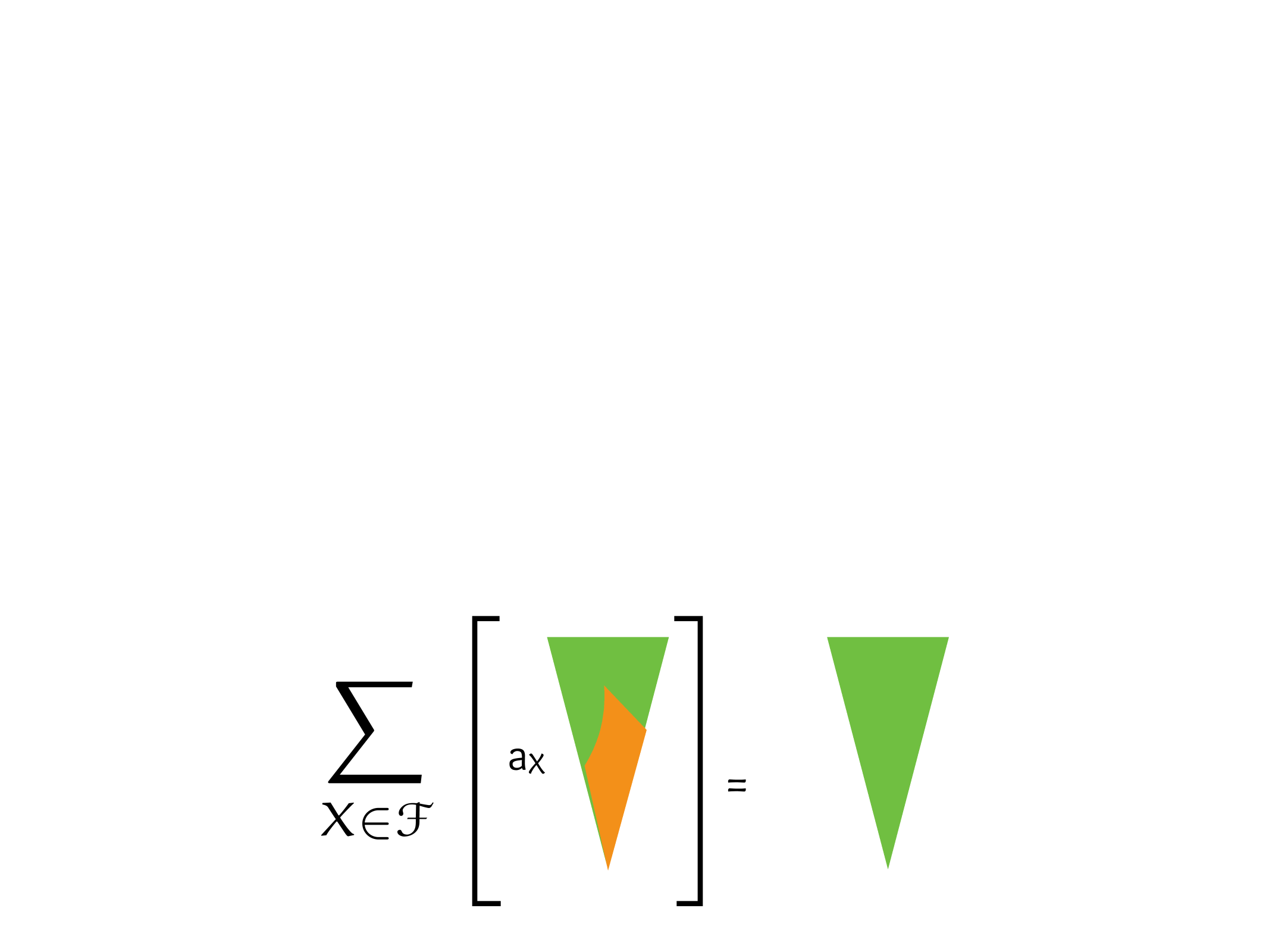
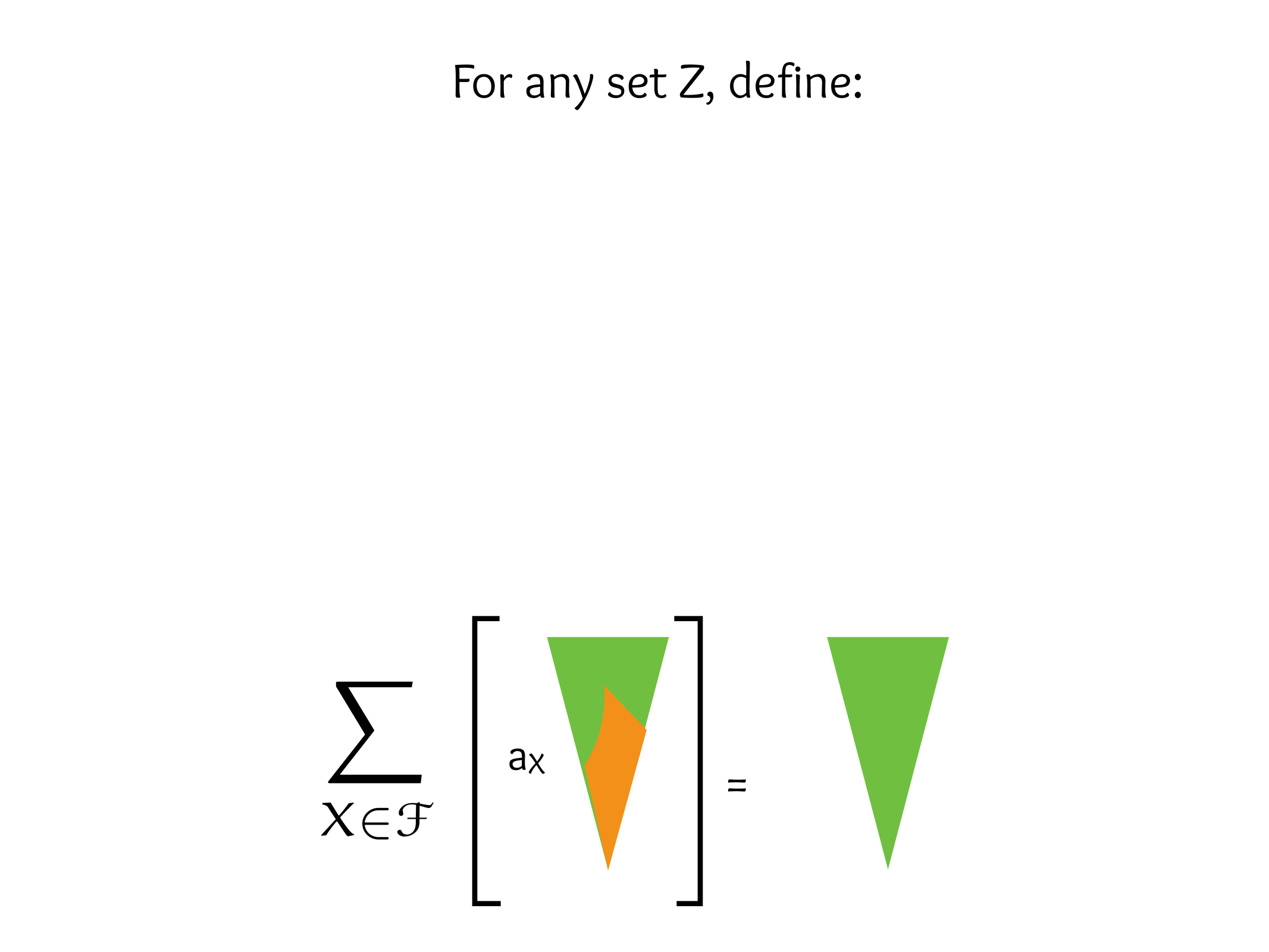
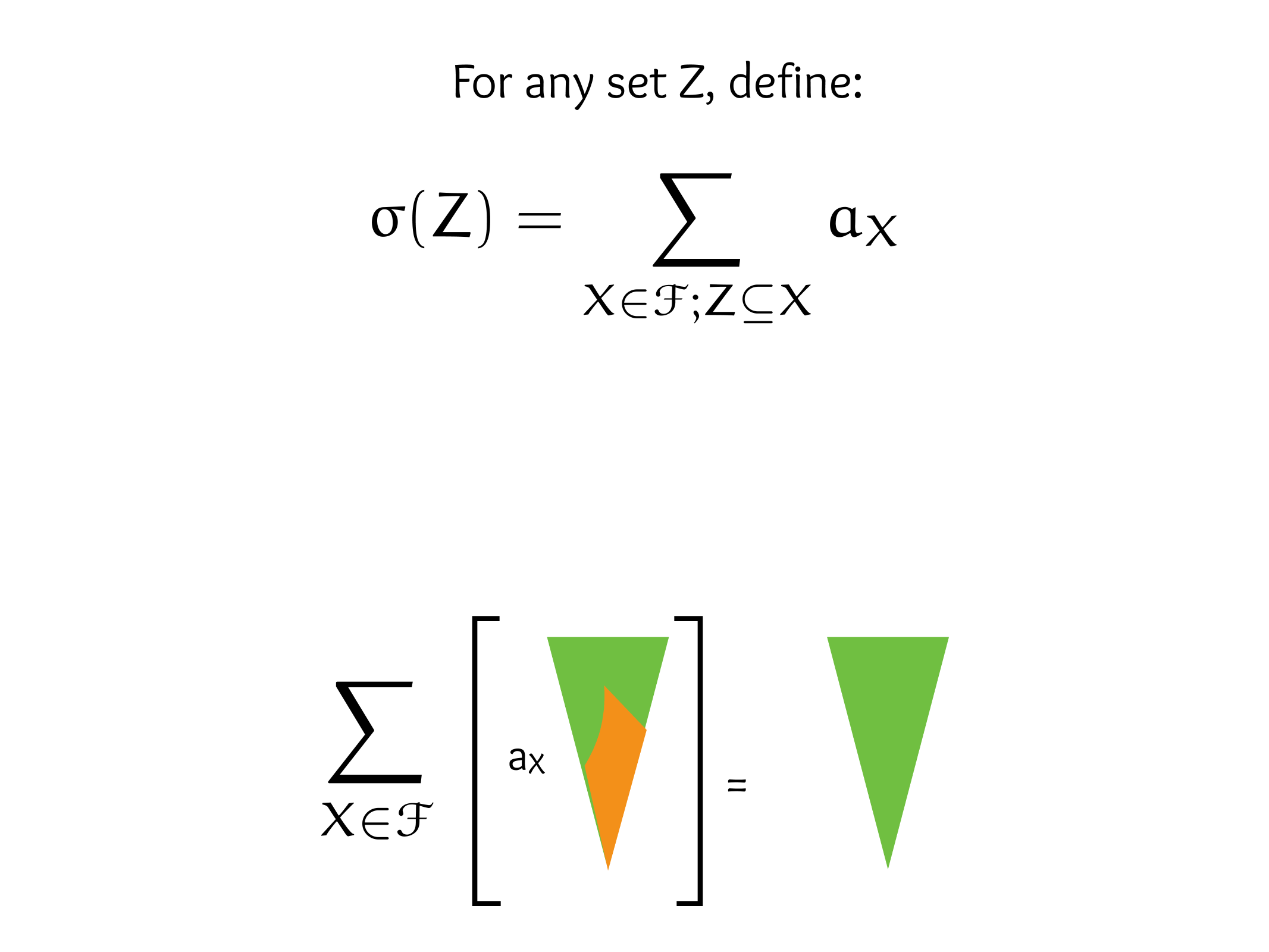


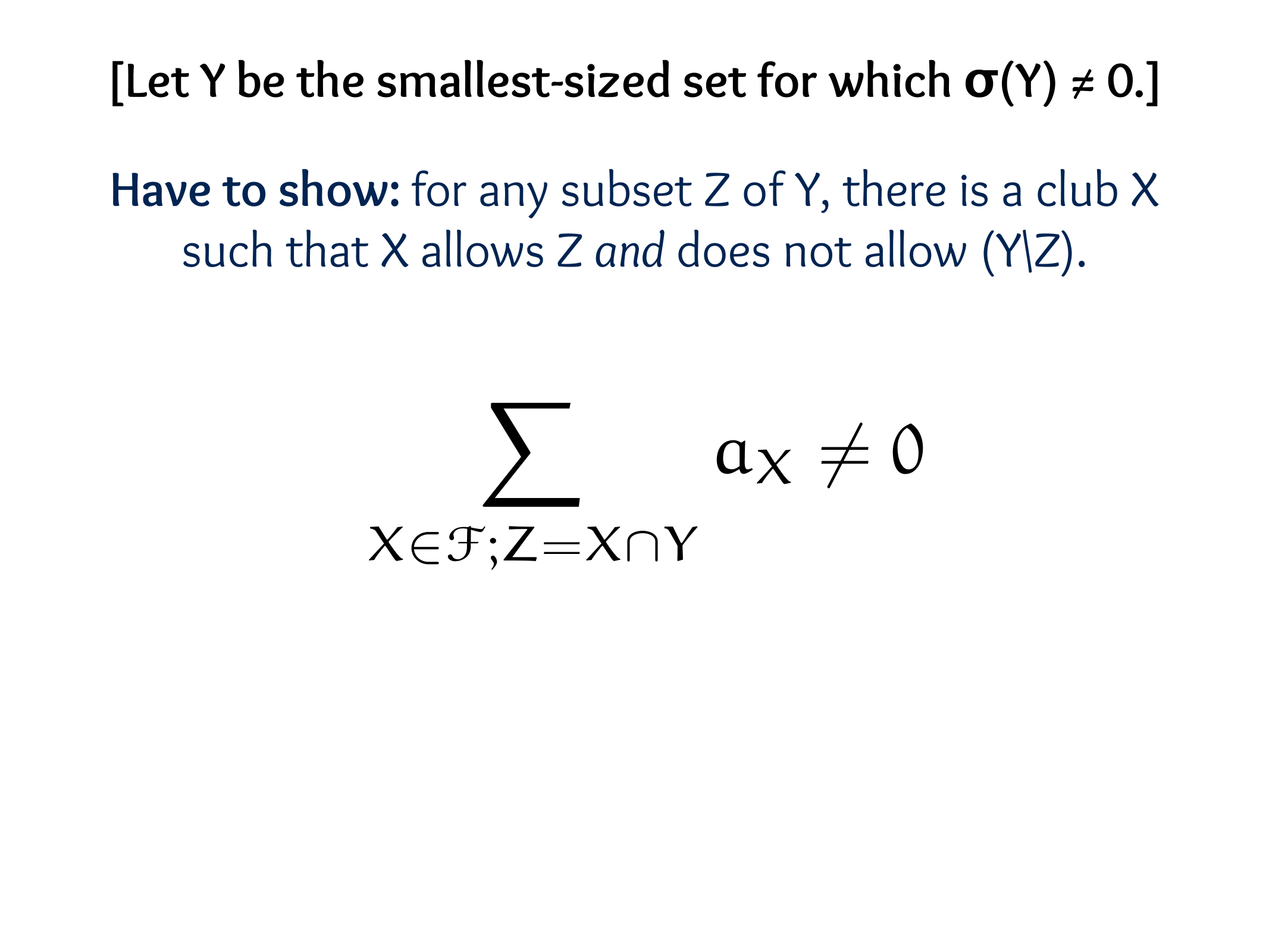


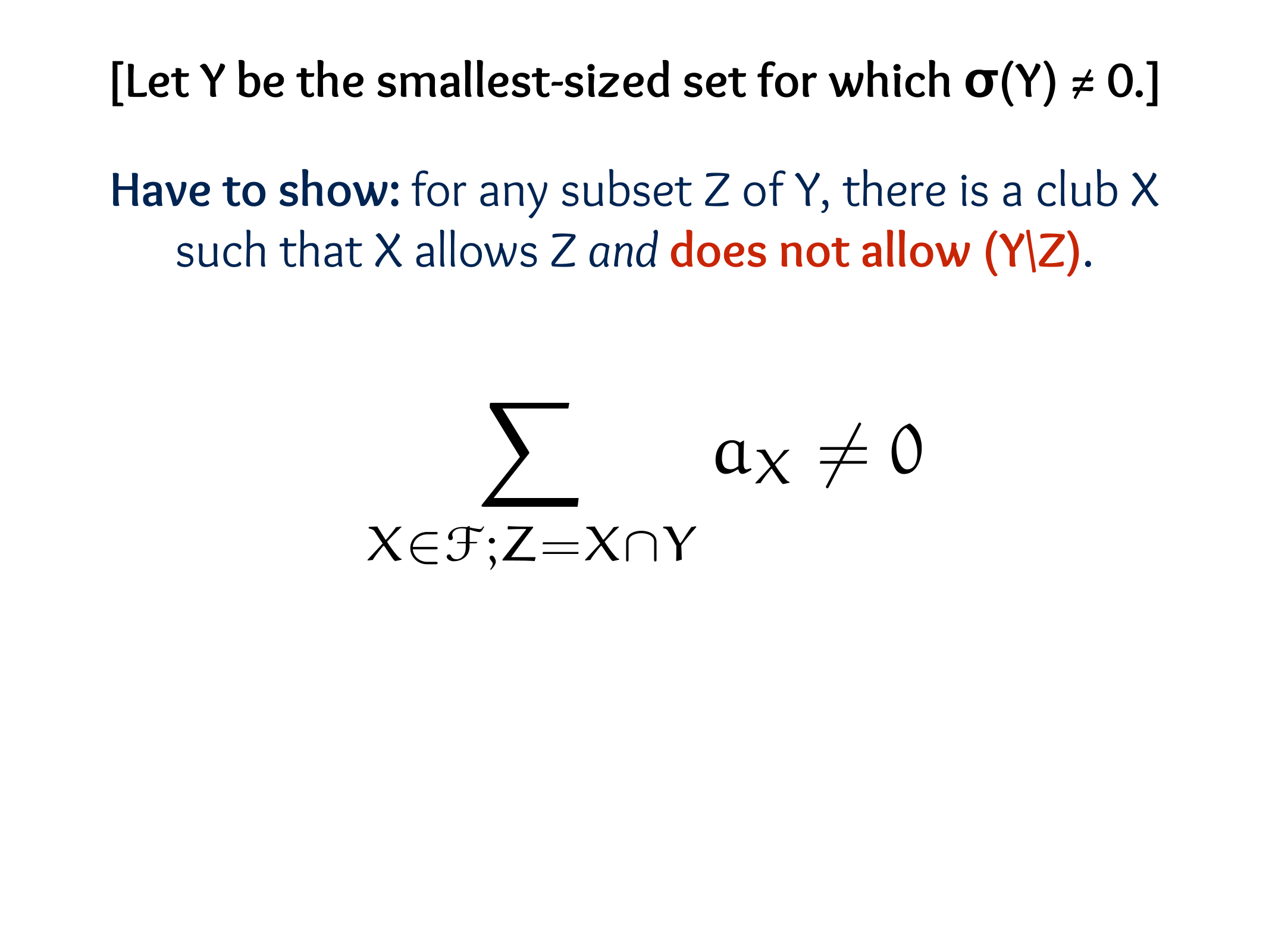









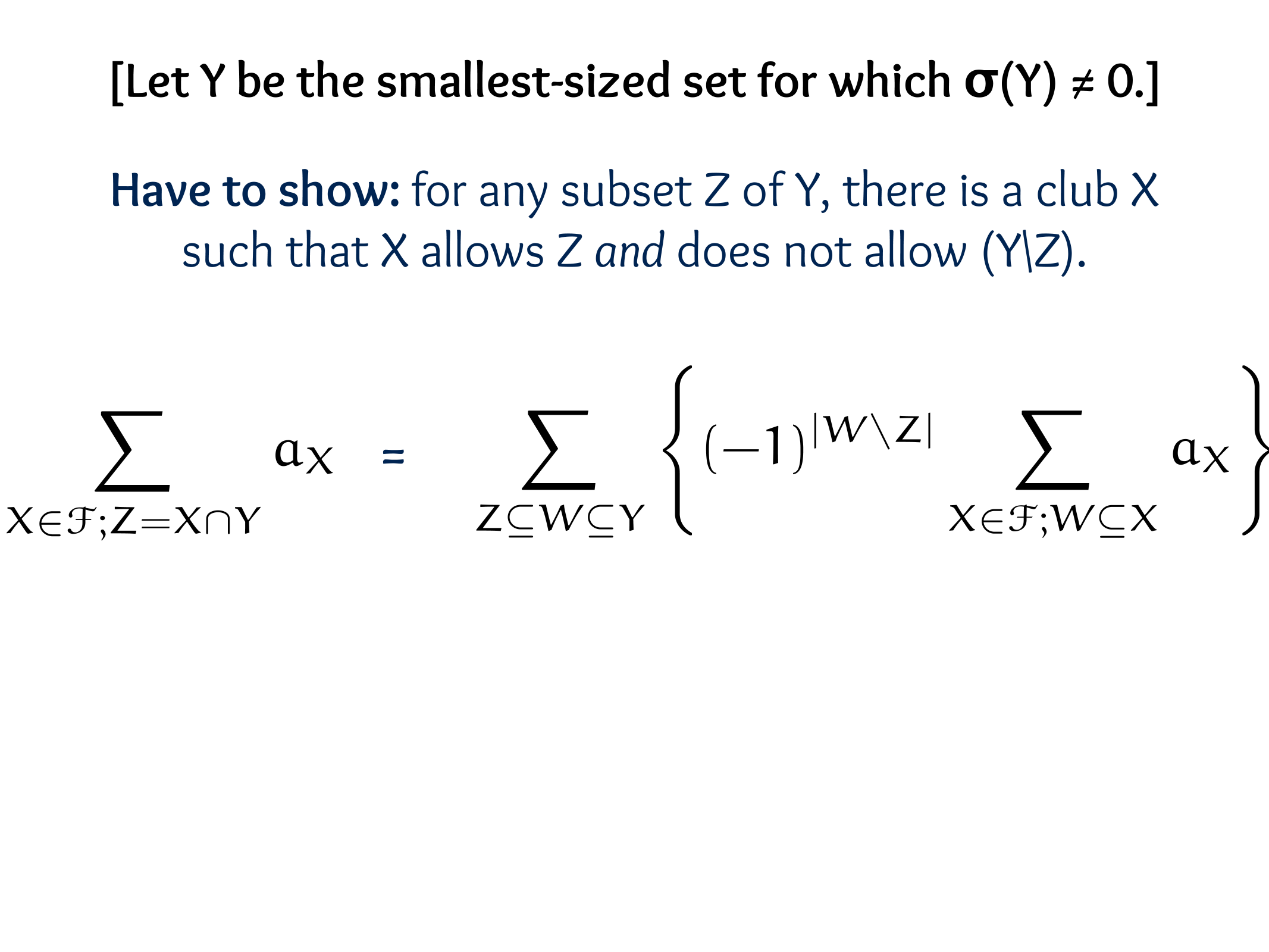
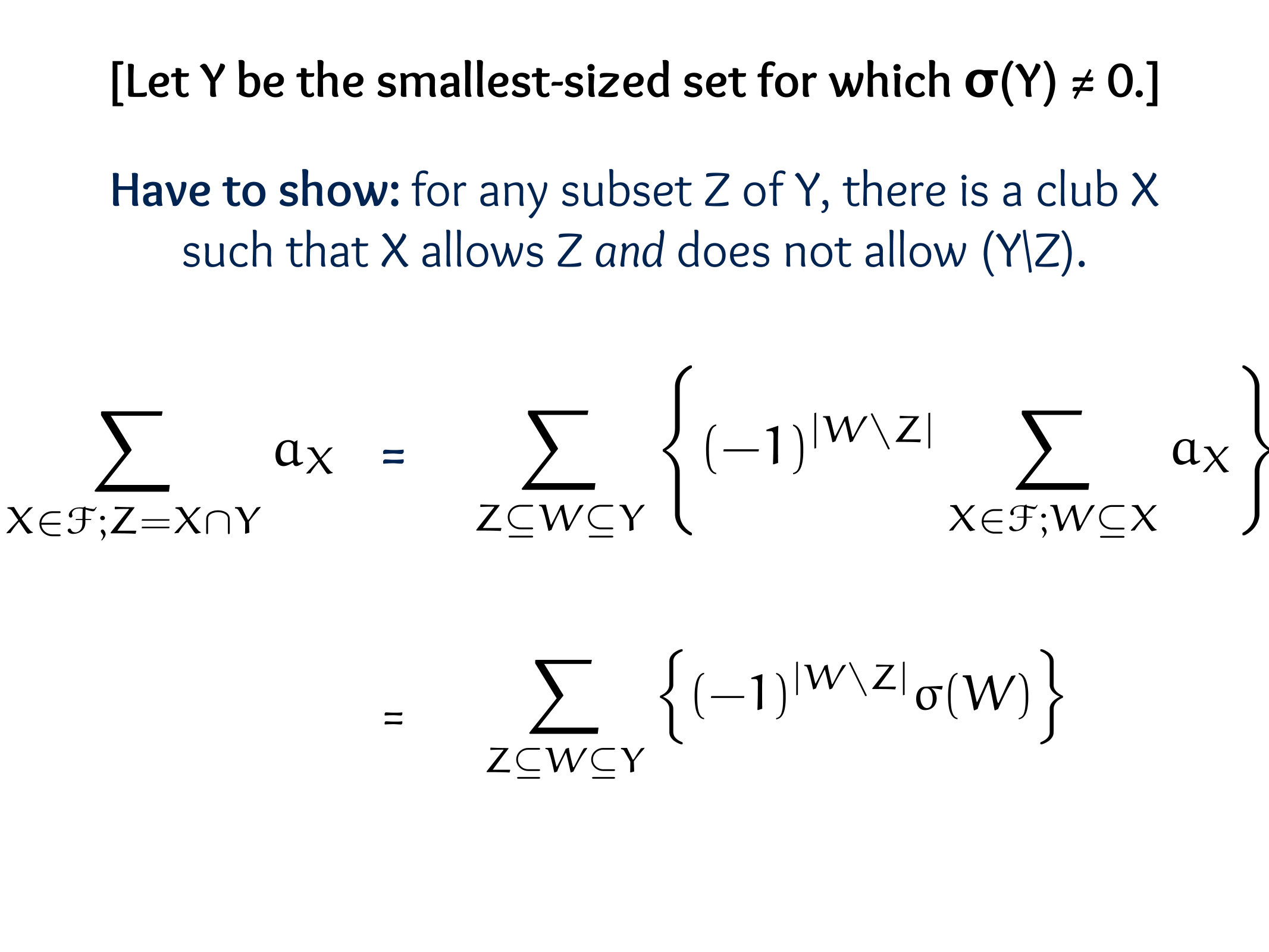
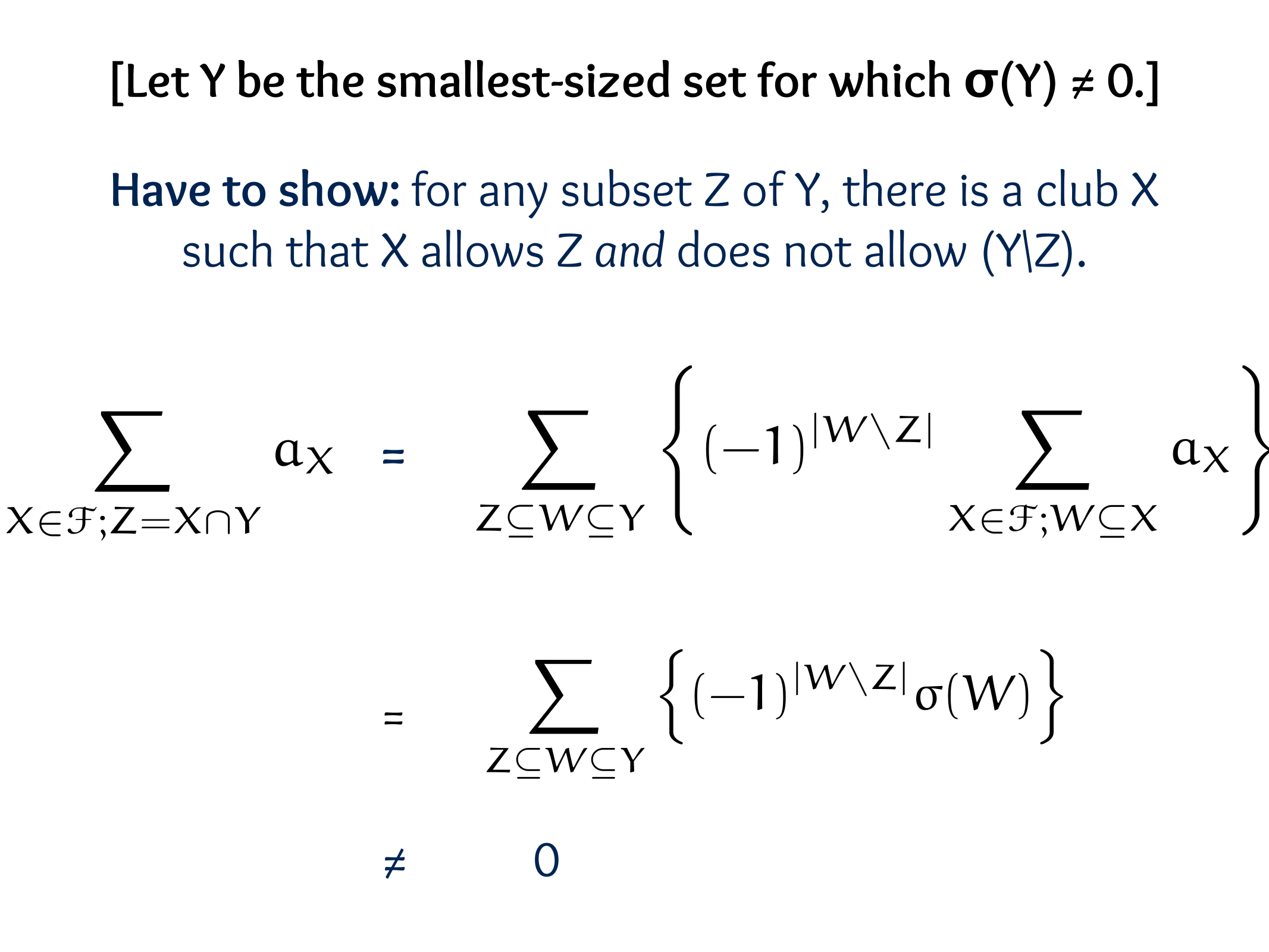







EKR, Sperner, Saur-Shelah
By Neeldhara Misra
EKR, Sperner, Saur-Shelah
- 1,275



