Discrete mathematics
Slides ⋅ Week 01 ⋅ 2nd and 3rd August, 2023
Grading Policy
- Each of the three exams account for 20% of the grade.
- Each of the eleven tutorials will have a quiz worth 5 points. The total number of points you can earn through quizzes is capped at 40, and accounts for 40% of the grade.
- There will be weekly assignments that are not graded but are recommended for practice.
TAs
- Harshil Mittal (mittal_harshil@iitgn.ac.in)
- Saraswati Nanoti (nanoti_saraswati@iitgn.ac.in)
- Eshwar Dhande (eshwar.dhande@iitgn.ac.in)
Office hours
- ADH details will be announced shortly
- OH with instructors by appointment
Google classroom
For announcements, we will use Google Classroom. Please sign up here or use the code nzl3hkr.
Course website
Mathmatize
For in-class quizzes, we will use Mathmatize. All quizzes are open-notes, closed-internet, and solo efforts unless otherwise mentioned.
Sign up here: https://mathmatize.com/c/809
Materials for the course are available from this slide deck
and the course website, which you can access from here.
Reach 100 Game
Player 1 starts with a number between 1 and 10 (inclusive).
Players take turns to add X to the current number, where X is between 1 and 10 (inclusive).
The first person to reach 100 wins.
Let's play!
The Game of SET
The Game of SET
How many sets are there?
How many completions are there for two cards?
How many completions are there for one card?
Can you create a collection of 12 cards with no set in it?
Can you create a collection of 21 cards with no set in it?
How many cards are there?

The Mutilated Chessboard Puzzle
another tiling puzzle


Two players take turns coloring any uncolored lines.
One player colors in one color, and the other colors in another color.
Each player trying to avoid
the creation of a triangle made solely of their color.
(Only triangles with the dots as all corners count;
intersections of lines are not relevant.)
The player who completes such a triangle loses immediately.
The pigeon-hole principle
The pigeonhole principle states that if n items are put into m containers, with n > m, then at least one container must contain more than one item.
Deceptively simple - crazy wide-ranging applications! :)
A chess tournament has N participants, and any two players play one game against each other.
Then it is true that in any given point of time, there are two players who have finished the same number of games?
Discrete mathematics
Slides ⋅ Week 02 ⋅ 8th and 9th August, 2023
SETS
“A set is a gathering together into a whole of definite, distinct objects of our perception or of our thought—which are called elements of the set.”
– Georg Cantor
SETS
A set is an arbitrary collection of objects, absolutely no restriction being placed on the nature and number of these objects, the elements of the set in question.
The elements constitute and determine the set as such, without any ordering or relationship of any kind between them.
von Neumann and Morgenstern
before 1901:
Most sets commonly encountered are not members of themselves.
For example, consider the set of all students in ES214.
This set is not a student, much less one enrolled in ES214, thus it is not a member of itself.
Let us call a set normal if it is not a member of itself,
& abnormal if it is a member of itself.
Clearly every set must be either normal or abnormal.
The set of all students enrolled in ES214 is a normal set.
In contrast, the complementary set that contains everything that is not a student enrolled in ES214 is not a student enrolled in ES214,
& so it is one of its own members and is therefore abnormal.
russel's paradox - informal
Now we consider the set of all normal sets, R, and try to determine whether R is normal or abnormal.
russel's paradox - informal
If R were normal, it would be contained in the set of all normal sets (itself), and therefore be abnormal.
If R were abnormal, it would not be contained in the set of all normal sets (itself), and therefore be normal.
This leads to the conclusion that R is neither normal nor abnormal: Russell's paradox.
(formulation borrowed from Wikipedia)
naive set theory
A set is an unordered collection of distinct objects, called elements or members of the set.
A set is said to contain its elements.
We write a ∈ A to denote that a is an element of the set A.
The notation a ∉ A denotes that a is not an element of the set A.
A set is an unordered collection of distinct objects, called elements or members of the set.
A set is said to contain its elements.
We write a ∈ A to denote that a is an element of the set A.
The notation a ∉ A denotes that a is not an element of the set A.
Ops: union, intersection, difference, symmetric difference
naive set theory
How do we represent sets in a computer?
What do we care about?
Check for membership
Updates (addition, deletion)
SETS in memory
Find out more in DSA :)
Want: Efficiency in time & space
PIE
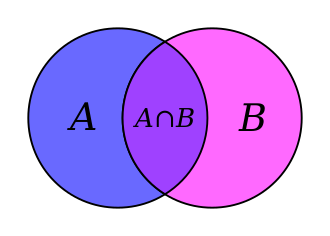
A. There are 72 students enrolled in ES214.
B. There are 145 students enrolled in ES242.
The intersection is 59. What is the union?
PIE
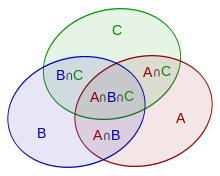
\(S(A \cup B \cup C)=\)
\(S(A)+S(B)+S(C)\)
\(-S(A \cap B)-S(A \cap C)-S(B \cap C)\)
\(+S(A \cap B \cap C)\)
To compute the size of a union of multiple sets, it is necessary to
sum the sizes of these sets separately,
and then subtract the sizes of all pairwise intersections of the sets,
then add back the size of the intersections of triples of the sets,
subtract the size of quadruples of the sets,
and so on, up to the intersection of all sets.
PIE
PIE
The above definition can be expressed mathematically as follows:
\(\left|\bigcup_{i=1}^n A_i\right|=\)
And in a more compact way:
\(\left|\bigcup_{i=1}^n A_i\right|=\sum_{\emptyset \neq J \subseteq\{1,2, \ldots, n\}}(-1)^{|J|-1}\left|\bigcap_{j \in J} A_j\right|\)
\(\sum_{i=1}^n\left|A_i\right|-\sum_{1 \leq i<j \leq n}\left|A_i \cap A_j\right|+\sum_{1 \leq i<j<k \leq n}\left|A_i \cap A_j \cap A_k\right|-\cdots+(-1)^{n-1}\left|A_1 \cap \cdots \cap A_n\right|\)
PIE
\(T=\left(\begin{array}{l}k \\ 1\end{array}\right)-\left(\begin{array}{l}k \\ 2\end{array}\right)+\left(\begin{array}{l}k \\ 3\end{array}\right)-\cdots+(-1)^{i-1} \cdot\left(\begin{array}{l}k \\ i\end{array}\right)+\cdots+(-1)^{k-1} \cdot\left(\begin{array}{l}k \\ k\end{array}\right)\)
\((1-x)^k=\left(\begin{array}{l}k \\ 0\end{array}\right)-\left(\begin{array}{l}k \\ 1\end{array}\right) \cdot x+\left(\begin{array}{l}k \\ 2\end{array}\right) \cdot x^2-\left(\begin{array}{l}k \\ 3\end{array}\right) \cdot x^3+\cdots+(-1)^k \cdot\left(\begin{array}{l}k \\ k\end{array}\right) \cdot x^k\)
\(0 = 1 - T \Longrightarrow T = 1\)
T := # of times an element is counted on the RHS
PIE: Applications
Given two numbers n and r,
count the number of integers in the interval [1 ; r]
that are relatively prime to n
(their greatest common divisor is 1 ).
Suppose \(n = p_1^{b_1} \cdot p_2^{b_2} \cdots p_k^{b_k}\).
Let \(A_i\) be the set of numbers between 1 and r that are a multiple of \(p_i\).
Apply PIE on the \(A_i\)'s to get a count of the number of integers in [1;r] that are not relatively prime to n.
PIE: Applications
Consider n patterns of strings of the same length, consisting only of letters \((a \ldots z\)) or question marks.
You're also given a number k.
A string matches a pattern if it has the same length as the pattern, and at each position, either the corresponding characters are equal or the character in the pattern is a question mark.
The task is to count the number of strings that match
exactly k of the patterns.
PIE: Applications
d
m
s
a
s
i
w
u
m
d
m
s
a
f
i
w
u
l
d
m
s
a
?
?
?
w
s
PIE: Applications
d
m
s
a
?
?
?
w
s
Let Z be a subset of patterns.
Easy: count the number of strings that satisfy at least this set of patterns.
d
m
s
a
?
w
?
?
t
Z
d
m
s
a
w
?
?
t
z
Hard: count the number of strings that satisfy exactly this set of patterns.
PIE: Applications
Fix a specific subset X from the set of patterns consisting of k patterns.
Then we have to count the number of strings that satisfy this set of patterns, and only matches it, that is, they don't match any other pattern.
PIE: Applications
Fix a specific subset X from the set of patterns consisting of k patterns.
Then we have to count the number of strings that satisfy this set of patterns, and only matches it, that is, they don't match any other pattern.
Sum on all supersets Y, and either add to the current answer or subtract it from the number of strings:
\(\operatorname{ans}(X)=\sum_{Y \supseteq X}(-1)^{|Y|-k} \cdot f(Y)\)
Where f(Y) is the number of strings that match at least Y.
PIE: Applications
Fix a specific subset X from the set of patterns consisting of k patterns.
Then we have to count the number of strings that satisfy this set of patterns, and only matches it, that is, they don't match any other pattern.
Note: if we sum up on all X, we will get the final answer:
\(\text { ans }=\sum_{X:|X|=k} \operatorname{ans}(X)\)
Food for thought: what is the running time of this procedure? Can you improve it?
Equality
Do two sets A and B have the same size?
A and B have the same size if there is a bijection between them.
Equality
Do two sets A and B have the same size?
A: the set of all natural numbers
B: the set of all even natural numbers
\(f(x) = 2x\)
Equality
Do two sets A and B have the same size?
A: the set of all integers
B: the set of all natural numbers
\(f(x) = 2x \text{ if } x > 0\)
\(f(x) = -2x+1 \text{ if } x \leqslant 0\)
Equality
Do two sets A and B have the same size?
A: the set of all rational numbers
B: the set of all natural numbers
\(f(p/q) = 2^p 5^q, \text{ for } p \geqslant 0, q > 0 \)
\(f(-p/q) = 3^p 5^q, \text{ for } p,q > 0\)
Equality
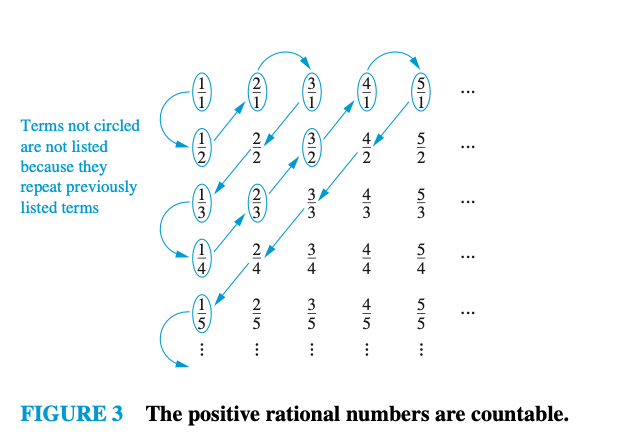
Source: Rosen
Hilbert's Grand Hotel has infinitely many rooms, each a luxurious full-floor suite, numbered like the natural numbers: 0, 1, 2, and so on, endlessly.
Each room has a guest, and the hotel is completely full, with infinitely many guests.
But meanwhile, a new guest has just arrived, wanting a room.
What is the manager to do?
Source: Proof and the Art of Mathematics, J. D. Hamkins
Room n → Room n + 1
hilbert's hotel


Hilbert's Grand Hotel has infinitely many rooms, each a luxurious full-floor suite, numbered like the natural numbers: 0, 1, 2, and so on, endlessly.
Each room has a guest, and the hotel is completely full, with infinitely many guests.
On the weekend, a crowd shows up all at once 1000 guests.
What is the manager to do?
Source: Proof and the Art of Mathematics, J. D. Hamkins
Room n → Room n + 1000
hilbert's hotel

hilbert's hotel

Hilbert's Grand Hotel has infinitely many rooms, each a luxurious full-floor suite, numbered like the natural numbers: 0, 1, 2, and so on, endlessly.
The following week, Hilbert's bus pulls up. The bus has infinitely many seats, and in every seat there is a new guest wanting to check into the hotel.
What is the manager to do?
Source: Proof and the Art of Mathematics, J. D. Hamkins
Room n → Room 2n; Seat s → Room 2s + 1


hilbert's hotel

Hilbert's Grand Hotel has infinitely many rooms, each a luxurious full-floor suite, numbered like the natural numbers: 0, 1, 2, and so on, endlessly.
The following week, Hilbert's train comes. The train has infinitely many train cars, each with infinitely many seats, and every seat is occupied.
What is the manager to do?
Source: Proof and the Art of Mathematics, J. D. Hamkins
Room n → Room 2n; Car c, Seat s → Room \(3^c5^s\)


hilbert's hotel

Hilbert's Grand Hotel has infinitely many rooms, each a luxurious full-floor suite, numbered like the natural numbers: 0, 1, 2, and so on, endlessly.
Source: Proof and the Art of Mathematics, J. D. Hamkins

Next, Cantor's cruise ship pulls into the harbor, with a passenger for every real number. Every ship passenger has a ticket, with a distinct ticket number printed on it, a real number, and every real number arises on some ticket.
What is the manager to do?
Resign.
hilbert's hotel

A diagonalization argument to show that the reals cannot be placed in one-to-one correspondence with the naturals:
Source: Proof and the Art of Mathematics, J. D. Hamkins


A set is countable if
it can be placed in one-to-one correspondence with a set of natural numbers.
The union of two countable sets is countable.
In other words, if A and B are countable sets, so is A U B.
Definition
Theorem
...by the Odd/Even trick;
or interleaving.
We say that sets A and B are equinumerous, written \(A \simeq B\), if they can be placed into one-to-one correspondence with each other.
In other words, \(A \simeq B\) if there is a bijection \(f: A \rightarrow B\), a one-to-one onto function from A to B.
No set X is equinumerous with its power set P(X),
the set of all subsets of X.
Definition
Theorem
Let f be a proposed bijection that maps X to P(X).
Consider: \(A=\{x \in X \mid x \notin f(x)\}\).
We say that sets A and B are equinumerous, written \(A \simeq B\), if they can be placed into one-to-one correspondence with each other.
In other words, \(A \simeq B\) if there is a bijection \(f: A \rightarrow B\), a one-to-one onto function from A to B.
There is a natural partial order* underlying equinumerosity, namely, \(A \lesssim B\) if there is a one-to-one function \(f: A \rightarrow B\), not necessarily onto.
Definition
We say that sets A and B are equinumerous, written \(A \simeq B\), if they can be placed into one-to-one correspondence with each other.
In other words, \(A \simeq B\) if there is a bijection \(f: A \rightarrow B\), a one-to-one onto function from A to B.
There is a natural partial order* underlying equinumerosity, namely, \(A \lesssim B\) if there is a one-to-one function \(f: A \rightarrow B\), not necessarily onto.
Definition
We say that sets A and B are equinumerous, written \(A \simeq B\), if they can be placed into one-to-one correspondence with each other.
In other words, \(A \simeq B\) if there is a bijection \(f: A \rightarrow B\), a one-to-one onto function from A to B.
It is easy to see that \(X \lesssim P(X)\),
since we may map any element \(a \in X\) to its singleton \(a \mapsto\{a\}\), which is a subset of X, and this is an injective function.
Definition
By simply iterating this process, we thereby produce larger and larger sizes of infinity:
\(\mathbb{N}<P(\mathbb{N})<P(P(\mathbb{N}))<P(P(P(\mathbb{N})))<\cdots\)
We say that sets A and B are equinumerous, written \(A \simeq B\), if they can be placed into one-to-one correspondence with each other.
In other words, \(A \simeq B\) if there is a bijection \(f: A \rightarrow B\), a one-to-one onto function from A to B.
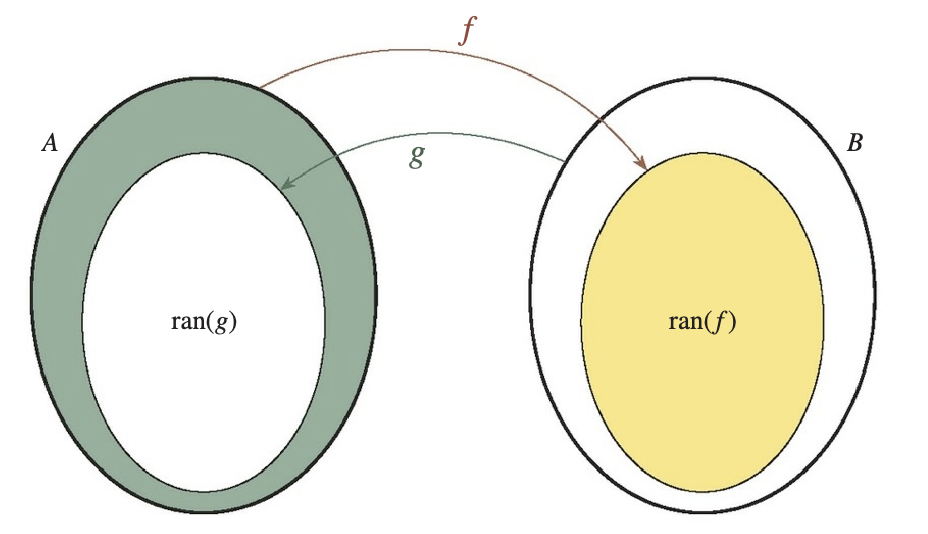
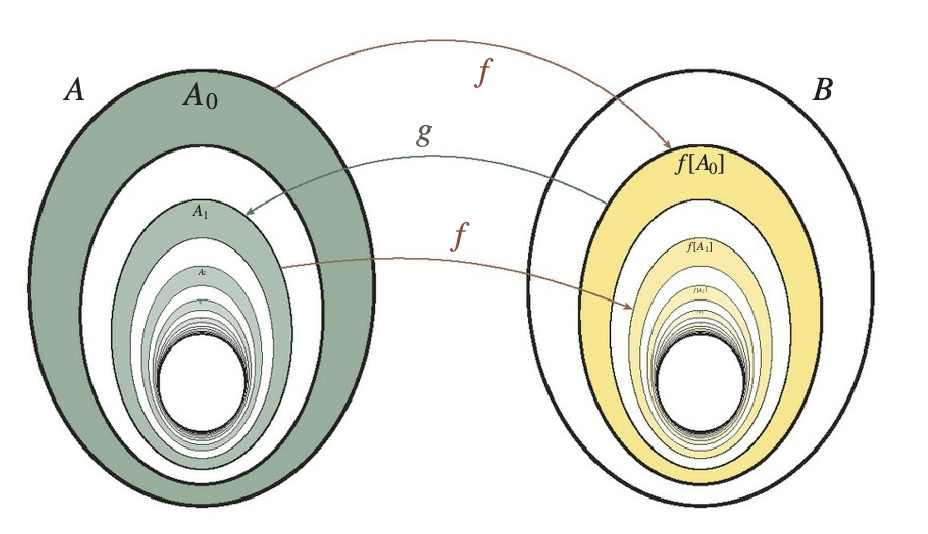
(Shröder-Cantor-Bernstein). If sets A and B are at least as large as each other, then they are equinumerous.
Definition
Theorem
Specifically, if \(A \lesssim B\) and \(B \lesssim A\), then \(A \simeq B\).
In other words, if there is an injective function \(f: A \rightarrow B\) and another injective function \(g: B \rightarrow A\), then there is a bijective function \(h: A \rightarrow B\).
Source: Proof and the Art of Mathematics, J. D. Hamkins
Source: Proof and the Art of Mathematics, J. D. Hamkins
Function composition
Discrete mathematics
Slides ⋅ Week 03 ⋅ 16th August, 2023
Induction

Source: Folklore
If there is a natural number with certain property, then there is a smallest number with that property.
Least-number principle
Every nonempty subset S of the positive integers
has a least element.
The set of positive integers does not contain any
infinite strictly decreasing sequences.
(AKA the well-ordering principle)
Let \(A\) be a set of integers with some \(b \in A\), and furthermore, that whenever \(n \in A\), then also \(n+1 \in A\).
Then \(A\) contains all integers above \(b\).
Principle of induction
Suppose \(\mathcal{P}\) is a property of an integer such that:
(1) \(\mathcal{P}(b)\) is true, and
(2) \(\mathcal{P}(n)\) being true implies that \(\mathcal{P}(n+1)\) is true.
Then \(\mathcal{P}\) holds for all integers above \(k\).
Assume that A is a set of natural numbers with the property that:
for every natural number n,
if every number smaller than n is in A, then n itself is in A.
Then every natural number is in A.
Principle of strong induction
Suppose \(\mathcal{P}\) is a property of an integer such that:
(1) \(\mathcal{P}(1)\) is true, and
(2) \(\mathcal{P}(k)\) being true for all \(k \leqslant n\) implies that \(\mathcal{P}(n+1)\) is true.
Then \(\mathcal{P}\) holds for all integers.
Least-number principle
\(\equiv\)
Principle of induction
\(\equiv\)
Principle of strong induction

Examples!
🎉
Nostalgia trip
\( \forall n \in \mathbb{N}, 1+3+5+\cdots+(2 n-1)=n^2\)
sum of the first \(n\) odd numbers...
\( \forall n \in \mathbb{N}, 1+2+4+\cdots+2^n=2^{n+1}-1.\)
sum of the first \(n\) powers of two...
\( \forall n \in \mathbb{N}, n^2 < 3^n.\)
\( \forall n \in \mathbb{N}, (n^3 - n)\) is a multiple of \(6\).
\( \forall n \in \mathbb{N}, (6^n - 1)\) is a multiple of \(5\).
Every natural number can be expressed as the sum of a unique set of distinct powers of 2.


A \(2^n \times 2^n\) square grid with one random tile removed can be completely tiled with L-shaped triminos.
A \(2^n \times 2^n\) square grid with one random tile removed can be completely tiled with L-shaped triminos.
Every positive integer can be represented uniquely as
the sum of one or more distinct Fibonacci numbers
in such a way that the sum
does not include any two consecutive Fibonacci numbers.
Zeckendorf's theorem
Every positive integer can be represented uniquely as
the sum of one or more distinct Fibonacci numbers
in such a way that the sum
does not include any two consecutive Fibonacci numbers.
Zeckendorf's theorem
\(F_j\)
\(F_{j+1}\)
\(n\)
A country has \(n\) cities and any two cities are connected by a one-way road.
There is a route that passes through every city.
\(\underbrace{~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~}\)
Induction Hypothesis 🎁
A country has \(n\) cities and any two cities are connected by a one-way road.
There is a route that passes through every city.
\(\underbrace{~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~}\)
Induction Hypothesis 🎁
If this road goes this way, we are done.
A country has \(n\) cities and any two cities are connected by a one-way road.
There is a route that passes through every city.
\(\underbrace{~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~}\)
Induction Hypothesis 🎁
So suppose not.
A country has \(n\) cities and any two cities are connected by a one-way road.
There is a route that passes through every city.
\(\underbrace{~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~}\)
Induction Hypothesis 🎁
If this road goes this way, we are done.
A country has \(n\) cities and any two cities are connected by a one-way road.
There is a route that passes through every city.
\(\underbrace{~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~}\)
Induction Hypothesis 🎁
So suppose not.
A country has \(n\) cities and any two cities are connected by a one-way road.
There is a route that passes through every city.
\(\underbrace{~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~}\)
Induction Hypothesis 🎁
An interim change of state is forced between consecutive cities...
A country has \(n\) cities and any two cities are connected by a one-way road.
There is a route that passes through every city.

Buckets Of Fish
This game is played with two players on the beach.
The game begins with finitely many buckets arranged in a row,
each bucket containing some finite number of fish,
with a large supply of additional fish available nearby, as many as needed, fresh off the boats.
Each player, in turn, takes a fish from one bucket and adds to each of the buckets to the left, if any, as many fish from the extra supply as he or she likes.
The winner is whoever takes the very last fish from the buckets,
leaving them empty.
1
2
3
4
5
6
7
8
12
11
10
9


































1
2
3
4
5
6
7
8
12
11
10
9

































1
2
3
4
5
6
7
8
12
11
10
9









































Every play of the game Buckets of Fish ends in finitely many moves.
All the fish in the buckets, including all the new fish that may have been added during play, will eventually run out by some finite stage during play.

Examples?
🤔

All integers of the form \(2n+1\) are divisible by 2.
Base Case. Easy as usual, left as an exercise.
Induction Step.
Source: Miklós Bóna, A Walk Through Combinatorics
WTS. \(2(n+1)+1\) is divisible by two.
Equivalently: \(2(n+1)+1\) \(-\) \((2n+1)\) is divisible by two.
\(2\) is divisible by two. ✔️

Every positive integer \(n\) is a whole lot less than 1,000,000.
Base Case. 1 is certainly a whole lot less than 1,000,000.
Source: Brilliant Wiki
If the positive integer \(k\) is a whole lot less than 1,000,000,
then \(k+1\), which is just slightly bigger than k,
is still a whole lot less than 1,000,000.
Hence, by mathematical induction, the statement is true for all positive integers. In particular, a billion is a whole lot less than a million.
Induction Step.

For every non-negative number \(n, 2 \times n=0\).
Base Case. \(n=0\). Clearly \(2 \times n=0\).
Induction Step. Say it holds for \(k\), and consider \(k+1\).
Write \(k+1=i+j\), where \(i\) and \(j\) are non-negative numbers. Then,
\(2(k+1)=2(i+j)=2 i+2 j=0+0=0.\)
Hence, by mathematical induction, the statement is true for all non-negative integers. In particular, \(2 \times 1=0\).
Source: Brilliant Wiki
Source: Brilliant Wiki

Claim. All positive integers are equal to 1.
Source: Notes
To prove the claim, we will prove by induction that, for all \(n \in \mathbb{N}\), the following statement holds:
Here \(\max (x, y)\) denotes the larger of the two numbers \(x\) and \(y\),
or the common value if both are equal.
If \(P(n)\) is true for all \(n \in \mathbb{N}\), then \(\max (1, n)=n\) for any positive integer \(n\).
Therefore it will follow that \(1=n\) for any positive integer \(n\).
Thus, all positive integers must be equal to 1.
\((P(n)). \quad\) For any \(x, y \in \mathbb{N}\), if \(\max (x, y)=n\), then \(x=y\).
Claim. All positive integers are equal to 1.
\((P(n)). \quad\) For any \(x, y \in \mathbb{N}\), if \(\max (x, y)=n\), then \(x=y\).
Base Case: When \(n=1\), the condition in \(P(1)\) becomes \(\max (x, y)=1\). But this forces \(x=1\) and \(y=1\), and hence \(x=y\).
Induction step: Let \(k \in \mathbb{N}\) be given and suppose \(P(k)\) is true. We seek to show that \(P(k+1)\) is true as well.
Let \(x, y \in \mathbb{N}\) be such that \(\max (x, y)=k+1\).
Then \(\max (x-1, y-1)=\max (x, y)-1=\) \((k+1)-1=k\).
By the induction hypothesis, it follows that \(x-1=y-1\),
and therefore \(x=y\). This proves \(P(k+1)\).

Claim. All cats have the same color.
Claim. For any positive integer \(n\),
any \(n\) cats always have the same color.
Base Case. For \(n = 1\), the statement is obviously true:
any one cat has the same color as itself.
Induction Step. Take \(n + 1\) cats, and line them up.
Then the first \(n\) cats must have the same color, say black, by the IH.
The last \(n\) cats also must have the same color, by the same IH, so they too must be black as we already have seen that all the first \(n\) cats were black, and that included the second, third, fourth,..., nth cats, which are also included among the last \(n\) cats.
Therefore, all \(n + 1\) cats are black.

Discrete mathematics
Slides ⋅ Week 04 ⋅ 22nd and 23rd August, 2023
Black Vienna
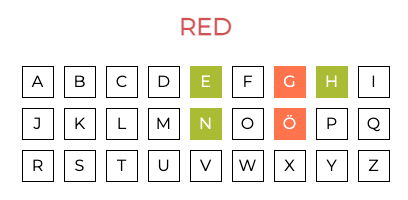
27 suspects, whose names are A,B,C,...,Z,Ö.
Ingredients
3 criminals, sometimes referred to as the Black Vienna ring. This is an unknown three-sized subset of A,B,C,...,Z,Ö.
3 investigators, who separately have alibis for 8 suspects each. These eight-sized subsets are disjoint from each other.
Black Vienna
The game progresses in a sequence of queries.
You are dealt three sets containing three suspects each.
Ingredients
You can choose any of these available sets, and pick an investigator (red, blue, or green) and ask them to tell you how many (not which!) of the three suspects they have alibis for.
So they can certify how many people from the given three
are NOT in the gang: 0, 1, 2, or 3.
Black Vienna
Black Vienna
Link to Play (us v/s the machine)
Link to Play (teams of threre)

if
and

then:

if
then:

Proposition. A proposition is a declarative sentence (that is, a sentence that declares a fact) that is either true or false, but not both.
We use letters to denote propositional variables.
The conventional letters used for propositional variables are p, q, r, s, ...
U belongs to the BV ring.
The truth value of a proposition is true (T) if it is a true proposition.
The truth value of a proposition is false (F), if it is a false proposition.
Propositions that cannot be expressed in terms of simpler propositions are called atomic propositions.

p
q
p 🤝 q
T
T
T
T
F
F
F
F
F
F
F
F
Make Your Own Truth Tables!
Always False
p
q
p 🤝 q
T
T
T
T
F
F
F
F
F
F
F
T
Make Your Own Truth Tables!
Negation of OR (NOR)
p
q
p 🤝 q
T
T
T
T
F
F
F
F
F
F
T
F
Make Your Own Truth Tables!
q is right and p is wrong [CONVERSE NONIMPLICATION]
p
q
p 🤝 q
T
T
T
T
F
F
F
F
F
F
T
T
Make Your Own Truth Tables!
p is false.
p
q
p 🤝 q
T
T
T
T
F
F
F
F
F
T
F
F
Make Your Own Truth Tables!
p is right and q is wrong MATERIAL NONIMPLICATION
p
q
p 🤝 q
T
T
T
T
F
F
F
F
F
T
F
T
Make Your Own Truth Tables!
q is false.
p
q
p 🤝 q
T
T
T
T
F
F
F
F
F
T
T
F
Make Your Own Truth Tables!
Exclusive OR (XOR) | Parity
p
q
p 🤝 q
T
T
T
T
F
F
F
F
F
T
T
T
Make Your Own Truth Tables!
Negation of AND (NAND)
p
q
p 🤝 q
T
T
T
T
F
F
F
F
T
F
F
F
Make Your Own Truth Tables!
AND
p
q
p 🤝 q
T
T
T
T
F
F
F
F
T
F
F
T
Make Your Own Truth Tables!
Negation of Exclusive OR (NOR) | p IFF q
p
q
p 🤝 q
T
T
T
T
F
F
F
F
T
F
T
F
Make Your Own Truth Tables!
q is true.
p
q
p 🤝 q
T
T
T
T
F
F
F
F
T
F
T
T
Make Your Own Truth Tables!
IMPLICATION It is not the case that p is true and q is not.
p
q
p 🤝 q
T
T
T
T
F
F
F
F
T
T
F
F
Make Your Own Truth Tables!
p is true.
p
q
p 🤝 q
T
T
T
T
F
F
F
F
T
T
F
T
Make Your Own Truth Tables!
Converse [i.e, q implies p]
p
q
p 🤝 q
T
T
T
T
F
F
F
F
T
T
T
F
Make Your Own Truth Tables!
OR
p
q
p 🤝 q
T
T
T
T
F
F
F
F
T
T
T
T
Make Your Own Truth Tables!
Always True
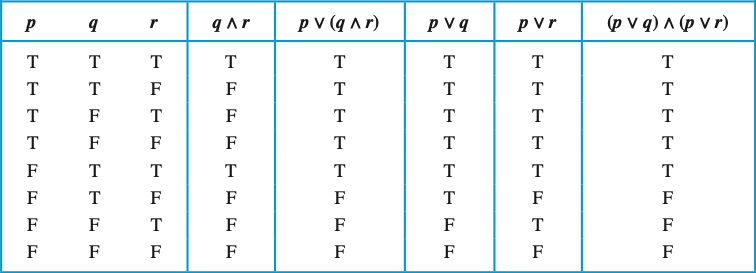
Demonstration of Equivalence between
\(p \lor (q \land r)\) and \((p \lor q) \land (p \lor r)\)
Source: Rosen, 8th Edition, p. 28.
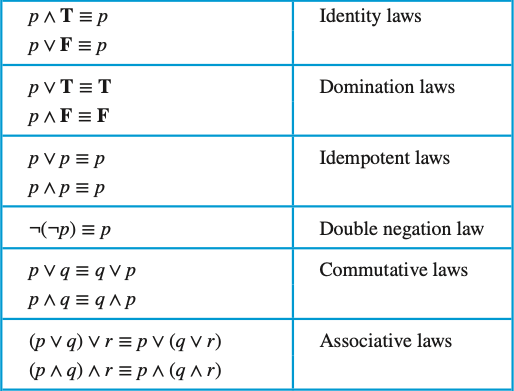
Source: Rosen, 8th Edition, p. 29.

Source: Rosen, 8th Edition, p. 29.
A compound proposition that is always true,
no matter what the truth values of the propositional variables that occur in it,
is called a tautology.
A compound proposition that is always false
is called a contradiction.
A compound proposition that is
neither a tautology nor a contradiction
is called a contingency.
Always T/F
A compound proposition is satisfiable if there is an assignment of truth values to its variables that makes it true
(that is, when it is a tautology or a contingency).
When no such assignments exists, that is, when the compound proposition is false for all assignments of truth values to its variables, the compound proposition is unsatisfiable.
Satisfiability
Note that a compound proposition is unsatisfiable if and only if its negation is true for all assignments of truth values to the variables, that is, if and only if its negation is a tautology.
\(p_A := \) A belongs to the blue team.
\(p_B := \) B belongs to the blue team.
\(p_C := \) C belongs to the blue team.
\(\vdots\)
\(p_Z := \) Z belongs to the blue team.
\(q_A := \) A belongs to the red team.
\(q_B := \) B belongs to the red team.
\(q_C := \) C belongs to the red team.
\(\vdots\)
\(q_Z := \) Z belongs to the red team.
\(r_A := \) A belongs to the green team.
\(r_B := \) B belongs to the green team.
\(r_C := \) C belongs to the green team.
\(\vdots\)
\(r_Z := \) Z belongs to the green team.
\(s_A := \) A belongs to the Black Vienna gang.
\(s_B := \) B belongs to the Black Vienna gang.
\(s_C := \) C belongs to the Black Vienna gang.
\(\vdots\)
\(s_Z := \) Z belongs to the Black Vienna gang.
27 * 4 = 108 atomic propositions 🎉
\(p_A \implies (\neg q_A \land \neg r_A \land \neg s_A)\)
\(q_A \implies (\neg p_A \land \neg r_A \land \neg s_A)\)
\(r_A \implies (\neg p_A \land \neg q_A \land \neg s_A)\)
\(s_A \implies (\neg p_A \land \neg q_A \land \neg r_A)\)
Everyone belongs to at most one team.
\(p_Z \implies (\neg q_Z \land \neg r_Z \land \neg s_Z)\)
\(q_Z \implies (\neg p_Z \land \neg r_Z \land \neg s_Z)\)
\(r_Z \implies (\neg p_Z \land \neg q_Z \land \neg s_Z)\)
\(s_Z \implies (\neg p_Z \land \neg q_Z \land \neg r_Z)\)
\(\ldots\)
\(\ldots\)
\(\ldots\)
\(\ldots\)
\(p_A \lor q_A \lor r_A \lor s_A\)
Everyone belongs to at least one team.
\(p_B \lor q_B \lor r_B \lor s_B\)
\(p_Z \lor q_Z \lor r_Z \lor s_Z\)
\(\vdots\)
\(\cdots \large{\color{indianred}\lor} (p_A \land p_B \land p_C \land p_D \land p_W \land p_X \land p_Y \land p_Z) {\color{indianred}\lor} \cdots \)
\(\cdots \large{\color{indianred}\lor} \underbrace{(q_A \land q_B \land q_C \land q_D \land q_W \land q_X \land q_Y \land q_Z)}_{\text{a typical 8-sized subset of} \{ \text{ABCDEFGHIJKLMNOÖPQRSTUVQXYZ} \}} {\color{indianred}\lor} \cdots\)
\(\cdots\large{\color{indianred}\lor} (r_A \land r_B \land r_C \land r_D \land r_W \land r_X \land r_Y \land r_Z){\color{indianred}\lor} \cdots \)
\(\huge{\land}\)
\(\cdots \large{\color{indianred}\lor} (s_D \land s_M \land s_E){\color{indianred}\lor}\cdots\)
\(\huge{\land}\)
\(\huge{\land}\)
Any assignment of truth values to the 108 atomic variables will correspond to a valid partition of the population into R, B, G and BV.
We are looking for a specific partition among these.


\(\Huge{\oplus(q_E, q_G, q_Ö)}\)
\(\Huge{q_E \land q_H \land q_N}\)

Source: Rosen, 8th Edition, p. 76.
Sometimes, propositional logic is not expressive enough.
Suppose you want to assert that there are at least 5 primes among the numbers \(\{1,2,\ldots,100\}\).
Let \(p_k\) denote the proposition that \(k\) is a prime.
\(\cdots \lor \underbrace{( p_3 \land p_7 \land p_{42} \land p_2 \land p_9 )}_{\text{A typical 5-sized subset of} \{1,2,\ldots,100\}.} \lor \cdots\)
Sometimes, propositional logic is not expressive enough.
Suppose you want to assert that
there are infinitely many primes...?
Predicate Logic
Predicate Logic
A statement involving the \(n\) variables
\((x_1, \ldots x_n)\)
can be denoted by
\(P(x_1, \ldots, x_n)\).
\(P(x_1,x_2) := x_1 > x_2 + 1024\)
Predicate Logic
The universal quantification of \(P(x)\) is the statement:
\(P(x)\) for all values of \(x\) in the domain.
The notation \(\forall xP(x)\) denotes the universal quantification of \(P(x)\).
Can be falsified with a single counterexample.
\(P(x) := x \text{ can be written as a sum of two odd numbers}.\)
\(\forall x P(x)\) is false because it is not true for \(x = 3\).
Predicate Logic
The existential quantification of \(P(x)\) is the statement:
There exists an element x in the domain such that \(P(x)\).
The notation \(\exists xP(x)\) denotes the existential quantification of \(P(x)\).
Can be justified with a single counterexample.
\(P(x) := x \text{ can be written as a sum of two odd numbers}.\)
\(\exists x P(x)\) is true because it is true for \(x = 2\).
De Morgan's Laws for Quantifiers.

Source: Rosen, 8th Edition, p. 51.
Lewis CaRroll Examples
All lions are fierce.
Some lions do not drink coffee.
Some fierce creatures do not drink coffee.
Source: Rosen, 8th Edition, p. 80.
Common Fallacy
\(q\)
\(p \rightarrow q\)
\(p\)
\(\neg p\)
\(p \rightarrow q\)
\(\neg q\)
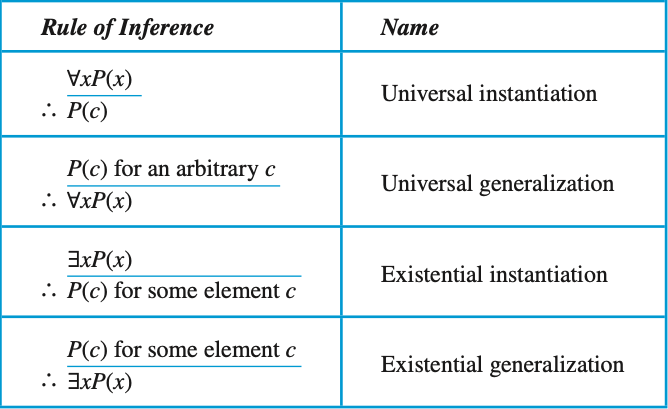
\(\forall x ~ P(x) \rightarrow Q(x)\)
\(\neg P(y)\)
\(\neg Q(y)\)
People who play chess are smart.
If I am bad at chess then I am stupid.
\(P(x)\) := \(x\) plays chess.
\(Q(x)\) := \(x\) is smart.
\(P(y) \rightarrow Q(y)\)
\(\neg P(y)\)
\(\neg Q(y)\)
People who play chess are smart.
If I am bad at chess then I am stupid.
\(P(x)\) := \(x\) plays chess.
\(Q(x)\) := \(x\) is smart.
If you get 100% on the final, then you will get an A.
- Not Me 👀
You don't get 100% on the final.
What can you say about your grade?

Source: Folklore; image from brilliant.org logic puzzles
1. If Jyothi is watching television, so is Tanvi.
2. Either Gaurav or Manish, or both of them, are watching television.
3. Either Tanvi or Sharda, but not both, is watching television.
4. Gaurav and Sharda are either both watching or both not watching television.
5. If Manish is watching television, then Jyothi and Gaurav are also watching.
Who is watching television and who is not?
1. \(J \rightarrow T\)
2. Either Gaurav or Manish, or both of them, are watching television.
3. Either Tanvi or Sharda, but not both, is watching television.
4. Gaurav and Sharda are either both watching or both not watching television.
5. If Manish is watching television, then Jyothi and Gaurav are also watching.
Who is watching television and who is not?
1. \(J \rightarrow T\)
2. \(G \lor M\)
3. Either Tanvi or Sharda, but not both, is watching television.
4. Gaurav and Sharda are either both watching or both not watching television.
5. If Manish is watching television, then Jyothi and Gaurav are also watching.
Who is watching television and who is not?
1. \(J \rightarrow T\)
2. \(G \lor M\)
3. \(T \oplus S\)
4. Gaurav and Sharda are either both watching or both not watching television.
5. If Manish is watching television, then Jyothi and Gaurav are also watching.
Who is watching television and who is not?
1. \(J \rightarrow T\)
2. \(G \lor M\)
3. \(T \oplus S\)
4. \(G {\color{indianred}\oplus} S\)
5. If Manish is watching television, then Jyothi and Gaurav are also watching.
Who is watching television and who is not?
1. \(J \rightarrow T\)
2. \(G \lor M\)
3. \(T \oplus S\)
4. \(G {\color{indianred}\oplus} S\)
5. \(M \rightarrow (J \land G) \)
Who is watching television and who is not?
extras
A logician's wife is having a baby.
The doctor immediately hands the newborn to the dad.
The wife says, 'Is it a boy or a girl?'
The logician says, 'Yes.'
Three logicians walk into a bar
The bartender asks: "Do you all want a drink?"
The first logician says: "I don't know."
The second logician says: "I don't know."
The third logician says: "Yes."
Blue Eyes
a puzzle
Source. Terry Tao's blog
See Also: XKCD
There is an island upon which a tribe resides.
The tribe consists of 1000 people, with various eye colours.
Yet, their religion forbids them to know their own eye color,
or even to discuss the topic; thus, each resident can (and does) see the eye colors of all other residents, but has no way of discovering his or her own (there are no reflective surfaces).
If a tribesperson does discover his or her own eye color,
then their religion compels them to commit ritual suicide
at noon the following day in the village square for all to witness.
All the tribespeople are highly logical and devout, and they all know that each other is also highly logical and devout (and they all know that they all know that each other is highly logical and devout, and so forth).
Of the 1000 islanders, it turns out that
100 of them have blue eyes and 900 of them have brown eyes,
although the islanders are not initially aware of these statistics
(each of them can of course only see 999 of the 1000 tribespeople).
One day, a blue-eyed foreigner visits to the island and wins the complete trust of the tribe.
One evening, he addresses the entire tribe to thank them for their hospitality.
😬
However, not knowing the customs, the foreigner makes the mistake of mentioning eye color in his address, remarking “how unusual it is to see another blue-eyed person like myself in this region of the world”.
What effect, if anything, does this faux pas have on the tribe?
Argument 1
The foreigner has no effect, because his comments do not tell the tribe anything that they do not already know (everyone in the tribe can already see that there are several blue-eyed people in their tribe).
Argument 2
100 days after the address, all the blue eyed people commit suicide.
This is proven as a special case of:
Suppose that the tribe had n blue-eyed people for some positive integer n.
Then n days after the traveller’s address, all n blue-eyed people commit suicide.
Proof: We induct on n.
When \(n=1\), the single blue-eyed person realizes that the traveler is referring to him or her, and thus commits suicide on the next day.
Now suppose inductively that n is larger than 1.
Each blue-eyed person will reason as follows: “If I am not blue-eyed, then there will only be n-1 blue-eyed people on this island, and so they will all commit suicide n-1 days after the traveler’s address”.
But when n-1 days pass, none of the blue-eyed people do so
(because at that stage they have no evidence that they themselves are blue-eyed).
After nobody commits suicide on the \((n-1)^{st}\) day, each of the blue eyed people then realizes that they themselves must have blue eyes, and will then commit suicide on the \(n^{th}\) day.
1. \(A \rightarrow B\)
2. Either Dale or Ellsworth, or both of them, are watching television.
3. Either Beryl or Cleo, but not both, is watching television.
4. Dale and Cleo are either both watching or both not watching television.
5. If Ellsworth is watching television, then Abner and Dale are also watching.
Who is watching television and who is not?
1. \(A \rightarrow B\)
2. \(D \lor E\)
3. Either Beryl or Cleo, but not both, is watching television.
4. Dale and Cleo are either both watching or both not watching television.
5. If Ellsworth is watching television, then Abner and Dale are also watching.
Who is watching television and who is not?
1. \(A \rightarrow B\)
2. \(D \lor E\)
3. \(B \oplus C\)
4. Dale and Cleo are either both watching or both not watching television.
5. If Ellsworth is watching television, then Abner and Dale are also watching.
Who is watching television and who is not?
1. \(A \rightarrow B\)
2. \(D \lor E\)
3. \(B \oplus C\)
4. \(D {\color{indianred}\oplus} C\)
5. If Ellsworth is watching television, then Abner and Dale are also watching.
Who is watching television and who is not?
1. \(A \rightarrow B\)
2. \(D \lor E\)
3. \(B \oplus C\)
4. \(D {\color{indianred}\oplus} C\)
5. \(E \rightarrow A \land D\)
Who is watching television and who is not?
Discrete mathematics
Slides ⋅ Week 05 ⋅ 29th and 30th August, 2023
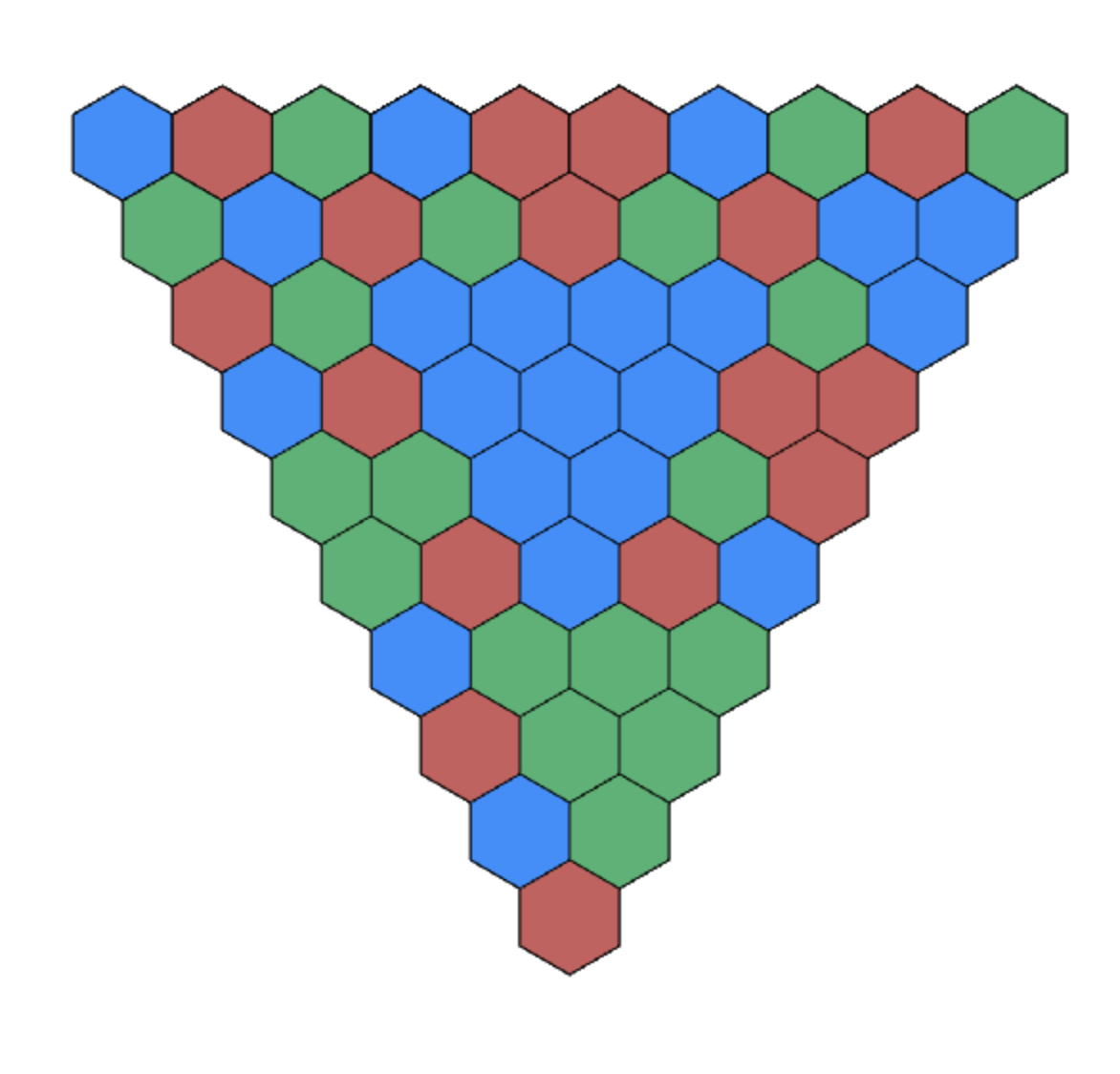
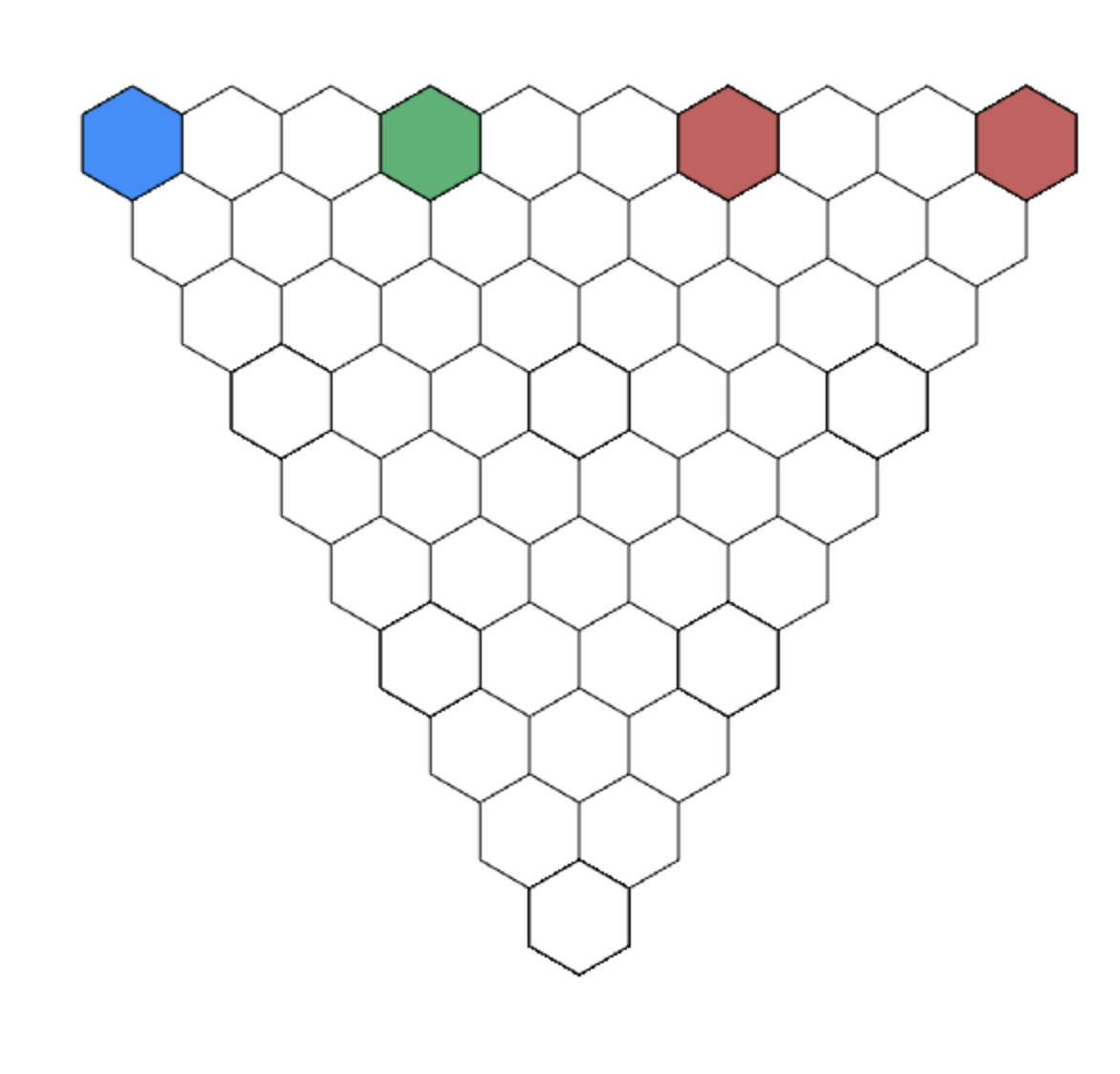
A TILING GAME
A Tiling Game

Source: Mathologer

Source: Mathologer
Corners determine the bottom cell for n = 4.
Using this, we can show that the corners determine the bottom cell for n = 10 as well.
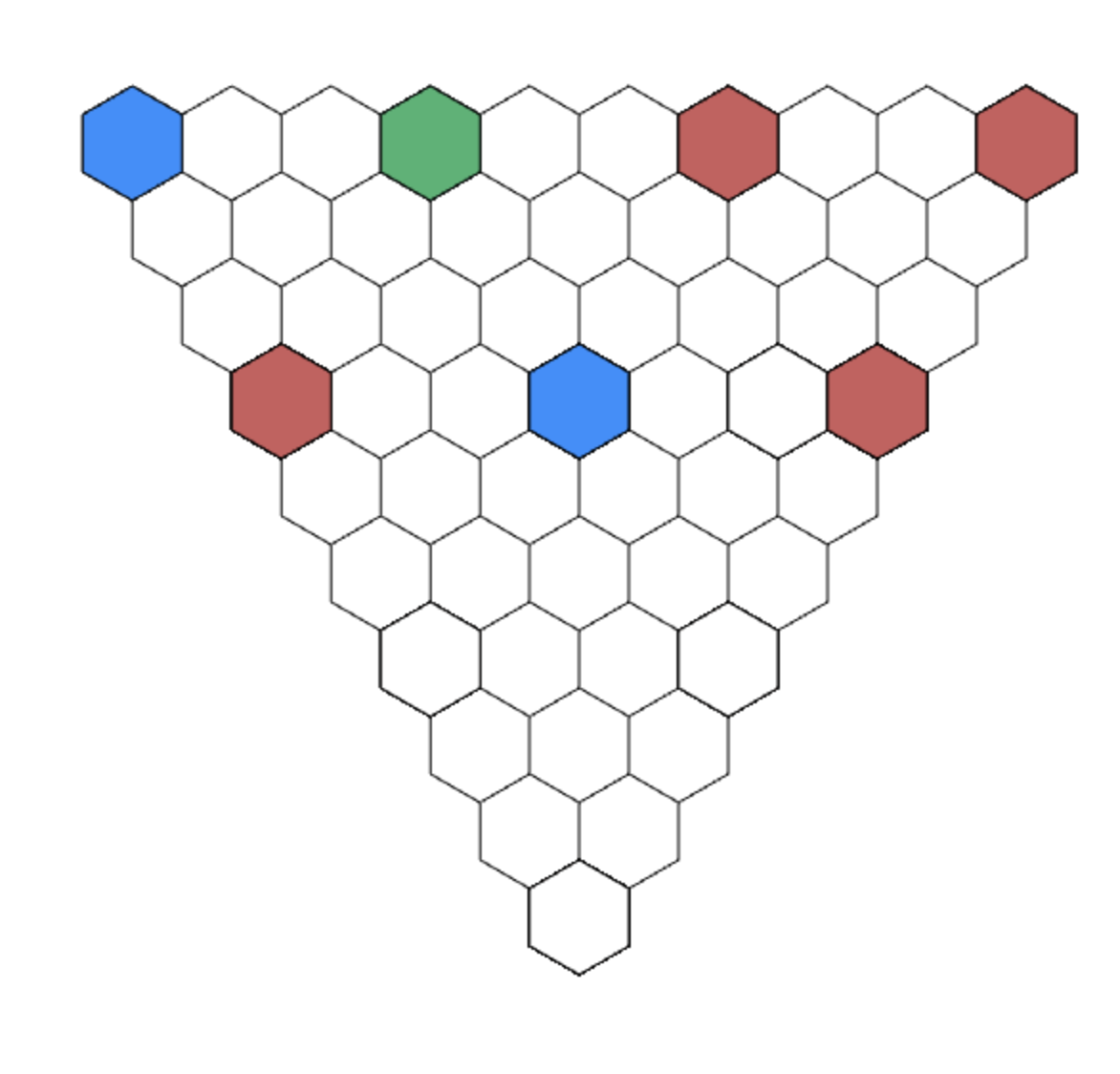
Using this, we can show that the corners determine the bottom cell for n = 10 as well.
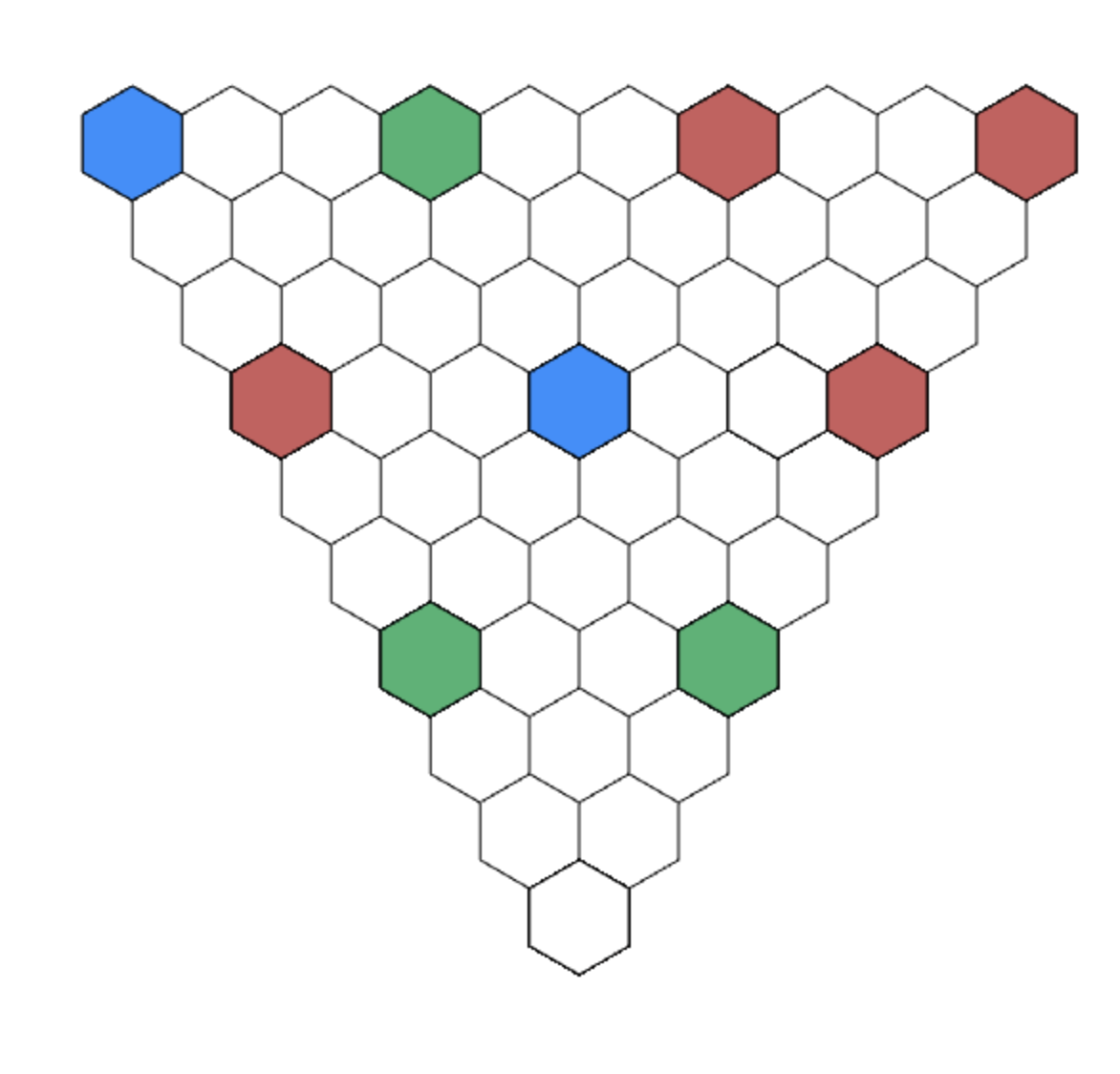
Using this, we can show that the corners determine the bottom cell for n = 10 as well.
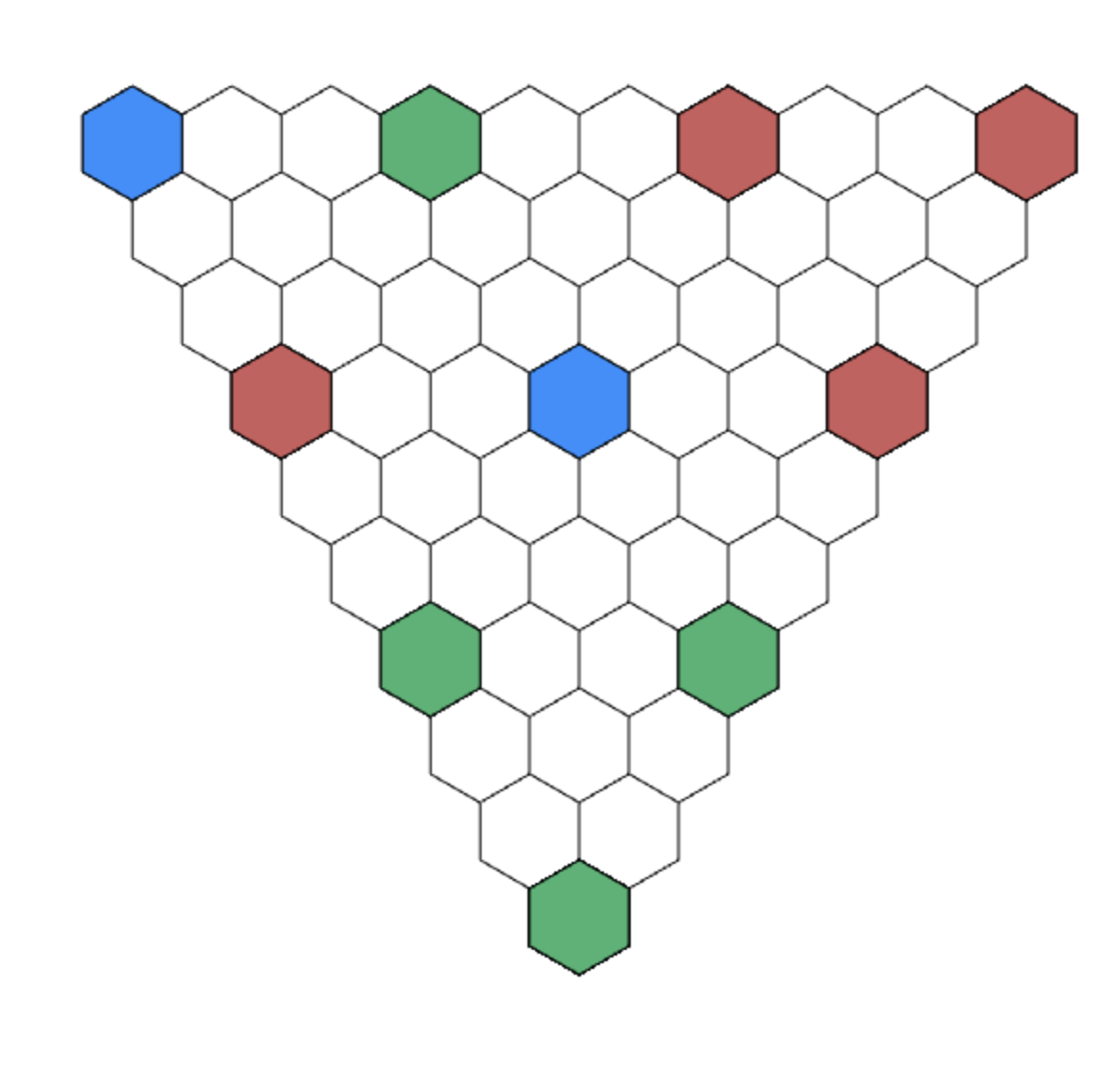
Using this, we can show that the corners determine the bottom cell for n = 10 as well.
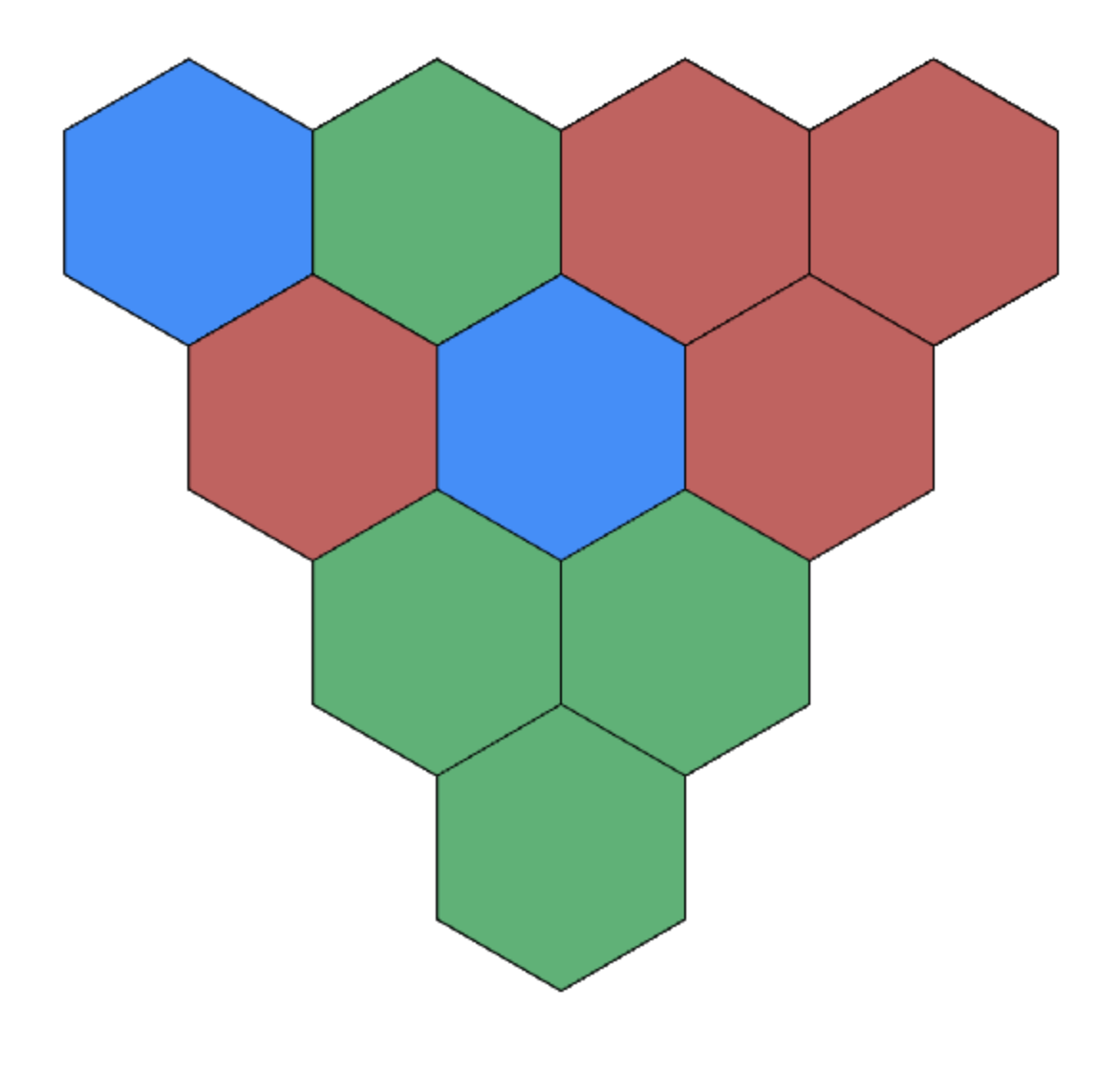
Using this, we can show that the corners determine the bottom cell for n = 10 as well.
PASCAL's TRIANGLE
1
0
0
0
0
1
0
0
0
0
1
0
0
0
0
1
1
1
1
1
2
3
3
1
1
1
1
4
4
6
1
1
5
5
10
10
1
1
6
6
15
15
20
1
1
7
7
21
21
35
35
1
1
8
8
28
28
56
56
70
1
1
9
9
36
36
84
84
126
126
1
1
10
10
45
45
120
120
210
210
252
Claim. The \(i\)-th non-zero entry
in the \(n\)-th row of the Pascal's Triangle is
\({n-1 \choose i-1}\).
Proof. For \(i = 1\), the statement is true for any \(n\).
The statement is also true for \(n = 1\).
For \(n > 1, i > 1\), the \(i\)-th non-zero entry
in the \(n\)-th row of the Pascal's Triangle is:
[\(i\)-th non-zero entry in the \((n-1)\)-th row]
+
[\((i-1)\)-th non-zero entry in the \((n-1)\)-th row]
Claim. The \(i\)-th non-zero entry
in the \(n\)-th row of the Pascal's Triangle is
\({n-1 \choose i-1}\).
Proof. For \(i = 1\), the statement is true for any \(n\).
The statement is also true for \(n = 1\).
For \(n > 1, i > 1\), the \(i\)-th non-zero entry
in the \(n\)-th row of the Pascal's Triangle is:
\({n-2 \choose i-1}\)
+
\({n-2 \choose i-2}\)
\({n \choose k}\) = \({n-1 \choose k}\) + \({n-1 \choose k-1}\)
\(\underbrace{~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~}_{k}\)
\(\underbrace{~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~}_{k-1}\)
\(\begin{aligned} ~ & \left(\begin{array}{c}n \\ r\end{array}\right) =\frac{n!}{(n-r)!(r)!} \\~\\ & =\frac{(n{\color{IndianRed}-r+r}) \cdot (n-1)!}{(n-r)!(r)!} \\~\\ & =\frac{(r)(n-1)!}{(n-r)!(r)!}+ \frac{(n-r)(n-1)!}{(n-r)!(r)!} \\~\\ & =\frac{(n-1)!}{(n-r)!(r-1)!}+\frac{(n-1)!}{(n-r-1)!r!} \\~\\ & = \left(\begin{array}{c}n-1 \\ r-1\end{array}\right)+\left(\begin{array}{c}n-1 \\ r\end{array}\right) \cdot \end{aligned}\)
Claim. The \(i\)-th non-zero entry
in the \(n\)-th row of the Pascal's Triangle is
\({n-1 \choose i-1}\).
Proof. For \(i = 1\), the statement is true for any \(n\).
The statement is also true for \(n = 1\).
For \(n > 1, i > 1\), the \(i\)-th non-zero entry
in the \(n\)-th row of the Pascal's Triangle is:
\({n-2 \choose i-1}\)
+
\({n-2 \choose i-2}\)
...and we are done 🎉
1
1
1
1
1
2
3
3
1
1
1
1
4
4
6
1
1
5
5
10
10
1
1
6
6
15
15
20
1
1
7
7
21
21
35
35
1
1
8
8
28
28
56
56
70
1
1
9
9
36
36
84
84
126
126
1
1
10
10
45
45
120
120
210
210
252
1
1
1
1
1
\({2 \choose 1}\)
\({3 \choose 1}\)
\({3 \choose 2}\)
1
1
1
1
\({4 \choose 1}\)
\({4 \choose 3}\)
6
1
1
\({5 \choose 1}\)
\({5 \choose 4}\)
10
10
1
1
\({6 \choose 1}\)
\({6 \choose 5}\)
15
15
20
1
1
\({7 \choose 6}\)
\({7 \choose 1}\)
21
21
35
35
1
1
\({8 \choose 7}\)
\({8 \choose 1}\)
28
28
56
56
70
1
1
\({9 \choose 8}\)
\({9 \choose 1}\)
36
36
84
84
126
126
1
1
\({10 \choose 9}\)
\({10 \choose 1}\)
45
45
120
120
210
210
252
1
1
1
1
1
\({2 \choose 1}\)
\({3 \choose 1}\)
\({3 \choose 2}\)
1
1
1
1
\({4 \choose 1}\)
\({4 \choose 3}\)
\({4 \choose 2}\)
1
1
\({5 \choose 1}\)
\({5 \choose 4}\)
\({5 \choose 2}\)
\({5 \choose 3}\)
1
1
\({6 \choose 1}\)
\({6 \choose 5}\)
\({6 \choose 2}\)
\({6 \choose 4}\)
20
1
1
\({7 \choose 6}\)
\({7 \choose 1}\)
\({7 \choose 2}\)
\({7 \choose 5}\)
35
35
1
1
\({8 \choose 7}\)
\({8 \choose 1}\)
\({8 \choose 2}\)
\({8 \choose 6}\)
56
56
70
1
1
\({9 \choose 8}\)
\({9 \choose 1}\)
\({9 \choose 2}\)
\({9 \choose 7}\)
84
84
126
126
1
1
\({10 \choose 9}\)
\({10 \choose 1}\)
\({10 \choose 2}\)
\({10 \choose 8}\)
120
120
210
210
252
1
1
1
1
1
\({2 \choose 1}\)
\({3 \choose 1}\)
\({3 \choose 2}\)
1
1
1
1
\({4 \choose 1}\)
\({4 \choose 3}\)
\({4 \choose 2}\)
1
1
\({5 \choose 1}\)
\({5 \choose 4}\)
\({5 \choose 2}\)
\({5 \choose 3}\)
1
1
\({6 \choose 1}\)
\({6 \choose 5}\)
\({6 \choose 2}\)
\({6 \choose 4}\)
\({6 \choose 3}\)
1
1
\({7 \choose 6}\)
\({7 \choose 1}\)
\({7 \choose 2}\)
\({7 \choose 5}\)
\({7 \choose 3}\)
\({7 \choose 4}\)
1
1
\({8 \choose 7}\)
\({8 \choose 1}\)
\({8 \choose 2}\)
\({8 \choose 6}\)
\({8 \choose 3}\)
\({8 \choose 5}\)
70
1
1
\({9 \choose 8}\)
\({9 \choose 1}\)
\({9 \choose 2}\)
\({9 \choose 7}\)
\({9 \choose 3}\)
\({9 \choose 6}\)
126
126
1
1
\({10 \choose 9}\)
\({10 \choose 1}\)
\({10 \choose 2}\)
\({10 \choose 8}\)
\({10 \choose 3}\)
\({10 \choose 7}\)
210
210
252
1
1
1
1
1
\({2 \choose 1}\)
\({3 \choose 1}\)
\({3 \choose 2}\)
1
1
1
1
\({4 \choose 1}\)
\({4 \choose 3}\)
\({4 \choose 2}\)
1
1
\({5 \choose 1}\)
\({5 \choose 4}\)
\({5 \choose 2}\)
\({5 \choose 3}\)
1
1
\({6 \choose 1}\)
\({6 \choose 5}\)
\({6 \choose 2}\)
\({6 \choose 4}\)
\({6 \choose 3}\)
1
1
\({7 \choose 6}\)
\({7 \choose 1}\)
\({7 \choose 2}\)
\({7 \choose 5}\)
\({7 \choose 3}\)
\({7 \choose 4}\)
1
1
\({8 \choose 7}\)
\({8 \choose 1}\)
\({8 \choose 2}\)
\({8 \choose 6}\)
\({8 \choose 3}\)
\({8 \choose 5}\)
\({8 \choose 4}\)
1
1
\({9 \choose 8}\)
\({9 \choose 1}\)
\({9 \choose 2}\)
\({9 \choose 7}\)
\({9 \choose 3}\)
\({9 \choose 6}\)
\({9 \choose 4}\)
\({9 \choose 5}\)
1
1
\({10 \choose 9}\)
\({10 \choose 1}\)
\({10 \choose 2}\)
\({10 \choose 8}\)
\({10 \choose 3}\)
\({10 \choose 7}\)
\({10 \choose 4}\)
\({10 \choose 6}\)
252
1
1
1
1
1
\({2 \choose 1}\)
\({3 \choose 1}\)
\({3 \choose 2}\)
1
1
1
1
\({4 \choose 1}\)
\({4 \choose 3}\)
\({4 \choose 2}\)
1
1
\({5 \choose 1}\)
\({5 \choose 4}\)
\({5 \choose 2}\)
\({5 \choose 3}\)
1
1
\({6 \choose 1}\)
\({6 \choose 5}\)
\({6 \choose 2}\)
\({6 \choose 4}\)
\({6 \choose 3}\)
1
1
\({7 \choose 6}\)
\({7 \choose 1}\)
\({7 \choose 2}\)
\({7 \choose 5}\)
\({7 \choose 3}\)
\({7 \choose 4}\)
1
1
\({8 \choose 7}\)
\({8 \choose 1}\)
\({8 \choose 2}\)
\({8 \choose 6}\)
\({8 \choose 3}\)
\({8 \choose 5}\)
\({8 \choose 4}\)
1
1
\({9 \choose 8}\)
\({9 \choose 1}\)
\({9 \choose 2}\)
\({9 \choose 7}\)
\({9 \choose 3}\)
\({9 \choose 6}\)
\({9 \choose 4}\)
\({9 \choose 5}\)
1
1
\({10 \choose 9}\)
\({10 \choose 1}\)
\({10 \choose 2}\)
\({10 \choose 8}\)
\({10 \choose 3}\)
\({10 \choose 7}\)
\({10 \choose 4}\)
\({10 \choose 6}\)
\({10 \choose 5}\)
1
1
1
1
1
2
3
3
1
1
1
1
4
4
6
1
1
5
5
10
10
1
1
6
6
15
15
20
1
1
7
7
21
21
35
35
1
1
8
8
28
28
56
56
70
1
1
9
9
36
36
84
84
126
126
1
1
10
10
45
45
120
120
210
210
252
2
+
=
4
=
+
+
8
=
+
+
+
=
16
+
+
+
+
=
32
+
+
+
+
+
=
64
+
+
+
+
+
+
=
128
+
+
+
+
+
+
+
1
1
1
1
1
2
3
3
1
1
1
1
4
4
6
1
1
5
5
10
10
1
1
6
6
15
15
20
1
1
7
7
21
21
35
35
1
1
8
8
28
28
56
56
70
1
1
9
9
36
36
84
84
126
126
1
1
10
10
45
45
120
120
210
210
252
1
1
1
1
1
2
3
3
1
1
1
1
4
4
6
1
1
5
5
10
10
1
1
6
6
15
15
20
1
1
7
7
21
21
35
35
1
1
8
8
28
28
56
56
70
1
1
9
9
36
36
84
84
126
126
1
1
10
10
45
45
120
120
210
210
252
1
1
1
1
1
2
3
3
1
1
1
1
4
4
6
1
1
5
5
10
10
1
1
6
6
15
15
20
1
1
7
7
21
21
35
35
1
1
8
8
28
28
56
56
70
1
1
9
9
36
36
84
84
126
126
1
1
10
10
45
45
120
120
210
210
252
The Hockey Stick Identity
\(\sum_{k=r}^n\left(\begin{array}{l}k \\ r\end{array}\right)=\left(\begin{array}{l}n+1 \\ r+1\end{array}\right)\)
\(\underbrace{r = 1: {1 \choose 1} + {2 \choose 1} + \cdots + {n \choose 1} = {n+1 \choose 2}}_{\text{Sum of the first } n \text{ natural numbers.}}\)
\(\underbrace{\sum_{j=0}^m\left(\begin{array}{c}j+q-2 \\ q-2\end{array}\right)}_{\text{isolate the last bin}}=\underbrace{\left(\begin{array}{c}m+q-1 \\ q-1\end{array}\right)}_{\text{stars and bars argument}}\)
#of ways of distributing m objects into q bins:
Let \(k=j+q−2\), let \(r=q−2\), and let \(n=m+q−2\).
The Hockey Stick Identity
\(\sum_{k=r}^n\left(\begin{array}{l}k \\ r\end{array}\right)=\left(\begin{array}{l}n+1 \\ r+1\end{array}\right)\)
The right-hand side clearly counts the number of \(r+1\)-element subsets of \([n+1]\).
The left-hand side counts the same,
separated into cases according to the largest entry.
That is:
there are \(\left(\begin{array}{l}r \\ r\end{array}\right)\) subsets of \([n+1]\) that have
\(r+1\) elements whose largest element is \(r+1\);
there are \(\left(\begin{array}{c}r+1 \\ r\end{array}\right)\) subsets of \([n+1]\) that have
\(r+1\) elements whose largest element is \(r+2\), and so on.
Source: Bona, A Walk Through Combinatorics, Theorem 4.5
The Hockey Stick Identity
\(\sum_{k=r}^n\left(\begin{array}{l}k \\ r\end{array}\right)=\left(\begin{array}{l}n+1 \\ r+1\end{array}\right)\)
The right-hand side clearly counts the number of \(k+1\)-element subsets of \([n+1]\).
The left-hand side counts the same,
separated into cases according to the largest entry.
In general, there are \(\left(\begin{array}{c}r+i \\ r\end{array}\right)\) subsets of \([n+1]\)
that have \(r+1\) elements whose largest element is \(r+i+1\),
for all \(i \leq k-r\).
Indeed, if the largest element of such a subset is \(r+i+1\), then its remaining \(r\) elements must form a subset of \([r+i]\).
Source: Bona, A Walk Through Combinatorics, Theorem 4.5
The Hockey Stick Identity
\(\sum_{k=r}^n\left(\begin{array}{l}k \\ r\end{array}\right)=\left(\begin{array}{l}n+1 \\ r+1\end{array}\right)\)
\(\sum_{k=r}^{n+1}\left(\begin{array}{l}k \\ r\end{array}\right) =\left(\begin{array}{c}n+1 \\ r\end{array}\right)+\underbrace{\left(\sum_{k=r}^{n}\left(\begin{array}{l}k \\ r\end{array}\right) \right)}_{\text{Induction Hypothesis}}\)
\(\sum_{k=r}^{n+1}\left(\begin{array}{l}k \\ r\end{array}\right) =\left(\begin{array}{c}n+1 \\ r\end{array}\right)+\left(\begin{array}{c}n+1 \\ r+1\end{array}\right)\)
Assume:
\(\sum_{k=r}^{n+1}\left(\begin{array}{l}k \\ r\end{array}\right) =\left(\begin{array}{c}n+2 \\ r+1\end{array}\right)\)
1
1
1
1
1
2
3
3
1
1
1
1
4
4
6
1
1
5
5
10
10
1
1
6
6
15
15
20
1
1
7
7
21
21
35
35
1
1
8
8
28
28
56
56
70
1
1
9
9
36
36
84
84
126
126
1
1
10
10
45
45
120
120
210
210
252
1
1
1
1
1
0
1
1
1
1
1
1
0
0
0
1
1
1
1
0
0
1
1
0
0
1
1
0
1
1
1
1
1
1
1
1
1
1
0
0
0
0
0
0
0
1
1
1
1
0
0
0
0
0
0
1
1
0
0
1
1
0
0
0
0
0
Sierpinski triangle

Source: Wikipedia
1
1
1
1
1
2
3
3
1
1
1
1
4
4
6
1
1
5
5
10
10
1
1
6
6
15
15
20
1
1
7
7
21
21
35
35
1
1
8
8
28
28
56
56
70
1
1
9
9
36
36
84
84
126
126
1
1
10
10
45
45
120
120
210
210
252
1
1
1
1
1
2
0
0
1
1
1
1
1
1
0
1
1
2
2
1
1
1
1
0
0
0
0
2
1
1
1
1
0
0
2
2
1
1
2
2
1
1
2
2
1
1
1
0
0
0
0
0
0
0
0
1
1
1
1
0
0
0
0
0
0
0
1
1
1
1
1
2
0
0
1
1
1
1
1
1
0
1
1
2
2
1
1
1
1
0
0
0
0
2
1
1
1
1
0
0
2
2
1
1
2
2
1
1
2
2
1
1
1
0
0
0
0
0
0
0
0
1
1
1
1
0
0
0
0
0
0
0
A Tiling Game






Source: Mathologer
A Tiling Game






Source: Mathologer
\(\diamond(a,b) \longrightarrow a + b \mod 3\)
\(\diamond(a,b) \longrightarrow -(a + b) \mod 3\)
A Tiling Game






Source: Mathologer
0
1
1
1
1
1
1
0
0
0
0
0
0
2
2
2
2
2
2
Double counting
\(\sum_{k=1}^n k\left(\begin{array}{l}n \\ k\end{array}\right)=n 2^{n-1}\)
Both sides count the number of ways
to choose a committee among \(n\) people,
then to choose a president from the committee.
On the left-hand side, we first choose a \(k\)-member committee in \(\left(\begin{array}{l}n \\ k\end{array}\right)\) ways, then we choose its president in \(k\) ways.
On the right-hand side, we first choose the president in \(n\) ways,
then we choose a subset of the remaining \(n-1\)-member set
of people for the role of non-president committee members in \(2^{n-1}\) ways.
Source: Bona, A Walk Through Combinatorics, Theorem 4.6
For all non-negative integers \(n\),
For all positive integers \(n, m\), and \(k\),
\(\left(\begin{array}{c}n+m \\k\end{array}\right)=\sum_{i=0}^k\left(\begin{array}{l}n \\i\end{array}\right)\left(\begin{array}{c} m \\k-i\end{array}\right) .\)
Source: Bona, A Walk Through Combinatorics, Theorem 4.7
#of ways of choosing
i objects from n
#of ways of choosing
k-i objects from m
Generating Functions
Source: 3b1b
See Also: Generating Functionology
\(c_0 x^0 + c_1 x^1 + \cdots c_k x^k + \cdots c_n x^n \)
In how many ways can we choose \(k\) objects from \(n\)?
Let \(c_k\) denote the number of ways of choosing \(k\) objects from \(n\).
\({n \choose 0} x^0 + {n \choose 1} x^1 + \cdots {n \choose k} x^k + \cdots {n \choose n} x^n \)
\(\underbrace{(1+x) \cdot (1+x) \cdot \cdots \cdot (1+x)}_{n\text{ times}}\)
\(p(x) := (1+x) \cdot (1+x^2) \cdot \cdots \cdot (1+x^n)\)
What's the largest power of \(x\) in the expansion of \(p(x)\)?
\(x^{{n+1 \choose 2}}\)
\(c_0x^0 + c_1x^1 + \cdots + c_kx^k + \cdots + c_{{n+1 \choose 2}}x^{{n+1 \choose 2}}\)
How many terms are there in the direct expansion of \(p(x)\)?
\(2^n\)
What does \(c_k\) represent?
The number of subsets of \([n]\) that add up to \(k\).
\(p(x) := (1+x) \cdot (1+x^2) \cdot \cdots \cdot (1+x^n)\)
\(= c_0x^0 + c_1x^1 + \cdots + c_kx^k + \cdots + c_{{n+1 \choose 2}}x^{{n+1 \choose 2}}\)
\(p(0) = 1 = c_0\)
\(p(1) = 2^n = \sum_{k=0}^N c_i\)
\(p(-1) = 0 = c_0 - c_1 + c_2 - \cdots \pm c_N\)
\(\equiv (c_0 + c_2 + \cdots ) = (c_1 + c_3 + \cdots )\)
\(\frac{1}{2} \left(p(1) + p(-1)\right) = 2^{n-1} = \underbrace{c_0 + c_2 + \cdots}_{\text{even terms}} \)
The # of subsets of \([n]\) whose sum is even is \(2^{n-1}\).
Find the number of subsets of {1,2,3,4,5,.. .,2000},
the sum of whose elements is divisible by 5.
Source: 3b1b
114, 813, 069, 527, 425, 452, 423, 283, 320, 117, 768, 198, 402, 231, 770, 208, 869, 520, 047, 764, 273, 682, 576, 626, 139, 237, 031, 385, 665, 948, 631, 650, 626, 991, 844, 596, 463, 898, 746, 277, 344, 711, 896, 086, 305, 533, 142, 593, 135, 616, 665, 318, 539, 129, 989, 145, 312, 280, 000, 688, 779, 148, 240, 044, 871, 428, 926, 990, 063, 486, 244, 781, 615, 463, 646, 388, 363, 947, 317, 026, 040, 466, 353, 970, 904, 996, 558, 162, 398, 808, 944, 629, 605, 623, 311, 649, 536, 164, 221, 970, 332, 681, 344, 168, 908, 984, 458, 505, 602, 379, 484, 807, 914, 058, 900, 934, 776, 500, 429, 002, 716, 706, 625, 830, 522, 008, 132, 236, 281, 291, 761, 267, 883, 317, 206, 598, 995, 396, 418, 127, 021, 779, 858, 404, 042, 159, 853, 183, 251, 540, 889, 433, 902, 091, 920, 554, 957, 783, 589, 672, 039, 160, 081, 957, 216, 630, 582, 755, 380, 425, 583, 726, 015, 528, 348, 786, 419, 432, 054, 508, 915, 275, 783, 882, 625, 175, 435, 528, 800, 822, 842, 770, 817, 965, 453, 762, 184, 851, 149, 029, 376
Conjecture: maybe one-fifth of \(2^n\)?
Verify by brute-force:
Find the number of subsets of {1,2,3,4,5},
the sum of whose elements is divisible by 5.
0, 5, 10, 15
\(\{\} \longrightarrow 0 \)
\(\{2,3\} \longrightarrow 5 \)
\(\{4,1\} \longrightarrow 5 \)
\(\{5\} \longrightarrow 5 \)
\(\{1,2,3,4,5\} \longrightarrow 15 \)
\(\{1,2,3,4\} \longrightarrow 10 \)
\(\{5,1,4\} \longrightarrow 10 \)
\(\{2,3,5\} \longrightarrow 10 \)
Check conjecture for smaller numbers?

Keep
brute-forcing...
Use
generating
functions.
\(p(x) := (1+x) \cdot (1+x^2) \cdot \cdots \cdot (1+x^n)\)
\(= c_0x^0 + c_1x^1 + \cdots + c_kx^k + \cdots + c_{{n+1 \choose 2}}x^{{n+1 \choose 2}}\)
\(p(1) = 2^n = \sum_{k=0}^N c_i\)
\(p(-1) = 0 = c_0 - c_1 + c_2 - \cdots \pm c_N\)
\(\frac{1}{2} \left(p(1) + p(-1)\right) = 2^{n-1} = \underbrace{c_0 + c_2 + \cdots}_{\text{even terms}} \)
The # of subsets of \([n]\) whose sum is even is \(2^{n-1}\).
Want to evaluate \(p(x)\) at some points
(say \(x_1, x_2, x_3, x_4, x_5\))
such that:
\(p(x_1), p(x_2), p(x_3), p(x_4), p(x_5)\) are easy to evaluate,
and
some combination of these polynomials leaves us only with the terms \(c_0, c_5, c_{10}, \ldots\) and kills everything else 🥷
\(p(x) := (1+x) \cdot (1+x^2) \cdot \cdots \cdot (1+x^n)\)
Leap of faith: let's try the fifth roots of unity.
Want to evaluate \(p(x)\) at some points
(say \(x_1, x_2, x_3, x_4, x_5\))
such that:
\(p(x_1), p(x_2), p(x_3), p(x_4), p(x_5)\) are easy to evaluate,
and
some combination of these polynomials leaves us only with the terms \(c_0, c_5, c_{10}, \ldots\) and kills everything else 🥷
\(p(x) := (1+x) \cdot (1+x^2) \cdot \cdots \cdot (1+x^n)\)
\(p(x) := (1+x) \cdot (1+x^2) \cdot \cdots \cdot (1+x^n)\)
\( = c_0x^0 + c_1x^1 + c_2x^2 + \cdots + c_Nx^N\)
Let \(\lambda_0, \lambda_1, \lambda_2, \lambda_3, \lambda_4 \) be solutions to \(z^5 = 1\).
\(\lambda = e^{\frac{2\pi i}{5}}\)
\(\lambda_0 = 1\)
\(\lambda_1 = e^{\frac{2\pi i}{5}}\)
\(\lambda_2 = e^{\frac{4\pi i}{5}}\)
\(\lambda_3 = e^{\frac{6\pi i}{5}}\)
\(\lambda_4 = e^{\frac{8\pi i}{5}}\)
\(\lambda_0 = \lambda^0\)
\(\lambda_1 = \lambda^1\)
\(\lambda_2 = \lambda^2\)
\(\lambda_3 = \lambda^3\)
\(\lambda_4 = \lambda^4\)
\(p(x) := (1+x) \cdot (1+x^2) \cdot \cdots \cdot (1+x^n)\)
\( = c_0x^0 + c_1x^1 + c_2x^2 + \cdots + c_Nx^N\)
Let \(\lambda^0, \lambda^1, \lambda^2, \lambda^3, \lambda^4 \) be solutions to \(z^5 = 1\).
\(\lambda = e^{\frac{2\pi i}{5}}\)
\(p(\lambda^0) + p(\lambda^1) + p(\lambda^2) + p(\lambda^3) + p(\lambda^4)\)
\(\begin{aligned} = & ~~c_0({\color{indianred}\lambda^0})^0\\ +& ~~c_1({\color{indianred}\lambda^0})^1\\ +& ~~c_2({\color{indianred}\lambda^0})^2 \\+&~~ \vdots \end{aligned}\)
\(\begin{aligned} + & ~~c_0({\color{indianred}\lambda^1})^0\\ +& ~~c_1({\color{indianred}\lambda^1})^1\\ +& ~~c_2({\color{indianred}\lambda^1})^2 \\+&~~ \vdots \end{aligned}\)
\(\begin{aligned} + & ~~c_0({\color{indianred}\lambda^2})^0\\ +& ~~c_1({\color{indianred}\lambda^2})^1\\ +& ~~c_2({\color{indianred}\lambda^2})^2 \\+&~~ \vdots \end{aligned}\)
\(\begin{aligned} + & ~~c_0({\color{indianred}\lambda^3})^0\\ +& ~~c_1({\color{indianred}\lambda^3})^1\\ +& ~~c_2({\color{indianred}\lambda^3})^2 \\+&~~ \vdots \end{aligned}\)
\(\begin{aligned} + & ~~c_0({\color{indianred}\lambda^4})^0\\ +& ~~c_1({\color{indianred}\lambda^4})^1\\ +& ~~c_2({\color{indianred}\lambda^4})^2 \\+&~~ \vdots \end{aligned}\)
\(p(x) := (1+x) \cdot (1+x^2) \cdot \cdots \cdot (1+x^n)\)
\( = c_0x^0 + c_1x^1 + c_2x^2 + \cdots + c_Nx^N\)
Let \(\lambda^0, \lambda^1, \lambda^2, \lambda^3, \lambda^4 \) be solutions to \(z^5 = 1\).
\(\lambda = e^{\frac{2\pi i}{5}}\)
\(p(\lambda^0) + p(\lambda^1) + p(\lambda^2) + p(\lambda^3) + p(\lambda^4)\)
\(\begin{aligned} = & ~~c_0\{({\color{indianred}\lambda^0})^0 + ({\color{indianred}\lambda^1})^0 + ({\color{indianred}\lambda^2})^0 + ({\color{indianred}\lambda^3})^0 + ({\color{indianred}\lambda^4})^0\}\\ + & ~~c_1\{({\color{indianred}\lambda^0})^1 + ({\color{indianred}\lambda^1})^1 + ({\color{indianred}\lambda^2})^1 + ({\color{indianred}\lambda^3})^1 + ({\color{indianred}\lambda^4})^1\}\\ + & ~~c_2\{({\color{indianred}\lambda^0})^2 + ({\color{indianred}\lambda^1})^2 + ({\color{indianred}\lambda^2})^2 + ({\color{indianred}\lambda^3})^2 + ({\color{indianred}\lambda^4})^2\}\\ + & ~~c_3\{({\color{indianred}\lambda^0})^3 + ({\color{indianred}\lambda^1})^3 + ({\color{indianred}\lambda^2})^3 + ({\color{indianred}\lambda^3})^3 + ({\color{indianred}\lambda^4})^3\}\\ + & ~~c_4\{({\color{indianred}\lambda^0})^4 + ({\color{indianred}\lambda^1})^4 + ({\color{indianred}\lambda^2})^4 + ({\color{indianred}\lambda^3})^4 + ({\color{indianred}\lambda^4})^4\}\\ + & ~~c_5\{({\color{indianred}\lambda^0})^5 + ({\color{indianred}\lambda^1})^5 + ({\color{indianred}\lambda^2})^5 + ({\color{indianred}\lambda^3})^5 + ({\color{indianred}\lambda^4})^5\}\\ +&~~ \vdots \end{aligned}\)
\(p(x) := (1+x) \cdot (1+x^2) \cdot \cdots \cdot (1+x^n)\)
\( = c_0x^0 + c_1x^1 + c_2x^2 + \cdots + c_Nx^N\)
Let \(\lambda^0, \lambda^1, \lambda^2, \lambda^3, \lambda^4 \) be solutions to \(z^5 = 1\).
\(\lambda = e^{\frac{2\pi i}{5}}\)
\(p(\lambda^0) + p(\lambda^1) + p(\lambda^2) + p(\lambda^3) + p(\lambda^4)\)
\(\begin{aligned} = & ~~c_0\{({\color{indianred}\lambda^{0}}) + ({\color{indianred}\lambda^{0}}) + ({\color{indianred}\lambda^{0}}) + ({\color{indianred}\lambda^{0}}) + ({\color{indianred}\lambda^{0}})\}\\ + & ~~c_1\{({\color{indianred}\lambda^{0}}) + ({\color{indianred}\lambda^{1}}) + ({\color{indianred}\lambda^{2}}) + ({\color{indianred}\lambda^{3}}) + ({\color{indianred}\lambda^{4}})\}\\ + & ~~c_2\{({\color{indianred}\lambda^{0}}) + ({\color{indianred}\lambda^{2}}) + ({\color{indianred}\lambda^{4}}) + ({\color{indianred}\lambda^{6}}) + ({\color{indianred}\lambda^{8}})\}\\ + & ~~c_3\{({\color{indianred}\lambda^{0}}) + ({\color{indianred}\lambda^{3}}) + ({\color{indianred}\lambda^{6}}) + ({\color{indianred}\lambda^{9}}) + ({\color{indianred}\lambda^{12}})\}\\ + & ~~c_4\{({\color{indianred}\lambda^{0}}) + ({\color{indianred}\lambda^{4}}) + ({\color{indianred}\lambda^{8}}) + ({\color{indianred}\lambda^{12}}) + ({\color{indianred}\lambda^{16}})\}\\ + & ~~c_5\{({\color{indianred}\lambda^{0}}) + ({\color{indianred}\lambda^{5}}) + ({\color{indianred}\lambda^{10}}) + ({\color{indianred}\lambda^{15}}) + ({\color{indianred}\lambda^{20}})\}\\ +&~~ \vdots \end{aligned}\)
\(p(x) := (1+x) \cdot (1+x^2) \cdot \cdots \cdot (1+x^n)\)
\( = c_0x^0 + c_1x^1 + c_2x^2 + \cdots + c_Nx^N\)
Let \(\lambda^0, \lambda^1, \lambda^2, \lambda^3, \lambda^4 \) be solutions to \(z^5 = 1\).
\(\lambda = e^{\frac{2\pi i}{5}}\)
\(p(\lambda^0) + p(\lambda^1) + p(\lambda^2) + p(\lambda^3) + p(\lambda^4)\)
\(\begin{aligned} = & ~~c_0\{({\color{indianred}\lambda^{0}}) + ({\color{indianred}\lambda^{0}}) + ({\color{indianred}\lambda^{0}}) + ({\color{indianred}\lambda^{0}}) + ({\color{indianred}\lambda^{0}})\}\\ + & ~~c_1\{({\color{indianred}\lambda^{0}}) + ({\color{indianred}\lambda^{1}}) + ({\color{indianred}\lambda^{2}}) + ({\color{indianred}\lambda^{3}}) + ({\color{indianred}\lambda^{4}})\}\\ + & ~~c_2\{({\color{indianred}\lambda^{0}}) + ({\color{indianred}\lambda^{2}}) + ({\color{indianred}\lambda^{4}}) + ({\color{indianred}\lambda^{1}}) + ({\color{indianred}\lambda^{3}})\}\\ + & ~~c_3\{({\color{indianred}\lambda^{0}}) + ({\color{indianred}\lambda^{3}}) + ({\color{indianred}\lambda^{1}}) + ({\color{indianred}\lambda^{4}}) + ({\color{indianred}\lambda^{2}})\}\\ + & ~~c_4\{({\color{indianred}\lambda^{0}}) + ({\color{indianred}\lambda^{4}}) + ({\color{indianred}\lambda^{3}}) + ({\color{indianred}\lambda^{2}}) + ({\color{indianred}\lambda^{1}})\}\\ + & ~~c_5\{({\color{indianred}\lambda^{0}}) + ({\color{indianred}\lambda^{0}}) + ({\color{indianred}\lambda^{0}}) + ({\color{indianred}\lambda^{0}}) + ({\color{indianred}\lambda^{0}})\}\\ +&~~ \vdots \end{aligned}\)
\(p(x) := (1+x) \cdot (1+x^2) \cdot \cdots \cdot (1+x^n)\)
\( = c_0x^0 + c_1x^1 + c_2x^2 + \cdots + c_Nx^N\)
Let \(\lambda^0, \lambda^1, \lambda^2, \lambda^3, \lambda^4 \) be solutions to \(z^5 = 1\).
\(\lambda = e^{\frac{2\pi i}{5}}\)
\(p(\lambda^0) + p(\lambda^1) + p(\lambda^2) + p(\lambda^3) + p(\lambda^4)\)
= \(5 \cdot (c_0 + c_5 + c_{10} + \cdots) \)
All that remains is to compute:
\(p(\lambda^0), p(\lambda^1), p(\lambda^2), p(\lambda^3), p(\lambda^4)\).
\(p(x) := (1+x) \cdot (1+x^2) \cdot \cdots \cdot (1+x^n)\)
Let \(\lambda^0, \lambda^1, \lambda^2, \lambda^3, \lambda^4 \) be solutions to \(z^5 = 1\).
\(\lambda = e^{\frac{2\pi i}{5}}\)
\(p(\lambda^0) + p(\lambda^1) + p(\lambda^2) + p(\lambda^3) + p(\lambda^4)\)
= \(5 \cdot (c_0 + c_5 + c_{10} + \cdots) \)
The lambdas are solutions to \(z^5 = 1\).
\(\equiv\) The lambdas are solutions to \(z^5 - 1 = 0\).
\(z^5 -1 = (z - \lambda^0) (z - \lambda^1) (z - \lambda^2) (z - \lambda^3) (z - \lambda^4)\)
Current goal: compute \(p(\lambda^0), p(\lambda^1), p(\lambda^2), p(\lambda^3), p(\lambda^4)\).
\((-1)^5 -1 = (-1 - \lambda^0) (-1 - \lambda^1) (-1 - \lambda^2) (-1 - \lambda^3) (-1 - \lambda^4)\)
\(p(\lambda) := \{(1+\lambda) (1+\lambda^2) (1+\lambda^3) (1+ \lambda^4) (1+\lambda^0)\}^{\ell}; \text{ where } n = 5\ell.\)
Let \(\lambda^0, \lambda^1, \lambda^2, \lambda^3, \lambda^4 \) be solutions to \(z^5 = 1\).
\(\lambda = e^{\frac{2\pi i}{5}}\)
\(p(\lambda^0) + p(\lambda^1) + p(\lambda^2) + p(\lambda^3) + p(\lambda^4)\)
= \(5 \cdot (c_0 + c_5 + c_{10} + \cdots) \)
\(z^5 -1 = (z - \lambda^0) (z - \lambda^1) (z - \lambda^2) (z - \lambda^3) (z - \lambda^4)\)
Current goal: compute \(p(\lambda^0), p(\lambda^1), p(\lambda^2), p(\lambda^3), p(\lambda^4)\).
\(2 = (1 + \lambda^0) (1 + \lambda^1) (1 + \lambda^2) (1 + \lambda^3) (1 + \lambda^4)\)
\(\equiv\) The lambdas are solutions to \(z^5 - 1 = 0\).
\(p(\lambda) := \{(1+\lambda) (1+\lambda^2) (1+\lambda^3) (1+ \lambda^4) (1+\lambda^0)\}^{\ell}; \text{ where } n = 5\ell.\)
Let \(\lambda^0, \lambda^1, \lambda^2, \lambda^3, \lambda^4 \) be solutions to \(z^5 = 1\).
\(\lambda = e^{\frac{2\pi i}{5}}\)
\(p(\lambda^0) + p(\lambda^1) + p(\lambda^2) + p(\lambda^3) + p(\lambda^4)\)
= \(5 \cdot (c_0 + c_5 + c_{10} + \cdots) \)
\(z^5 -1 = (z - \lambda^0) (z - \lambda^1) (z - \lambda^2) (z - \lambda^3) (z - \lambda^4)\)
Current goal: compute \(p(\lambda^0), p(\lambda^1), p(\lambda^2), p(\lambda^3), p(\lambda^4)\).
\(2 = (1 + \lambda^0) (1 + \lambda^1) (1 + \lambda^2) (1 + \lambda^3) (1 + \lambda^4)\)
\(\equiv\) The lambdas are solutions to \(z^5 - 1 = 0\).
\(p(\lambda) := 2^{\ell}; \text{ where } n = 5\ell.\)
\(c_0 + c_5 + c_{10} + \cdots\)
= \(\frac{2^{n} + 4\cdot 2^{\ell}}{5}\)
= \(5 \cdot (c_0 + c_5 + c_{10} + \cdots) \)
\(2^n + 2^\ell + 2^\ell + 2^\ell +2^\ell\)
Discrete > CONTINUOUS
...and back
Sources: 3b1b, Numberphile
The Stolen Necklace Problem
Given: a stolen necklace with two kinds of beads
(\(p = 2k\) rubies and \(q = 2\ell\) diamonds);
& two thieves.
Goal. Cut the necklace into as few pieces as possible
so that the pieces can be distributed between the two thieves
in such a way that
the bead types are equally distributed.
The Stolen Necklace Problem
Given: a stolen necklace with two kinds of beads
(\(p = 2k\) rubies and \(q = 2\ell\) diamonds);
& two thieves.
Goal. Cut the necklace into as few pieces as possible
so that the pieces can be distributed between the two thieves
in such a way that
the bead types are equally distributed.
Two cuts are (sometimes) necessary.
\(\underbrace{~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~}_{p=2k\text{ diamonds}}\)
\(\underbrace{~~~~~~~~~~~~~~~~~~~~~~~~~}_{q=2\ell\text{ rubies}}\)
Two cuts are (always) enough.
Too few (\(< \ell\)) rubies
Too many (\(> \ell\)) rubies
Two cuts are (always) enough.
Two cuts are (always) enough.
Net Change in #rubies = 0
Two cuts are (always) enough.
Net Change in #rubies = 0
Two cuts are (always) enough.
Net Change in #rubies = -1
Two cuts are (always) enough.
Net Change in #rubies = +1
Two cuts are (always) enough.
Two cuts are (always) enough.
Two cuts are (always) enough.
Two cuts are (always) enough.
Too few (\(< \ell\)) rubies
Too many (\(> \ell\)) rubies
Two cuts are (always) enough.
Next up: an alternate proof that scales up to the case of more jewel types and/or more thieves.
Main Ideas
1. Map the discrete necklace to the unit interval, with each bead mapped to a \(1/(2k+2l)\)-length subinterval colored with the color of the bead.
2. Observe that any two cuts on the interval that correspond to a equitable division in terms of distributing blue and red lengths can be pulled back to two cuts of the necklace that can be equitably distributed.
3. Create a bijection between points on a sphere &
(cuts + allocation) of the interval.
4. Define an appropriate function from the sphere to \(\mathbb{R}^2\) and invoke a result about antipodal points to recover a good cut on the intervals, and use fact #2 to pull back to the necklace.
Total length of blue intervals = \(\frac{2k}{(2k + 2\ell)}\) = \(\frac{k}{(k + \ell)}\)
Total length of red intervals = \(\frac{2\ell}{(2k + 2\ell)}\) = \(\frac{\ell}{(k + \ell)}\)
Find two cuts anywhere such that at least one piece has:
Total length of blue intervals = \(\frac{k}{(2k + 2\ell)}\) = \(\frac{1}{2} \frac{k}{(k + \ell)}\)
Total length of red intervals = \(\frac{\ell}{(2k + 2\ell)}\) = \(\frac{1}{2} \frac{\ell}{(k + \ell)}\)
If \(f: S^2 \rightarrow \mathbb{R}^2\) is continuous
then there exists an \(x \in S^2\) such that:
\({\color{indianred}f(−x)=f(x)}\).
...at any moment, there is always a pair of antipodal points on the Earth's surface with equal temperatures and equal barometric pressures, assuming that both parameters vary continuously in space.
Find two cuts anywhere such that at least one piece has:
Total length of blue intervals = \(k\)
Total length of red intervals = \(\ell\)
\(x^2 + y^2 + z^2 = 1\)

The point \((x,y,z)\) satisfies
Pick cuts so that:
the first interval has length \(x^2\),
the second interval has length \(y^2\), and
the third interval has length \(z^2\).
If \(x > 0\) give the first interval to the first thief; otherwise give it to the second thief.
\(x^2 + y^2 + z^2 = 1\)

The point \((x,y,z)\) satisfies
Pick cuts so that:
the first interval has length \(x^2\),
the second interval has length \(y^2\), and
the third interval has length \(z^2\).
If \(y > 0\) give the second interval to the first thief; otherwise give it to the second thief.
If \(z > 0\) give the third interval to the first thief; otherwise give it to the second thief.
\(f(x,y,z) \rightarrow ({\color{dodgerblue}\alpha},{\color{indianred}\beta})\)
\(\alpha\) is the total length of the blue intervals received by the first thief under the cut corresponding to \(x,y,z\).
\(\beta\) is the total length of the red intervals received by the first thief under the cut corresponding to \(x,y,z\).
\(\exists (x,y,z)\) such that:
\(\underbrace{f(x,y,z) = f(-x,-y,-z)}_{\text{...by B-U theorem.}}\)
If \(f: S^n \rightarrow \mathbb{R}^n\) is continuous
then there exists an \(x \in S^n\) such that:
\({\color{indianred}f(−x)=f(x)}\).
...use this if you have necklaces with more bead types!
Discrete mathematics
Exam 1 Instructions
Please ensure you have 2 sheets - Part 1 and Part 2.
All problems in Part 1 (except problem 4) carry
1 mark for a correct answer & a -0.5 penalty for an incorrect answer.
OPEN: notes and textbooks. NOT ALLOWED: devices, internet, discussions.
Remember to write your roll number and name on both sheets.
Problems in Part 2 are 4 points each.
Each part of problem 4 carries
2 marks for a correct answer & a -1 penalty for an incorrect answer.
Problem 7. All polynomials considered have finite degree.
Problem 10. Read "her" as "his".
Problem 11. Read "10 lakh rupees" as "1 million dollars".
Note that the question is to maximize the amount the leader can pocket.
WRITE YOUR ANSWERS WITHIN THE SPACE GIVEN.
Please ensure you have 2 sheets - Part 1 and Part 2.
All problems in Part 1 carry
1 mark for a correct answer & a -0.5 penalty for an incorrect answer.
OPEN: notes and textbooks. NOT ALLOWED: devices, internet, discussions.
Remember to write your roll number and name on both sheets.
Problem 2. Read "intersect at a vertex" as
"intersect at at least one vertex".
WRITE YOUR ANSWERS WITHIN THE SPACE GIVEN.
Problem 5. Assume the vertices are labeled \(1\) to \(n\).
Discrete mathematics
Slides ⋅ Week 06 ⋅ 12th and 13th September, 2023
The Geography Game
Played on a simple, undirected graph \(G\)
with a token on some vertex.
Two players: red (R) and blue (B).
Turn-based.
On your turn, move the token to an adjacent unmarked vertex and mark the vertex that you move to.
To begin with, the token is at a designated marked vertex \(v\), & this is the only marked vertex in the graph.
The Geography Game
Hint. Recall the dominoes/chessboard game
from the first quiz.
Theorem. Let \(G\) be a graph and \(v\) a vertex of \(G\).
Then the geography game starting at \((G, v)\) is a first player win if and only if _________________.
Definition. A matching is a collection of vertex-disjoint edges.
In other words, a matching \(M\) in a graph \(G = (V,E)\)
is a subset of \(E\) such that
any pair of edges \(e,f \in M\) do not share an endpoint.
If \(M = \{e_1 = (u_1,v_1), \cdots, e_k = (u_k,v_k)\}\) is matching,
then \(u_i \neq u_j, v_i \neq v_j, u_i \neq v_j\), for all \(1 \leq i \neq j \leq k\);
and in a simple graph, \(u_i \neq v_i\) for all \(1 \leq i \leq k\).
A matching on \(k\) edges involves (saturates) \(2k\) vertices.
A matching on \(k\) is said to have size \(k\).
A maximal matching is a matching M of a graph G that is not a proper subset of any other matching.
A maximum matching is a matching that contains the largest possible number of edges.
Every maximum matching is maximal,
but not every maximal matching is a maximum matching.
The Geography Game
Theorem. Let \(G\) be a graph and \(v\) a vertex of \(G\).
Then the geography game starting at \((G, v)\) is a first player win if and only if _________________.
The Geography Game
Theorem. Let \(G\) be a graph and \(v\) a vertex of \(G\).
Then the geography game starting at \((G, v)\) is a first player win if and only if every maximum matching of \(G\) saturates \(v\).
The Geography Game
Theorem (only if). Let \(G\) be a graph and \(v\) a vertex of \(G\).
If there exists a maximum matching of \(G\) does not saturate \(v\), then the second player wins.
\(v\)
a matching \(M\) that does not saturate \(v\).
\(v\)
a matching \(M\) that does not saturate \(v\).
The first player
is forced to bounce back inside the matching \(M\).
The second player
can keep playing along edges of \(M\),
and is never out of moves.
The Geography Game
Theorem (if). Let \(G\) be a graph and \(v\) a vertex of \(G\).
If every maximum matching of \(G\) saturates \(v\), then
the first player wins.
\(v\)
a maximum matching \(M\) that saturates \(v\).
& the knowledge that every maximum matching saturates \(v\).
\(v\)
a maximum matching \(M\) that saturates \(v\).
& the knowledge that every maximum matching saturates \(v\).
\(v\)
a maximum matching \(M\) that saturates \(v\).
& the knowledge that every maximum matching saturates \(v\).
\(v\)
a maximum matching \(M\) that saturates \(v\).
& the knowledge that every maximum matching saturates \(v\).
\(v\)
a maximum matching \(M\) that saturates \(v\).
& the knowledge that every maximum matching saturates \(v\).
\(v\)
a maximum matching \(M\) that saturates \(v\).
& the knowledge that every maximum matching saturates \(v\).
\(v\)
a maximum matching \(M\) that saturates \(v\).
& the knowledge that every maximum matching saturates \(v\).
If the second player can venture
outside of \(M\),
then by swapping the edges of the first player moves and the second player moves,
we get a maximum matching
that does not saturate \(v\),
a contradiction.
A bipartite graph is a graph whose vertices can be
divided into two disjoint sets \(A\) and \(B\) such that
every edge connects a vertex in \(A\) to one in \(B\).
When does a bipartite graph have a perfect matching?
a
b
c
d
e
p
q
r
s
t
When does a bipartite graph have a perfect matching?
a
b
c
d
e
p
q
r
s
t
Does this graph have a perfect matching?
a
b
c
d
e
p
q
r
s
t
No, because there is a congestion:
a
b
c
d
e
p
q
r
s
t
Cool Theorem. A bipartite graph \(G = (V = (A \uplus B), E)\) with \(|A| = |B| = n\) vertices has a perfect matching if and only if there is no congestion.
a
b
c
d
e
p
q
r
s
t
An Application.
Definition. A doubly stochastic matrix is one in which every row and column consists of non-negative reals adding to one.
A permutation matrix is a doubly stochastic matrix with entries in \(\{0,1\}\).
The Birkhoff-von Neumann Theorem
Theorem. If \(X\) is a doubly stochastic matrix,
then there exist \(\theta_1, \ldots, \theta_k \geqslant 0, \sum_{i=1}^k \theta_i=1\)
& permutation matrices \(P_1, \ldots, P_k\)such that
\(X=\theta_1 P_1+\cdots+\theta_k P_k.\)
(Such a decomposition of \(X\) is known as a convex combination.)
For instance if \(X=\frac{1}{12}\left(\begin{array}{lll}7 & 0 & 5 \\ 2 & 6 & 4 \\ 3 & 6 & 3\end{array}\right)\) then:
\(P=\left(\begin{array}{lll}0 & 0 & 1 \\ 1 & 0 & 0 \\ 0 & 1 & 0\end{array}\right), \lambda=\frac{2}{12}\), and \(X-\lambda P=\frac{1}{12}\left(\begin{array}{ccc}7 & 0 & 3 \\ 0 & 6 & 4 \\ 3 & 4 & 3\end{array}\right)\).
The plan: we will show that there exists a permutation matrix \(P\) such that:
\(x_{ij} \neq 0\) whenever \(p_{ij} \neq 0\).
Thus if we let \(\lambda\) be the smallest \(x_{ij}\) corresponding to a non-zero \(p_{ij}\), the difference \(X-\lambda P \)
will be a scalar multiple of a doubly stochastic matrix and
will have at least one more zero cell than X.
Every row is a vertex in \(A\).
Every column is a vertex in \(B\).
There is an edge between \(u \in A\) and \(v \in B\)
if \(x_{uv} \neq 0\).
Want to show:
This graph has a perfect matching.
Matrix → Graph
extras
(Slides)
Discrete mathematics
Slides ⋅ Week 07 ⋅ 19th and 20th September, 2023
19th September: The Math of Juggling
(Guest Lecture by Prof. Bireswar Das)
Please find the slides for this session
in Google Classroom.
(Hall's Theorem.) A bipartite graph \(G = ((A \uplus B),E)\) has a perfect matching if and only if
for every subset \(S \subseteq A\) we have that:
\(|N(S)| \geqslant |S|.\)
(Hall's Theorem.) A bipartite graph \(G = ((A \uplus B),E)\) has a perfect matching if and only if
for every subset \(S \subseteq A\) we have that:
\(|N(S)| \geqslant |S|.\)
(Hall's Theorem.) A bipartite graph \(G = ((A \uplus B),E)\) has a perfect matching if and only if
for every subset \(S \subseteq A\) we have that:
\(|N(S)| \geqslant |S|.\)
(Hall's Theorem.) A bipartite graph \(G = ((A \uplus B),E)\) has a perfect matching if and only if
for every subset \(S \subseteq A\) we have that:
\(|N(S)| \geqslant |S|.\)
(Hall's Theorem.) A bipartite graph \(G = ((A \uplus B),E)\) has a perfect matching if and only if
for every subset \(S \subseteq A\) we have that:
\(|N(S)| \geqslant |S|.\)
\(|{\color{IndianRed}S}| + |N({\color{DodgerBlue}T})| = |N({\color{IndianRed}S})| + |N({\color{DodgerBlue}T})| \geqslant |N({\color{IndianRed}S} \cup {\color{DodgerBlue}T})| \geqslant |{\color{IndianRed}S} \cup {\color{DodgerBlue}T}| = |{\color{IndianRed}S}| + |{\color{DodgerBlue}T}|\)
(Hall's Theorem.) A bipartite graph \(G = ((A \uplus B),E)\) has a perfect matching if and only if
for every subset \(S \subseteq A\) we have that:
\(|N(S)| \geqslant |S|.\)
\(|{\color{IndianRed}S}| + |N({\color{DodgerBlue}T})| = |N({\color{IndianRed}S})| + |N({\color{DodgerBlue}T})| \geqslant |N({\color{IndianRed}S} \cup {\color{DodgerBlue}T})| \geqslant |{\color{IndianRed}S} \cup {\color{DodgerBlue}T}| = |{\color{IndianRed}S}| + |{\color{DodgerBlue}T}|\)
Graph Coloring
Graph Coloring
Graph Coloring
Graph Coloring
Graph Coloring
Graph Coloring
Goal.
Color the vertices of a graph
so that any pair of adjacent vertices
are colored with distinct colors.
Chromatic Number.
The smallest number of colors
with which such a coloring is possible.
Graph Coloring
Greedy Coloring.
Palette: {1,2,3,...}
Color every vertex with the
smallest color that does not cause a conflict.
Graph Coloring
Graph Coloring
Graph Coloring
Graph Coloring
Graph Coloring
Graph Coloring
Graph Coloring
Graph Coloring
Graph Coloring
Graph Coloring
Graph Coloring
Graph Coloring
Graph Coloring
Graph Coloring
Graph Coloring
Graph Coloring
Graph Coloring
Graph Coloring
Graph Coloring
Greedy Algorithm.
Every graph can be colored with at most \(\Delta(G) + 1\) colors.
Brook's Theorem.
In a connected graph in which every vertex has at most Δ neighbors,
the vertices can be colored with only Δ colors,
except for two cases:
complete graphs & odd-length cycles,
which require Δ + 1 colors.
Are there graphs that need \(\Delta(G) + 1\) many colors?
Graph Coloring
Four Color Theorem.
The chromatic number of a planar graph is no greater than four.
In 1976, Appel and Haken caused delight mixed with consternation by proving the celebrated four colour theorem, but with heavy reliance on a computer calculation. An assembly language program was used to check 1936 “reducible configurations”; people were rightly concerned about errors in the code.
However, the Appel–Haken proof also required “the investigation by hand about ten thousand neighbourhoods of countries with positive charge”,
much of which was done by Appel’s 13-year-old daughter,
and nobody seemed bothered about the possibility of errors there.
Computer algebra systems were emerging around that time and would eventually become widely used in many branches of science and engineering, although I can’t imagine a computer algebra calculation being uncritically accepted by any mathematics journal.
[Source]
Graph Coloring
Four Color Theorem.
The chromatic number of a planar graph is no greater than four.
Five Color Theorem.
The chromatic number of a planar graph is no greater than five.
planar graphs
A graph is called planar if it can be drawn in the plane without any edges crossing (where a crossing of edges is the intersection of the lines or ares representing them at a point other than their common endpoint).
Such a drawing is called a planar representation of the graph.
Play planarity!
planar graphs
Euler's Formula. Let \(G\) be a connected planar simple graph
with \(E\) edges and \(V\) vertices.
Let \(R\) be the number of regions in a planar representation of \(G\).
Then \(R=E-V+2\).
Proof of Euler's Formula
First, we specify a planar representation of \(G\).
We will prove the theorem by constructing a sequence of subgraphs \(G_1, G_2, \ldots, G_c=G\), successively adding an edge at each stage.
Arbitrarily pick one edge of \(G\) to obtain \(G_1\).
Obtain \(G_n\) from \(G_{n-1}\) by arbitrarily adding an edge that is incident with a vertex already in \(G_{n-1}\), adding the other vertex incident with this edge if it is not already in \(G_{n-1}\).
This construction is possible because \(G\) is connected.
Proof of Euler's Formula
\(G\) is obtained after \(e\) edges are added.
Let \(r_n, e_n\), and \(v_n\) represent the number of regions, edges, and vertices
of the planar representation of \(G_n\)
induced by the planar representation of \(G\), respectively.
The proof will now proceed by induction.
Proof of Euler's Formula
The relationship \(r_1=e_1-v_1+2\) is true for \(G_1\), because \(e_1=1, v_1=2\), and \(r_1=1\).
Assume that \(r_k=e_k-v_k+2\).
Let \(\left\{a_{k+1}, b_{k+1}\right\}\) be the edge that is added to \(G_k\)
to obtain \(G_{k+1}\).
BASE CASE
Induction Hypothesis
Induction STEP
Proof of Euler's Formula
There are two possibilities to consider.
In the first case, both \(a_{k+1}\) and \(b_{k+1}\) are already in \(G_k\).
In the second case, one of the two vertices of the new edge is not already in \(G_k\).
\(r_k=e_k-v_k+2\).
Proof of Euler's Formula
Note: in case (a), these two vertices must be on the boundary of a common region \(R\), or else it would be impossible to add the edge \(\left\{a_{k+1}, b_{k+1}\right\}\) to \(G_k\) without two edges crossing (and \(G_{k+1}\) is planar).

\(r_k=e_k-v_k+2\).
planar graphs
A walk is a sequence of edges
\(e_1, \ldots, e_{n-1}\)
such that there exists a sequence of vertices
\(v_1, \ldots, v_n\)
for which \(e_i = (v_i, v_{i+1})\)
for all \(1 \leqslant i \leqslant n-1\).
Definitions
A path is a sequence of edges
\(e_1, \ldots, e_{n-1}\)
such that there exists a sequence of vertices
\(v_1, \ldots, v_n\)
for which \(e_i = (v_i, v_{i+1})\)
for all \(1 \leqslant i \leqslant n-1\),
where all vertices are distinct.
Definitions
A cycle is a sequence of edges
\(e_1, \ldots, e_{n-1}\)
such that there exists a sequence of vertices
\(v_1, \ldots, v_n\)
for which \(e_i = (v_i, v_{i+1})\)
for all \(1 \leqslant i \leqslant n-1\),
where all vertices are distinct except \(v_n = v_1\).
Definitions
A spanning tree is a subset of edges
\(e_1, \ldots, e_{n-1}\)
such that the subgraph induced by just these edges is
(a) connected
(b) acyclic
In other words, a spanning tree is
a minimally connected subgraph.
Definitions
Definitions
Definitions
not a spanning tree because the
graph induced by the edges is not connected
Definitions
not a spanning tree because the
graph induced by the edges has a cycle
Definitions
Definitions
#edges in a spanning tree = #vertices - 1
Definitions
#edges in a spanning tree = #vertices - 1
Claim: every tree on at least two vertices has at least two leaves (i.e, vertices of degree one).
Proof (idea). Let \(P\) be a maximal path. Let the endpoints of \(P\) be \(u\) and \(v\).
Note that \(u\) and \(v\) have degree at least one, since they have a neighbor on the path.
Further, they have degree at most one because they cannot have any additional neighbors on the path (this would lead to cycles), or off it (this would contradict the maximality of \(P\)).
Definitions
#edges in a spanning tree = #vertices - 1
Induction hypothesis: every tree on n vertices has \(n-1\) edges.
Induction Step (idea).
Let \(T\) be a tree on \(n+1\) vertices,
and let \(v\) be a leaf in \(T\).
Apply the induction hypothesis to \(T \setminus \{v\}\) to see that \(T\) has \(n\) edges.
(Note that \(T \setminus \{v\}\) is a tree.)
Definitions
The dual of a planar graph:
\(V(D_G) = \text{regions}(G)\)
\(E(D_G) := \{(v_p,v_q)~|~\text{ if } p,q \text{ shared an edge in } G\}\)
Definitions
Definitions
Definitions
Regions cut out by original graph <> Vertices of dual graph
Edges of original graph <> Edges of dual graph
Cycles of original graph <> Connected zones of dual graph
Connected zones of original graph <> Cycles of dual graph
Spanning tree in original graph <> Complement of spanning tree in dual graph
original graph <> Dual of dual graph
\(\underbrace{V - 1}_{\text{spanning tree in }G}\) + \(\underbrace{R - 1}_{\text{spanning tree in }D_G}\) = \(\underbrace{E(G)}_{\text{all edges}}\)
\(V + R - E = 2\)
Euler's Formula
Euler's Formula: Consequences
If G is a connected planar simple graph with \(e\) edges and \(v\) vertices, where \(v \geqslant 3\), then
\(e \leqslant 3v - 6\).
\(2e = \sum_{r \in R} \text{deg}(r) \geqslant 3r \)
\((2/3)e \geqslant r = (e - v + 2)\)
\(v-2 \geqslant (e/3)\)
Euler's Formula: Consequences
If \(G\) is a connected planar simple graph,
then \(G\) has a vertex of degree not exceeding five.
\(e \leqslant 3v - 6\)
\(\sum_{v \in V} d(v) = 2e \leqslant 6v - 12\)
If every vertex had degree \(\geqslant 6\) then
the LHS would be \(\geqslant 6v\); a contradiction.
Graph Coloring
Four Color Theorem.
The chromatic number of a planar graph is no greater than four.
Five Color Theorem.
The chromatic number of a planar graph is no greater than five.
Please stay back after the quiz for a hands-on interactive session with our friends from the
Center for Creative Learning :)
Discrete mathematics
Slides ⋅ Week 08 ⋅ 26th and 27th September, 2023
One final game.
Discrete Math
By Neeldhara Misra
Discrete Math
- 4,023



