Constraint Satisfaction
Problems
Propositional Logic
ft. The Black Vienna Game
27 suspects, whose names are A,B,C,...,Z,Ö.
Ingredients
3 criminals, sometimes referred to as the Black Vienna ring. This is an unknown three-sized subset of A,B,C,...,Z,Ö.
3 investigators, who separately have alibis for 8 suspects each. These eight-sized subsets are disjoint from each other.
The game progresses in a sequence of queries.
You are dealt three sets containing three suspects each.
Ingredients
You can choose any of these available sets, and pick an investigator (red, blue, or green) and ask them to tell you how many (not which!) of the three suspects they have alibis for.
So they can certify how many people from the given three
are NOT in the gang: 0, 1, 2, or 3.
Propositional Logic
ft. The Black Vienna Game
Propositional Logic
ft. The Black Vienna Game
Propositional Logic
ft. The Black Vienna Game
Let's play:
Propositional Logic
Proposition. A proposition is a declarative sentence (that is, a sentence that declares a fact) that is either true or false, but not both.
We use letters to denote propositional variables.
The conventional letters used for propositional variables are p, q, r, s, ...
U belongs to the BV ring.
The truth value of a proposition is true (T) if it is a true proposition.
The truth value of a proposition is false (F), if it is a false proposition.
Propositions that cannot be expressed in terms of simpler propositions are called atomic propositions.
Propositional Logic

Propositional Logic
p
q
p 🤝 q
T
T
T
T
F
F
F
F
*
*
*
*
There are 16 truth tables.
Expressing BV with Propositional Logic
\(p_A := \) A belongs to the blue team.
\(p_B := \) B belongs to the blue team.
\(p_C := \) C belongs to the blue team.
\(\vdots\)
\(p_Z := \) Z belongs to the blue team.
Expressing BV with Propositional Logic
\(q_A := \) A belongs to the red team.
\(q_B := \) B belongs to the red team.
\(q_C := \) C belongs to the red team.
\(\vdots\)
\(q_Z := \) Z belongs to the red team.
Expressing BV with Propositional Logic
\(r_A := \) A belongs to the green team.
\(r_B := \) B belongs to the green team.
\(r_C := \) C belongs to the green team.
\(\vdots\)
\(r_Z := \) Z belongs to the green team.
Expressing BV with Propositional Logic
\(r_A := \) A belongs to the green team.
\(r_B := \) B belongs to the green team.
\(r_C := \) C belongs to the green team.
\(\vdots\)
\(r_Z := \) Z belongs to the green team.
Expressing BV with Propositional Logic
What are our constraints?
a. Everyone belongs to at most one team.
b. Everyone belongs to at least one team.
c. The team partition structure is 8 + 8 + 8 + 3
d. The team partition structure is consistent
with the information in the game
\(p_A \implies (\neg q_A \land \neg r_A \land \neg s_A)\)
\(q_A \implies (\neg p_A \land \neg r_A \land \neg s_A)\)
\(r_A \implies (\neg p_A \land \neg q_A \land \neg s_A)\)
\(s_A \implies (\neg p_A \land \neg q_A \land \neg r_A)\)
Everyone belongs to at most one team.
\(p_Z \implies (\neg q_Z \land \neg r_Z \land \neg s_Z)\)
\(q_Z \implies (\neg p_Z \land \neg r_Z \land \neg s_Z)\)
\(r_Z \implies (\neg p_Z \land \neg q_Z \land \neg s_Z)\)
\(s_Z \implies (\neg p_Z \land \neg q_Z \land \neg r_Z)\)
\(\ldots\)
\(\ldots\)
\(\ldots\)
\(\ldots\)
\(p_A \lor q_A \lor r_A \lor s_A\)
Everyone belongs to at least one team.
\(p_B \lor q_B \lor r_B \lor s_B\)
\(p_Z \lor q_Z \lor r_Z \lor s_Z\)
\(\vdots\)
\(\cdots \large{\color{indianred}\lor} (p_A \land p_B \land p_C \land p_D \land p_W \land p_X \land p_Y \land p_Z) {\color{indianred}\lor} \cdots \)
\(\cdots \large{\color{indianred}\lor} \underbrace{(q_A \land q_B \land q_C \land q_D \land q_W \land q_X \land q_Y \land q_Z)}_{\text{a typical 8-sized subset of} \{ \text{ABCDEFGHIJKLMNOÖPQRSTUVQXYZ} \}} {\color{indianred}\lor} \cdots\)
\(\cdots\large{\color{indianred}\lor} (r_A \land r_B \land r_C \land r_D \land r_W \land r_X \land r_Y \land r_Z){\color{indianred}\lor} \cdots \)
\(\huge{\land}\)
\(\cdots \large{\color{indianred}\lor} (s_D \land s_M \land s_E){\color{indianred}\lor}\cdots\)
\(\huge{\land}\)
\(\huge{\land}\)
Any assignment of truth values to the 108 atomic variables will correspond to a valid partition of the population into R, B, G and BV.
We are looking for a specific partition among these.


\(\Huge{\oplus(q_E, q_G, q_Ö)}\)
\(\Huge{q_E \land q_H \land q_N}\)

Source: Rosen, 8th Edition, p. 76.
The Expressive Power of Propositional Logic
The Erdos Discrepancy Problem
The Expressive Power of Propositional Logic
Wumpus World: Reading Exercise
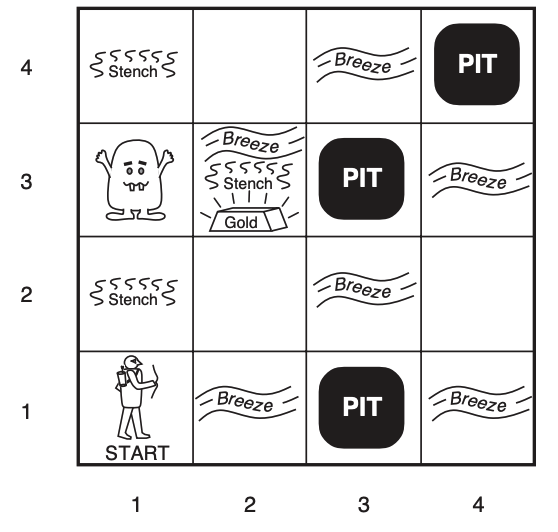
Source: Artificial Intelligence: A Modern Approach, Fourth Edition. Russell and Norvig
Sometimes, propositional logic is not expressive enough.
Suppose you want to assert that
there are infinitely many primes...?
Predicate Logic
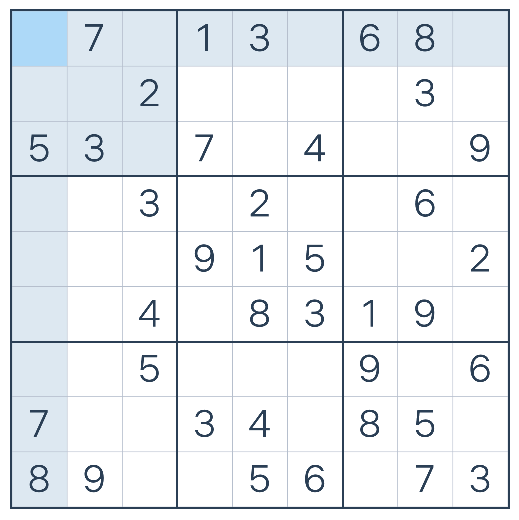
Sometimes, propositional logic is verbose.
Suppose you want to solve a sudoku problem.
Constraint Satisfaction Problems
A special class of search problems.
State is defined by variables \(X_i\) with values from a domain \(D\)
(sometimes \(D\) depends on \(i\))
The goal is to assign to each variable a value from its domain such that
all of a given set of constraints are satisfied.
Constraint Satisfaction
p
q
p 🤝 q
1
1
1
1
2
2
2
2
🆗
😢
😢
🆗
BYOTTB
(Bring Your Own Truth Tables)
Constraint Satisfaction Problems
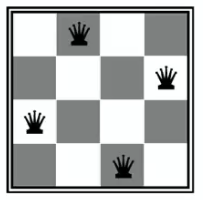
Example 1. The \(n\)-queens problem.
Variables: \(x_{ij}\)
Represent a position as follows:
\(x_{ij} \leftrightarrow 1\) iff
the cell in the i-th row and j-th column
is occupied by a queen
Constraints?
\(\begin{aligned}& \forall i, j, k\left(X_{i j}, X_{i k}\right) \in\{(0,0),(0,1),(1,0)\} \\& \forall i, j, k\left(X_{i j}, X_{k j}\right) \in\{(0,0),(0,1),(1,0)\} \\& \forall i, j, k\left(X_{i j}, X_{i+k, j+k}\right) \in\{(0,0),(0,1),(1,0)\} \\& \forall i, j, k\left(X_{i j}, X_{i+k, j-k}\right) \in\{(0,0),(0,1),(1,0)\}\end{aligned}\)
Row constraints
Column constraints
Diagonal constraints
\(\sum_{i, j} X_{i j}=N\)

Constraint Satisfaction Problems
Example 1. The \(n\)-queens problem.
Variables: \(Q_i\), \(1 \leqslant i \leqslant n\)
Represent a position as follows:
\(Q_{i} \leftrightarrow j\) iff
the cell in the i-th row and j-th column
is occupied by a queen
Constraints?
\(\forall i,j\) the queens in rows i and j
do not threaten each other.
\(Q_i, Q_j \notin \{ (1,1),(2,2),(3,3),(4,4),\cdots\}\)
Constraint Satisfaction Problems
Example 2. The IITGN Timetable
Suppose there are \(p\) classrooms, \(q\) slots, and \(r\) courses to be scheduled.
One classroom + one slot: at most one course
If two courses have overlaps, cannot be in the same slot.
A classroom has to be big enough for a course.
Etc.
Constraint Satisfaction Problems
Example 2. The IITGN Timetable
Variables: \(C_{ij}\), \(1 \leqslant i \leqslant p, 1 \leqslant j \leqslant q\)
The domain of \(C_{ij}\) is all the feasible cousres for classroom \(i\).
Constraints?
\(C_{ij}, C_{kj} \notin \{(a,b)~|~\text{if } a \text{ and } b \text{ are clashing}\}\).
Constraint Satisfaction Problems
Example 3. Cryptarithms

Variables: \(\{S,E,N,D,T,H,M,O,Y\}\)
Domain: \(\{0,1,2,3,4,5,6,7,8,9\}\)
Constraint Satisfaction Problems
Example 3. Cryptarithms

Variables: \(\{S,E,N,D,T,H,M,O,Y\}\)
Domain: \(\{0,1,2,3,4,5,6,7,8,9\}\)
Constraints:
\((D,E,Y) \in \{(0,1,1),(1,0,1),(1,2,3),\ldots\}.\)
\((S,E) \notin \{(0,0),(1,1),\cdots\}.\)
Distinctness constraints
Addition constraints
Constraint Satisfaction Problems
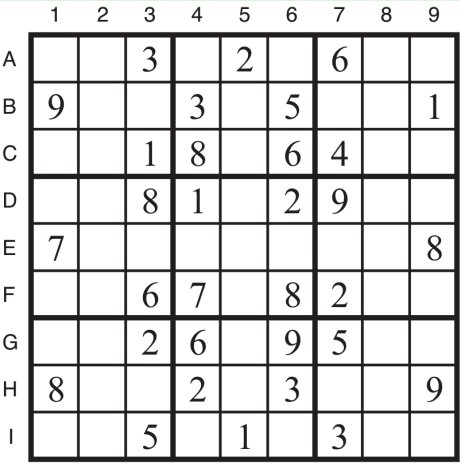
Example 4. Sudoku

Constraint Satisfaction Problems
Example 4. Sudoku

Constraint Satisfaction Problems
Example 4. Sudoku

Constraint Satisfaction Problems
Example 5. Waltz Algorithm from Computer Vision
Each intersection is a variable
Adjacent intersections impose constraints on each other
Solutions are physically realizable 3D interpretations
The Waltz algorithm is for interpreting line drawings of solid polyhedra as
3D objects
An early example of an Al computation posed as a CSP
Constraint Satisfaction Problems
Example 5. Waltz Algorithm from Computer Vision

Constraint Satisfaction Problems
Example 5. Waltz Algorithm from Computer Vision


Varieties of CSPs
Discrete Variables
Continuous variables
Finite domains
Infinite domains
Size \(d\) means \(O(d^n)\) complete assignments
Boolean SAT is a special case, NP-complete
Integers, strings; etc.
Linear constraints solvable, nonlinear undecidable
Linear constraints
(and more)
solvable efficiently
by LP methods
(out of scope)
Varieties of CSPs
Unary constraints involve a single variable (equivalent to reducing domains)
Binary constraints involve pairs of variables
Higher-order constraints involve 3 or more variables
Preferences (soft constraints)
e.g., paratha is better than pizza

Variables: \(Q_i\), \(1 \leqslant i \leqslant n\)
Represent a position as follows:
\(Q_{i} \leftrightarrow j\) iff
the cell in the i-th row and j-th column
is occupied by a queen
Constraints?
\(\forall i,j\) the queens in rows i and j
do not threaten each other.
\(Q_i, Q_j \notin \{ (1,1),(2,2),(3,3),(4,4),\cdots\}\)
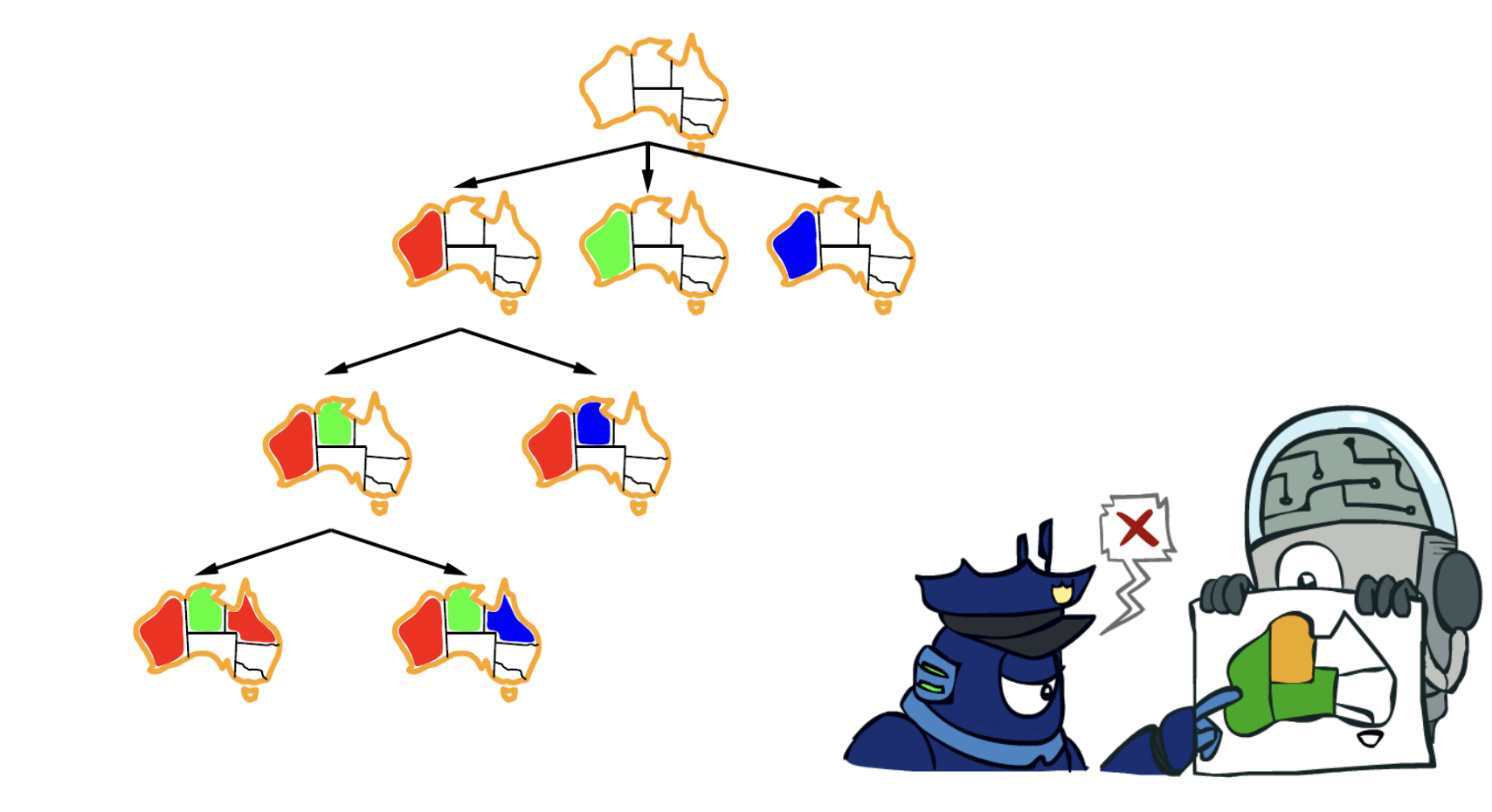
Expressing CSPs as Graphs
Four Queens Problem
Expressing CSPs as Graphs
Cryptarithms
D
E
Y
Expressing CSPs as Graphs
Cryptarithms
D
E
Y
CSPs in the wild
Assignment problems
Timetabling problems
Hardware configuration
Transportation scheduling
Factory scheduling
Circuit layout
Fault diagnosis
... lots more!


Solving Constraints
States defined by the values assigned so far (partial assignments)
An Initial Approach
Find a Satisfying Assignment by Search
• Initial state: the empty assignment, \(\emptyset\)
• To make progress: assign a value to an unassigned variable
• Stop test: the current assignment is complete and satisfies all constraints
An Initial Approach
Find a Satisfying Assignment by Search
\(\emptyset\)
\(x_1 = 1\)
\(x_1 = 2\)
\(\ldots\)
\(x_n = 7\)
The solutions are at the bottom layer
BFS will be forced to brute-force a lot before it gets to any solution.
DFS will hit complete solutions pretty quickly,
but no guarantees that they are correct.
An Initial Approach
Find a Satisfying Assignment by Search
\(\emptyset\)
\(x_1 = 1\)
\(x_1 = 2\)
\(\ldots\)
\(x_n = 7\)
We can exploit commutativity.
A problem is commutative if the order of application of any given set of actions has no effect on the outcome.
In this case the order of variable assignment does not change the result.
An Initial Approach
Find a Satisfying Assignment by Search
\(\emptyset\)
\(x_1 = 1\)
\(x_1 = 2\)
\(\ldots\)
\(x_n = 7\)
We can exploit commutativity.
A problem is commutative if the order of application of any given set of actions has no effect on the outcome.
In this case the order of variable assignment does not change the result.
An Initial Approach
Find a Satisfying Assignment by Search
\(\emptyset\)
\(x_1 = 1\)
\(x_1 = 2\)
\(\ldots\)
\(x_1 = 7\)
We can exploit commutativity.
A problem is commutative if the order of application of any given set of actions has no effect on the outcome.
In this case the order of variable assignment does not change the result.
An Initial Approach
Find a Satisfying Assignment by Search
\(\emptyset\)
\(x_1 = 1\)
\(x_1 = 2\)
\(\ldots\)
\(x_1 = 7\)
We can exploit commutativity.
A problem is commutative if the order of application of any given set of actions has no effect on the outcome.
In this case the order of variable assignment does not change the result.
An Initial Approach
Find a Satisfying Assignment by Search
\(\emptyset\)
\(x_1 = 1\)
\(x_1 = 2\)
\(\ldots\)
\(x_1 = 7\)
We can exploit commutativity.
A problem is commutative if the order of application of any given set of actions has no effect on the outcome.
In this case the order of variable assignment does not change the result.
Constraint Propagation Ideas
Node Consistency
A variable \(X_i\) is node-consistent if
if all the values in the variable’s domain
satisfy the variable’s unary constraints
A CSP is node-consistent if every variable is node-consistent
Node-consistency propagation: remove all values from the domain \(D_i\) of \(X_i\) which violate
unary constraints on \(X_i\).
Constraint Propagation Ideas
Arc Consistency
A variable \(X_i\) is arc-consistent with respect to another variable \(X_j\) if
for every value in the current domain \(D_i\)
there is some value in the domain \(D_j\)
that satisfies the binary constraint on the \(\operatorname{arc}\left(X_i, X_j\right)\).
A graph is arc-consistent if every variable is arc-consistent.
If \(X_i\) is not arc-consistent with the variable \(X_j\), we can make it consistent by removing values in \(D_i\) that is not consistent with any value on \(D_j\).
This removal can never rule out any solution.
Constraint Propagation Ideas
Arc Consistency
Answer on Menti:
For every binary constraint \(C\) involving variables \(X\) and \(Y\), if \(X\) is arc-consistent with respect to \(Y\) for \(C\), then \(Y\) is arc-consistent with respect to \(X\) for \(C\).
For every binary constraint \(C\) involving variables \(X\) and \(Y\), if \(X\) is arc-consistent with respect to \(Y\) for \(C\), then, after removing one value from the domain of \(Y\), \(X\) is still arc-consistent with respect to \(Y\) for \(C\).
Constraint Propagation Ideas
Forward Checking
Remove values from unassigned variables
which are not arc consistent with assigned variable
ensure arcs
from assigned to unassigned variables
are consistent
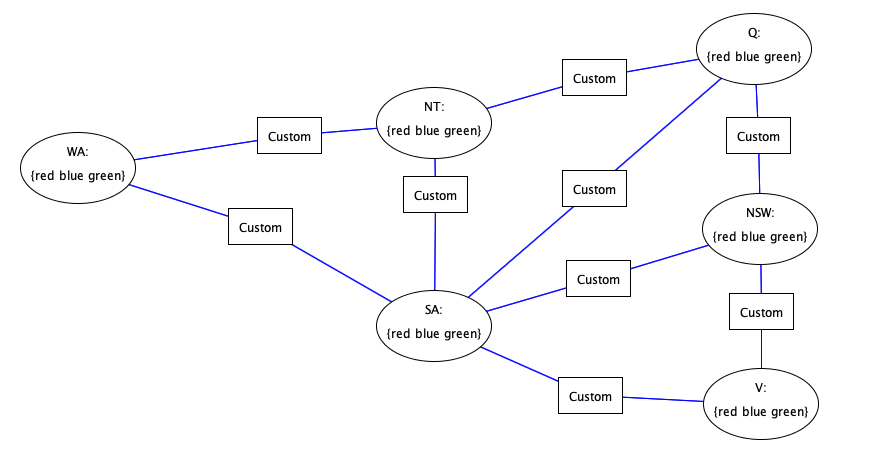
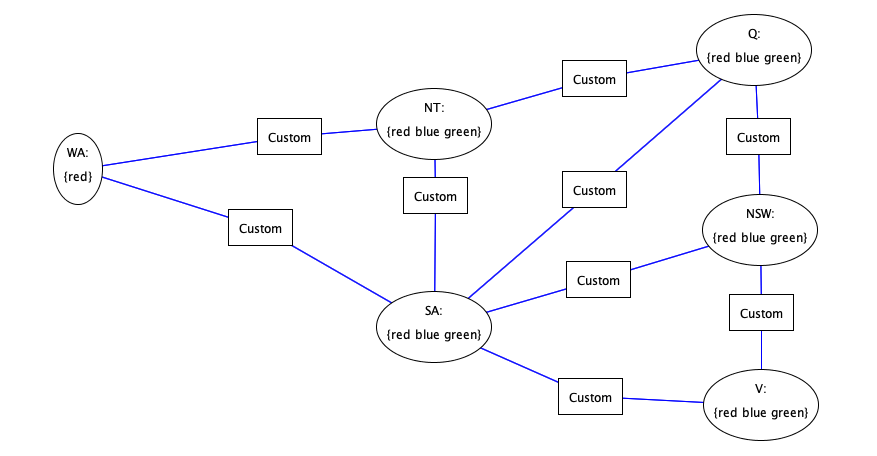
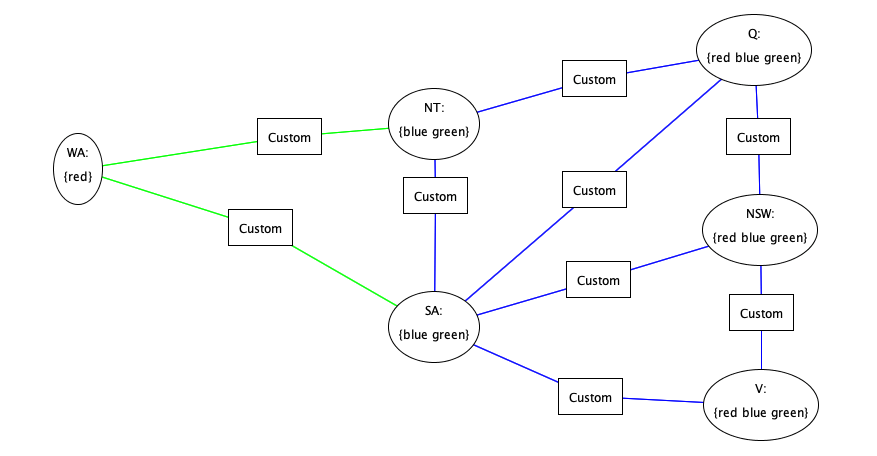
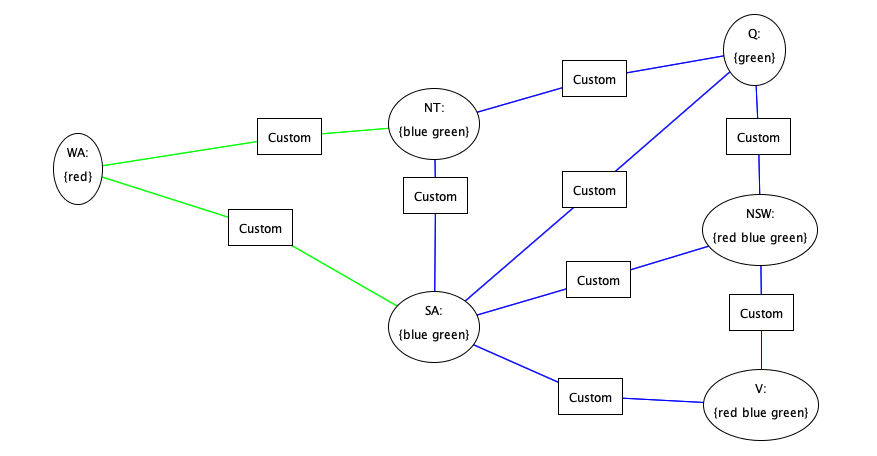
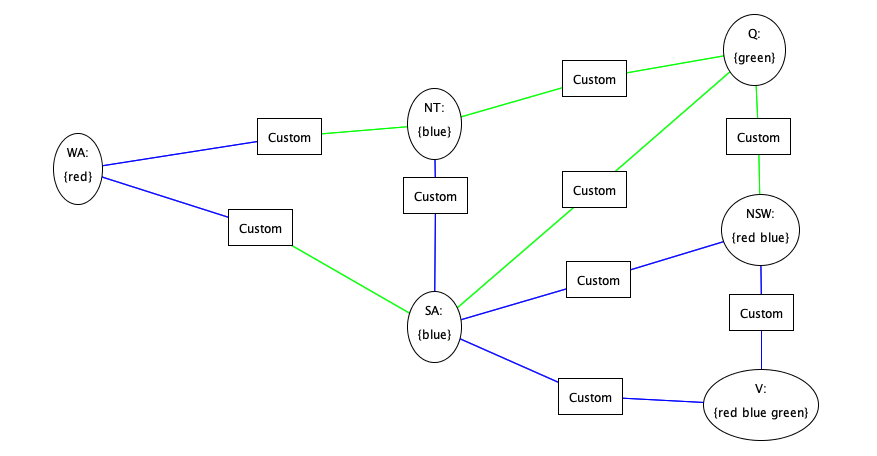

Constraint Propagation Ideas
Arc-consistency propagation
Remove all values from the domains of every variable
which are not arc-consistent with these
of some other variables
ensure all arcs are consistent!
Constraint Propagation Ideas
Arc Consistency

Constraint Propagation Ideas
Arc Consistency

Constraint Propagation Ideas
Arc Consistency

Constraint Propagation Ideas
Arc Consistency
Answer on Menti:
For four-queens, what do we get after performing arc-consistency checks starting at \(x_0 = 0\)?
\(\begin{aligned} & x_0=0, x_1 \in\{0,1,2,3\}, x_2 \in\{0,1,2,3\}, x_3 \in\{0,1,2,3\} \\ & x_0=0, x_1 \in\{1,2,3\}, x_2 \in\{1,2,3\}, x_3 \in\{1,2,3\} \\ & x_0=0, x_1 \in\{2,3\}, x_2 \in\{1,3\}, x_3 \in\{1,2\} \\ & x_0=0, x_1 \in\{3\}, x_2 \in\{1,3\}, x_3 \in\{2\}\end{aligned}\)
Constraint Propagation Ideas
Arc Consistency
Answer on Menti:
For four-queens, what do we get after performing forward checks starting at \(x_0 = 0\)?
\(\begin{aligned} & x_0=0, x_1 \in\{0,1,2,3\}, x_2 \in\{0,1,2,3\}, x_3 \in\{0,1,2,3\} \\ & x_0=0, x_1 \in\{1,2,3\}, x_2 \in\{1,2,3\}, x_3 \in\{1,2,3\} \\ & x_0=0, x_1 \in\{2,3\}, x_2 \in\{1,3\}, x_3 \in\{1,2\} \\ & x_0=0, x_1 \in\{3\}, x_2 \in\{1,3\}, x_3 \in\{2\}\end{aligned}\)
Backtracking
Backtracking

FAI · CSPs & Logic
By Neeldhara Misra
FAI · CSPs & Logic
- 1,498



