Data Structures and Algorithms
Graphs: An Introduction

executive summary
Graphs represent pairwise relationships between entities.
In these slides, we consider three common approaches to representing graphs: adjacency matrices, adjacency lists, and edge lists.
link to companion notes
Graphs
Model relationships between entities.
Graphs
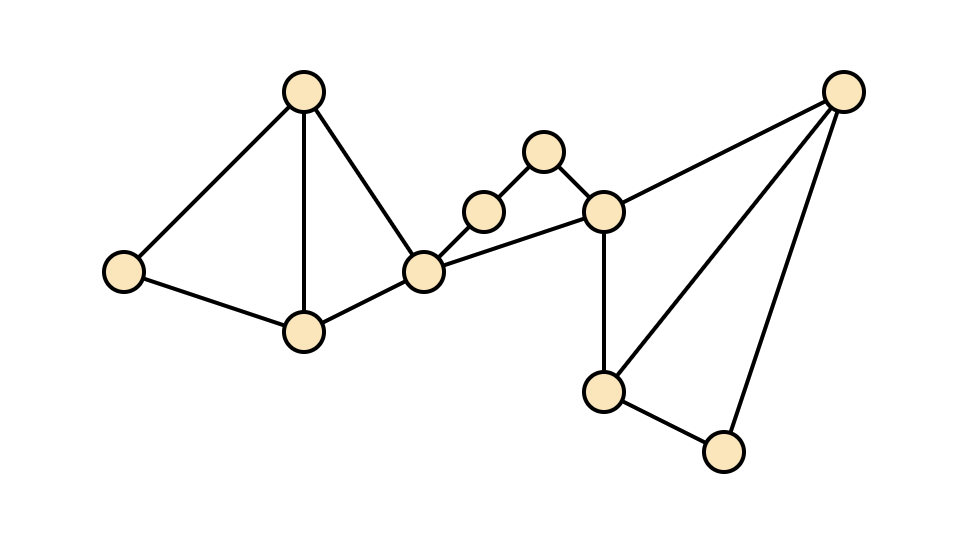
Common graphical representation: points & lines


1


1
2


1
2
3

1
2
3
4

1
2
3
4
5

1
2
3
4
5
6

1
2
3
4
5
6
7

1
2
3
4
5
6
7
8

1
2
3
4
5
6
7
8
9

1
2
3
4
5
6
7
8
9

1
2
3
4
5
6
7
8
9
Work through the exercises in the Mathigon lesson
about the Bridges of Königsberg
Graphs: Terminology
Vertices & Edges
Vertices are adjacent if there is an edge between them;
and they are the endpoints of said edge.
An edge is incident to its endpoints.
The (out)-neighbors of a vertex X are all the vertices Y such that (X,Y) is an edge.
The degree of a vertex is the number of neighbors it has.
Graphs can be...
Directed or Undirected
Vertex- and/or Edge-weighted
Simple or... not*
*graphs that are not simple are usually called multigraphs
Colored, temporal, hyper, etc.
Representing Graphs
1. Adjacency Matrix
2. Adjacency Lists
3. Edge Lists
Three popular styles.
a
c
e
b
d
f
Adjacency Matrix
a
c
e
b
d
f
a
a
b
c
d
e
f
b
c
d
e
f
Adjacency Matrix
a
c
b
f
a
a
b
c
d
f
b
c
e
f
e
d
e
d
Adjacency Matrix
a
a
b
c
d
f
b
c
e
f
e
d
0
a
c
e
b
d
f
Adjacency Matrix
c
e
d
f
a
c
d
e
f
b
c
d
e
f
a
b
0
a
b
Adjacency Matrix
a
c
e
b
d
f
a
c
d
e
f
b
c
d
e
f
a
b
0
1
Adjacency Matrix
a
c
e
b
d
f
a
c
d
e
f
b
c
d
e
f
a
b
1
1
1
1
1
1
1
1
1
1
Adjacency Matrix
a
c
e
b
d
f
a
c
d
e
f
b
c
d
e
f
a
b
1
1
1
1
1
1
1
1
1
1
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
Adjacency Matrix
a
c
e
b
d
f
a
c
d
e
f
b
c
d
e
f
a
b
1
1
1
1
1
1
1
1
1
1
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
Adjacency Matrix
a
c
e
b
d
f
a
c
d
e
f
b
c
d
e
f
a
b
1
1
1
1
1
1
1
1
1
1
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
Adjacency List
a
c
e
b
d
f
Adjacency List
a
c
e
b
d
f
a
c
d
e
f
b
Adjacency List
e
d
f
c
d
e
f
b
c
b
b
c
a
a
Adjacency List
a
e
d
f
a
c
d
e
f
b
c
b
b
c
a
Adjacency List
a
d
e
f
b
c
b
b
c
a
a
a
d
e
e
d
f
c
Adjacency List
a
c
e
f
b
c
b
b
c
a
a
a
d
e
e
d
f
c
d
Adjacency List
a
c
d
f
b
c
b
b
c
a
a
a
d
e
e
d
f
c
c
f
e
Adjacency List
a
c
d
b
c
b
b
c
a
a
a
d
e
e
d
f
c
c
f
e
e
f
Adjacency List
a
c
d
b
c
b
b
c
a
a
a
d
e
e
d
f
c
c
f
e
e
f
Edge List
a
e
d
f
c
b
Edge List
a
e
d
f
c
b
a
b
1.
Edge List
a
e
d
f
c
b
a
b
1.
c
d
2.
Edge List
a
e
d
f
c
b
a
b
1.
c
d
2.
e
f
3.
Edge List
a
e
d
f
c
b
a
b
1.
c
d
2.
e
f
3.
a
c
4.
Edge List
a
e
d
f
c
b
a
b
1.
c
d
2.
e
f
3.
a
c
4.
c
e
5.
Edge List
a
e
d
f
c
b
a
b
1.
c
d
2.
e
f
3.
a
c
4.
c
e
5.
Official Running Times
Brilliant.
When the procedure only needs constant time.
Decent.
When the procedure always wraps up in, and sometimes needs,
time proportional to the maximum degree of the graph.
(n/m)-tolerable.
When the procedure always wraps up in, and sometimes needs,
time proportional to the number of vertices/edges in the graph.
(n/m)-painful.
When the procedure always wraps up in, and sometimes needs,
time proportional to the number of vertices/edges in the graph squared.
| Adj. Matrix | Adj. List | Edge List | |
|---|---|---|---|
| Adding a vertex | |||
| Deleting a vertex | |||
| Adding an edge | |||
| Deleting an edge | |||
| Finding degree(v) | |||
| Check if (u,v) is an edge |
| Adj. Matrix | Adj. List | Edge List | |
|---|---|---|---|
| Adding a vertex | Painful | ||
| Deleting a vertex | Painful | ||
| Adding an edge | Brilliant | ||
| Deleting an edge | Brilliant | ||
| Finding degree(v) | Tolerable | ||
| Check if (u,v) is an edge | Brilliant |
| Adj. Matrix | Adj. List | Edge List | |
|---|---|---|---|
| Adding a vertex | Painful | Tolerable | |
| Deleting a vertex | Painful | Tolerable | |
| Adding an edge | Brilliant | Brilliant | |
| Deleting an edge | Brilliant | Decent | |
| Finding degree(v) | Tolerable | Decent | |
| Check if (u,v) is an edge | Brilliant | Decent |
| Adj. Matrix | Adj. List | Edge List | |
|---|---|---|---|
| Adding a vertex | Painful | Tolerable | Decent |
| Deleting a vertex | Painful | Tolerable | Tolerable |
| Adding an edge | Brilliant | Brilliant | Brilliant |
| Deleting an edge | Brilliant | Decent | Tolerable |
| Finding degree(v) | Tolerable | Decent | Tolerable |
| Check if (u,v) is an edge | Brilliant | Decent | Tolerable |
DSA · Introduction to Graphs
By Neeldhara Misra
DSA · Introduction to Graphs
Data Structures: Just some Structured Data
- 1,142



