Quasi-probabilities on Fermionic Phase Spaces
Ninnat Dangniam, Christopher Jackson, Carlton Caves
Center for Quantum Information and Control, University of New Mexico
Christopher Ferrie
Centre for Quantum Software and Information, University of Technology Sydney
SQuInT, 23 February 2018
Why Quasi-probability?
| "Resources" |
|---|
| Negativity Contextuality Bell non-locality Entanglement Interference Quantum speed-up |
| Tools |
|---|
| Quasi-probability Covariance matrix Stabilizer formalism Matrix product state Monte Carlo Computational complexity |
|
Contextuality Bell non-locality Entanglement Interference Quantum speed-up |
|
Covariance matrix Stabilizer formalism Matrix product state Monte Carlo Computational complexity |
Negativity
Quasi-probability
"Resources"
Tools
Why Quasi-probability?
Positive quasi-probabilities
Monte Carlo
Classical simulation
Why Quasi-probability?
Monte Carlo
Classical simulation
Negative quasi-probabilities
No classical simulation
Why Quasi-probability?
Efficiently representable
positive quasi-probabilities
Negativity is a necessary but not sufficient quantum resource
Veitch et al., New J. Phys. 14 113011 (2012)
| Free states/ Operations | Wigner function | Discrete Wigner function (Odd dimensions only) |
|---|---|---|
| Positive pure states | Gaussians (Hudson thm) |
Stabilizer states (Discrete Hudson thm) |
| (Non-convex-Gaussian) positive mixed states | e.g. Single-photon-added thermal states |
"Bounded universal" states |
| Operations | Quadratic bosonic Hamiltonians | Cliffords |
| Measurements | Gaussians | Paulis |
Veitch et al., New J. Phys. 15 013037 (2013)
Bartlett et al., Phys. Rev. Lett. 88 097904 (2002)
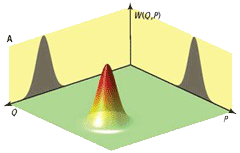
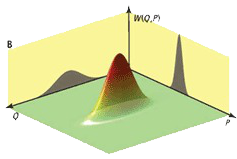
Q functions are always positive
Q(\alpha) = \langle \alpha|\rho|\alpha \rangle
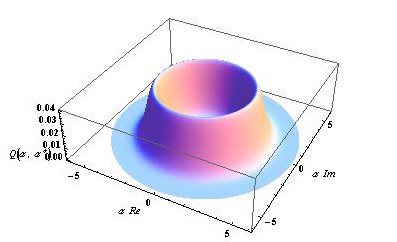
Q function of a photon number state
"In evaluating the possibility of a classical explanation of an experiment, one must consider the negativity of not just the representation of [states] but of measurements as well, and one must look at representations other than that of Wigner."
Spekkens, Phys. Rev. Lett. 101 020401 (2008)
This Talk
\rho
E
State
\mu_{\rho}(\Omega) = \text{Tr}[\rho F(\Omega)]
Measurement
\zeta_{E_k}(\Omega) = \text{Tr}[E_k D(\Omega)]
Quasi-probability Representations
Outcome k
Hermitian
Hermitian
Quantum experiment
\text{Tr}[A
A = \int d\Omega \, \text{Tr}[AF(\Omega)]
A
A
F(\Omega)
]
Frame
D(\Omega)
Dual frame
F(\Omega)
D(\Omega)
Frames and Their Duals
\text{Tr}[A
A = \int d\Omega \, \text{Tr}[A|\alpha \rangle \langle \alpha|]
A
A
|\alpha \rangle \langle \alpha|
]
Frame
D(\Omega)
Dual frame
F(\Omega)
D(\Omega)
Frames and Their Duals
Frame for the
Q function
Frame for the P function
\rho
E
State
\mu_{\rho}(\Omega) = \text{Tr}[\rho F(\Omega)]
Measurement
\zeta_{E_k}(\Omega) = \text{Tr}[E_k D(\Omega)]
P(E_k|\rho) = \text{Tr}[E_k \rho] = \int d\Omega \, \mu_{\rho} (\Omega) \zeta_{E_k} (\Omega)
Quasi-probability Representations
Born rule as phase space average
Outcome k
Hermitian
Hermitian
Quantum experiment
The frame or the dual frame must contain a non-positive operator
Spekkens, Phys. Rev. Lett. 101 020401 (2008)
Ferrie and Emerson, J. Phys. A: Math. Theor. 41 352001 (2008)
Quasi-probability Representations
\rho
E
State
Measurement
Quantum experiment
Fermions
Veitch et al., New J. Phys. 14 113011 (2012)
| Wigner function | Discrete Wigner function (Odd dimensions only) |
|
|---|---|---|
| Positive pure states | Gaussians (Hudson thm) |
Stabilizer states (Discrete Hudson thm) |
| (Non-convex-Gaussian) positive mixed states | e.g. Single-photon-added thermal states |
"Bounded universal" states |
| Operations |
|
Cliffords |
| Measurements | Gaussians | Paulis |
Veitch et al., New J. Phys. 15 013037 (2013)
Bartlett et al., Phys. Rev. Lett. 88 097904 (2002)
Free states/ Operations
Quadratic bosonic Hamiltonians
Reversible free operations simply permute points of the phase space
U(g) F(\Omega) U^{\dagger}(g) = F(g \cdot \Omega)
G-covariant frame
Free operations should not increase "resource" (negativity)
The Wigner frame is self-dual and covariant w.r.t. all quadratic bosonic Hamiltonian evolutions
\{ a_j, a^{\dagger}_k \} = \delta_{jk}
H = \sum_{jk}
Quadratic Fermionic Hamiltonians
Free Fermionic Evolution
\{ a_j, a_k \} = 0
\alpha_{jk} a_j^{\dagger}a_k
+
\beta_{jk} a_j^{\dagger} a_k^{\dagger}
+ \text{H.C.}
Number-preserving
Squeezing
\{ c_{\alpha}, c_{\beta} \} = 2 \delta_{\alpha \beta}
Majorana operators
a_j = \displaystyle{\frac{c_{2j-1} + ic_{2j}}{2}}
Quadratic Fermionic Hamiltonians
Free Fermionic Evolution
H = \frac{i}{4} \sum_{\alpha\beta,\alpha < \beta}
h_{\alpha\beta}
[c_{\alpha},c_{\beta}]
Antisymmetric
\{ a_j, a^{\dagger}_k \} = \delta_{jk}
\{ a_j, a_k \} = 0
Majorana operators
\{ c_{\alpha}, c_{\beta} \} = 2 \delta_{\alpha \beta}
a_j = \displaystyle{\frac{c_{2j-1} + ic_{2j}}{2}}
Quadratic Fermionic Hamiltonians
Free Fermionic Evolution
H = \frac{i}{4} \sum_{\alpha\beta,\alpha < \beta}
h_{\alpha\beta}
[c_{\alpha},c_{\beta}]
Antisymmetric
\vec{c}(t) = e^{\bold{h}t} \vec{c}(0)
\bold{h}
\text{SO(2n)}
\in
Group of rotations
in 2n dimensions
\begin{pmatrix}
c_1 \\
c_2 \\
\vdots \\
c_{2n}
\end{pmatrix}
| \Omega \rangle = U(g) |0 \rangle
The group action on the vacuum define an SO(2n)-covariant Q Function
Orbit
Coset space
Number-preserving
- Perelomov, Generalized Coherent States... (1986)
- Zhang, Feng and Gilmore, Rev. Mod. Phys. 62 867 (1990)
\{\Omega \} = \text{SO}(2n)/\text{U(n)}
Fermionic Gaussian states
Phase space
=
Q(\alpha) = \langle \Omega|\rho|\Omega \rangle
Q function
S^2 \simeq \text{SO}(3)/\text{SO}(2)
|n\rangle
\theta
\phi
|0\rangle
Guiding Example
Q functions on a sphere for spin-j systems
Spherical Q Function
R(\eta,\theta,\phi) = R_Z(\phi) R_Y(\theta) R_Z(\eta)
|\langle n|m \rangle|^2 = \frac{(1+\cos\theta)}{2}^{2j}
Quasi-probability representation for spin-j systems
|n\rangle
\theta
\phi
|0\rangle
n
m
Spherical Q Function
R_{n \to m}
R(\eta,\theta,\phi) = R_Z(\phi) R_Y(\theta) R_Z(\eta)
|\langle n|m \rangle|^2 = \frac{(1+\cos\theta)}{2}^{2j}
Quasi-probability representation for spin-j systems
|n\rangle
\phi
|0\rangle
\theta
0
0
Spherical Q Function
R_Y
R_Z
R(\eta,\theta,\phi) = R_Z(\phi) R_Y(\theta) R_Z(\eta)
|\langle n|m \rangle|^2 = \frac{(1+\cos\theta)}{2}^{2j}
Quasi-probability representation for spin-j systems
|n\rangle
\phi
|0\rangle
R_Z
0
0
\theta
Spherical Q Function
R(\eta,\theta,\phi) = R_Z(\phi) R_Y(\theta) R_Z(\eta)
|\langle n|m \rangle|^2 = \frac{(1+\cos\theta)}{2}^{2j}
Quasi-probability representation for spin-j systems
|n\rangle
\phi
|0\rangle
\theta
R_Y
0
0
|0\rangle
|0\rangle
|0\rangle
R_{Y^+}
|0\rangle
R_{Z^+}
R_{Y^-}
R_{Z^-}
Fermionic Q Function
\text{U}(4)
2 commuting
two-mode squeezings
|\langle \Omega|\Omega' \rangle|^2 = (\frac{1+\cos \theta^+_{12}}{2}) (\frac{1+\cos \theta^+_{34}}{2})
Number-preserving
R_{Y^+}
R_{Z^+}
R_{Y^-}
R_{Y^-}
R_{Y^-}
R_{Z^-}
R_{Z^-}
R_{Z^-}
Jordan-Wigner transform to 4-qubit quantum circuit
|0\rangle
|0\rangle
|0\rangle
R_{Y^+}
|0\rangle
R_{Z^+}
R_{Y^-}
R_{Z^-}
Fermionic Q Function
\text{U}(4)
commuting
two-mode squeezings
|\langle \Omega|\Omega' \rangle|^2 = (\frac{1+\cos \theta^+_{12}}{2}) (\frac{1+\cos \theta^+_{34}}{2})
Number-preserving
R_{Y^+}
R_{Z^+}
R_{Y^-}
R_{Y^-}
R_{Y^-}
R_{Z^-}
R_{Z^-}
R_{Z^-}
\lfloor \frac{n}{2} \rfloor
Jordan-Wigner transform to 4-qubit quantum circuit
|\langle \Omega|\Omega' \rangle|^2 = |\langle 0| U^{\dagger}(\Omega) U(\Omega') |0 \rangle|^2
= |\langle 0| U(\Omega^{-1}\Omega') |0 \rangle|^2
= |\langle 0| U(Kg^{-1}g'K') |0 \rangle|^2
U(n)-bi-invariant function
Fermionic Q Function
\in \text{Span}\{ \lfloor \frac{n}{2} \rfloor + 1 \, \, \text{zonal spherical functions} \}
K = \text{U}(n)
From the Q function, we can generate a continuous family of G-covariant frames and dual frames that gives a unique self-dual "Wigner function"
F^{(s)}(\Omega) = \int d\Omega' \,
\text{Tr} [F^{(s)}(\Omega) F^{(1)}(\Omega')]
|\Omega' \rangle \langle \Omega'|
P
Q
Wigner
s
-1
0
1
Stratonovich-Weyl axioms
Brif and Mann, Phys. Rev. A 59 971 (1999)
Fermionic Wigner Function
From the Q function, we can generate a continuous family of G-covariant frames and dual frames that gives a unique self-dual "Wigner function"
P
Q
Wigner
s
-1
0
1
Stratonovich-Weyl axioms
= \text{Tr} [U(\Omega) F^{(s)}(0) U^{\dagger}(\Omega) U(\Omega') F^{(-s')}(0) U^{\dagger}(\Omega')]
= \text{Tr} [F^{(s)}(0) U(\Omega^{-1}\Omega') ^{(-s')}F(0) U^{\dagger}(\Omega^{-1}\Omega')]
U(n)-bi-invariant function!
\text{Tr} [F^{(s)}(\Omega) F^{(s')}(\Omega')]
Fermionic Wigner Function
Brif and Mann, Phys. Rev. A 59 971 (1999)
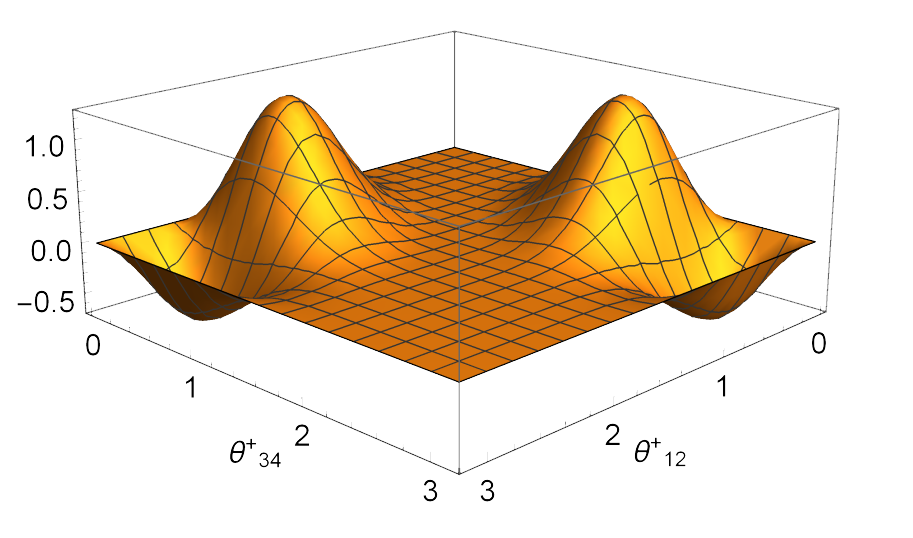
4-mode fermionic Gaussian state
Fermionic Wigner Function
4-mode fermionic Gaussian state
- Closest analogue, but may not be a fair comparison to bosonic quasi-probability representations
- The continuous family of bosonic quasi-probability representations are not covariant under the full quadratic Hamiltonian evolution
- There is no analogue of the Heisenberg group for fermions
Why Negativity?
- Scaling of negativity and simulatability
- Negativity of non-Gaussian states
- Connection to existing quasi-probability representations for fermions
Future Directions
Summary
- We define quasi-probability representations in terms of frames and dual frames.
- We obtain a continuous family of SO(2n)-covariant quasi-probability representations from fermionic Gaussian states.
- We prove the uniqueness of the self-dual "Wigner function".
- The construction applies to phase spaces that are symmetric homogeneous spaces and more.
ND, "Quantum Phase Space Representations and Their Negativities", University of New Mexico, PhD Dissertation (2018)
Fermion phase spaces
By Ninnat Dangniam
Fermion phase spaces
SQuInT, Santa Fe, 23 February 2018
