Competition of trivial and topological phases in graphene based hybrid systems
Zoltán Tajkov
PhD Student
Department of Biological Physics, Eötvös Loránd University
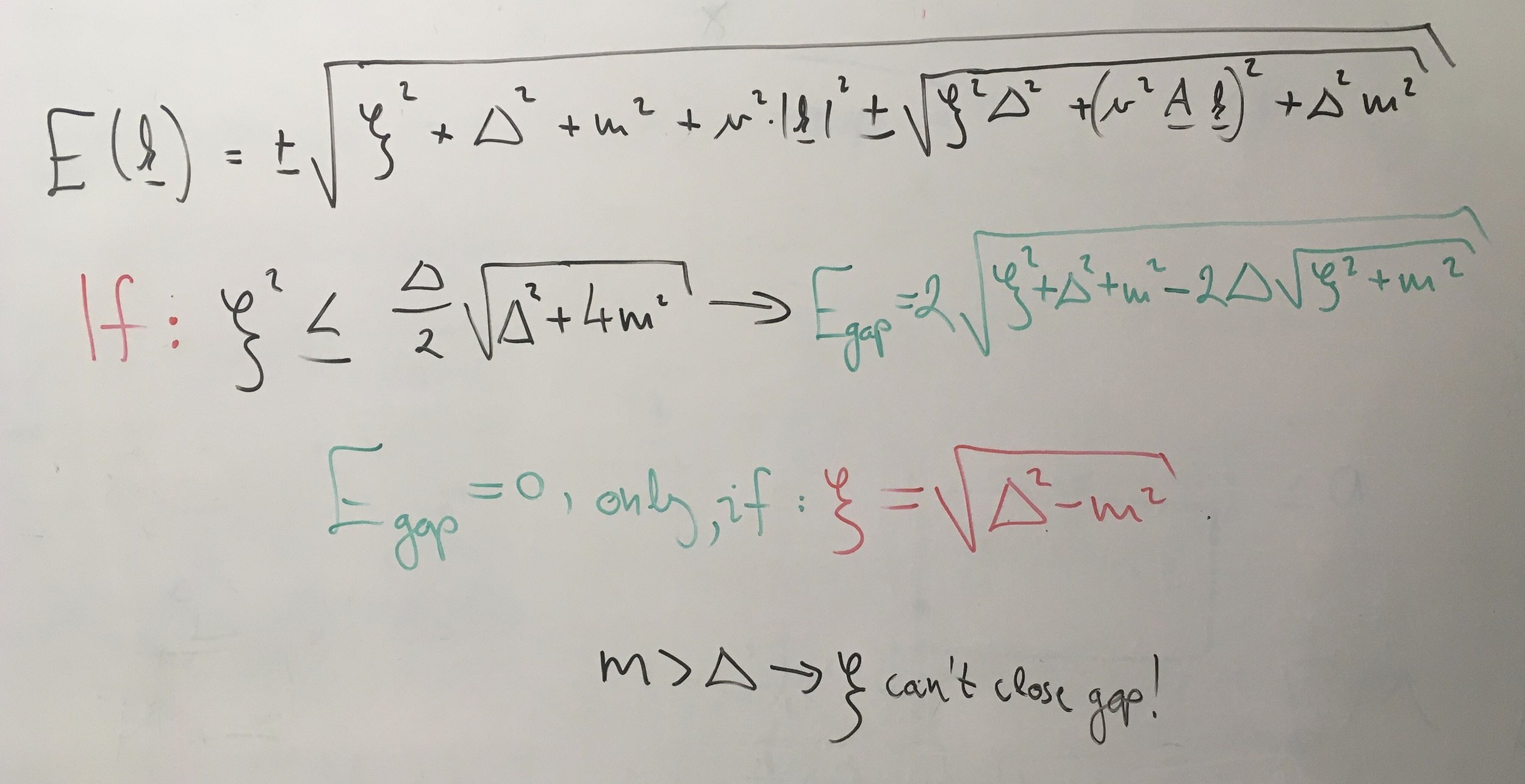
Seminar of Condensed Matter Theory Groups in Regensburg
19. May, 2021.
Graphene is ...
A. K. Geim, I. V. Grigorieva Nature 499, 419 (2013)
Graphene is ...
... a good template!
A. K. Geim, I. V. Grigorieva Nature 499, 419 (2013)
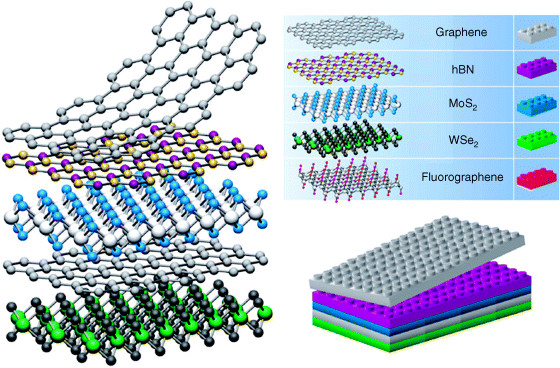
Graphene is ...
... a good template!
A. K. Geim, I. V. Grigorieva Nature 499, 419 (2013)
How can we induce topological phase into graphene?
Graphene is ...
... a good template!
C. L. Kane, E. J. Mele, PRL 95, 226801 (2005)
How can we induce topological phase into graphene?
SOC!!
J. Sichau et. al. PRL 122, 046403 (2019)
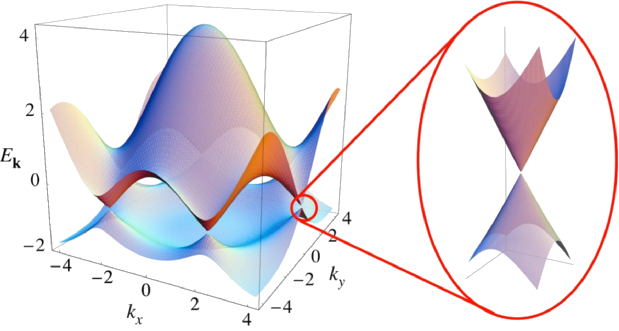
How strong is the effect?
SOC!!
Intrinsic spin-orbit coupling is weak in graphene!
\Delta E_{\mathrm{SOI}}=\left( 42.2 \pm 0.8 \right) \mu \mathrm{eV}
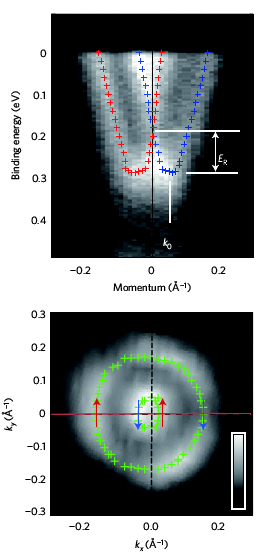
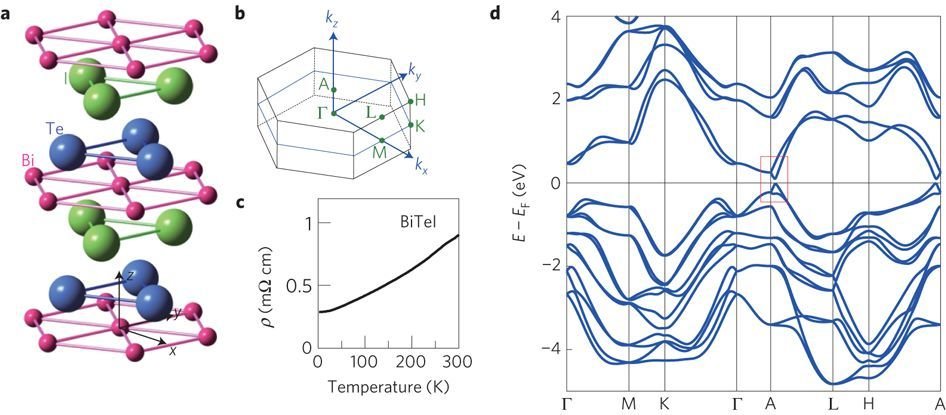
BiTeX: giant SOC
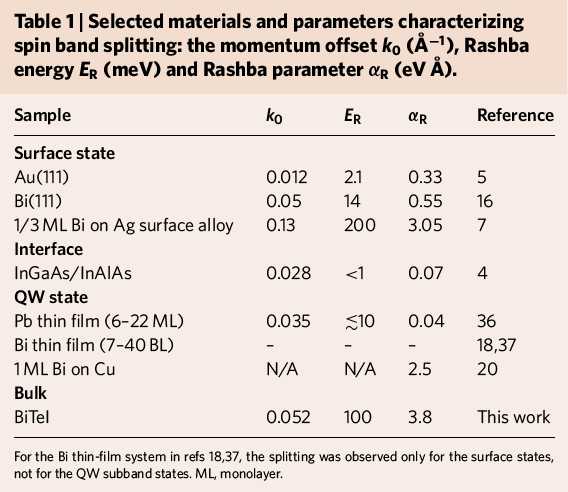
Ishizaka et al. Nature Materials 10, 521 (2011)
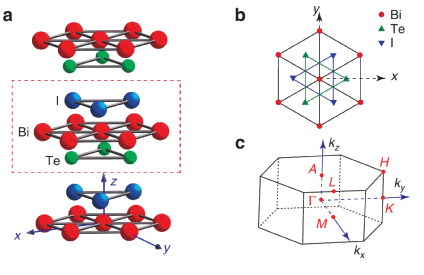
BiTeX monolayer
Fülöp et al. 2D Mater. 5, 031013 (2018)
BiTeX/graphene heterostructures
BiTeI sandwich: Kou et al. ACS Nano, 8 10448 (2014)
BiTeX/graphene heterostructures
Z. Tajkov et al. Nanoscale 11, 12704 (2019)
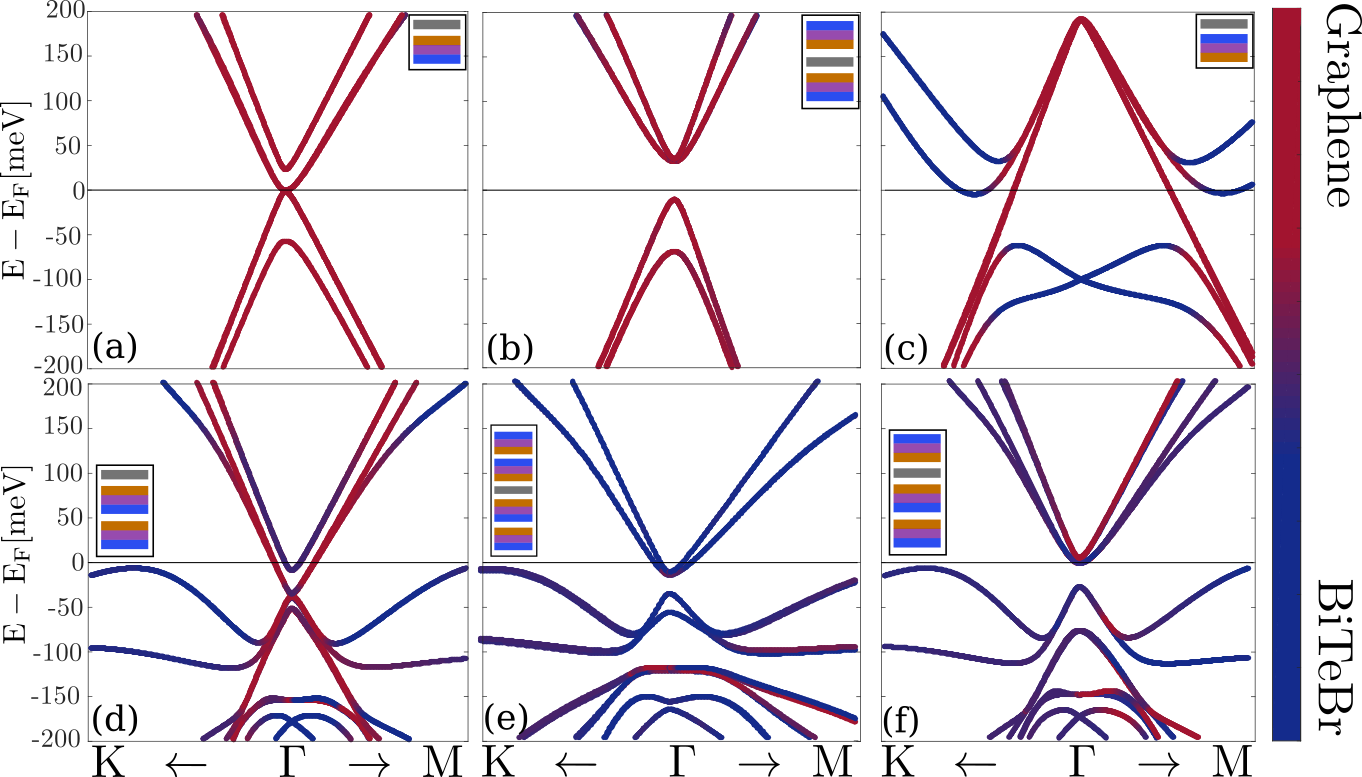
DFT (SIESTA) results
topological
trivial
Sandwich:
~40 meV topological gap
One sided:
~1 meV trivial gap
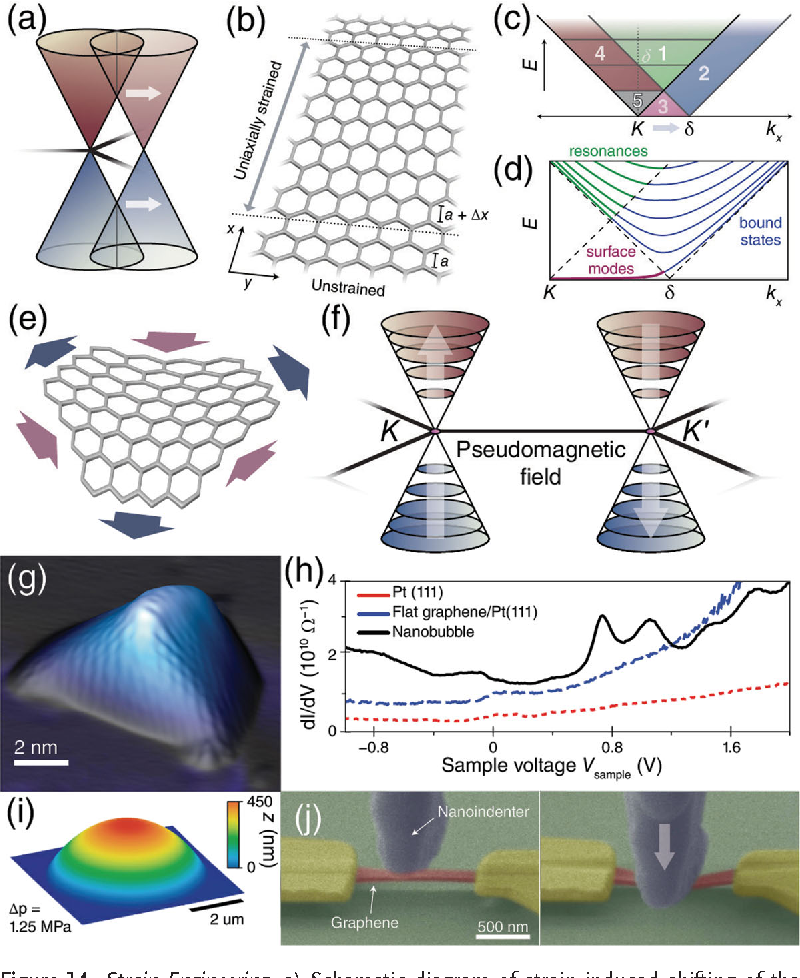
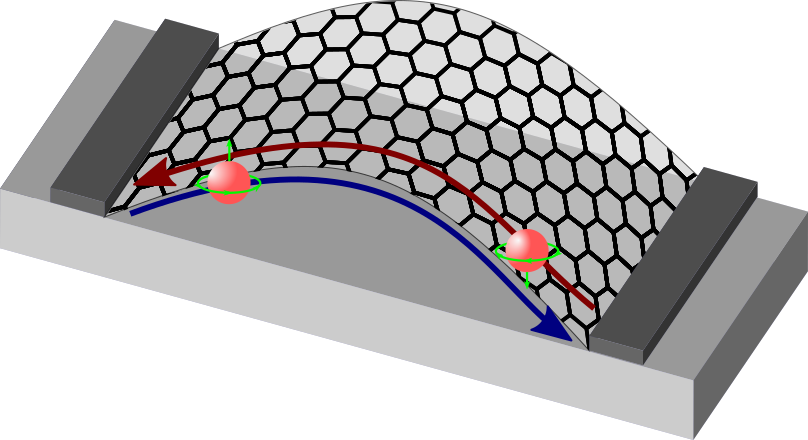
Mechanical distortions
in graphene
Weiss et al. Advanced Materials, 24 5782(2012)
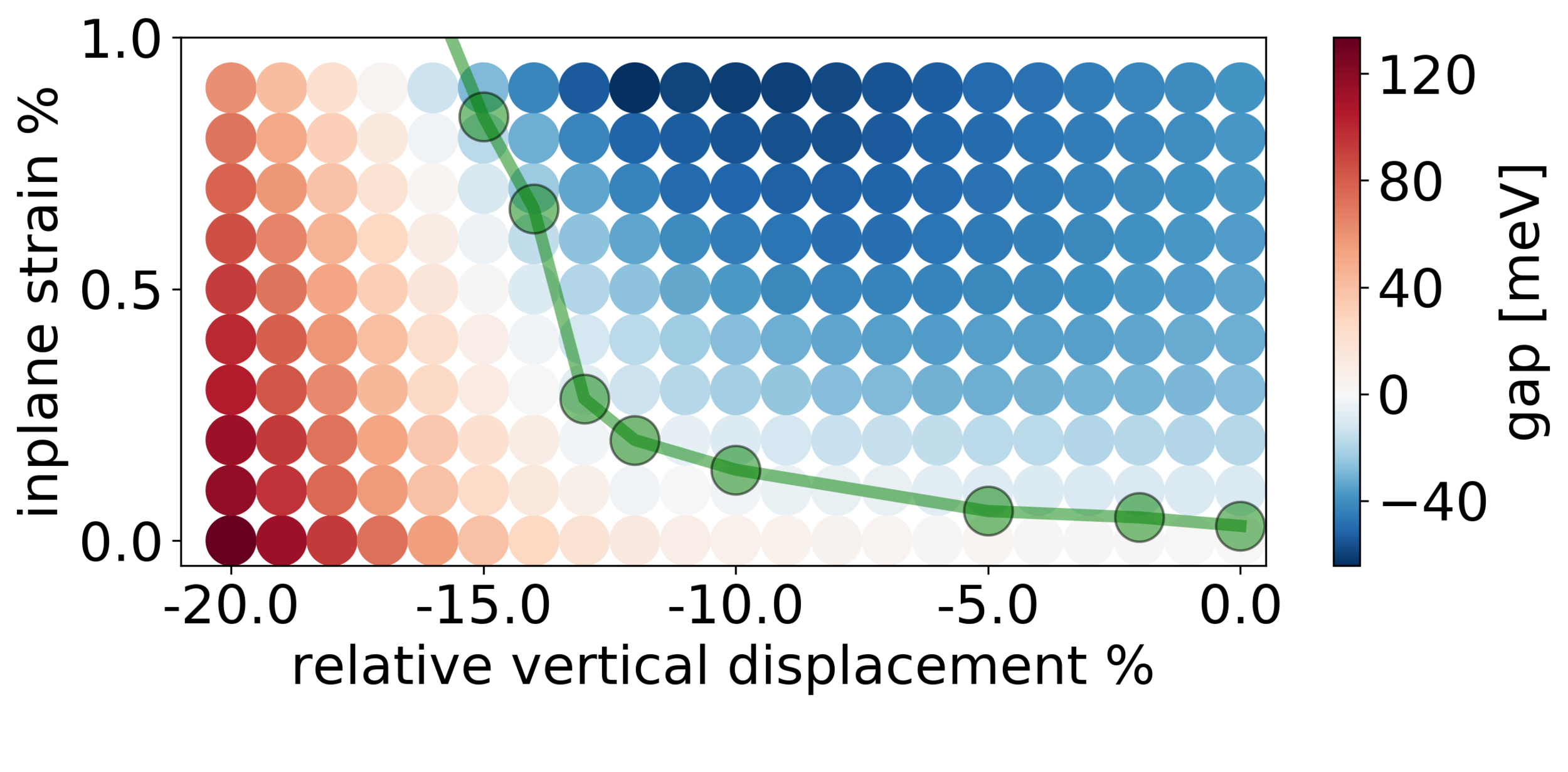
Pressure→I, inplane strain →TI !?!
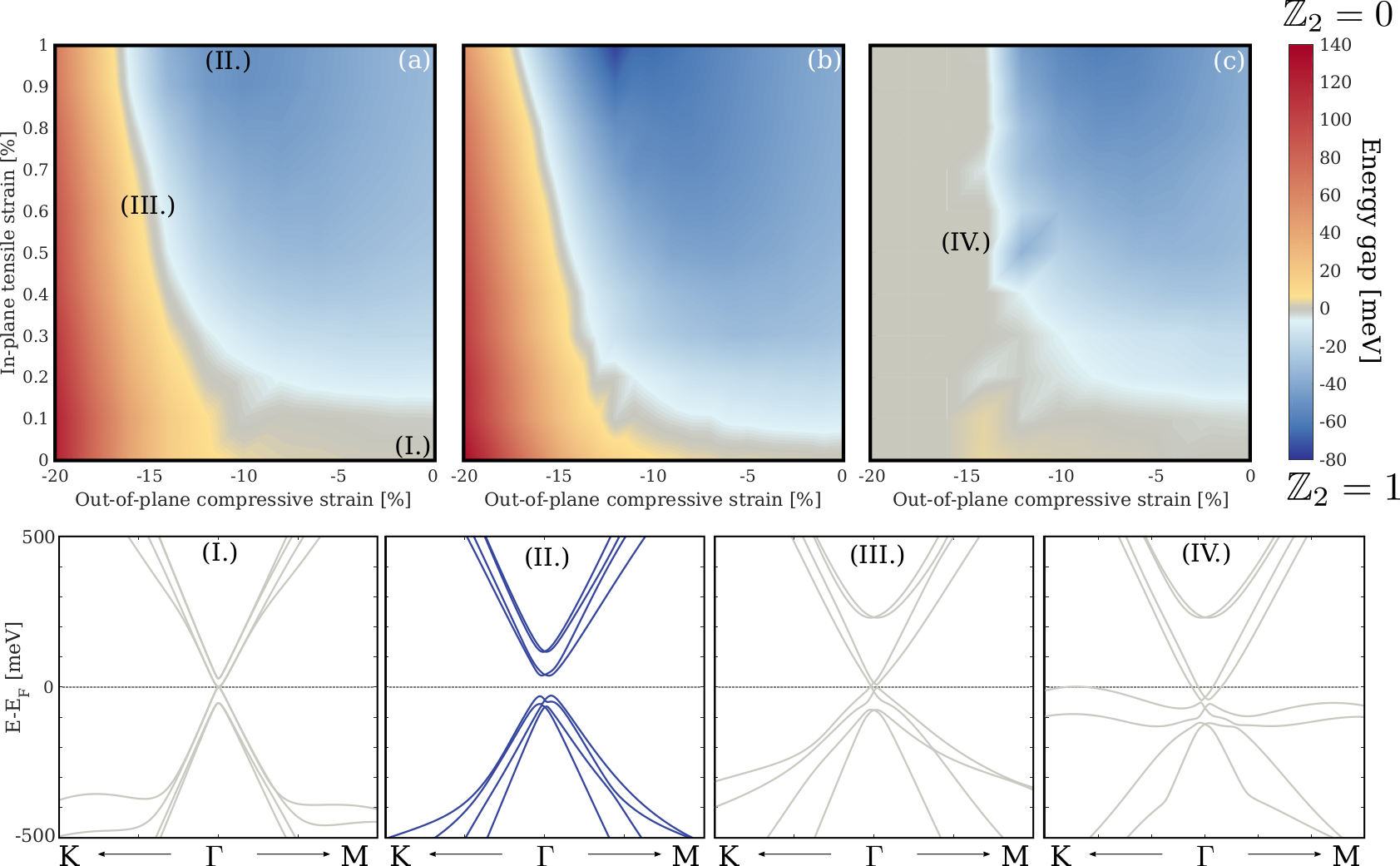
Z. Tajkov et al. Appl. Sci. 9, 4330 (2019)
BiTeBr
BiTeCl
BiTeI
BiTeI is different, why?
More DFT!!
Why does BiTeI behave differently?
Z. Tajkov et al. Appl. Sci. 9, 4330 (2019)
BiTeCl / BiTeBr, graphene
BiTeI, graphene
\(E_\mathrm{F} \) for graphene
\(E_\mathrm{F} \) for BiTeX
WF are different!
- Graphene: 4.6 eV
- BiTeCl/Br: 4.7–4.5 eV
- BiTeI : 5.1 eV
Effective model and fit
t_1+i\vec{m_1}\cdot\vec{\sigma}
t_2+i\vec{m_2}\cdot\vec{\sigma}
t_3+i\vec{m_3}\cdot\vec{\sigma}
im_z\sigma_z
=\mathrm{e}^{-\beta\left(l/l_0-1\right)}
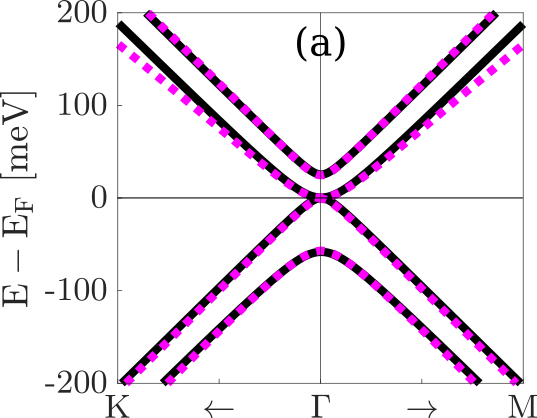
TB model predicts phase transition well!
topological
trivial
Z. Tajkov et al. Nanoscale 11, 12704 (2019)
What did we learn from DFT?
The most important parameters
Kekulé
Kane-Mele
Strain promotes SOC \( \rightarrow \) TI
Technical details of the model
We have to deal with:
- Graphene
- Kekulé
- Kene-Male
- Strain
Divide et impera
Start with graphene + strain
\boldsymbol{a}_{2,1} =a_{\mathrm{cc}}\frac{1}{2}\left(\begin{array}{c}
\pm\sqrt{3}\\
3
\end{array}\right)
\boldsymbol{b}_{2,1} =\left(\begin{array}{c}
\pm\frac{2\sqrt{3}}{3a_{\mathrm{cc}}}\pi\\
\frac{2}{3a_{\mathrm{cc}}}\pi
\end{array}\right)
\boldsymbol{\delta}_{1}=\left(\begin{array}{c}
0\\
-1
\end{array}\right) \\
\boldsymbol{\delta}_{2}=\frac{1}{2}\left(\begin{array}{c}
\sqrt{3}\\
1
\end{array}\right)\\
\boldsymbol{\delta}_{3}=\frac{1}{2}\left(\begin{array}{c}
-\sqrt{3}\\
1
\end{array}\right) \\
d_{1}=t_{0}\mathrm{e}^{-\beta\left(\frac{|\left(\boldsymbol{\varepsilon}+1\right)\boldsymbol{\delta}_{1}|}{a_{0}}-1\right)} \\
d_{2}=t_{0}\mathrm{e}^{-\beta\left(\frac{|\left(\boldsymbol{\varepsilon}+1\right)\boldsymbol{\delta}_{2}|}{a_{0}}-1\right)} \\
d_{3}=t_{0}\mathrm{e}^{-\beta\left(\frac{|\left(\boldsymbol{\varepsilon}+1\right)\boldsymbol{\delta}_{3}|}{a_{0}}-1\right)}
\boldsymbol{\varepsilon}=\varepsilon\left(\begin{array}{cc}
\mathrm{cos}^{2}\theta-\rho\mathrm{sin^{2}\theta} & \left(1+\rho\right)\mathrm{cos}\theta\mathrm{sin}\theta\\
\left(1+\rho\right)\mathrm{cos}\theta\mathrm{sin}\theta & \mathrm{sin^{2}\theta}-\rho\mathrm{cos}^{2}\theta
\end{array}\right)
t_0 = 2.7\, \mathrm{eV}
\beta \approx 3
Technical details of the model
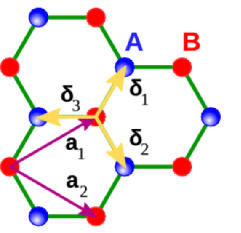
Tight-binding model for pristine graphene
In real space:
\left|\alpha,\underline{m}\right\rangle =\left|\alpha\right\rangle \left|\underline{m}\right\rangle ,\ \left|A\right\rangle =\left(\begin{array}{c}
1\\
0
\end{array}\right),\ \left|B\right\rangle =\left(\begin{array}{c}
0\\
1
\end{array}\right)
\hat{H}_\mathrm{Gr}=\sum_{\underline{m}} d_1\left|B,\underline{m}\right\rangle \left\langle A,\underline{m}\right|+ d_2\left|B,\underline{m}\right\rangle \left\langle A,\underline{m}+\boldsymbol{a}_1\right|
+ d_3\left|B,\underline{m}\right\rangle \left\langle A,\underline{m}+\boldsymbol{a}_2\right|+\text{h.c.}
\boldsymbol{R}_{\underline{m}}=m_{1}\boldsymbol{a}_{1}+m_{2}\boldsymbol{a}_{2}=\underline{m}\cdot\underline{\boldsymbol{a}}
Consider the Kekulé pattern as an ordered disorder
Technical details of the model
Kekulé perturbation operator
The periodicity is different!
\hat{H}_\mathrm{KeK} =\Delta\sum_{\underline{M}} d_{2} \left|B,\underline{M}\cdot \underline{\boldsymbol{A}}\right\rangle \left\langle A,\underline{M}\cdot \underline{\boldsymbol{A}}+\boldsymbol{a}_{2}\right| \\
+ d_{3}\left|B,\underline{M}\cdot \underline{\boldsymbol{A}}\right\rangle \left\langle A,\underline{M}\cdot \underline{\boldsymbol{A}}+\boldsymbol{a}_{1}\right| \\
+d_{1}\left|B,\underline{M}\cdot \underline{\boldsymbol{A}}+\boldsymbol{a}_{1}\right\rangle \left\langle A,\underline{M}\cdot \underline{\boldsymbol{A}}+\boldsymbol{a}_{1}\right|\\
+d_{1}\left|B,\underline{M}\cdot \underline{\boldsymbol{A}}+\boldsymbol{a}_{2}\right\rangle \left\langle A,\underline{M}\cdot \underline{\boldsymbol{A}}+\boldsymbol{a}_{2}\right| \\
+d_{2}\left|B,\underline{M}\cdot \underline{\boldsymbol{A}}+\boldsymbol{a}_{1}\right\rangle \left\langle A,\underline{M}\cdot \underline{\boldsymbol{A}}+\boldsymbol{a}_{2}+\boldsymbol{a}_{1}\right|\\
+d_{3}\left|B,\underline{M}\cdot \underline{\boldsymbol{A}}+\boldsymbol{a}_{2}\right\rangle \left\langle A,\underline{M}\cdot \underline{\boldsymbol{A}}+\boldsymbol{a}_{2}+\boldsymbol{a}_{1}\right|
+\text{h.c.}
In real space:
\mathbf{A}_{1}=2\mathbf{a}_{1}-\mathbf{a}_{2}\qquad\mathbf{A}_{2}=-\mathbf{a}_{1}+2\mathbf{a}_{2}.
Technical details of the model
Kene-Male perturbation operator
The periodicity is different!
\hat{H}_\mathrm{SOI}=\frac{im}{\sqrt{3}}\sum_{\underline{M}}\left(d_{4}\left|B,\underline{M}\cdot \underline{\boldsymbol{A}}\right\rangle \left\langle B,\underline{M}\cdot \underline{\boldsymbol{A}}+\boldsymbol{a}_{1}\right|+\right. \\
d_{6}\left|B,\underline{M} \underline{\boldsymbol{A}}+\boldsymbol{a}_{1}\right\rangle \left\langle B,\underline{M}\cdot \underline{\boldsymbol{A}}+\boldsymbol{a}_{2}\right|+ \\
d_{5}\left|B,\underline{M}\cdot \underline{\boldsymbol{A}}+\boldsymbol{a}_{2}\right\rangle \left\langle B,\underline{M}\cdot \underline{\boldsymbol{A}}\right|+\\
d_{5}\left|A,\underline{M}\cdot \underline{\boldsymbol{A}}+\boldsymbol{a}_{1}\right\rangle \left\langle A,\underline{M}\cdot \underline{\boldsymbol{A}}+\boldsymbol{a}_{1}+\boldsymbol{a}_{2}\right|+ \\
d_{4}\left|A,\underline{M}\cdot \underline{\boldsymbol{A}}+\boldsymbol{a}_{1}+\boldsymbol{a}_{2}\right\rangle \left\langle A,\underline{M}\cdot \underline{\boldsymbol{A}}+\boldsymbol{a}_{2}\right|+ \\
\left.d_{6}\left|A,\underline{M}\cdot \underline{\boldsymbol{A}}+\boldsymbol{a}_{2}\right\rangle \left\langle A,\underline{M}\cdot \underline{\boldsymbol{A}}+\boldsymbol{a}_{1}\right|\right)+\text{h.c.}.
In real space:
\mathbf{A}_{1}=2\mathbf{a}_{1}-\mathbf{a}_{2}\qquad\mathbf{A}_{2}=-\mathbf{a}_{1}+2\mathbf{a}_{2}.
Technical details of the model
The full tight-binding Hamiltonian:
\hat{H}=\hat{H}_\mathrm{Gr}+\hat{H}_\mathrm{Kek}+\hat{H}_\mathrm{SOI}
\hat{H}_\mathrm{Gr}=\sum_{\underline{m}} d_1\left|B,\underline{m}\right\rangle \left\langle A,\underline{m}\right| \\
+ d_2\left|B,\underline{m}\right\rangle \left\langle A,\underline{m}+\boldsymbol{a}_1\right| \\
+ d_3\left|B,\underline{m}\right\rangle \left\langle A,\underline{m}+\boldsymbol{a}_2\right|+\text{h.c.}
\hat{H}_\mathrm{KeK} =\Delta\sum_{\underline{M}} d_{2} \left|B,\underline{M}\cdot \underline{\boldsymbol{A}}\right\rangle \left\langle A,\underline{M}\cdot \underline{\boldsymbol{A}}+\boldsymbol{a}_{2}\right| \\
+ d_{3}\left|B,\underline{M}\cdot \underline{\boldsymbol{A}}\right\rangle \left\langle A,\underline{M}\cdot \underline{\boldsymbol{A}}+\boldsymbol{a}_{1}\right| \\
+d_{1}\left|B,\underline{M}\cdot \underline{\boldsymbol{A}}+\boldsymbol{a}_{1}\right\rangle \left\langle A,\underline{M}\cdot \underline{\boldsymbol{A}}+\boldsymbol{a}_{1}\right|\\
+d_{1}\left|B,\underline{M}\cdot \underline{\boldsymbol{A}}+\boldsymbol{a}_{2}\right\rangle \left\langle A,\underline{M}\cdot \underline{\boldsymbol{A}}+\boldsymbol{a}_{2}\right| \\
+d_{2}\left|B,\underline{M}\cdot \underline{\boldsymbol{A}}+\boldsymbol{a}_{1}\right\rangle \left\langle A,\underline{M}\cdot \underline{\boldsymbol{A}}+\boldsymbol{a}_{2}+\boldsymbol{a}_{1}\right|\\
+d_{3}\left|B,\underline{M}\cdot \underline{\boldsymbol{A}}+\boldsymbol{a}_{2}\right\rangle \left\langle A,\underline{M}\cdot \underline{\boldsymbol{A}}+\boldsymbol{a}_{2}+\boldsymbol{a}_{1}\right|
+\text{h.c.}
\hat{H}_\mathrm{SOI}=\frac{im}{\sqrt{3}}\sum_{\underline{M}}\left(d_{4}\left|B,\underline{M}\cdot \underline{\boldsymbol{A}}\right\rangle \left\langle B,\underline{M}\cdot \underline{\boldsymbol{A}}+\boldsymbol{a}_{1}\right|+\right. \\
d_{6}\left|B,\underline{M} \underline{\boldsymbol{A}}+\boldsymbol{a}_{1}\right\rangle \left\langle B,\underline{M}\cdot \underline{\boldsymbol{A}}+\boldsymbol{a}_{2}\right|+ \\
d_{5}\left|B,\underline{M}\cdot \underline{\boldsymbol{A}}+\boldsymbol{a}_{2}\right\rangle \left\langle B,\underline{M}\cdot \underline{\boldsymbol{A}}\right|+\\
d_{5}\left|A,\underline{M}\cdot \underline{\boldsymbol{A}}+\boldsymbol{a}_{1}\right\rangle \left\langle A,\underline{M}\cdot \underline{\boldsymbol{A}}+\boldsymbol{a}_{1}+\boldsymbol{a}_{2}\right|+ \\
d_{4}\left|A,\underline{M}\cdot \underline{\boldsymbol{A}}+\boldsymbol{a}_{1}+\boldsymbol{a}_{2}\right\rangle \left\langle A,\underline{M}\cdot \underline{\boldsymbol{A}}+\boldsymbol{a}_{2}\right|+ \\
\left.d_{6}\left|A,\underline{M}\cdot \underline{\boldsymbol{A}}+\boldsymbol{a}_{2}\right\rangle \left\langle A,\underline{M}\cdot \underline{\boldsymbol{A}}+\boldsymbol{a}_{1}\right|\right)+\text{h.c.}.
Technical details of the model
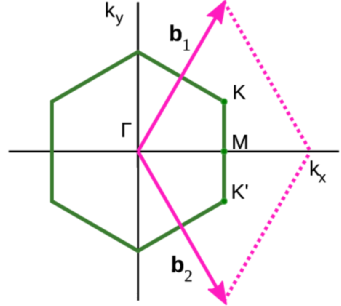
Dispersion relation \( \rightarrow \) Fourier-transformation
\left|B,\underline{m}\right\rangle =\frac{1}{\sqrt{N}}\sum_{\boldsymbol{k}}\mathrm{e}^{i\boldsymbol{k}\boldsymbol{R_{\underline{m}}}}\left|B,\boldsymbol{k}\right\rangle, \\
\left|A,\underline{m}\right\rangle =\frac{1}{\sqrt{N}}\sum_{\boldsymbol{k}}\mathrm{e}^{i\boldsymbol{k}\left(\boldsymbol{R_{\underline{m}}}+\boldsymbol{\delta}_{1}\right)}\left|A,\boldsymbol{k}\right\rangle
Fourier-transformation is tricky...
\boldsymbol{K}_{\pm}=\frac{2\boldsymbol{b}_{1}+\boldsymbol{b}_{2}}{3},\frac{2\boldsymbol{b}_{2}+\boldsymbol{b}_{1}}{3}\\
\mathbf{G}=\boldsymbol{K}_{+}-\boldsymbol{K}_{-}=\frac{\mathbf{b}_{1}-\mathbf{b}_{2}}{3}
Technical details of the model
\sum_{\boldsymbol{k},\boldsymbol{k}'}\sum_{m_{1},m_{2}}\left|B,\boldsymbol{k}\right\rangle \left\langle A,\boldsymbol{k}'\right|\mathrm{e}^{-i\left(\boldsymbol{k}'-\boldsymbol{k}\right)\left(m_{1}\left(2\boldsymbol{a}_{1}-\boldsymbol{a}_{2}\right)+m_{2}\left(2\boldsymbol{a}_{2}-\boldsymbol{a}_{1}\right)\right)}=
\sum_{\boldsymbol{k},\boldsymbol{k}'}\left|B,\boldsymbol{k}\right\rangle \left\langle A,\boldsymbol{k}'\right|\frac{1}{3}\left(\delta_{\boldsymbol{k}\boldsymbol{k}'}+\delta_{\boldsymbol{k}\boldsymbol{k}'+\boldsymbol{G}}+\delta_{\boldsymbol{k}\boldsymbol{k}'-\boldsymbol{G}}\right)
Technical details of the model
After the FT
\hat{H}(\boldsymbol{k})=\underline{\Psi}_{\boldsymbol{k}}^{\dagger}\left(\begin{matrix}
\boldsymbol{\Omega} & \boldsymbol{\Gamma} \\
\boldsymbol{\Gamma}^\dagger & -\boldsymbol{\Omega}^\dagger \\
\end{matrix} \right)\underline{\Psi}_{\boldsymbol{k}}
\underline{\Psi}_{\boldsymbol{k}}=\left(\begin{array}{cccccc}
\left|B,\boldsymbol{k}\right\rangle & \left|B,\boldsymbol{k}+\boldsymbol{G}\right\rangle & \left|B,\boldsymbol{k}-\boldsymbol{G}\right\rangle & \left|A,\boldsymbol{k}\right\rangle & \left|A,\boldsymbol{k}+\boldsymbol{G}\right\rangle & \left|A,\boldsymbol{k}-\boldsymbol{G}\right\rangle \end{array}\right)
\( \boldsymbol{\Omega} \) and \( \boldsymbol{\Gamma} \) are ugly \( 3\times3 \) matrices.
Identify low-energy part:
\Psi_\boldsymbol{k}=\left(-\left| A, \boldsymbol{k}+ \boldsymbol{G} \right. \rangle \left|B,\boldsymbol{k}-G\right.\rangle \left|B,\boldsymbol{k}+G\right.\rangle \left|A,\boldsymbol{k}+G\right.\rangle \right)
Taylor expansion, momentum and strain are the small parameters
Technical details of the model
Taylor expansion, momentum and strain are the small parameters, where to expand?
G. G. Naumis et. al. PRB, vol. 99, no. 3, 035411, 2019
\mathbf{K}_D = \pm \left( \mathbf{G} + \mathbf{A} \right)
F. Guinea, et. al. Physics Reports,vol. 496, no. 109148, 2010.
A_x = \frac{\beta}{2a_{cc}}\left( \epsilon_{xx} - \epsilon_{yy} \right) \\
A_y = -\frac{\beta}{a_{cc}} \epsilon_{xy}
Technical details of the model
The low-energy Hamiltonian
\hat{H}\left(\boldsymbol{k}\right)=-\frac{3}{2}t\left(1+\frac{2\Delta}{3}\right)\left[\boldsymbol{\sigma}\boldsymbol{A}\otimes\tau_{z}+\boldsymbol{\sigma}\left(\boldsymbol{1}+\left(1-\beta\right)\boldsymbol{\varepsilon}\right)\boldsymbol{k}\otimes\tau_{0}\right]-\\[0.5em]
\frac{t\Delta}{2}\left[\left(\beta\mathrm{Sp}\left(\boldsymbol{\varepsilon}\right)-2\right)\sigma_{z}\otimes\tau_{x}+(\boldsymbol{A}\times\boldsymbol{k})_{z}\sigma_{0}\otimes\tau_{y}+\boldsymbol{A}\boldsymbol{k}\sigma_{0}\otimes\tau_{x}\right]+\\[0.5em]
m\left[\boldsymbol{A}\boldsymbol{k}\sigma_{z}\otimes\tau_{z}-\left(\frac{1}{2}\beta\mathrm{Tr}\left(\varepsilon\right)-1\right)\sigma_{z}\otimes\tau_{0}\right]-\\[0.5em]
m\left[\left(\begin{array}{cc}
(\boldsymbol{M}\boldsymbol{k})_{x}-i(\boldsymbol{M}\boldsymbol{k})_{y}\\[0.5em]
(\boldsymbol{M}^{*}\boldsymbol{k})_{x}+i(\boldsymbol{M}^{*}\boldsymbol{k})_{y}
\end{array}\right)+\left[\left(1+\boldsymbol{\varepsilon}\right)\boldsymbol{k}\right]\boldsymbol{\sigma}\right]\otimes\tau_{x},
\boldsymbol{A}=\frac{\beta}{2a_{0}}\varepsilon\left(1+\rho\right)\left(\begin{matrix}
\cos^2\vartheta\\
-\sin^2\vartheta
\end{matrix}\right)
\Psi_\boldsymbol{k}=\left(-\left| A, \boldsymbol{k}+ \boldsymbol{G} \right. \rangle \left|B,\boldsymbol{k}-G\right.\rangle \left|B,\boldsymbol{k}+G\right.\rangle \left|A,\boldsymbol{k}+G\right.\rangle \right)
\begin{array}{c}
\hat{H}=-v\left(
{\boldsymbol{k}}\cdot\boldsymbol{\sigma}\otimes\tau_{0}
+\boldsymbol{A}\cdot\boldsymbol{\sigma}\otimes\tau_{z}
\right)\\
+\Delta\sigma_z\otimes\tau_x
-m\sigma_z\otimes\tau_0
\end{array}
\boldsymbol{A}=\underbrace{\frac{\beta}{2a_{0}}\varepsilon\left(1+\rho\right)}\left(\begin{array}{r}
\cos2\vartheta\\
-\sin2\vartheta
\end{array}\right)
|\xi|=\sqrt{\Delta^2-m^2}
\xi/v
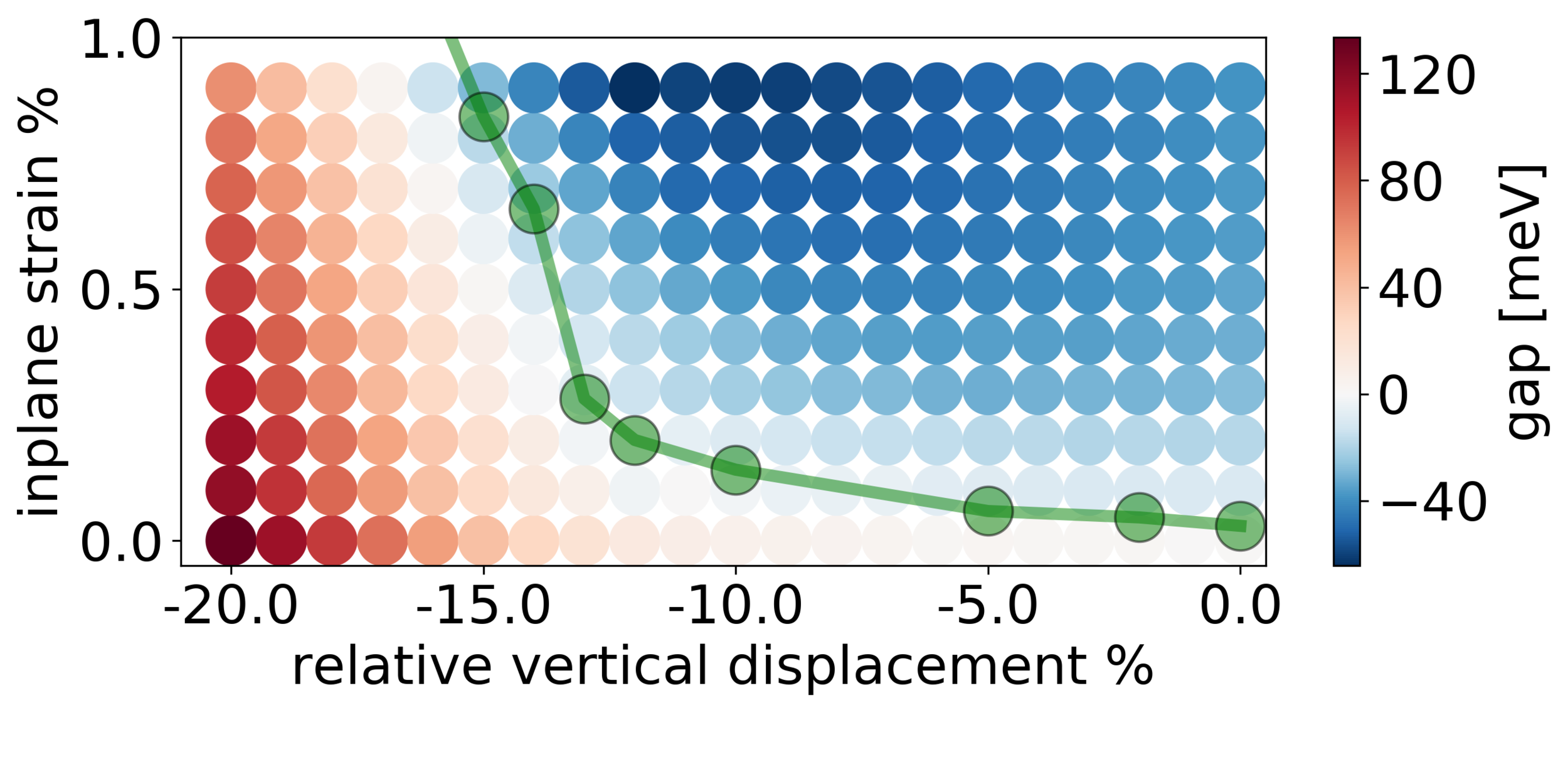
Strain can close the gap at \(\boldsymbol{k}=\boldsymbol{0}\) if
Minimal model
Gamayun et al. New J. Phys. 20, 023016 (2018)
Z. Tajkov et. al. Physical Review B 101 (23), 235146 (2020)
\Psi_\boldsymbol{k}=\left(-\left| A, \boldsymbol{k}+ \boldsymbol{G} \right. \rangle \left|B,\boldsymbol{k}-G\right.\rangle \left|B,\boldsymbol{k}+G\right.\rangle \left|A,\boldsymbol{k}+G\right.\rangle \right)
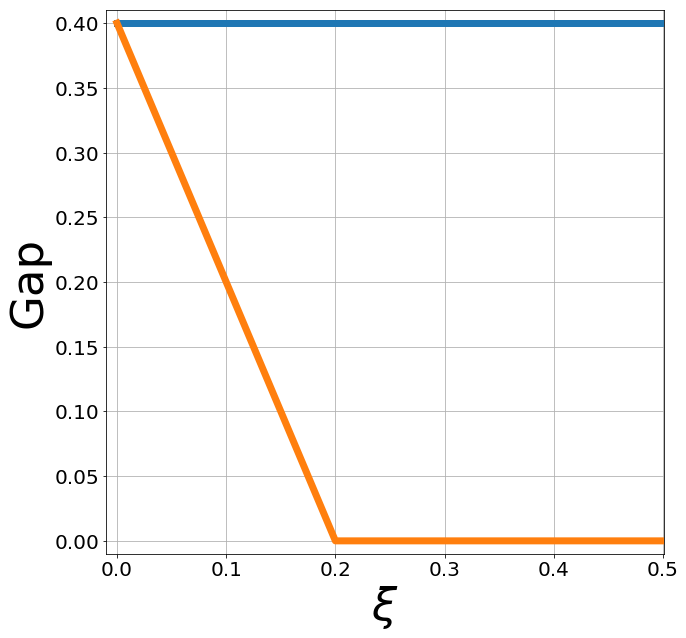
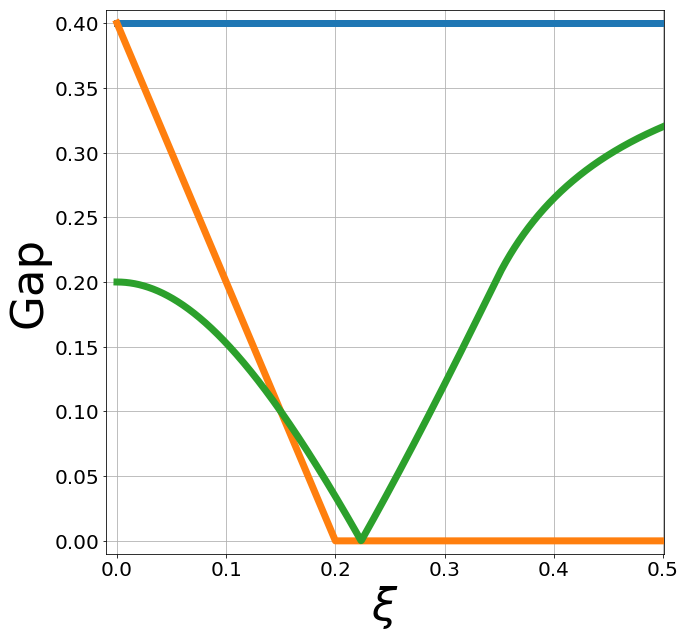
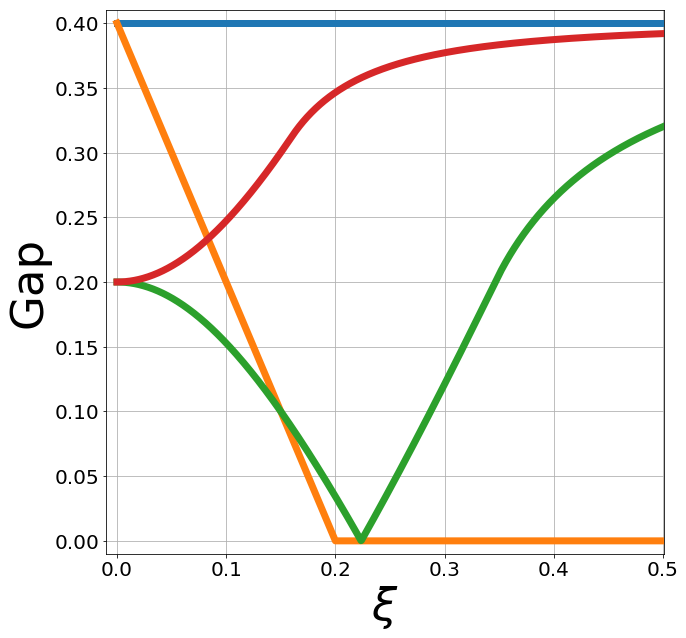
Strain kills Kekulé but KM gap is resilient!
\Delta=0; m=0.2
\Delta=0.2; m=0
\Delta = 0.2; m=0.1
\Delta = 0.1; m=0.2
The Team
László Oroszlány
János Koltai
József Cserti
Thanks!
Z. Tajkov et al. Nanoscale 11, 12704 (2019)
Z. Tajkov et al. Appl. Sci. 9, 4330 (2019)
Z. Tajkov et al. Physical Review B 101 (23), 235146 (2020)
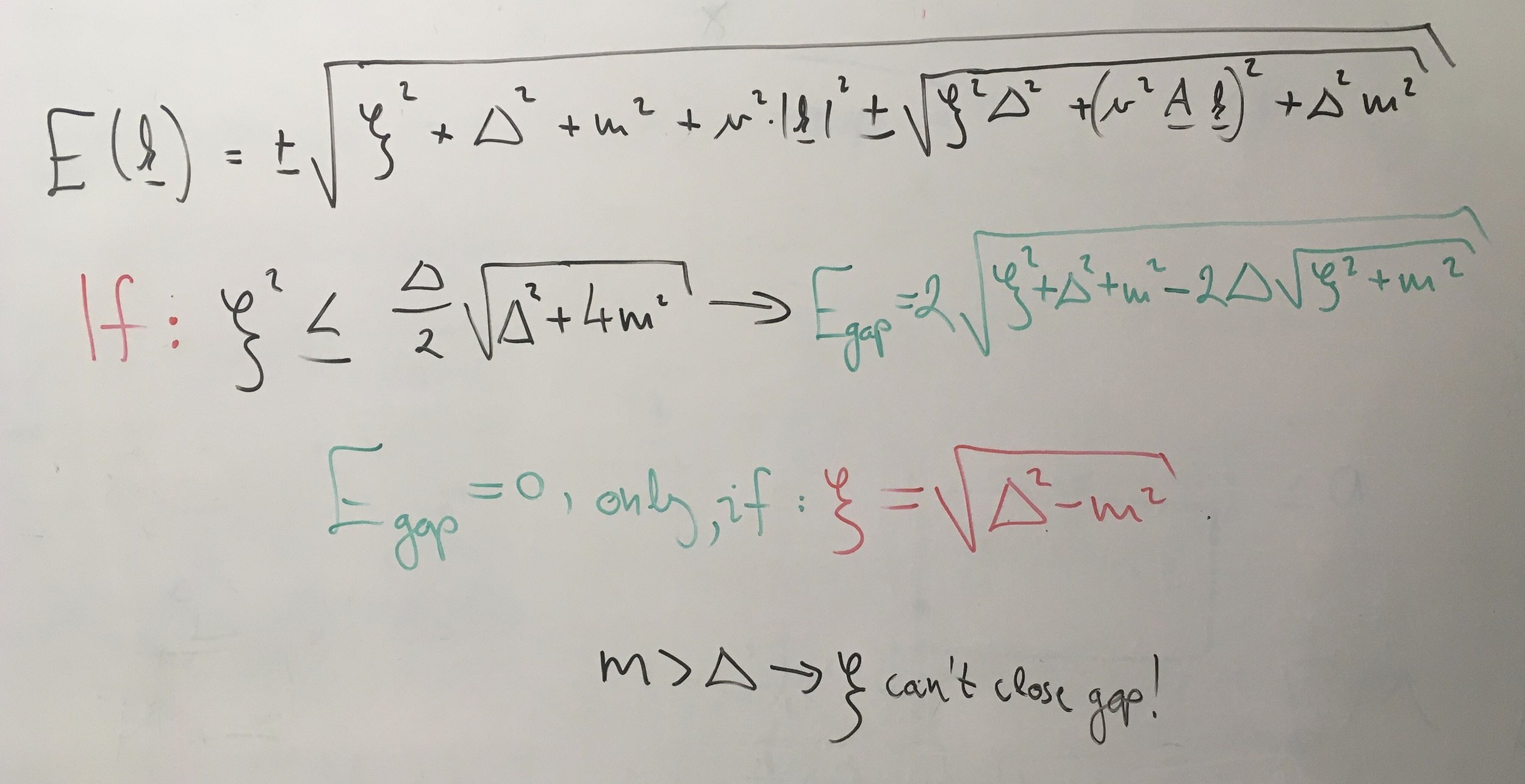
Competition of trivial and topological phases in graphene based hybrid systems - Regensburg
By novidad21
