Kétdimenziós Hibrid Nanorendszerek Elméleti Vizsgálata
Tajkov Zoltán
PhD hallgató doktori védése
Biológiai Fizika Tanszék, Eötvös Loránd Tudományegyetem
Témavezetők: Koltai János és Oroszlány László
Budapest, 2021. június 3.
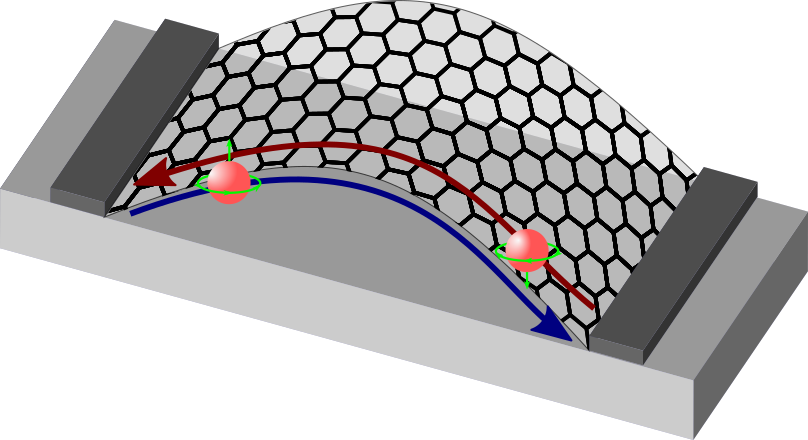
A grafén egy...
A. K. Geim, I. V. Grigorieva Nature 499, 419 (2013)
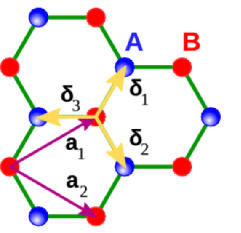
A grafén egy...
... remek alap!
A. K. Geim, I. V. Grigorieva Nature 499, 419 (2013)
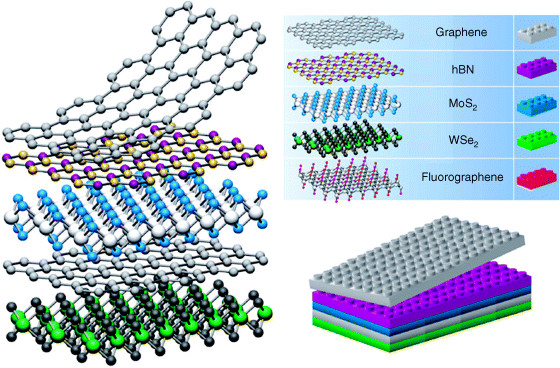
A grafén egy...
... remek alap!
A. K. Geim, I. V. Grigorieva Nature 499, 419 (2013)
Hogy lehet a grafénben topologikus tiltott sávot nyitni?
A grafén egy...
... remek alap!
C. L. Kane, E. J. Mele, PRL 95, 226801 (2005)
Hogy lehet a grafénben topologikus tiltott sávot nyitni?
SOC!!
J. Sichau et. al. PRL 122, 046403 (2019)
Milyen erős az effektus?
SOC!!
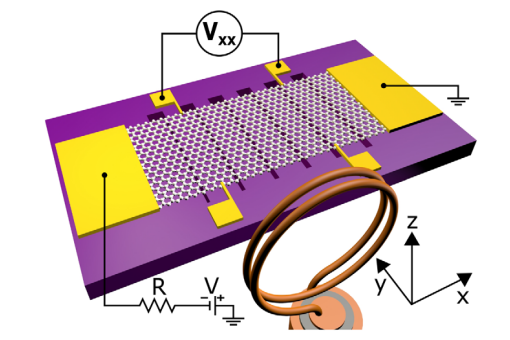
A spin-pálya kölcsönhatás a grafénben eredendően gyenge.
\Delta E_{\mathrm{SOI}}=\left( 42,2 \pm 0,8 \right) \mu \mathrm{eV}
BiTeX: óriási SOC
Ishizaka et al. Nature Materials 10, 521 (2011)
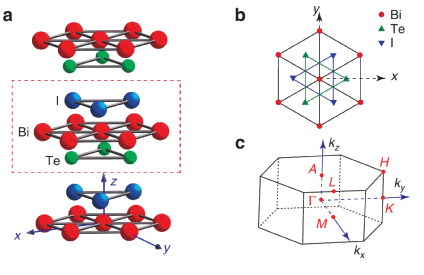
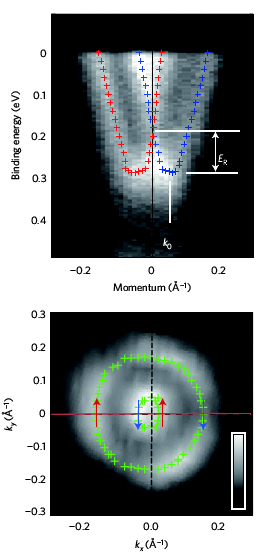
BiTeX egyréteg
Fülöp et al. 2D Mater. 5, 031013 (2018)
1. Tézispont
Fülöp et al. 2D Mater. 5, 031013 (2018)
Sűrűségfunkcionál-elméleten alapuló számolások segítségével vizsgáltam a BiTeI arany hordozóra történő exfóliálásának lehetőségét. Származtattam a kötési energiákat az arany hordozó és a BiTeI réteg, illetve a BiTeI rétegen belüli egységek között. A számítások alapján a BiTeI réteg jobban köt az arany felülethez, mint a saját tömbjéhez, de gyengébben, mint a BiTeI rétegben található kovalens kötések. Ebből következik, hogy a BiTeI exfóliálás során nagyobb valószínűséggel marad a hordozón, mint hogy szétszakadna. Meghatároztam a szabadon álló BiTeI és az arany hordozón levő BiTeI állapotsűrűségét, amelyből kiolvasható, hogy az eredetileg szigetelő BiTeI az arany hatására vezető lesz. Ezeket az elméleti számolásokat a Csonka Szabolcs által vezetett, BME-n működő kísérleti csoport kísérletileg is igazolta.
BiTeX/grafén heteroszerkezetek
BiTeI sandwich: Kou et al. ACS Nano, 8 10448 (2014)
BiTeX/grafén heteroszerkezetek
BiTeI sandwich: Kou et al. ACS Nano, 8 10448 (2014)
BiTeX/grafén heteroszerkezetek
BiTeI sandwich: Kou et al. ACS Nano, 8 10448 (2014)
BiTeCl és grafén heteroszerkezet fázisdiagramja
BiTeCl / BiTeBr grafén heteroszerkezet fázisdiagramja
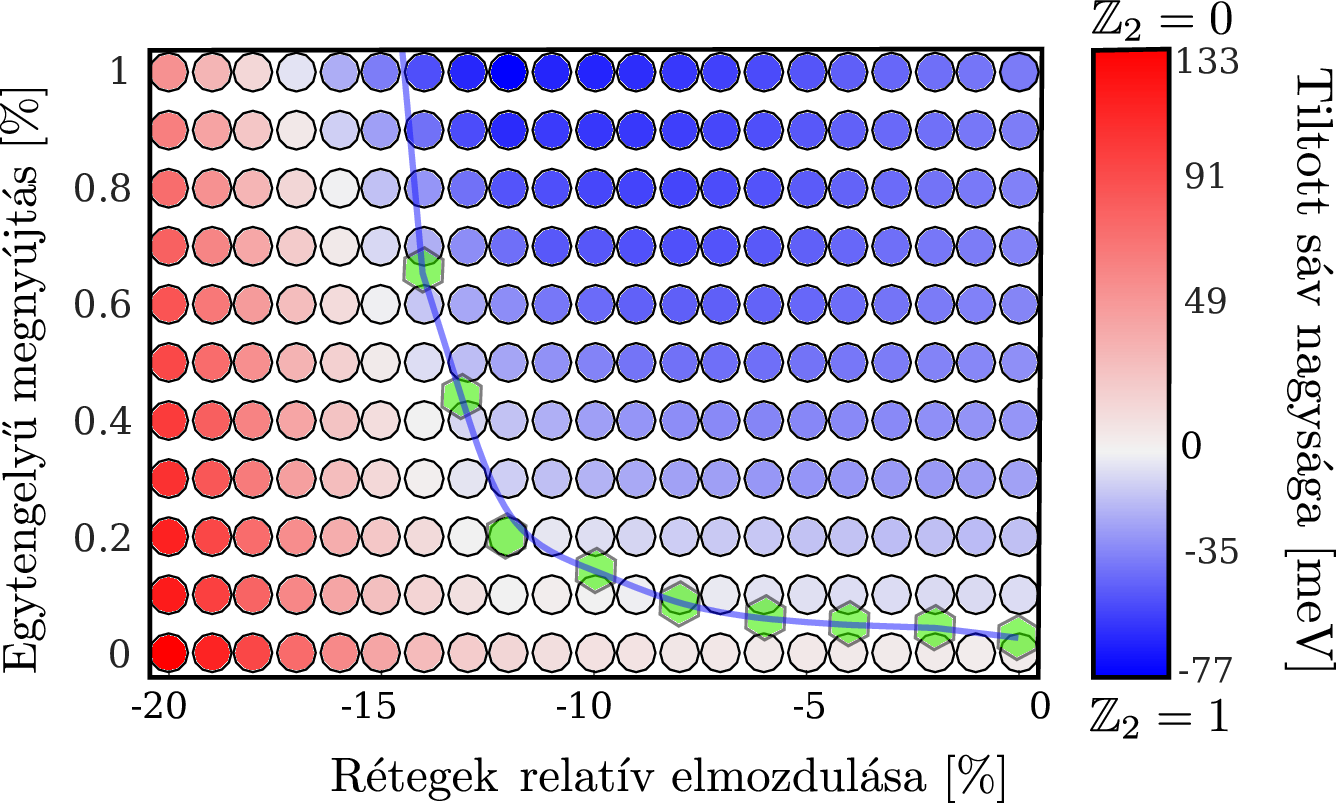
A grafén és BiTeX anyagcsalád összetételéből képzett heterostruktúrák elektromos tulajdonságait vizsgáltam sűrűségfunkcionálelméleten alapuló módszerekkel. Megmutattam, hogy a kísérletileg relevánsabb, egyoldalas grafén-BiTeX rendszer megőrzi a grafén félfém tulajdonságát egyensúlyi állapotban. Megvizsgáltam a nyomás és egytengelyű mechanikai deformáció hatását a heterostruktúrán és azt találtam, hogy rendszerben a kísérletileg elérhető < 1% nyújtás hatására számottevő topologikus tiltott sáv nyílik. Egy, a sűrűségfunkcionál-elméleten alapuló számításokhoz illesztett soros kötésű modell segítségével sikerült a fázishatárokat reprodukálni.
2. Tézispont
Mit szűrhetünk le a DFT eredményekből?
A két legfontosabb paraméter
Kekulé
Kane-Mele
Az egytengelyű nyújtás a topologikus tiltott sávot promótálja.
Technical details of the model
We have to deal with:
- Graphene
- Kekulé
- Kene-Male
- Strain
Divide et impera
Start with graphene + strain
\boldsymbol{a}_{2,1} =a_{\mathrm{cc}}\frac{1}{2}\left(\begin{array}{c}
\pm\sqrt{3}\\
3
\end{array}\right)
\boldsymbol{b}_{2,1} =\left(\begin{array}{c}
\pm\frac{2\sqrt{3}}{3a_{\mathrm{cc}}}\pi\\
\frac{2}{3a_{\mathrm{cc}}}\pi
\end{array}\right)
\boldsymbol{\delta}_{1}=\left(\begin{array}{c}
0\\
-1
\end{array}\right) \\
\boldsymbol{\delta}_{2}=\frac{1}{2}\left(\begin{array}{c}
\sqrt{3}\\
1
\end{array}\right)\\
\boldsymbol{\delta}_{3}=\frac{1}{2}\left(\begin{array}{c}
-\sqrt{3}\\
1
\end{array}\right) \\
d_{1}=t_{0}\mathrm{e}^{-\beta\left(\frac{|\left(\boldsymbol{\varepsilon}+1\right)\boldsymbol{\delta}_{1}|}{a_{0}}-1\right)} \\
d_{2}=t_{0}\mathrm{e}^{-\beta\left(\frac{|\left(\boldsymbol{\varepsilon}+1\right)\boldsymbol{\delta}_{2}|}{a_{0}}-1\right)} \\
d_{3}=t_{0}\mathrm{e}^{-\beta\left(\frac{|\left(\boldsymbol{\varepsilon}+1\right)\boldsymbol{\delta}_{3}|}{a_{0}}-1\right)}
\boldsymbol{\varepsilon}=\varepsilon\left(\begin{array}{cc}
\mathrm{cos}^{2}\theta-\rho\mathrm{sin^{2}\theta} & \left(1+\rho\right)\mathrm{cos}\theta\mathrm{sin}\theta\\
\left(1+\rho\right)\mathrm{cos}\theta\mathrm{sin}\theta & \mathrm{sin^{2}\theta}-\rho\mathrm{cos}^{2}\theta
\end{array}\right)
t_0 = 2.7\, \mathrm{eV}
\beta \approx 3
Technical details of the model
Tight-binding model for pristine graphene
In real space:
\left|\alpha,\underline{m}\right\rangle =\left|\alpha\right\rangle \left|\underline{m}\right\rangle ,\ \left|A\right\rangle =\left(\begin{array}{c}
1\\
0
\end{array}\right),\ \left|B\right\rangle =\left(\begin{array}{c}
0\\
1
\end{array}\right)
\hat{H}_\mathrm{Gr}=\sum_{\underline{m}} d_1\left|B,\underline{m}\right\rangle \left\langle A,\underline{m}\right|+ d_2\left|B,\underline{m}\right\rangle \left\langle A,\underline{m}+\boldsymbol{a}_1\right|
+ d_3\left|B,\underline{m}\right\rangle \left\langle A,\underline{m}+\boldsymbol{a}_2\right|+\text{h.c.}
\boldsymbol{R}_{\underline{m}}=m_{1}\boldsymbol{a}_{1}+m_{2}\boldsymbol{a}_{2}=\underline{m}\cdot\underline{\boldsymbol{a}}
Consider the Kekulé pattern as an ordered disorder
Technical details of the model
Kekulé perturbation operator
The periodicity is different!
\hat{H}_\mathrm{KeK} =\Delta\sum_{\underline{M}} d_{2} \left|B,\underline{M}\cdot \underline{\boldsymbol{A}}\right\rangle \left\langle A,\underline{M}\cdot \underline{\boldsymbol{A}}+\boldsymbol{a}_{2}\right| \\
+ d_{3}\left|B,\underline{M}\cdot \underline{\boldsymbol{A}}\right\rangle \left\langle A,\underline{M}\cdot \underline{\boldsymbol{A}}+\boldsymbol{a}_{1}\right| \\
+d_{1}\left|B,\underline{M}\cdot \underline{\boldsymbol{A}}+\boldsymbol{a}_{1}\right\rangle \left\langle A,\underline{M}\cdot \underline{\boldsymbol{A}}+\boldsymbol{a}_{1}\right|\\
+d_{1}\left|B,\underline{M}\cdot \underline{\boldsymbol{A}}+\boldsymbol{a}_{2}\right\rangle \left\langle A,\underline{M}\cdot \underline{\boldsymbol{A}}+\boldsymbol{a}_{2}\right| \\
+d_{2}\left|B,\underline{M}\cdot \underline{\boldsymbol{A}}+\boldsymbol{a}_{1}\right\rangle \left\langle A,\underline{M}\cdot \underline{\boldsymbol{A}}+\boldsymbol{a}_{2}+\boldsymbol{a}_{1}\right|\\
+d_{3}\left|B,\underline{M}\cdot \underline{\boldsymbol{A}}+\boldsymbol{a}_{2}\right\rangle \left\langle A,\underline{M}\cdot \underline{\boldsymbol{A}}+\boldsymbol{a}_{2}+\boldsymbol{a}_{1}\right|
+\text{h.c.}
In real space:
\mathbf{A}_{1}=2\mathbf{a}_{1}-\mathbf{a}_{2}\qquad\mathbf{A}_{2}=-\mathbf{a}_{1}+2\mathbf{a}_{2}.
Technical details of the model
Kene-Male perturbation operator
The periodicity is different!
\hat{H}_\mathrm{SOI}=\frac{im}{\sqrt{3}}\sum_{\underline{M}}\left(d_{4}\left|B,\underline{M}\cdot \underline{\boldsymbol{A}}\right\rangle \left\langle B,\underline{M}\cdot \underline{\boldsymbol{A}}+\boldsymbol{a}_{1}\right|+\right. \\
d_{6}\left|B,\underline{M} \underline{\boldsymbol{A}}+\boldsymbol{a}_{1}\right\rangle \left\langle B,\underline{M}\cdot \underline{\boldsymbol{A}}+\boldsymbol{a}_{2}\right|+ \\
d_{5}\left|B,\underline{M}\cdot \underline{\boldsymbol{A}}+\boldsymbol{a}_{2}\right\rangle \left\langle B,\underline{M}\cdot \underline{\boldsymbol{A}}\right|+\\
d_{5}\left|A,\underline{M}\cdot \underline{\boldsymbol{A}}+\boldsymbol{a}_{1}\right\rangle \left\langle A,\underline{M}\cdot \underline{\boldsymbol{A}}+\boldsymbol{a}_{1}+\boldsymbol{a}_{2}\right|+ \\
d_{4}\left|A,\underline{M}\cdot \underline{\boldsymbol{A}}+\boldsymbol{a}_{1}+\boldsymbol{a}_{2}\right\rangle \left\langle A,\underline{M}\cdot \underline{\boldsymbol{A}}+\boldsymbol{a}_{2}\right|+ \\
\left.d_{6}\left|A,\underline{M}\cdot \underline{\boldsymbol{A}}+\boldsymbol{a}_{2}\right\rangle \left\langle A,\underline{M}\cdot \underline{\boldsymbol{A}}+\boldsymbol{a}_{1}\right|\right)+\text{h.c.}.
In real space:
\mathbf{A}_{1}=2\mathbf{a}_{1}-\mathbf{a}_{2}\qquad\mathbf{A}_{2}=-\mathbf{a}_{1}+2\mathbf{a}_{2}.
Technical details of the model
The full tight-binding Hamiltonian:
\hat{H}=\hat{H}_\mathrm{Gr}+\hat{H}_\mathrm{Kek}+\hat{H}_\mathrm{SOI}
\hat{H}_\mathrm{Gr}=\sum_{\underline{m}} d_1\left|B,\underline{m}\right\rangle \left\langle A,\underline{m}\right| \\
+ d_2\left|B,\underline{m}\right\rangle \left\langle A,\underline{m}+\boldsymbol{a}_1\right| \\
+ d_3\left|B,\underline{m}\right\rangle \left\langle A,\underline{m}+\boldsymbol{a}_2\right|+\text{h.c.}
\hat{H}_\mathrm{KeK} =\Delta\sum_{\underline{M}} d_{2} \left|B,\underline{M}\cdot \underline{\boldsymbol{A}}\right\rangle \left\langle A,\underline{M}\cdot \underline{\boldsymbol{A}}+\boldsymbol{a}_{2}\right| \\
+ d_{3}\left|B,\underline{M}\cdot \underline{\boldsymbol{A}}\right\rangle \left\langle A,\underline{M}\cdot \underline{\boldsymbol{A}}+\boldsymbol{a}_{1}\right| \\
+d_{1}\left|B,\underline{M}\cdot \underline{\boldsymbol{A}}+\boldsymbol{a}_{1}\right\rangle \left\langle A,\underline{M}\cdot \underline{\boldsymbol{A}}+\boldsymbol{a}_{1}\right|\\
+d_{1}\left|B,\underline{M}\cdot \underline{\boldsymbol{A}}+\boldsymbol{a}_{2}\right\rangle \left\langle A,\underline{M}\cdot \underline{\boldsymbol{A}}+\boldsymbol{a}_{2}\right| \\
+d_{2}\left|B,\underline{M}\cdot \underline{\boldsymbol{A}}+\boldsymbol{a}_{1}\right\rangle \left\langle A,\underline{M}\cdot \underline{\boldsymbol{A}}+\boldsymbol{a}_{2}+\boldsymbol{a}_{1}\right|\\
+d_{3}\left|B,\underline{M}\cdot \underline{\boldsymbol{A}}+\boldsymbol{a}_{2}\right\rangle \left\langle A,\underline{M}\cdot \underline{\boldsymbol{A}}+\boldsymbol{a}_{2}+\boldsymbol{a}_{1}\right|
+\text{h.c.}
\hat{H}_\mathrm{SOI}=\frac{im}{\sqrt{3}}\sum_{\underline{M}}\left(d_{4}\left|B,\underline{M}\cdot \underline{\boldsymbol{A}}\right\rangle \left\langle B,\underline{M}\cdot \underline{\boldsymbol{A}}+\boldsymbol{a}_{1}\right|+\right. \\
d_{6}\left|B,\underline{M} \underline{\boldsymbol{A}}+\boldsymbol{a}_{1}\right\rangle \left\langle B,\underline{M}\cdot \underline{\boldsymbol{A}}+\boldsymbol{a}_{2}\right|+ \\
d_{5}\left|B,\underline{M}\cdot \underline{\boldsymbol{A}}+\boldsymbol{a}_{2}\right\rangle \left\langle B,\underline{M}\cdot \underline{\boldsymbol{A}}\right|+\\
d_{5}\left|A,\underline{M}\cdot \underline{\boldsymbol{A}}+\boldsymbol{a}_{1}\right\rangle \left\langle A,\underline{M}\cdot \underline{\boldsymbol{A}}+\boldsymbol{a}_{1}+\boldsymbol{a}_{2}\right|+ \\
d_{4}\left|A,\underline{M}\cdot \underline{\boldsymbol{A}}+\boldsymbol{a}_{1}+\boldsymbol{a}_{2}\right\rangle \left\langle A,\underline{M}\cdot \underline{\boldsymbol{A}}+\boldsymbol{a}_{2}\right|+ \\
\left.d_{6}\left|A,\underline{M}\cdot \underline{\boldsymbol{A}}+\boldsymbol{a}_{2}\right\rangle \left\langle A,\underline{M}\cdot \underline{\boldsymbol{A}}+\boldsymbol{a}_{1}\right|\right)+\text{h.c.}.
Technical details of the model
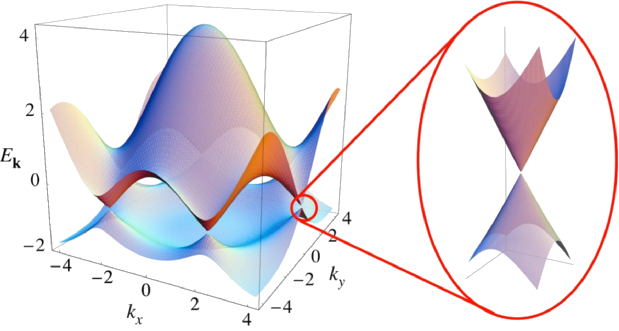
Dispersion relation \( \rightarrow \) Fourier-transformation
\left|B,\underline{m}\right\rangle =\frac{1}{\sqrt{N}}\sum_{\boldsymbol{k}}\mathrm{e}^{i\boldsymbol{k}\boldsymbol{R_{\underline{m}}}}\left|B,\boldsymbol{k}\right\rangle, \\
\left|A,\underline{m}\right\rangle =\frac{1}{\sqrt{N}}\sum_{\boldsymbol{k}}\mathrm{e}^{i\boldsymbol{k}\left(\boldsymbol{R_{\underline{m}}}+\boldsymbol{\delta}_{1}\right)}\left|A,\boldsymbol{k}\right\rangle
Fourier-transformation is tricky...
\boldsymbol{K}_{\pm}=\frac{2\boldsymbol{b}_{1}+\boldsymbol{b}_{2}}{3},\frac{2\boldsymbol{b}_{2}+\boldsymbol{b}_{1}}{3}\\
\mathbf{G}=\boldsymbol{K}_{+}-\boldsymbol{K}_{-}=\frac{\mathbf{b}_{1}-\mathbf{b}_{2}}{3}
Technical details of the model
\sum_{\boldsymbol{k},\boldsymbol{k}'}\sum_{m_{1},m_{2}}\left|B,\boldsymbol{k}\right\rangle \left\langle A,\boldsymbol{k}'\right|\mathrm{e}^{-i\left(\boldsymbol{k}'-\boldsymbol{k}\right)\left(m_{1}\left(2\boldsymbol{a}_{1}-\boldsymbol{a}_{2}\right)+m_{2}\left(2\boldsymbol{a}_{2}-\boldsymbol{a}_{1}\right)\right)}=
\sum_{\boldsymbol{k},\boldsymbol{k}'}\left|B,\boldsymbol{k}\right\rangle \left\langle A,\boldsymbol{k}'\right|\frac{1}{3}\left(\delta_{\boldsymbol{k}\boldsymbol{k}'}+\delta_{\boldsymbol{k}\boldsymbol{k}'+\boldsymbol{G}}+\delta_{\boldsymbol{k}\boldsymbol{k}'-\boldsymbol{G}}\right)
Technical details of the model
After the FT
\hat{H}(\boldsymbol{k})=\underline{\Psi}_{\boldsymbol{k}}^{\dagger}\left(\begin{matrix}
\boldsymbol{\Omega} & \boldsymbol{\Gamma} \\
\boldsymbol{\Gamma}^\dagger & -\boldsymbol{\Omega}^\dagger \\
\end{matrix} \right)\underline{\Psi}_{\boldsymbol{k}}
\underline{\Psi}_{\boldsymbol{k}}=\left(\begin{array}{cccccc}
\left|B,\boldsymbol{k}\right\rangle & \left|B,\boldsymbol{k}+\boldsymbol{G}\right\rangle & \left|B,\boldsymbol{k}-\boldsymbol{G}\right\rangle & \left|A,\boldsymbol{k}\right\rangle & \left|A,\boldsymbol{k}+\boldsymbol{G}\right\rangle & \left|A,\boldsymbol{k}-\boldsymbol{G}\right\rangle \end{array}\right)
\( \boldsymbol{\Omega} \) and \( \boldsymbol{\Gamma} \) are ugly \( 3\times3 \) matrices.
Identify low-energy part:
\Psi_\boldsymbol{k}=\left(-\left| A, \boldsymbol{k}+ \boldsymbol{G} \right. \rangle \left|B,\boldsymbol{k}-G\right.\rangle \left|B,\boldsymbol{k}+G\right.\rangle \left|A,\boldsymbol{k}+G\right.\rangle \right)
Taylor expansion, momentum and strain are the small parameters
Technical details of the model
Taylor expansion, momentum and strain are the small parameters, where to expand?
G. G. Naumis et. al. PRB, vol. 99, no. 3, 035411, 2019
\mathbf{K}_D = \pm \left( \mathbf{G} + \mathbf{A} \right)
F. Guinea, et. al. Physics Reports,vol. 496, no. 109148, 2010.
A_x = \frac{\beta}{2a_{cc}}\left( \epsilon_{xx} - \epsilon_{yy} \right) \\
A_y = -\frac{\beta}{a_{cc}} \epsilon_{xy}
Technical details of the model
The low-energy Hamiltonian
\hat{H}\left(\boldsymbol{k}\right)=-\frac{3}{2}t\left(1+\frac{2\Delta}{3}\right)\left[\boldsymbol{\sigma}\boldsymbol{A}\otimes\tau_{z}+\boldsymbol{\sigma}\left(\boldsymbol{1}+\left(1-\beta\right)\boldsymbol{\varepsilon}\right)\boldsymbol{k}\otimes\tau_{0}\right]-\\[0.5em]
\frac{t\Delta}{2}\left[\left(\beta\mathrm{Sp}\left(\boldsymbol{\varepsilon}\right)-2\right)\sigma_{z}\otimes\tau_{x}+(\boldsymbol{A}\times\boldsymbol{k})_{z}\sigma_{0}\otimes\tau_{y}+\boldsymbol{A}\boldsymbol{k}\sigma_{0}\otimes\tau_{x}\right]+\\[0.5em]
m\left[\boldsymbol{A}\boldsymbol{k}\sigma_{z}\otimes\tau_{z}-\left(\frac{1}{2}\beta\mathrm{Tr}\left(\varepsilon\right)-1\right)\sigma_{z}\otimes\tau_{0}\right]-\\[0.5em]
m\left[\left(\begin{array}{cc}
(\boldsymbol{M}\boldsymbol{k})_{x}-i(\boldsymbol{M}\boldsymbol{k})_{y}\\[0.5em]
(\boldsymbol{M}^{*}\boldsymbol{k})_{x}+i(\boldsymbol{M}^{*}\boldsymbol{k})_{y}
\end{array}\right)+\left[\left(1+\boldsymbol{\varepsilon}\right)\boldsymbol{k}\right]\boldsymbol{\sigma}\right]\otimes\tau_{x},
\boldsymbol{A}=\frac{\beta}{2a_{0}}\varepsilon\left(1+\rho\right)\left(\begin{matrix}
\cos^2\vartheta\\
-\sin^2\vartheta
\end{matrix}\right)
\Psi_\boldsymbol{k}=\left(-\left| A, \boldsymbol{k}+ \boldsymbol{G} \right. \rangle \left|B,\boldsymbol{k}-G\right.\rangle \left|B,\boldsymbol{k}+G\right.\rangle \left|A,\boldsymbol{k}+G\right.\rangle \right)
\begin{array}{c}
\hat{H}=-v\left(
{\boldsymbol{k}}\cdot\boldsymbol{\sigma}\otimes\tau_{0}
+\boldsymbol{A}\cdot\boldsymbol{\sigma}\otimes\tau_{z}
\right)\\
+\Delta\sigma_z\otimes\tau_x
-m\sigma_z\otimes\tau_0
\end{array}
\boldsymbol{A}=\underbrace{\frac{\beta}{2a_{0}}\varepsilon\left(1+\rho\right)}\left(\begin{array}{r}
\cos2\vartheta\\
-\sin2\vartheta
\end{array}\right)
\xi/v
Alacsony energiás effektív modell
Gamayun et al. New J. Phys. 20, 023016 (2018)
Z. Tajkov et. al. Physical Review B 101 (23), 235146 (2020)
\Psi_\boldsymbol{k}=\left(-\left| A, \boldsymbol{k}+ \boldsymbol{G} \right. \rangle \left|B,\boldsymbol{k}-G\right.\rangle \left|B,\boldsymbol{k}+G\right.\rangle \left|A,\boldsymbol{k}+G\right.\rangle \right)
\begin{array}{c}
\hat{H}=-v\left(
{\boldsymbol{k}}\cdot\boldsymbol{\sigma}\otimes\tau_{0}
+\boldsymbol{A}\cdot\boldsymbol{\sigma}\otimes\tau_{z}
\right)\\
+\Delta\sigma_z\otimes\tau_x
-m\sigma_z\otimes\tau_0
\end{array}
Z. Tajkov et. al. Physical Review B 101 (23), 235146 (2020)
3. Tézispont
A sűrűségfunkcionálelméleten alapuló számítások eredményei alapján felépítettem egy, a mechanikai megnyújtás hatásait szisztematikusabban figyelembe vevő szoros kötésű közelítésen alapuló modellt a grafén--BiTeX heterostruktúrák elektromos tulajdonságainak leírására. A kapott modellt a diszperziós reláció minimumhelyei körül sorbafejtve és a lineáris tagokat megtartva jutottam el egy effektív, a grafén alacsony energiás szabadsági fokait jól leíró modellhez. Feltártam a rendszer topologikus fázisdiagramját. A releváns paraméterek (mechanikai feszültség nagysága, Kekulé-O kötésalternálás erőssége és spin-pálya csatolás nagysága) függvényében körbejártam a lehetséges tiltott sáv nyitó mechanizmusokat. Megállapítottam, hogy a Kekulé-torzítás és spin-pálya kölcsönhatás versenyében a mechanikai feszültség úgy jut szerephez, hogy a Kekulé-O járulékát csökkenti, míg a spin-pálya csatolást nem befolyásolja.
Köszönöm a figyelmet!
László Oroszlány
János Koltai
József Cserti
A csapat:
Válaszok a bírálói kérdésekre
Széchenyi Gábor kérdései.
1. Ahogy a 4.3 ábrán is látható a különböző szendvicsszerkezetek elektromos tulajdonságainak tárgyalása során döntő fontosságú a Fermi-energia értékének pontos meghatározása. Hogyan és milyen pontossággal történik a Fermi-energia meghatározása?
Az általunk vizsgált és a dolgozatban bemutatott anyagok és fázisok esetén minden esetben a tiltott sáv jelenléte volt a kérdés és annak topologikus invariánsa. A bemutatott, tiltott sávval nem rendelkező anyagok esetén a Fermi-energia helyzete a számunkra fontos tulajdonságok szempontjából nem volt releváns, csupán a tény, hogy az anyag nem szigetelő. Ezen okoknál fogva a Fermi-energia pontossága nem merült fel, mint vizsgálandó kérdés. A SIESTA programkód egy iteratív eljárással határozza meg a Fermi-szintet, mégpedig a következőképpen. A konvergáltatott egyrészecskés sűrűségmátrix segítségével meghatározza a legmagasabb és legalacsonyabb energiájú állapotot. Első lépésben a Fermi-szintet a két állapot számtani közepeként állapítja meg. Kiszámítja ezen energiapontig az állapotok számát. Attól függően, hogy az nagyobb vagy kisebb, mint a szimulációban résztvevő elektronok száma az alsó vagy felső energiaértékét felülírja és újra veszi a számtani közepüket. Ezt addig folytatja, ameddig az éppen aktuális energiaszintig kiszámított betöltött állapotok száma meg nem egyezik a számolásban résztvevő elektronok számával. A pontossági kritérium szerint a kétféle töltés különbsége nem lehet nagyobb, mint \( 10^{-10} \). Ha a kritérium teljesül, akkor azt az energiát jelöli ki, mint Fermi-energia. Ebből az is következik, hogy tiltott sávval rendelkező anyagok esetén a SIESTA a Fermi-energiát a tiltott sávon belül teljesen véletlenszerűen helyezi le. Az általunk vizsgált tulajdonságok szempontjából csak az volt fontos, hogy a tiltott sávval rendelkező anyagok esetén a Fermi-energia valóban a tiltott sávban legyen, a pontos helyzete számunkra nem volt releváns a szigetelők esetén sem.
Válaszok a bírálói kérdésekre
Széchenyi Gábor kérdései.
2. A 4.2 táblázatban a Jelölt különböző halogén tartalmú BiTeX-grafén és BiTeX-grafén BiTeX rendszerek alacsony energiás tartományára illesztett modell paramétereit foglalja táblázatba különböző halogenidek esetén. Meglepő, hogy a legtöbb paraméter szendvics szerkezeteknél független a halogén választástól, ellenben az egyoldalas esetekben erős függés látható (Pl.: mIII). Lehet-e erre fizikai magyarázatot találni? Vagy a nagy eltérések az illesztés pontatlanságából jönnek?
Az illesztés során elsőként a sávszerkezet információkat vetettem össze a szoros kötésű modell diszperziós relációjával a különböző paraméterkiosztások esetén. Ezután megvizsgáltam, hogy a topologikus tulajdonság és a spin struktúra is visszaadja-e a SIESTA eredményeit. Azokat a paraméterkiosztásokat, amelyek az összes feltételt teljesítették, kigyűjtöttem. Minden illesztés esetén több száz ilyen paraméter készlet halmozódott fel. A legvégén a dolgozatba azt az egyet választottam ki, amelyik a legjobb egyezést mutatta. A maradék, továbbra is relatíve jól illeszkedő paraméterkiosztásból nem olvasható ki meggyőző összefüggés a paraméterek között. Kivételt képez ez alól kettő: a Kane-Mele típusú másodszomszéd spin-pálya kölcsönhatás nagysága és a Kekulé-torzítás erőssége. Ez a kettő egyértelműen reagált a nyomásra, azonban az összes többi paraméter úgy tűnt csak azért felel, hogy az egyezés a lehető legjobb legyen. Ezért úgy gondolom, hogy ilyen jól kézzelfogható magyarázatot a konkrét számértékekre nem lehet találni. Ha nem is az illesztés pontatlanságából, de inkább a túl nagy paramétertérből adódik az egyszerűség hiánya.
Válaszok a bírálói kérdésekre
Széchenyi Gábor kérdései.
3. A 67. oldalon olvasható: „Elsőként az egytengelyű nyújtást nem tartalmazó minden nyo-más értéknél megillesztettem a sávszerkezetet a modellhez.” Hogyan függenek az illesz-tett modell paraméterei a nyomás értékektől? Található-e olyan egyszerű fizikai modell, mellyel ezen paraméterek nyomásfüggése megérthető? Ez segíthetne, hogy a nyomás-függést be lehessen építeni az egyszerű szoroskötésű közelítésen alapuló modellbe.
Az illesztések során nagy erőfeszítést tettünk azért, hogy találjunk egy jól megfogható, egyszerű összefüggést a paraméterek értéke és a nyomás nagysága között. Sajnos, ahogyan már az előző kérdésnél kifejtettem ebben a kérdésben nem jártunk sikerrel.
Válaszok a bírálói kérdésekre
Széchenyi Gábor kérdései.
4. A Jelölt a topologikus invariánst csempe módszerrel is meghatározta. A második fejezetben hexagonális bór-nitrid és bizmutén esetében demonstrálta a módszer érvé-nyességét, melyhez a fél BZ-t 10*20-as rácsra osztotta fel. Milyen felosztást használt a Jelölt a BiTeX alapú rendszerek számolása során? Mi határozza meg, hogy milyen sűrű felbontásra van szükség a csempemódszernél?
A csempemódszerben alkalmazott rács felbontása függ a tiltott sáv nagyságától. Ha a tiltott sáv nagy, akkor kevesebb felosztás is elegendő és fordítva, ha a tiltott sáv kicsi, akkor a felbon-tást növelni kell. Éppen ezért a csempemódszerben a felbontást is konvergáltatni kell.
Válaszok a bírálói kérdésekre
Széchenyi Gábor kérdései.
5. Mi a Jelölt véleménye, hogy a BiTeX családból, melyik halogént érdemes választani kísérletileg, hogy a grafént topologikus szigetelővé tegyük? Milyen más lehetőségek vannak a grafén topologikus szigetelővé tételére, és mi ezen módszerek előnye és hátránya a BiTeX-szel szendvicselt grafénhoz képest?
A három különböző családtagból a BiTeCl-t rögtön kizárnám, ugyanis a másféle periodicitása miatt úgy gondolom az exfóliálás és a grafénra helyezés is problémásabb lehet. A kilépési munkák alapján a BiTeI és a BiTeBr közül egyértelműen a BiTeBr kerül ki nyertesnek, a grafén és a BiTeBr kilépési munkája szinte azonos, ezért a BiTeBr / grafén rendszerek esetén a grafén Dirac-kúpjai várhatóan a BiTeBr tiltott sávjának közepébe esnének, így a közös rendszer Fermi-energiája távolabb lenne a zavaró BiTeBr sávoktól.
A grafén topologikus szigetelővé tételére az elméleti próbálkozás általában az általam is használt van der Waals heterostruktúra konstruálása, csak más anyagokkal (például Bi2Se3). Egy másik lehet-séges eljárás, hogy szennyező atomokat juttatunk a grafén felszínére kis koncentrációban (például indiumot vagy talliumot ). A szennyező atomok előnye, hogy segítségükkel akár hőmérséklettől függő topologikus fázisokat is elérhetünk. Hátránya, hogy nem megfelelő szennyező atom esetén mágnesség jelenhet meg, illetve a koncentrációt is nehéz kordában tartani.
Válaszok a bírálói kérdésekre
Pályi András kérdései.
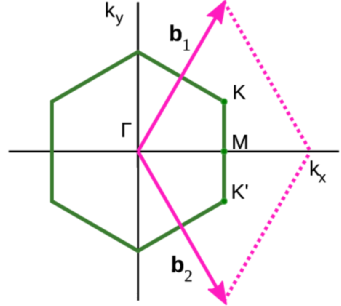
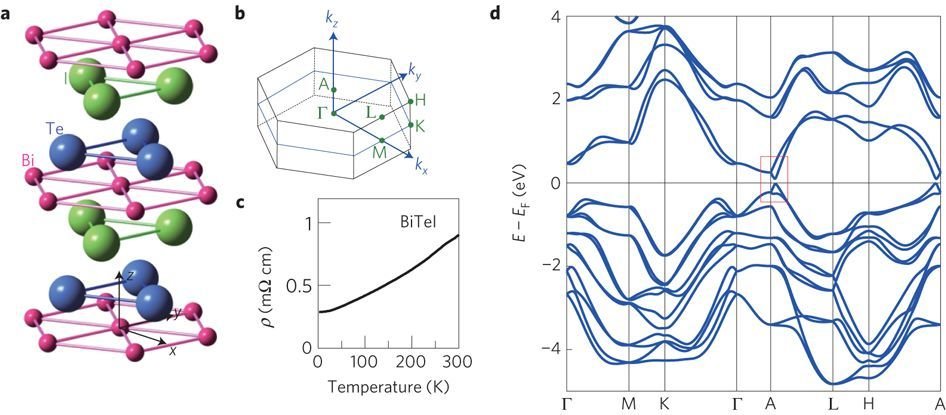
1. A 3.2 ábra 2D és 3D anyagok sávszerkezeteit mutatja be, hivatkozva a Brillouin-zóna nevezetes pontjaira. Érdemes lett volna ezen ábra előtt egy másik ábrán bemutatni ezen anyagok Brillouin-zónáit, és azon az ábrán definiálni a nevezetes pontokat.
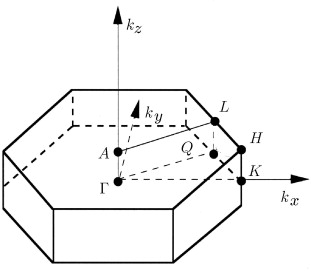
Szeretném megköszönni Pályi Andrásnak, hogy erre a hiányosságra felhívta a figyelmemet. Az alábbiaknak szeretném kijavítani a hibát és bemutatni a vizsgált rendszerek Brillouin-zónáit. A vizsgált háromdimenziós anyagok Brillouin-zónája hatszög alapú hasáb, míg a kétdimenziós változatuké egy a hatszög alapú hasáb alapja, így lehet beszélni a két zónáról összefoglalóan.
A grafénhoz hasonlóan a BiTeX egyrétegű rendszereknek is három magas szimmetriájú pontja van. A Brillouin-zóna közepe (a \( \Gamma \) pont), a hatszög csúcsai (\( K \) pont) és a hatszög oldalainak felezőpontjai (szokásosan pont, mely az ábrán -val van jelölve). A BiTeX háromdimenziós változatainak Brillouin-zónája úgy épül fel, hogy a hatszög alapját a síkra merőleges reciprokrácsvektor felezőpontjáig feltoljuk. Így kapjuk a következő három magas szimmetriájú pontot, sorrendben az , a és az pontot.
Válaszok a bírálói kérdésekre
Pályi András kérdései.
2. A 3.2 ábrán látható sávszerkezetek közül mindegyik triviális? Vagy van köztük topologikus szigetelő?
A dolgozatomnak további hiányossága, hogy a 3.2 ábrán látható sávszerkezetekben található tiltott sávok topologikus tulajdonságairól nem ejt szót. A munkánk során megvizsgáltuk mindhárom anyag tömbi és egyréteges szerkezetének topologikus invariánsát és mind a hat esetben azt találtuk, hogy a tiltott sávok triviálisak.
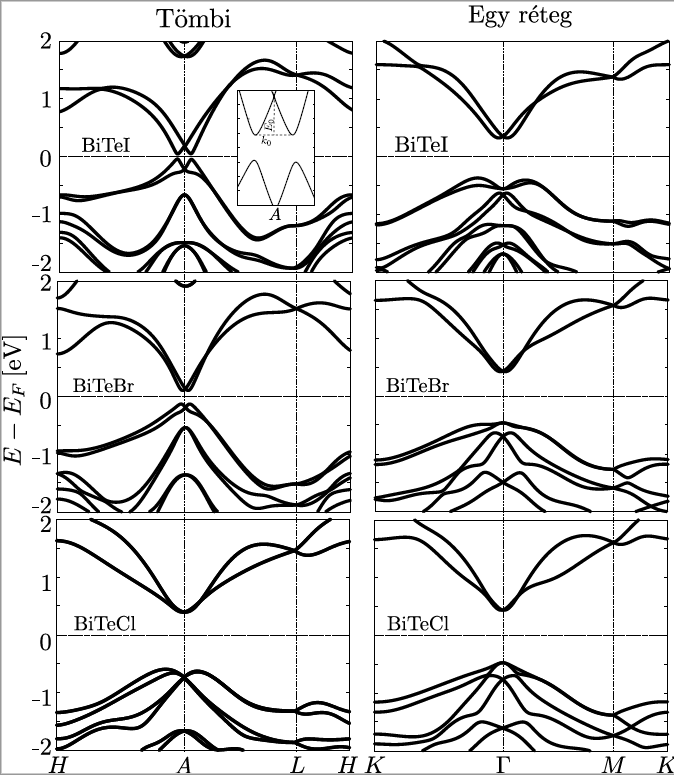
Válaszok a bírálói kérdésekre
Pályi András kérdései.
3. A jelölt által használt modellek alapfeltevése, hogy az egymással érintkező anyagi rétegek (pl. grafén és BiTeI) kommenzurábilis rácsszerkezetet alkotnak. Milyen viszonyban van ez a feltevés a valósággal? Kijöhetnek-e érdekes jelenségek, ha a feltételezett kommenzurabilitás nem teljesül?
Ha a kommenzurábilitás sérül, például valamilyen nem triviális szögben elforgatjuk egymáshoz képest a két rácsot, akkor a közeli tellúr atomok kikerülhetnek a szén hatszögek közepéből. Meg kell vizsgálni, hogy a tellúr atomok elhelyezkedése hogyan befolyásolja a modelljeinkben bevezetett paramétereket, főként a Kekulé torzítás és a Kane-Mele másodszomszéd spin-pálya kölcsönhatást. Ha továbbra is számíthatunk arra, hogy ezek az effektusok megjelennek, csak már rendezetlenül, akkor a Kekulé torzítás és a Kane-Mele kölcsönhatás egy másikfajta versengésbe kezdenek. Ahhoz, hogy a Kekulé-torzítás tiltott sávot tudjon nyitni egy bizonyos fajta rendeződésére van szükség, ellenben a Kane-Mele-féle kölcsönhatásnak nincs ilyen irányú követelménye. Ezért azt várom, hogy nem kommenzurábilis elrendeződések esetén is a topologikus tiltott sáv fog érvényesülni.
Válaszok a bírálói kérdésekre
Pályi András kérdései.
4. A 4.4 ábrán az egytengelyű megnyújtást a 0 és 1% közti ablakban vizsgálja a jelölt. Milyen módszerrel, és milyen mértékű nyújtást lehet elérni kísérletileg ezekben az anyagokban?
Többek között azért is vizsgáltuk a mutatott ablakot, mert kísérleti szempontból az egytengelyű nyújtás határa grafénban, ami még rutinszerűen megvalósítható, valahol éppen az 1% környékén van. Zhen Hua Ni és munkatársai publikációjukban[1] Raman-spektrumot mértek miközben három rétegű grafitot, illetve grafént nyújtottak egytengelyű nyújtással. Mindkét esetben egészen 1%-nak megfelelő mechanikai feszültséget tudtak kelteni az anyagokban.
[1] Zhen Hua et. al. ACS Nano 2009, 3, 2, 483
Válaszok a bírálói kérdésekre
Pályi András kérdései.
5. A 4.5 ábrán látható numerikus fázisdiagramok milyen x-y felbontással készültek? Nekem úgy tűnik, mintha az ábrakészítő szoftver automatikus interpolációt végzett volna, emiatt a használt felbontás nem érzékelhető, illetve az ábra nem a tényleges eredményeket tükrözi. Jól látom ezt? Ha igen, akkor javaslom, hogy készítsen ugyanezen adatokból egy ugyanilyen ábrát, csak interpoláció nélkül.
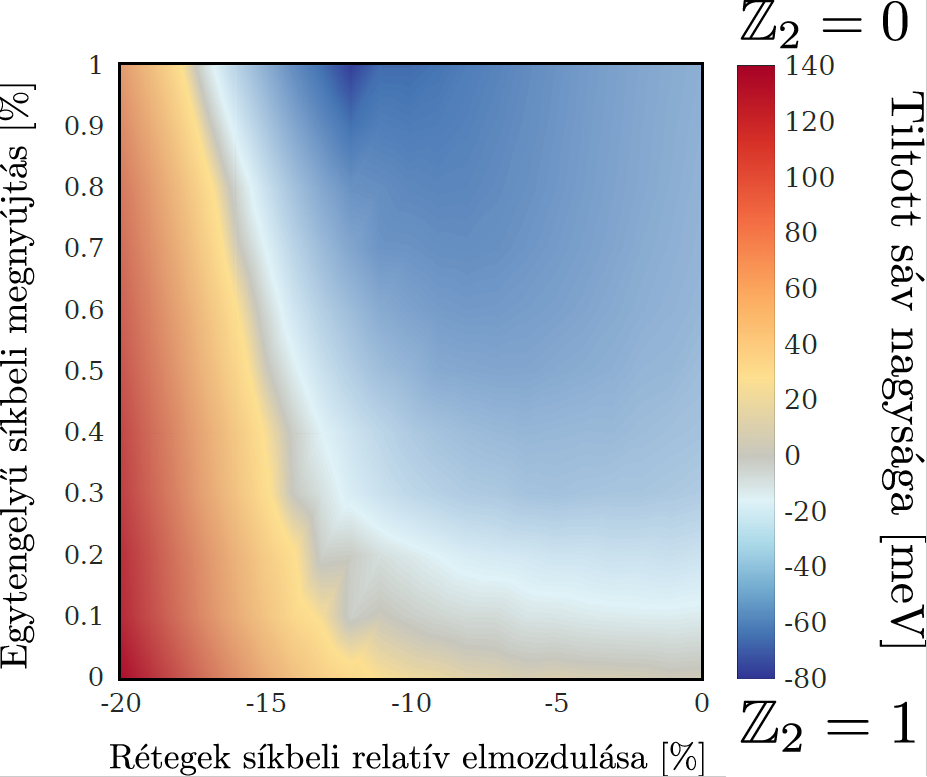
Válaszok a bírálói kérdésekre
Pályi András kérdései.
6. Validálta-e a tömbi adatokból számolt Z2 invariáns értékeket nanoszalagok élállapotainak vizsgálatával?
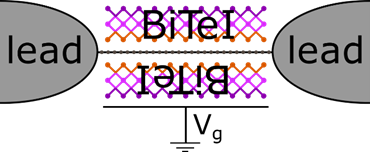
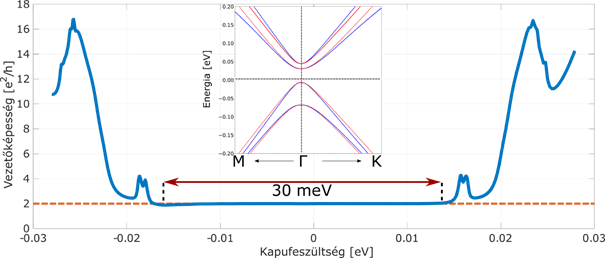
Egy korábbi munkánk során, ami az MSc-s diplomamunkám nagy része volt, a szendvics szerkezetre illesztett szoros kötésű modellt használtuk arra, hogy egy nanoszalagon transzport számításokat végezzünk, melyekben látszódott a vezetőképesség kvantáltsága. Mivel a kétféle modell nagyon hasonlóan épül fel és a bennük szereplő paraméterek szerepe is hasonló, így azt várom, hogy ezek a modellek is reprodukálják az élállapotokat egy nanoszalag vizsgálata esetén.
Válaszok a bírálói kérdésekre
Pályi András kérdései.
6. Validálta-e a tömbi adatokból számolt Z2 invariáns értékeket nanoszalagok élállapotainak vizsgálatával?
Az 4. ábrán látható elrendezésben vizsgáltuk a szendvics szerkezet elektromos tulajdonságát egy sűrűségfunkcionál elmélet eredményeihez illesztett szoros kötésű modellben az EQuUs szoftvercsomag segítségével, miközben egy képzeletbeli kapufeszültség hatását szimuláltuk azáltal, hogy változtattuk a rendszerben az onsite potenciált. Azt találtuk, hogy amikor a kapufeszültség értéke a tiltott sávban volt, akkor a rendszer vezetőképessége nem nullára megy le, hanem platót mutat, a 5. ábrának megfelelőlen. Ez a viselkedés a védett élállapotok jele.
Válaszok a bírálói kérdésekre
Pályi András kérdései.
6. Az eredmények alapján a BiTeBr-grafén és BiTeCl-grafén heteroszerkezetek akár több tíz millielektronvoltos tiltott sávval rendelkező topologikus szigetelők is lehetnek, ha megfelelően deformálják őket. Tudna vázolni egy konkrét kísérleti elrendezést, amiben ez a topologikus szigetelő viselkedés tettenérhető lenne? (Milyen hőmérsékletre van szükség? Hogyan lehet létrehozni a szükséges deformációt? Mit kellene mérni?)
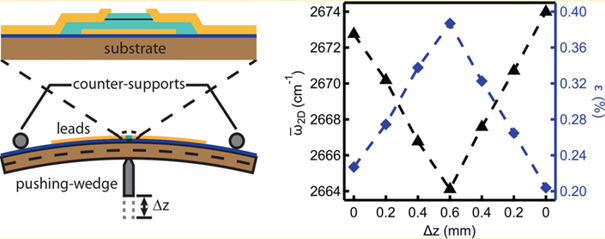
[1] Lujun Wang, et. al. Nano Lett. 2019, 19, 6, 4097–4102
Válaszok a bírálói kérdésekre
Pályi András kérdései.
6. Az eredmények alapján a BiTeBr-grafén és BiTeCl-grafén heteroszerkezetek akár több tíz millielektronvoltos tiltott sávval rendelkező topologikus szigetelők is lehetnek, ha megfelelően deformálják őket. Tudna vázolni egy konkrét kísérleti elrendezést, amiben ez a topologikus szigetelő viselkedés tettenérhető lenne? (Milyen hőmérsékletre van szükség? Hogyan lehet létrehozni a szükséges deformációt? Mit kellene mérni?)
[1] Lujun Wang, et. al. Nano Lett. 2019, 19, 6, 4097–4102
Válaszok a bírálói kérdésekre
Pályi András kérdései.
6. Az eredmények alapján a BiTeBr-grafén és BiTeCl-grafén heteroszerkezetek akár több tíz millielektronvoltos tiltott sávval rendelkező topologikus szigetelők is lehetnek, ha megfelelően deformálják őket. Tudna vázolni egy konkrét kísérleti elrendezést, amiben ez a topologikus szigetelő viselkedés tettenérhető lenne? (Milyen hőmérsékletre van szükség? Hogyan lehet létrehozni a szükséges deformációt? Mit kellene mérni?)
A kísérlet során számos aspektust lehetne vizsgálni.
- Milyen hőmérsékletre van szükség? A számolásaink során a 0,4%-os megnyúlás esetén a topologikus tiltott sáv nagysága eléri a 25 meV-t, sőt meg is haladja azt. A kísérlet szempontjából mindenképpen érdekes kérdés lenne, hogyan viselkedik az állapot a hőmérséklet függvényében, de a tiltott sáv nagysága alapján ekkora meghúzás esetén már szobahőmérsékleten is látható a jelenség. 0,2%-os megnyújtás esetén a tiltott sáv nagysága 12 meV, ami bőven a folyékony nitrogén hőmérséklete felett van, amivel a mintát hűteni lehetne.
- Milyen széles mintát kell gyártani? A minta húzás irányára merőleges szélessége azért érdekes kérdés, mert ha túlságosan keskeny a minta, akkor az élállapotok hullámfüggvényei átfedhetnek, minek következtében az élállapotok nem lesznek védettek. Mivel mind a grafén, mind a BiTeI esetén képesek voltak mikrométer nagyságrendben mintákat létrehozni korábban, így, ezek a heteroszerkezetek is várhatóan előállíthatók.
Védés 2021
By novidad21
