Open Momentum Space Method for Hofstadter Butterfly and the Quantized Lorentz Susceptibility
Journal Club
2021.03.01.
Zoltán Tajkov
https://arxiv.org/abs/2102.04479
Brief Introduction
- Calculating Hofstadter butterfly is hard in general
- It requires constructing complicated matrix elements
- Can we do it better?
- Spectral flows in spectrum
- Collateral gain: Chern number(s)
Continuum Models
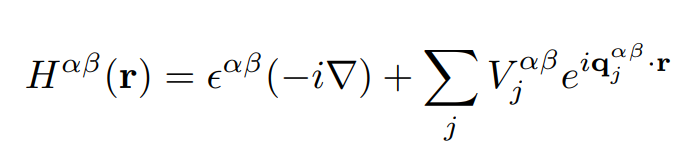
Kinetic term
Orbital indices
Lattice potential between orbitals
Momentum difference between sites
No magnetic field!
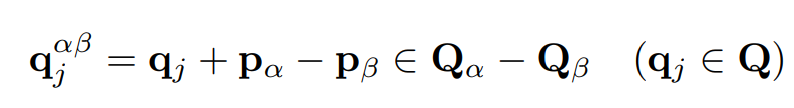
Reciprocal lattice space
Continuum Models
No magnetic field!
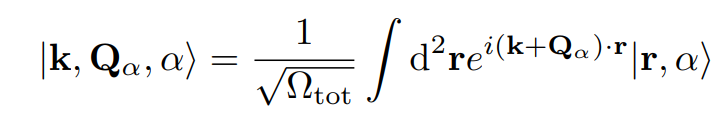
FT definition:
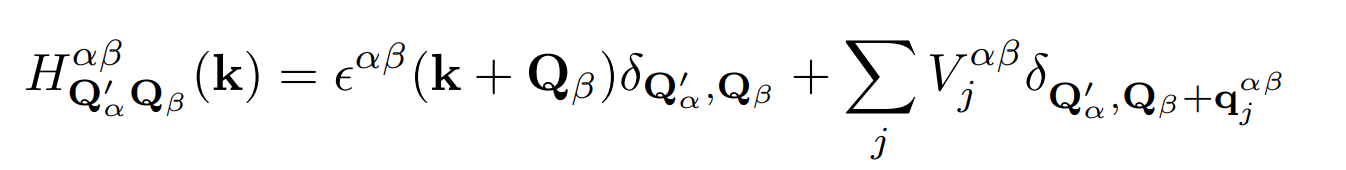
Continuum Models
Nonzero magnetic field!
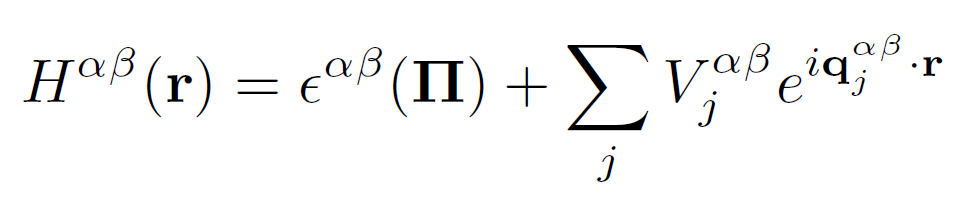
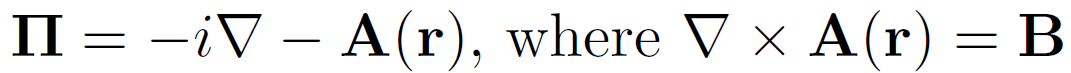
New basis! Make it block diagonal!
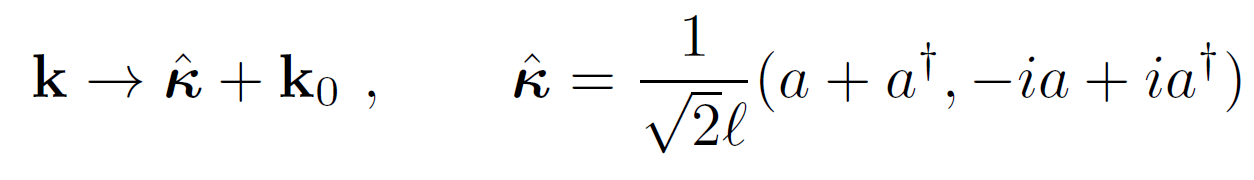
arbitrary momentum vector
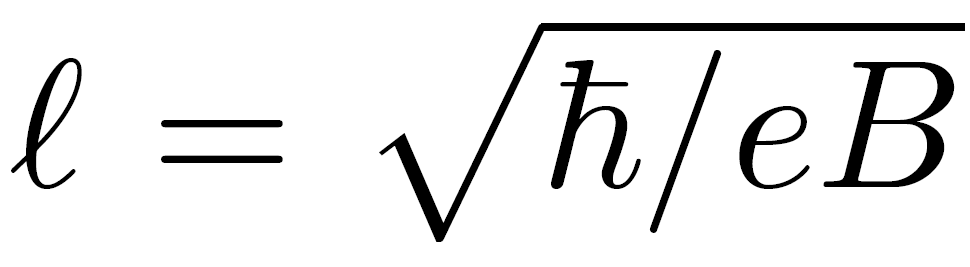
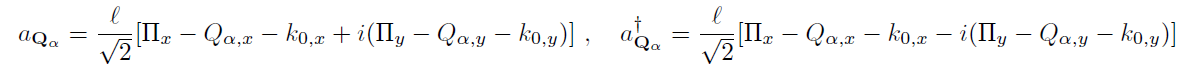
Continuum Models
Nonzero magnetic field!
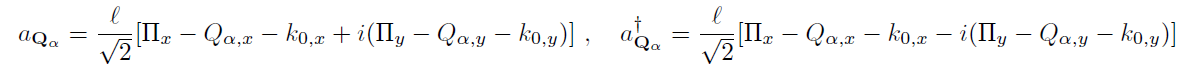
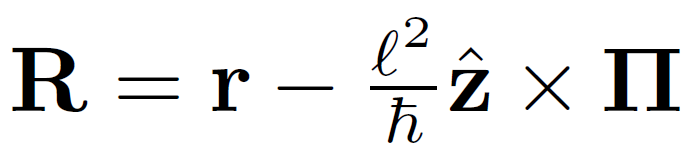
Secondly, guiding center:
It commutes with \( \mathbf{\Pi} \)
But use this instead:
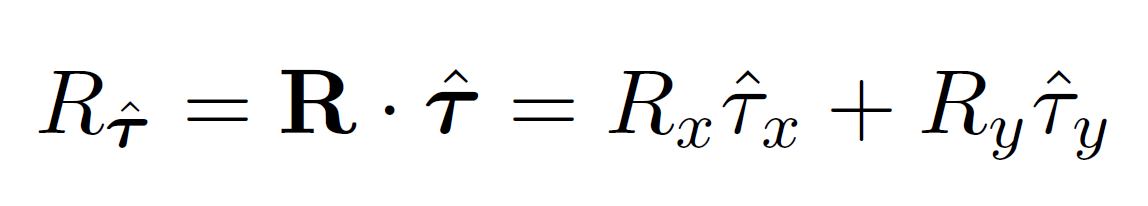
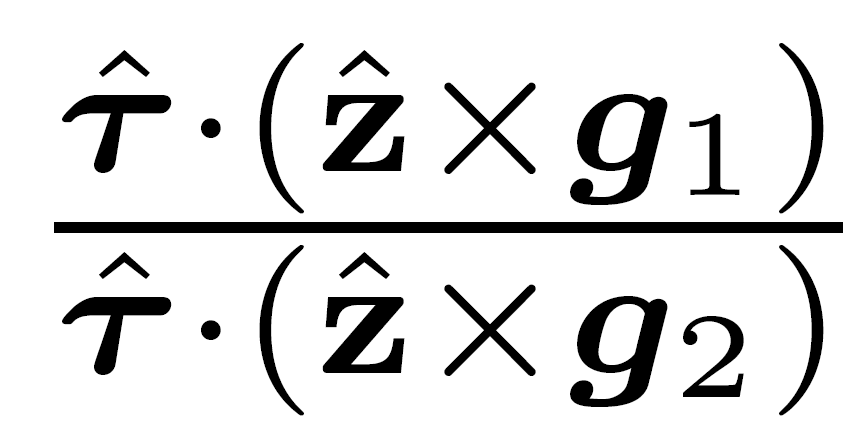
irrational
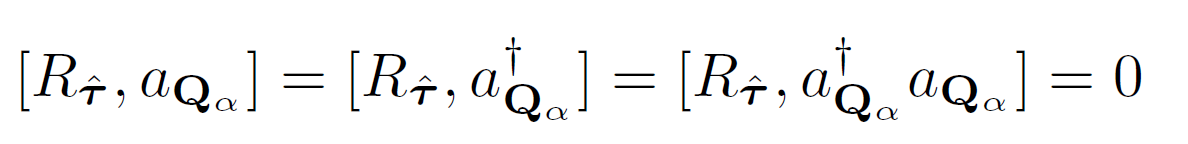
Not that clear why... :(
Continuum Models
New basis:
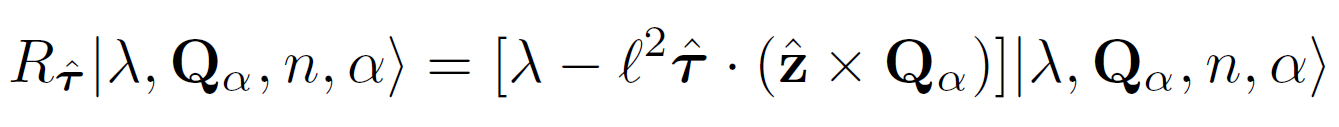
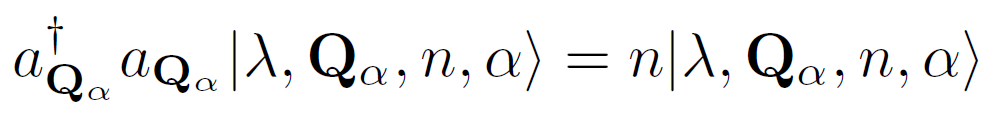
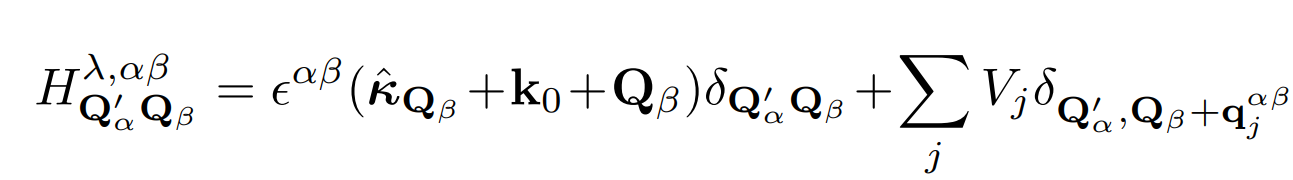
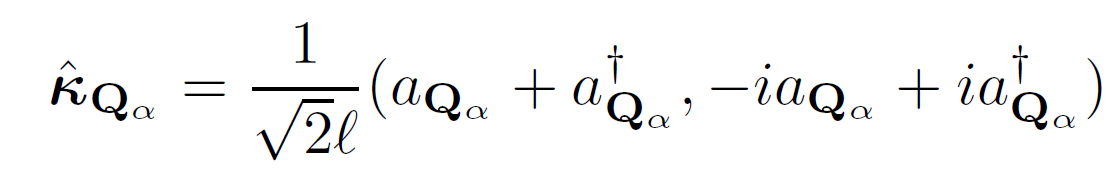
Continuum Models
New basis:
Advantages:
\( \mathrm{e}^{i\mathbf{q}_j^{\alpha, \beta}\cdot \mathrm{r}} \) operator doesn't change \( \lambda \)
For fixed \( \lambda \) the basis is orthonormal
\( V^{\alpha, \beta}_j \mathrm{e}^{i\mathbf{q}_j^{\alpha, \beta}\cdot \mathrm{r}} \) is diagonal in quantum numbers \( \lambda \) and \( n \) when acting on the basis, while changes the orbital from \( \beta \) to \( \alpha \), and shifts the reciprocal momentum \(\mathbf{Q}_\beta \) to \(\mathbf{Q}_\beta + \mathbf{q}_j^{\alpha, \beta} \).
Continuum Models
Numerical calculation
Two things are infinite:
- Reciprocal lattice space \( \rightarrow N_Q \)
- Landau levels quantum number \( \rightarrow n < N_L \)
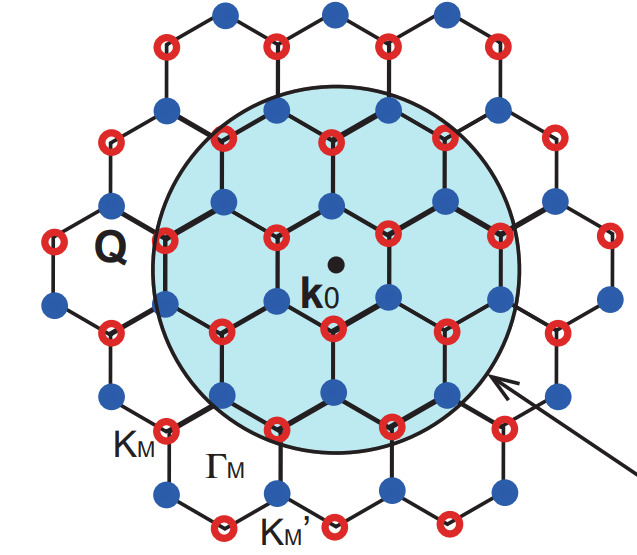
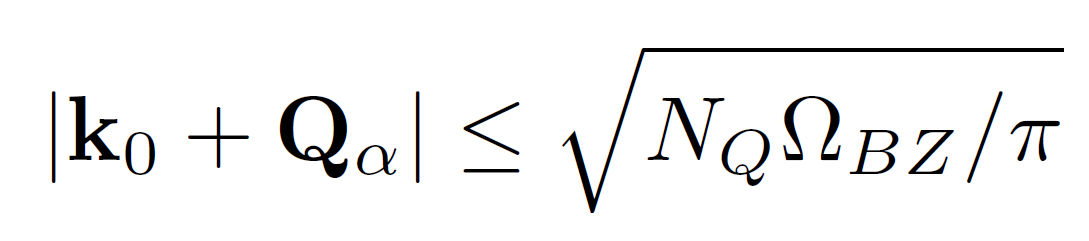
In addition:
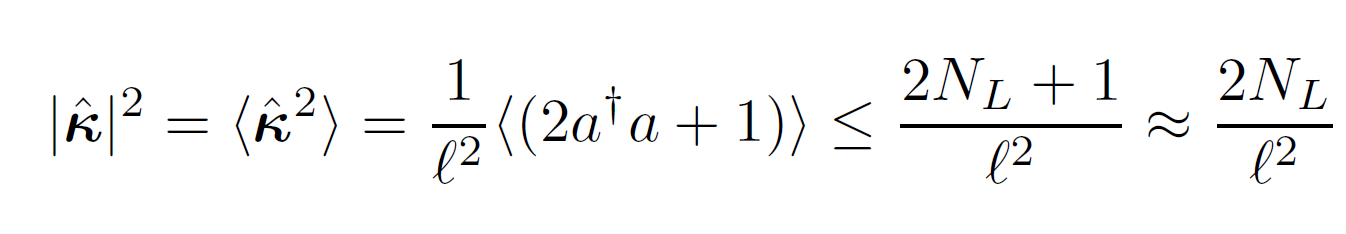
Continuum Models
Numerical calculation
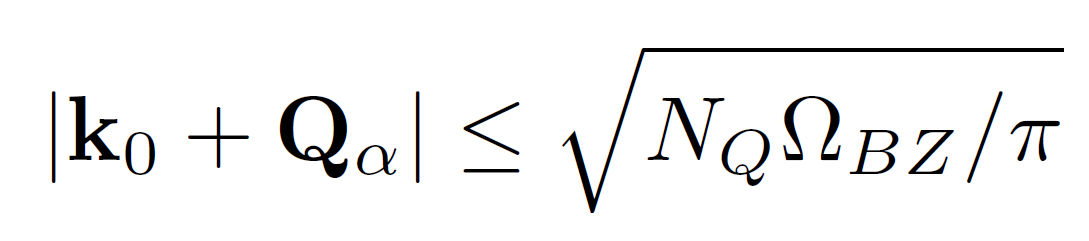
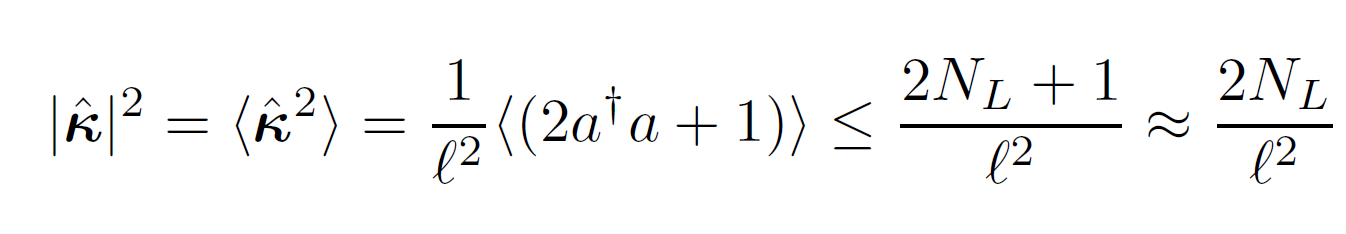
The two radius are equal, when:
\frac{\varphi}{2\pi}=\frac{N_Q}{N_L}
Therefore, we have two regions:
- \( \frac{\varphi}{2\pi} < \frac{N_Q}{N_L} \), \( \kappa \) has a hard cutoff \( \rightarrow \) momentum space boundary
- \( \frac{\varphi}{2\pi} > \frac{N_Q}{N_L} \) "cannot be a reliable eigenstate of the low energy Hofstadter bulk bands"
Continuum Models
Numerical calculation
Momentum boundary radius:
\kappa_b = \mathrm{min}\left ( \frac{\sqrt{2N_L}}{l}, \, \sqrt{\frac{N_Q \Omega_{BZ}}{\pi}} \right)
Any state with expectation value \( | \mathbf{\kappa}| > \kappa_b \) are effectively localized on the momentum space boundary at radius \( \kappa_b \) which we will call the momentum space edge states.
Continuum Models
Numerical calculation
Integers from spectral flows
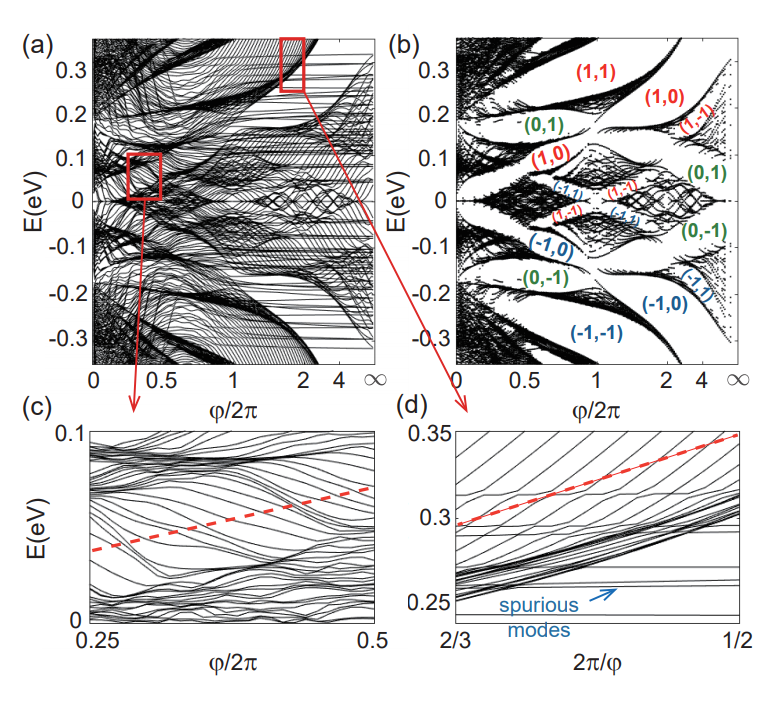
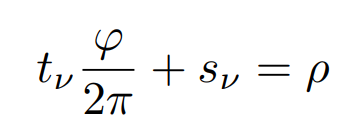
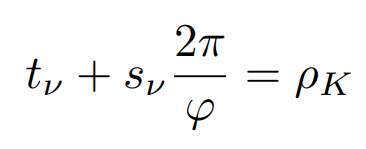
number of occupied bulk states per unit cell in the gap
\rho_K = 2\pi \rho / \varphi
(t_\nu,s_\nu)
Continuum Models
Numerical calculation
Integers from spectral flows
(t_\nu,s_\nu)
- \( t_\nu \) is the Chern number
- \( s_\nu \) is the "Lorentz susceptibility"
Continuum Models
Numerical calculation
Integers from spectral flows
(t_\nu,s_\nu)
- \( t_\nu \) is the Chern number
- \( s_\nu \) is the "Lorentz susceptibility"
\( t_\nu \rightarrow \) Hall conductivity, it gives a \( j_x = \partial H / \partial_{k_x} \) response to an external electric field
\( s_\nu \) duality \( \rightarrow \) \( F_x = \partial H / \partial_{x} \) response to a velocity
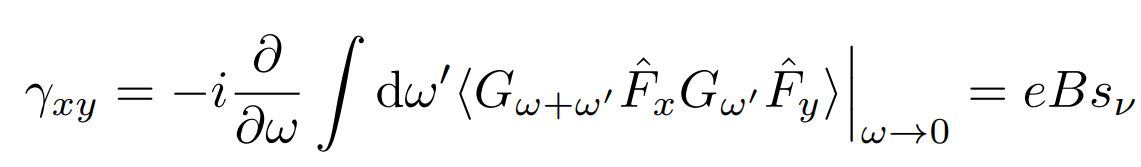
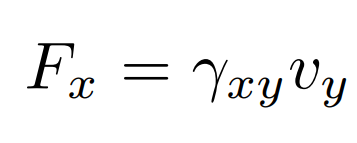
Journal Club 2
By novidad21
