Revealing the topological phase diagram of ZrTe5 using the complex strain fields of microbubbles
Centre for Energy Research, Institute of Technical Physics and Materials Science
Zoltán Tajkov


outline


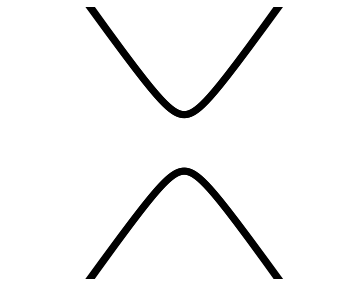
$$ E $$
$$ E $$

Insulator?
Topology?

$$ \frac{1}{2\pi}\int K \mathrm{d}A = 2(1-g) $$
$$ \frac{1}{2\pi}\int K \mathrm{d}A = 2(1-g) $$

Su-Schrieffer-Heeger
FT
J. K. Asbóth, et. al., vol. 909 of Lecture Notes in Physics. Springer International Publishing, 1st ed., 2016.
$$ \frac{1}{2\pi}\int K \mathrm{d}A = 2(1-g) $$

Su-Schrieffer-Heeger
vinding number
J. K. Asbóth, et. al., vol. 909 of Lecture Notes in Physics. Springer International Publishing, 1st ed., 2016.
What are topologic insulators good for?
- They are robust
- Their properties are not localised
- They depend only on fundamental constants
- Quantum computing
- Measurement of fundamental constants
- Spintronics
- Topologically protected edge states
Topological insulators are rare!


25%
Zirconium pentatelluride - ZrTe5
Mutch, J., Chen, et. al. Science Advances, 2019 5(8).
Zirconium pentatelluride - ZrTe5

Mutch, J., Chen, et. al. Science Advances, 2019 5(8).
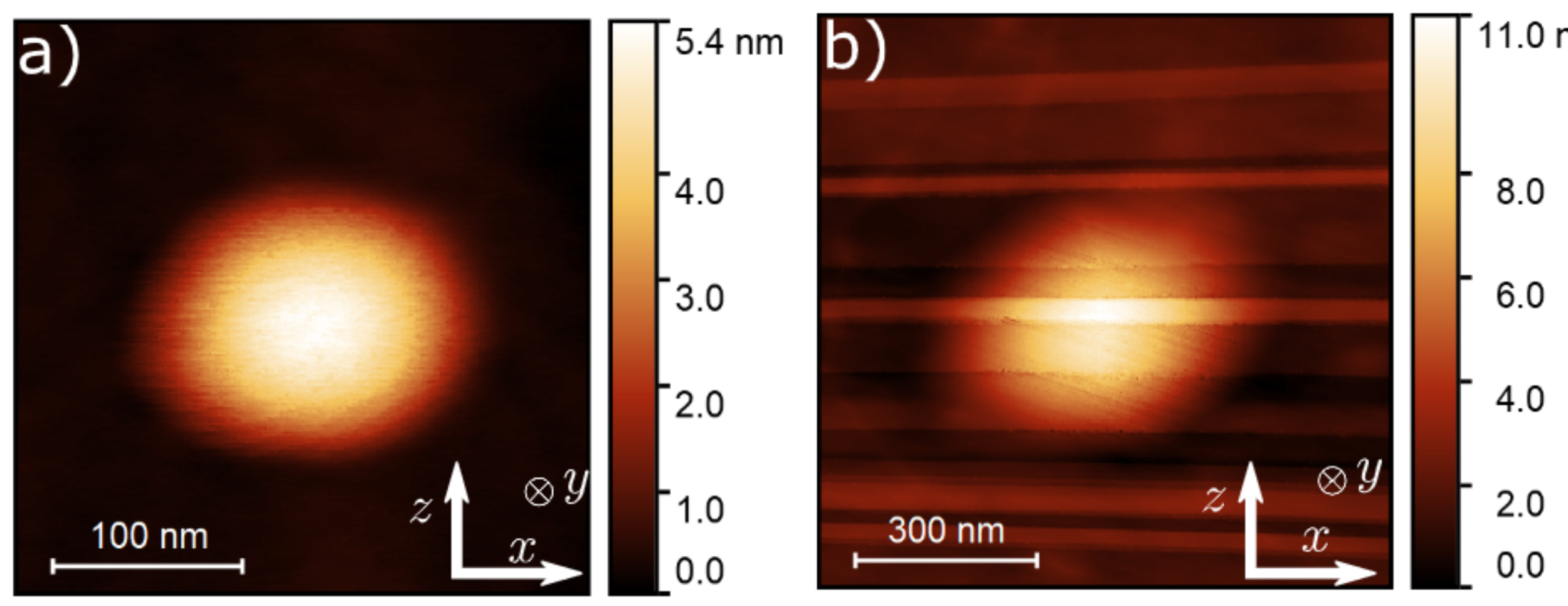
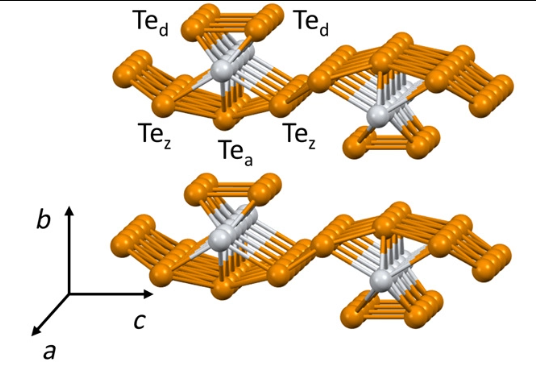
Zirconium pentatelluride - ZrTe5
$$ \#1 $$
$$ \#2 $$
$$ d $$
$$ h$$
$$ R_1 $$
$$ R_2 $$
$$ Ang $$
55
49
1015
813
178
90
6000
4560

Zirconium pentatelluride - ZrTe5

$$ O_x $$
$$ \mathcal{A}_1 $$
$$ \mathcal{B}_1 $$
$$ C $$
$$ O_z$$

$$ O_x $$
$$ \mathcal{A}_1 $$
$$ \mathcal{B}_1 $$
$$ C $$
$$ O_z$$
Stiffness tensor (DFT)
Finite Element Method
Electric properties (DFT)

Zirconium pentatelluride - ZrTe5
COMSOL and DFT

Zirconium pentatelluride - ZrTe5
Ab initio

Zirconium pentatelluride - ZrTe5
Ab initio

The team

János Koltai

Péter Nemes-Incze

Levente Tapasztó
Oroszlányi László


Péter Vancsó

Dániel Nagy
Talk in Regensburg 2022
By novidad21
Talk in Regensburg 2022
- 523



