Bifurcation of topological phases in two dimensional Ising superconductor NbSe2 Monolayer
Zoltán Tajkov
APCOM, June 21, 2024
Centre of Low Temperature Physics, Institute of Experimental Physics, Slovak Academy of Sciences
This work was supported by the Slovak Academy of Sciences project IMPULZ IM-2021-42
nbse2
F. Soto et al. / Physica C 460–462 (2007) 789–790
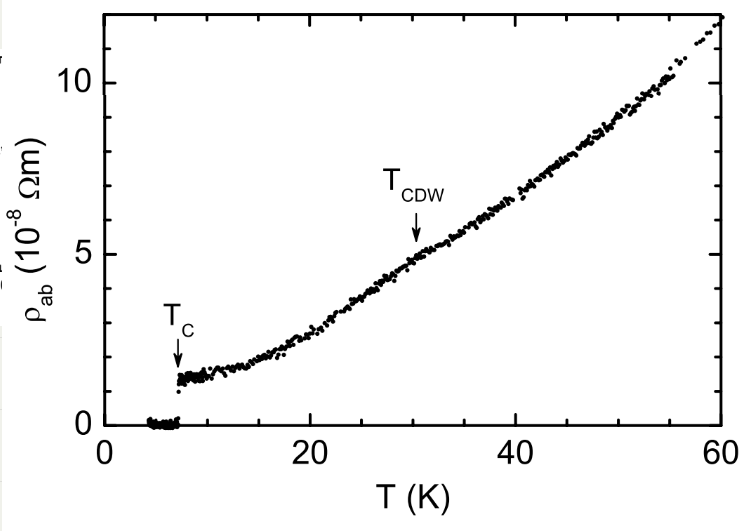
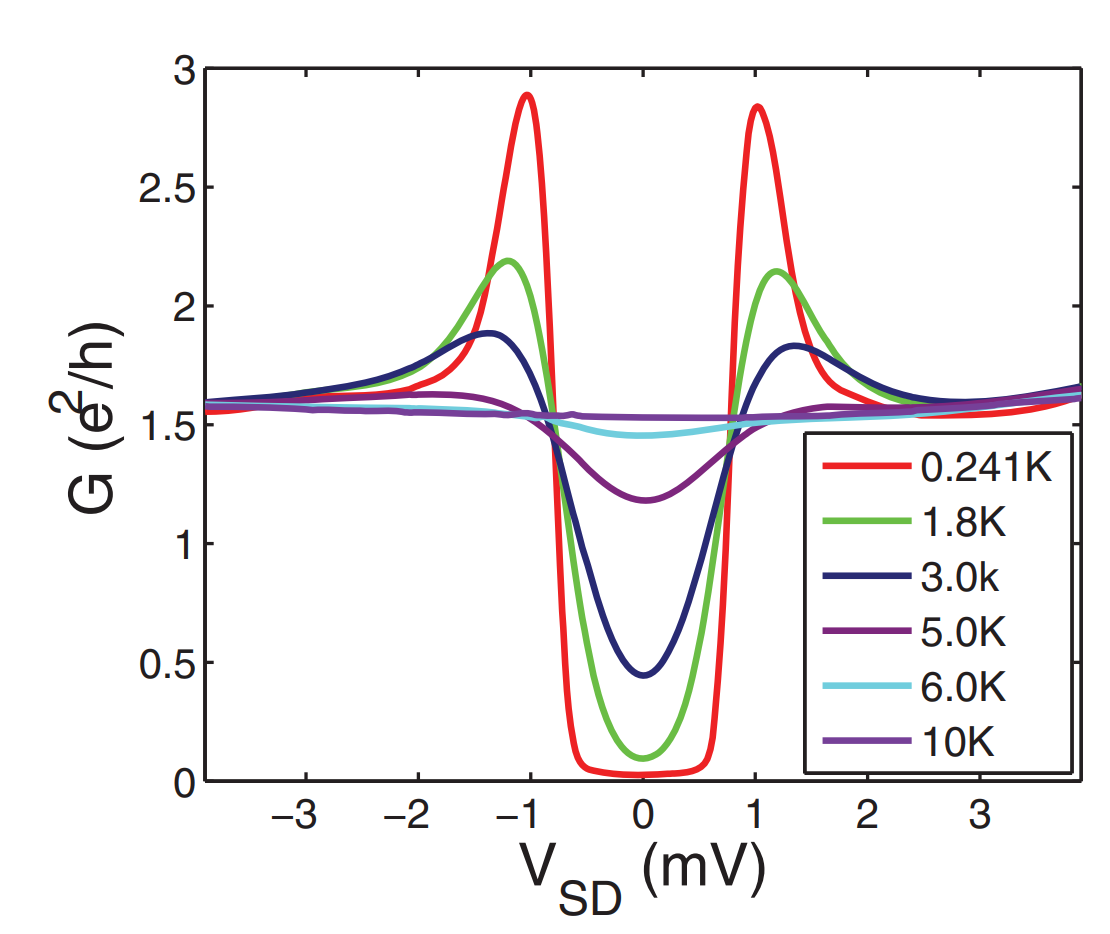
M. R. Sahu et al. Phys. Rev. B 94, 235451 2016
\( T_c \approx 7 K \)
\( 2\Delta \approx 2.7 \, \mathrm{meV} \)
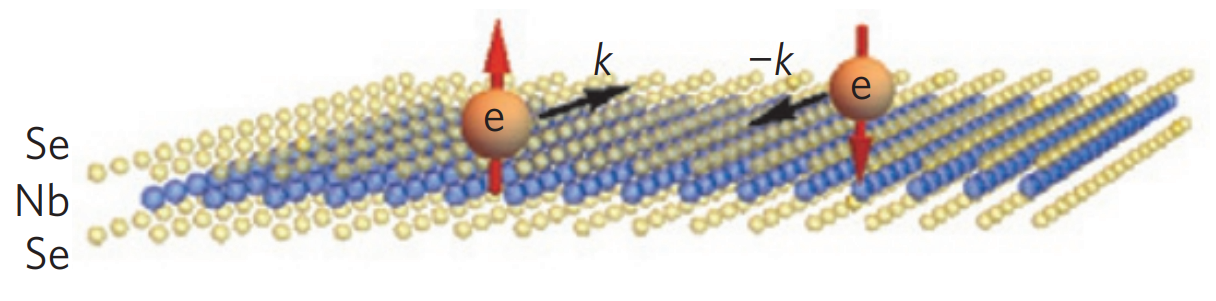
Xi, X., et al. Nature Phys 12, 139–143 (2016).
Ising superconductor
APCOM, June 21, 2024
nbse2
APCOM, June 21, 2024
Tight binding
description
- \( d \) characteristics
- Fitted to DFT up to 7 neighbors
- 1 electron / site + spin
Superconductivity from
Bogoliubov–de Gennes Hamiltonian
This gives us \( H_\mathrm{e}(\mathbf{k}) \rightarrow \)
\begin{equation*}
\mathcal{H}_{\mathbf{k}}^{\mathrm{BdG}} =
\begin{pmatrix}
H_\mathrm{e}(\mathbf{k}) & \Delta_{\mathbf{k}}\\
\Delta^{\dag}_{\mathbf{k}}& -H_\mathrm{e}^{\mathrm T}(-\mathbf{k})
\end{pmatrix}
\end{equation*}
\Delta_{\mathbf{k}}
nbse2
APCOM, June 21, 2024
\Delta_{\mathbf{k}}
What is
Special thank to
Marko Milivojević
General formulation
\begin{aligned}
\Delta_{A_1}^s(p,q) &= \sum_{g \in {\bf C}_{3v}} A^*_1(g) \cos{({\bf k} \cdot (g^{-1} {\bf r}_{p,q}))} d_0, \\
\Delta_{A_2}^s(p,q) &= \sum_{g \in {\bf C}_{3v}} A^*_2(g) \cos{({\bf k} \cdot (g^{-1} {\bf r}_{p,q}))} d_0, \\
\Delta_{E,1/2}^s(p,q) &= \sum_{g \in {\bf C}_{3v}} (E_{11/22}(g))^* \cos{({\bf k} \cdot (g^{-1} {\bf r}_{p,q}))} d_0.
\end{aligned}
\begin{array}{c|l}
A_1 & \Delta^{s}_{A_1}(1,0)=\left[2\cos{(k_x a)}+4\cos{\frac{k_x a}{2}}\cos{\frac{\sqrt{3}k_y a}{2}}\right]d_0 \\
& \Delta^{t,z}_{A_1}(1,0)=\left[\left(\cos{\frac{k_xa}{2}}-\cos{\frac{\sqrt{3}k_y a}{2}}\right)\sin{\frac{k_xa}{2}}d_z\right] \\
& \Delta^{t,xy}_{A_1}(1,1)=\left[ 3\cos{\frac{k_x a}{2}} \sin{\frac{\sqrt{3} k_ya}{2}}\right]d_x -\left[\sqrt{3}\left(2\cos{\frac{k_xa}{2}}+\cos{\frac{\sqrt{3}k_y a}{2}}\right)\sin{\frac{k_xa}{2}}\right]d_y \\ \hline
A_2 & \Delta^{s}_{A_2}(2,-1)=2 \left[\sin{\frac{k_xa}{2}}\sin{\frac{3\sqrt{3}k_ya}{2}}-\sin{(2k_xa)}\sin{(\sqrt{3}k_ya)}+\sin{\frac{5k_xa}{2}}\sin{\frac{\sqrt{3}k_ya}{2}}\right]d_0 \\
& \Delta^{t,z}_{A_2}(1,-1)=\left[\sin{(\sqrt{3}k_ya)}-2\sin{\frac{\sqrt{3}k_ya}{2}}\cos{\frac{3k_xa}{2}}\right]d_z \\
& \Delta^{t,xy}_{A_2}(1,0)=\left[\left(2\cos{\frac{k_xa}{2}}+\cos{\frac{\sqrt{3}k_y a}{2}}\right)\sin{\frac{k_xa}{2}}\right]d_x +\left[\sqrt{3}\cos{\frac{k_x a}{2}} \sin{\frac{\sqrt{3} k_ya}{2}}\right]d_y \\ \hline
E & \Delta_{E,{1/2}}^s(1,0)=\left[\cos{(k_xa)}-\cos{\frac{k_xa}{2}}\cos{\frac{\sqrt{3}k_ya}{2}}\pm{\rm i}\sqrt{3}\sin{\frac{k_xa}{2}}\sin{\frac{\sqrt{3}k_ya}{2}}\right] d_0 \\
& \Delta^{t,z}_{E,1/2}(1,0)=\left[\sin{(k_x a)}+\sin{\frac{k_xa}{2}}\cos{\frac{\sqrt{3}k_y a}{2}}\pm{\rm i}\sqrt{3}\cos{\frac{k_xa}{2}}\sin{\frac{\sqrt{3}k_ya}{2}}\right]d_z \\
& \begin{aligned}
\Delta^{t,xy}_{E,1/2}(1,2)=&\left[2\sin{(\sqrt{3}k_y a)}-\cos{\frac{3k_x a}{2}}\sin{\frac{\sqrt{3}k_ya}{2}}\pm{\rm i}\sqrt{3}\sin{\frac{3k_x a}{2}}\cos{\frac{\sqrt{3}k_y a}{2}}\right]d_x+\\
& \left[\sqrt{3}\sin{\frac{3k_xa}{2}}\cos{\frac{\sqrt{3}k_ya}{2}}\mp3{\rm i}\cos{\frac{3k_x a}{2}}\sin{\frac{\sqrt{3}k_y a}{2}}\right]d_y
\end{aligned}
\end{array}
nbse2
APCOM, June 21, 2024
\begin{aligned}
\Delta_{A_1}^s(p,q) &= \sum_{g \in {\bf C}_{3v}} A^*_1(g) \cos{({\bf k} \cdot (g^{-1} {\bf r}_{p,q}))} d_0, \\
\Delta_{A_2}^s(p,q) &= \sum_{g \in {\bf C}_{3v}} A^*_2(g) \cos{({\bf k} \cdot (g^{-1} {\bf r}_{p,q}))} d_0, \\
\Delta_{E,1/2}^s(p,q) &= \sum_{g \in {\bf C}_{3v}} (E_{11/22}(g))^* \cos{({\bf k} \cdot (g^{-1} {\bf r}_{p,q}))} d_0.
\end{aligned}
One more parameter
the chemical potential \( \mu \)
Now we have
- The representation: \( A_1, A_2, E_1, E_2 \)
- The strength of the pairing functions, 3 for each rep.
- The chemical potential
nbse2
APCOM, June 21, 2024
nbse2
APCOM, June 21, 2024
Is this even possible?
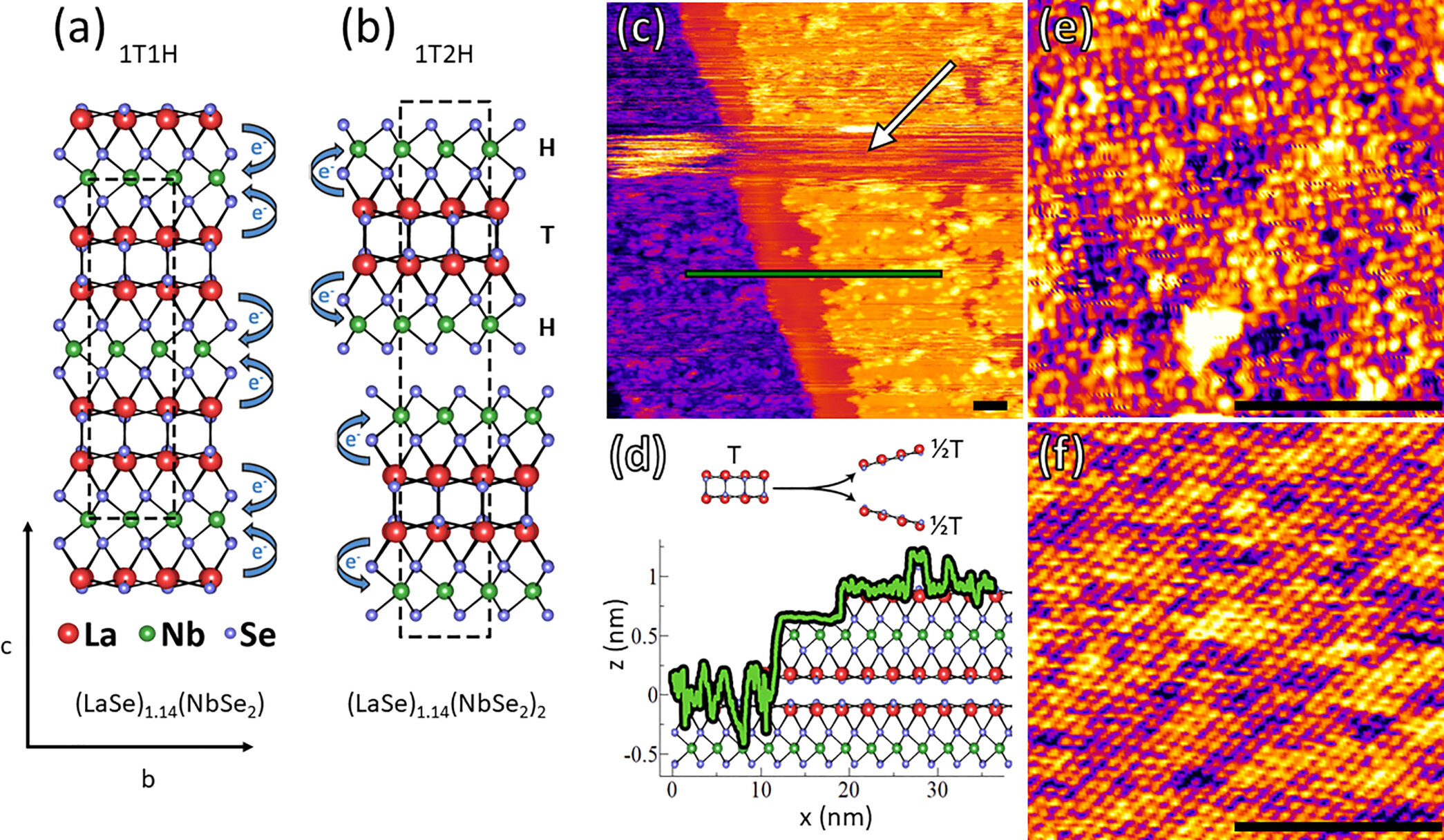
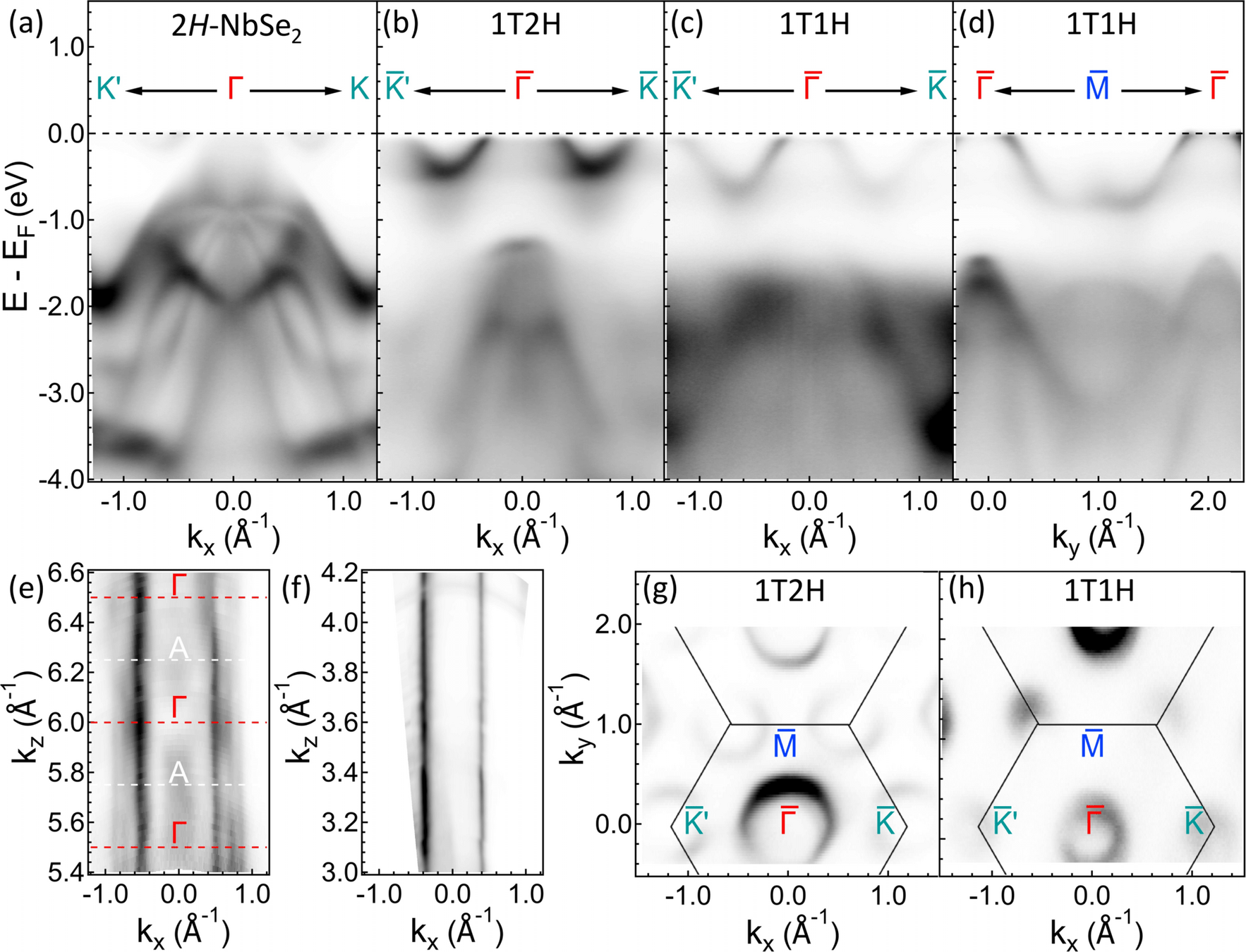
nbse2
APCOM, June 21, 2024
Is this even possible?
Talk in Tatras
By novidad21
