Introduction
2025-2026
Prof. Nele Vandersickel
Sander Hendrickx
biophysics.ugent.be
Why study dynamical systems?
Almost all systems are dynamical systems
Complex systems are everywhere! George Monbiot says the following:
All complex systems, including the global food system, possess emergent properties. This means that their components, however simple they each might be, behave in non-linear ways when they combine. [...]
Complex systems have thresholds. A system might be secure under some conditions, as its self-organising properties stabilise it. But when conditions change, and it is pushed towards a threshold, these self-organising properties have the opposite effect. Negative feedback loops are replaced by positive feedback loops, which compound the shocks afflicting the network, amplifying chaos. These thresholds can be hard to identify until they have been passed. They are often described as tipping points. Once a system has lost its resilience, a small disturbance can tip it over its critical threshold, at which point it collapses, suddenly and unstoppably.
You as a physicist have the privilege to understand complex systems, as many people do not grasp the ideas behind it.
I believe everyone should understand these systems as they are underlying so many urgent problems we face today.
Almost all systems are dynamical systems
But the earth's climate system is nowadays the most important one
Third revolution
-
First revolution: Newtonian mechanics (17th century) – Established the deterministic, law-governed view of nature. Motion of planets, falling apples, everything could be described with precise equations. This created the image of the universe as a “clockwork machine.”
Everything was predictable.
-
Second revolution: Relativity and Quantum Mechanics (early 20th century) – Overthrew the Newtonian worldview at both the very large (Einstein) and the very small (Planck, Schrödinger, Heisenberg). Physics shifted from absolute space and time to relativity, and from determinism to fundamental indeterminacy at the quantum scale.
Quantum mechanics said unpredictability comes from fundamental uncertainty.
-
Third revolution: Chaos theory and complexity (mid–late 20th century) – Discovered that even deterministic systems (like Newton’s equations) can behave in a way that looks random, due to extreme sensitivity to initial conditions. This shattered the simplistic “determinism = predictability” assumption of classical physics. Out of this grew nonlinear dynamics, fractals, and the broader field of complex systems.
Chaos theory showed that unpredictability also exists in classical, deterministic systems.
What is a Dynamical System?
- A rule that tells us how something evolves in time
-
Input: current state → Output: next state
-
Two kinds:
1. Continuous (differential equations)
2.Discrete (maps)

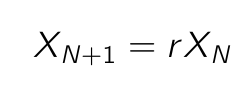
What is a Dynamical System?
Complex patterns can emerge from very simple rules
Examples
What do you need: Many interacting parts, nonlinear rules, collective behavior.
-
Physics:
-
Planetary motion
-
Turbulence
-
- Biology:
-
Population cycles, ecosystems
-
Ant colonies → emergent organization without a leader.
-
- Climate:
- Tipping points
- Ocean circulation.
-
Society:
-
Traffic jams,
-
Financial markets.
-
-
Medicine
-
Spread of disease,
-
Arrhythmia: waves of electrical signals that can become arrhythmias
-
The brain → neurons firing together create thoughts.
-
Complex systems are everywhere in science, not just physics.
Examples
Why study these systems
-
Predict: understand future behavior.
-
Classify: know which patterns are possible.
-
Control: prevent instabilities (engineering, medicine).
-
Transfer knowledge: insights in one field apply elsewhere.
By studying dynamical systems, we don’t just solve equations. We gain a universal language for prediction, classification, and control. That language is transferable across fields.
This course
Here in class
- Each week: theory (mostly on Monday, but can also sometimes be on Friday)
- Exercises on the computer, mostly on Friday
- Work students, other special reasons can follow class online: but not recommended in other situation! Tell me if you cannot follow class regularly!
- Feedback is key to growth in this class, please come regularly
-
Special class
Week 3: We will talk about writing code and how to create good figures
Week 4: You will get additional information on using widgets in Jupyter Notebooks
- Theory is based on the book: modeling of life (download on Ufora)
- Code/solutions will be shared on github
This course
Evaluation:
- Project one 5 points (around week 4)
- Project two 5 points (around week 9)
- Final project 10 points + oral presentation (normal exam)
- You work together in class for normal exercises, but make the projects individually
We grade
- Physics: you need to be correct
- Code: you need to be efficient
- Figures: as a scientist you need to be able to communicate
Questions
- We love them, challenge us, work with us, find better solutions, show us the scientist you want to become!
- Give us feedback, discuss with us, we are equals in this class
This course

Introduction
By Nele Vandersickel
Introduction
- 116



