Composition of
Arrows
and
Symmetric Monoidal Categories
in Scala
Oleg Nizhnik
Monads
trait Monad[F[_]] {
def pure[A](a: A): F[A]
def flatMap[A, B](a: A)(f: A => F[B]): F[B]
}Composition uses functions as continuations
- Have access to a wide language capabilities
- opaque
case study: Console
- Implement Console process. Should be able to
- read line
- write ine
- echo2 : read two lines from the input and print concatenated string to the output
- countGets calculate how many lines would be read
Attempt 1: Monads
sealed trait ConsoleM[X]
object ConsoleM {
case class Pure[A](x: A) extends ConsoleM[A]
case class Bind[A, B](x: ConsoleM[A], fab: A => ConsoleM[B]) extends ConsoleM[B]
case object GetLine extends ConsoleM[String]
case class PutLine(s: String) extends ConsoleM[Unit]
implicit val monad: Monad[ConsoleM] = new StackSafeMonad[ConsoleM] {
def pure[A](x: A): ConsoleM[A] = Pure(x)
def flatMap[A, B](fa: ConsoleM[A])(f: A => ConsoleM[B]): ConsoleM[B] = Bind(fa, f)
}
val getLine: ConsoleM[String] = GetLine
def putLine(s: String): ConsoleM[Unit] = PutLine(s)
} def echo2: ConsoleM[Unit] =
for {
x <- getLine
y <- getLine
_ <- putLine(x + y)
} yield x + y
def countGets[A](cm: ConsoleM[A]): Int = cm match {
case Pure(_) => 0
case GetLine => 1
case PutLine(_) => 0
case Bind(m, f) => countGets(m) + (??? : Int)
}Attempt 1: Monads
FAILED
Attempt 2: Applicatives
sealed trait ConsoleA[X]
object ConsoleA {
case class Pure[A](x: A) extends ConsoleA[A]
case class Ap[A, B](f: ConsoleA[A => B], x: ConsoleA[A]) extends ConsoleA[B]
case object GetLine extends ConsoleA[String]
case class PutLine(s: String) extends ConsoleA[Unit]
implicit val applicative: Applicative[ConsoleA] =
new Applicative[ConsoleA] {
def pure[A](x: A): ConsoleA[A] = Pure(x)
def ap[A, B](ff: ConsoleA[A => B])(fa: ConsoleA[A]): ConsoleA[B] = Ap(ff, fa)
}
val getLine: ConsoleA[String] = GetLine
def putLine(s: String): ConsoleA[Unit] = PutLine(s)
}Attempt 2: Applicatives
def countGets[X](ca: ConsoleA[X]): Int = ca match {
case Pure(_) => 0
case GetLine => 1
case PutLine(_) => 0
case Ap(f, x) => countGets(f) + countGets(x)
}
def echo2: ConsoleA[Unit] = {
val start = (getLine, getLine).tupled
putLine(???)
}FAILED
Arrows
trait Arr[->[_, _]] {
def lift[A, B](f: A => B): A -> B
def split[A, B, C, D](f: A -> B, g: C -> D): (A, C) -> (B, D)
def compose[A, B, C](f: B -> C, g: A -> B): A -> C
}Attempt 3: Arrows
sealed trait ConsoleArr[X, Y]
object ConsoleArr{
case class Lift[A, B](f: A => B) extends ConsoleArr[A, B]
case class AndThen[A, B, C](start: ConsoleArr[A, B], next: ConsoleArr[B, C])
extends ConsoleArr[A, C]
case class Split[A, B, C, D](first: ConsoleArr[A, B], second: ConsoleArr[C, D])
extends ConsoleArr[(A, C), (B, D)]
case object GetLine extends ConsoleArr[Unit, String]
case object PutLine extends ConsoleArr[String, Unit]
Attempt 3: Arrows
implicit val arrow: Arr[ConsoleArr] = new Arr[ConsoleArr] {
def lift[A, B](f: A => B): ConsoleArr[A, B] = Lift(f)
def split[A, B, C, D](
fab: ConsoleArr[A, B],
fcd: ConsoleArr[C, D]
): ConsoleArr[(A, C), (B, D)] =
Split(fab, fcd)
def compose[A, B, C](f: ConsoleArr[B, C], g: ConsoleArr[A, B]): ConsoleArr[A, C] =
AndThen(g, f)
}
val getLine: ConsoleArr[Unit, String] = GetLine
val putLine: ConsoleArr[String, Unit] = PutLine
def concat: ConsoleArr[(String, String), String] = Lift(tupled(_ + _)) def echo2: ConsoleArr[Unit, Unit] =
(getLine &&& getLine) >>> concat >>> putLine
val echo2Verbose: ConsoleArr[Unit, Unit] =
liftf((_: Unit) => ((), ())) andThen
(getLine split getLine) andThen concat andThen putLine
def countGets[X, Y](carr: ConsoleArr[X, Y]): Int = carr match {
case Lift(_) => 0
case AndThen(start, next) => countGets(start) + countGets(next)
case Split(first, second) => countGets(first) + countGets(second)
case GetLine => 1
case PutLine => 0
}Attempt 3: Arrows
SUCCESS
Arrow Use Cases
- Explicit sequential \ parallel computation
- Performance https://github.com/traneio/arrows
- Parsing
- Introspection
- Optimizations
- Strictness
Monoid
trait Monoid[A] {
def neutral: A
def combine(x: A, y: A): A
}
Category
trait Cat[->[_, _]] {
def id[A]: A -> A
def compose[A, B, C](f: B -> C, g: A -> B): A -> C
}
Isomorphism
case class <->[A, B](to: A -> B, from: B -> A) {
def section = compose(to, from) === id
def retraction = compose(from, to) === id
}
Monoidal category
Symmetric Monoidal Category
Tensor product is bifunctor
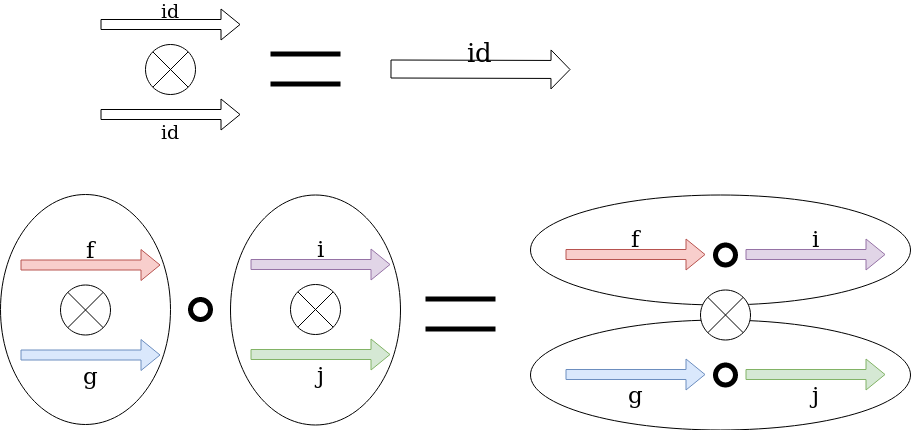
Pentagonal identity
Triagonal identity
Unit coherence
Associativity coherence
Coherence law
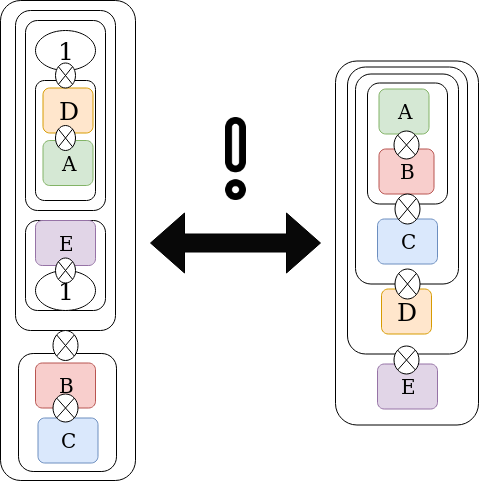
Symmetric Monoidal Category
trait Symon[->[_, _], x[_, _], I]{
def id[A]: A -> A
def compose[A, B, C](f: B -> C, g: A -> B): A -> C
def split[A, B, C, D](f: A -> B, g: C -> D): (A x C) -> (B x D)
def lunit[A]: (I x A) -> A
def unitl[A]: A -> (I x A)
def assocl[A, B, C]: (A x (B x C)) -> ((A x B) x C)
def swap[A, B]: (A x B) -> (B x A)
}
Symmetric Monoidal Category
Closed Monoidal Category
Cartesian Category
Cartesian Closed Category
Simply Typed Lambda Calculus
x : T \in \Gamma \frac{} {\Gamma \vdash x: T} Variable
\frac
{\Gamma \vdash f : A \to B ~~~~ \Gamma \vdash e: A}
{\Gamma \vdash f(e) : B}
Application
\frac
{\Gamma, x: A \vdash e: B}
{\Gamma \vdash (\lambda x: A. e) : A \to B}
Abstraction
\Gamma = \{ a : A, b : B, c : C \}
Curry-Howard
Correspondence
Logic
Type System
Category
-Lambek
Example
def name(id: UUID): String
def balance(id: UUID): BigDecimal
def plus(x: BigDecimal, y: BigDecimal): BigDecimal
def user(name: String, balance: BigDecimal): User
def total(main: UUID, secondary: UUID): User =
user(name(main), plus(balance(main), balance(secondary))) def name: UUID -> String
def balance: UUID -> BigDecimal
def plus: (BigDecimal x BigDecimal) -> BigDecimal
def user: (String x BigDecimal) -> User
def total: (UUID x UUID) -> User =
(product(name, balance) x balance) >>> assocr >>> (id[String] x plus) >>> user
Light Linear Lambda Calculus
\frac{} {x: T \vdash x: T} Variable
\frac
{\Gamma \vdash f : A \multimap B ~~~~ \Delta \vdash e: A}
{\Gamma, \Delta \vdash f(e) : B}
Application
\frac
{\Gamma, x: A \vdash e: B}
{\Gamma \vdash (\lambda x: A. e) : A \multimap B}
Abstraction
\Gamma = \{ a : A, b : B, c : C \}
\frac{} {\vdash (): 1} 1-intro
\frac{\Gamma \vdash e: A} {\Gamma, x : 1 \vdash e: A} 1-elim
Curry-Howard
Correspondence
Linear Logic
Linear Types
Monoidal Category
-Lambek
Volga
is comprehension syntax
for arrows
and symmetric monoidal categories
def echo2: ConsoleArr[Unit, Unit] =
(getLine &&& getLine) >>> concat >>> putLine
def echo2s: ConsoleArr[Unit, Unit] = arr { () =>
val s1 = getLine()
val s2 = getLine()
val s = concat(s1, s2)
putLine(s)
}Volga
trait Parsing[I, O] {
def parse(input: I): EitherNel[String, O]
def print(o: O): I
}Parsing
invertible parsing accumulating errors
def sep(sep: String): Parsing[String, (String, String)]
val readInt: Parsing[String, Int]
val date: Parsing[((Int, Int), Int), LocalDate]
import volga.syntax.comp._
import volga.syntax.cat._
import volga.syntax.symmon._
implicit val parsingSMC: Symon[Parsing, (*, *), Unit]
val parsing = symon[Parsing, (*, *), Unit]Parsing
val parseDate: Parsing[String, LocalDate] = parsing { (s: V[String]) =>
val (dayStr, monthYear) = sep(".")(s)
val (monthStr, yearStr) = sep(".")(monthYear)
----
val day = readInt(dayStr)
val month = readInt(monthStr)
val year = readInt(yearStr)
date(day, month, year)
}
Volga
val parseDate1: Parsing[String, LocalDate] = sep(".")
.andThen(ident[Parsing, String].split(sep(".")))
.andThen(parsingSMC.assocl[String, String, String])
.andThen(readInt.split(readInt).split(readInt))
.andThen(date)Volga
val parseDate1: Parsing[String, LocalDate] = parsing { (s: V[String]) =>
val (dayStr, monthYear) = sep(".")(s)
val (monthStr, yearStr) = sep(".")(monthYear)
----
val year = readInt(yearStr)
val month = readInt(monthStr)
val day = readInt(dayStr)
date(day, month, year)
}Volga
Change the order
val parseDate: Parsing[String, LocalDate] = sep(".")
.andThen(ident[Parsing, String].split(sep(".")))
.andThen(
parsingSMC
.assocl[String, String, String]
.andThen(parsingSMC.swap[String, String].split(ident[Parsing, String]))
.andThen(parsingSMC.assocr[String, String, String])
.andThen(ident[Parsing, String].split(parsingSMC.swap[String, String]))
.andThen(parsingSMC.assocl[String, String, String])
.andThen(parsingSMC.swap[String, String].split(ident[Parsing, String]))
)
.andThen(readInt.split(readInt).split(readInt))
.andThen(
parsingSMC
.assocr[Int, Int, Int]
.andThen(parsingSMC.assocl[Int, Int, Int])
.andThen(parsingSMC.swap[Int, Int].split(ident[Parsing, Int]))
.andThen(parsingSMC.assocr[Int, Int, Int])
.andThen(ident[Parsing, Int].split(parsingSMC.swap[Int, Int]))
.andThen(parsingSMC.assocl[Int, Int, Int])
.andThen(parsingSMC.swap[Int, Int].split(ident[Parsing, Int]))
)
.andThen(date)Volga
...leads to a lot more operations
val parseDateTime: Parsing[String, LocalDateTime] = parsing { (s: V[String]) =>
val (dayStr, rest1) = sep(".")(s)
val (monthStr, rest2) = sep(".")(rest1)
val (yearStr, rest3) = sep(" ")(rest2)
val (hourStr, rest4) = sep(":")(rest3)
val (minuteStr, secondStr) = sep(":")(rest4)
----
val year = readInt(yearStr)
val month = readInt(monthStr)
val day = readInt(dayStr)
val hour = readInt(hourStr)
val minute = readInt(minuteStr)
val second = readInt(secondStr)
----
val d = date(day, month, year)
val t = time(hour, minute, second)
dateTime(d, t)
}Volga
complex logic
val parseDateAndTimeManual =
sep(".")
.andThen(ident[Parsing, String].split(sep(".")))
.andThen(
parsingSMC.assocl[String, String, String].andThen(parsingSMC.swap[String, String].split(ident[Parsing, String]))
)
.andThen(ident[Parsing, (String, String)].split(sep(" ")))
.andThen(
ident[Parsing, (String, String)]
.split(ident[Parsing, (String, String)])
.andThen(parsingSMC.assocr[String, String, (String, String)])
.andThen(
ident[Parsing, String]
.split(
parsingSMC
.assocl[String, String, String]
.andThen(
parsingSMC
.swap[String, String]
.split(ident[Parsing, String])
)
.andThen(parsingSMC.assocr[String, String, String])
)
)
.andThen(parsingSMC.assocl[String, String, (String, String)])
.andThen(parsingSMC.swap[String, String].split(ident[Parsing, (String, String)]))
.andThen(parsingSMC.assocl[(String, String), String, String])
)
.andThen(ident[Parsing, Tuple2[Tuple2[String, String], String]].split(sep(":")))
.andThen(
parsingSMC
.assocr[(String, String), String, (String, String)]
.andThen(parsingSMC.assocr[String, String, (String, (String, String))])
.andThen(
ident[Parsing, String]
.split(
parsingSMC
.assocl[String, String, (String, String)]
.andThen(ident[Parsing, (String, String)].split(ident[Parsing, (String, String)]))
.andThen(parsingSMC.assocr[String, String, (String, String)])
.andThen(
ident[Parsing, String]
.split(
parsingSMC
.assocl[String, String, String]
.andThen(
parsingSMC
.swap[String, String]
.split(ident[Parsing, String])
)
.andThen(parsingSMC.assocr[String, String, String])
)
)
.andThen(parsingSMC.assocl[String, String, (String, String)])
.andThen(parsingSMC.swap[String, String].split(ident[Parsing, (String, String)]))
.andThen(parsingSMC.assocr[String, String, (String, String)])
)
)
.andThen(parsingSMC.assocl[String, String, (String, (String, String))])
.andThen(parsingSMC.assocl[(String, String), String, (String, String)])
.andThen(parsingSMC.assocl[((String, String), String), String, String])
)
.andThen(ident[Parsing, (((String, String), String), String)].split(sep(":")))
.andThen(
parsingSMC
.assocr[((String, String), String), String, (String, String)]
.andThen(parsingSMC.assocr[(String, String), String, (String, (String, String))])
.andThen(parsingSMC.assocr[String, String, (String, (String, (String, String)))])
.andThen(
ident[Parsing, String]
.split(
parsingSMC
.assocl[String, String, (String, (String, String))]
.andThen(
parsingSMC
.swap[String, String]
.split(ident[Parsing, (String, (String, String))])
)
.andThen(parsingSMC.assocr[String, String, (String, (String, String))])
.andThen(
ident[Parsing, String]
.split(
parsingSMC
.assocl[String, String, (String, String)]
.andThen(
parsingSMC
.swap[String, String]
.split(ident[Parsing, (String, String)])
)
.andThen(parsingSMC.assocr[String, String, (String, String)])
)
)
.andThen(parsingSMC.assocl[String, String, (String, (String, String))])
.andThen(ident[Parsing, (String, String)].split(ident[Parsing, (String, (String, String))]))
.andThen(parsingSMC.assocr[String, String, (String, (String, String))])
)
)
.andThen(parsingSMC.assocl[String, String, (String, (String, (String, String)))])
.andThen(parsingSMC.assocl[(String, String), String, (String, (String, String))])
.andThen(parsingSMC.assocl[((String, String), String), String, (String, String)])
.andThen(parsingSMC.assocl[(((String, String), String), String), String, String])
)
.andThen(
readInt
.split(readInt)
.split(readInt)
.split(readInt)
.split(readInt)
.split(readInt)
)
.andThen(
parsingSMC
.assocr[(((Int, Int), Int), Int), Int, Int]
.andThen(parsingSMC.assocr[((Int, Int), Int), Int, (Int, Int)])
.andThen(parsingSMC.assocr[(Int, Int), Int, (Int, (Int, Int))])
.andThen(parsingSMC.swap[Int, Int].split(ident[Parsing, (Int, (Int, (Int, Int)))]))
.andThen(parsingSMC.assocr[Int, Int, (Int, (Int, (Int, Int)))])
.andThen(
ident[Parsing, Int]
.split(
parsingSMC
.assocl[Int, Int, (Int, (Int, Int))]
.andThen(parsingSMC.swap[Int, Int].split(ident[Parsing, (Int, (Int, Int))]))
.andThen(parsingSMC.assocr[Int, Int, (Int, (Int, Int))])
)
)
.andThen(parsingSMC.assocl[Int, Int, (Int, (Int, (Int, Int)))])
.andThen(parsingSMC.swap[Int, Int].split(ident[Parsing, (Int, (Int, (Int, Int)))]))
.andThen(parsingSMC.assocr[Int, Int, (Int, (Int, (Int, Int)))])
.andThen(
ident[Parsing, Int]
.split(
ident[Parsing, Int]
.split(
ident[Parsing, Int]
.split(parsingSMC.assocl[Int, Int, Int])
)
)
)
.andThen(parsingSMC.assocl[Int, Int, (Int, ((Int, Int), Int))])
.andThen(parsingSMC.assocl[(Int, Int), Int, ((Int, Int), Int)])
)
.andThen(date.split(time))
.andThen(dateTime)Volga
...undoable by hand
146 operations
val parseDate1: Parsing[String, LocalDate] = parsing { (s: V[String]) =>
val (dayStr, monthYear) = SMCSyn(sep(".")).apply(s)
val (monthStr, yearStr) = SMCSyn(sep(".")).apply(monthYear)
----
val year = SMCSyn(readInt).apply(yearStr)
val month = SMCSyn(readInt).apply(monthStr)
val day = SMCSyn(readInt).apply(dayStr)
SMCSyn(date).apply(day, month, year)
}Volga
Syntactic extensions
val parseDate1: Parsing[String, LocalDate] = parsing { (s: V[String]) =>
val (dayStr: V[String], monthYear: V[String]) = SMCSyn(sep(".")).apply(s)
val (monthStr: V[String], yearStr: V[String]) = SMCSyn(sep(".")).apply(monthYear)
----
val year: V[Int] = SMCSyn(readInt).apply(yearStr)
val month: V[Int] = SMCSyn(readInt).apply(monthStr)
val day: V[Int] = SMCSyn(readInt).apply(dayStr)
SMCSyn(date).apply(day, month, year)
}
Volga
Type inference.
Available in your favorite IDE today
Related works
Related works
- Purity
- Totality
- Linear-like type system
- Tagless Final Friendly
Symmetric Monoidal Category
- Do not require function lifting
- Exactly one use , except unit type
- Reactive streams
- Distributed, session types, code mobility
- Serverless
- Linear algebra, computation graphs, auto-differentiation
- Database languages
- Business rules
- (Co)effects
Symmetric Monoidal Category
use cases
trait Symon[->[_, _], x[_, _], I]{
def id[A]: A -> A
def compose[A, B, C](f: B -> C, g: A -> B): A -> C
def tensor[A, B, C, D](f: A -> C, g: B -> D): (A x B) -> (C x D)
def assocl[A, B, C]: (A x (B x C)) -> ((A x B) x C)
def swap[A, B]: (A x B) -> (B x A)
def lunit[A]: (I x A) -> A
def unitl[A]: A -> (I x A)
}Symmetric Monoidal Category
Questions
email: odomontois@gmail.com, o.nizhnikov@tinkoff.ru
telegram: @odomontois
Composition of arrows and SMC
By Oleg Nizhnik
