Parametric polymorphism in scala:
Generics and HKT
Parametric polymorphism in scala:
Generics and HKT
Plan
- Simple slides
- Not so simple slides
- Exercises
- Uncomfortably not simple slides
During slides write your guess to ms teams chat (or shout)
val numbers: String = "1 2 3 4 5"
def foo(x: Data): Oolong = None
case class Data(name: String, age: Int)
Recap: Types
case class Data(...)
sealed trait HardToUseData
List[String]
type Oolong = Option[Long]
Recap: Types
val a = 1
def foo(b: Int) = {
val c = a + b
}Functions
case class A()
def foo[B](f: A => B) = {
val x: B = f(A())
}
Generic Functions
case class Pair[A, B](first: A, second: B)
def toList[A](pair: Pair[A, A]): List[A] = {
val x: A = pair.first
val y: A = pair.second
List(x, y)
}
Generics Types
List[+A]
Vector[+A]
Set[A]
Map[K, +V]
Generic collections
case class Triple[A](first: A, second: A, third: A){
def map[B](f: A => B): Triple[B] = {
val x: B = f(first: A)
val y: B = f(second: A)
val z: B = f(third: A)
Triple(x, y, z)
}
}Generic scopes
Parametric Polymorphism
- 2-nd order logic / System F, J.-Y. Girard(1972), J. C. Reynolds(1974)
-
ML, R. Milner, since 1975 (programming language with PP and type inference)
-
Haskell, since 1990, S. Peyton-Jones, P. Wadler etc. (2-nd order PP, HKT, Type-classes)
-
System F<:, 1990-s, L. Cardelli., S.Martini, J.C.Mitchell,
-
Generic Java 1999, M.Odersky et al (java extension with PP, type bounds)
-
Scala, since 2004, M.Odersky (type bounds, variance, HKT, implicits)
Generics
Universal representation
(everything is a reference )
- Ocaml
- Haskell (?)
- Java
- Typescript
-
Scala
Generic structures
(value types)
- C#
- Rust
- Swift
- Go
Type Erasure
Type Parameters Relevance
Irrelevant
- Ocaml
- Haskell (?)
- Java
- Typescript
-
Scala
- Rust (?)
- Go
- Swift
Relevant
- C#
- C++
Type Parameters
def foo[A, B](x: List[A]): Option[B]
~
foo: (A: Type, B: Type) => (x: List[A]) => Option[B]class Foo[A, B](x: List[A], y: Option[B])
Foo : (A: Type, B: Type) => TypeSubtyping
abstract class Animal
class Cat extends Animal
class Dog extends Animal[Cat <: Animal]
[Dog <: Animal]
[Cat ? Dog]Barbara Liskov Substitution Principle:
Let ϕ ( x ) be a property provable about objects x of type T.
Then ϕ ( y ) should be true for objects y of type S where S is a subtype of T.
Everything that is known about elements of supertype should apply to elements of subtype
Apply Carefully !!!!!!!!!!!!
case class Triple[A <: Animal](first: A, second: A, third: A)
Triple(1, 2, 3) // Compile Error!!!
Triple(cat, dog, cat) // OkGeneric Upper Bounds
case class Triple[A](first: A, second: A, third: A){
def withFirst[A1 >: A](x: A1): Triple[A1] =
Triple(x, second, third)
}Generic Lower Bounds
case class Triple[A](...)
~
case class Triple[A >: Nothing <: Any]Double Bounds
def foo[A >: Dog <: Animal] // implies Dog <: Animal
def foo[A >: Dog <: Cat] // TYPE ERROR !!!!Subtyping
abstract class Animal
class Cat extends Animal
class Dog extends Animal[Cat <: Animal]
[Dog <: Animal]
[Cat ? Dog]Covariant
F[+_]
A <: BF[A] <: F[B]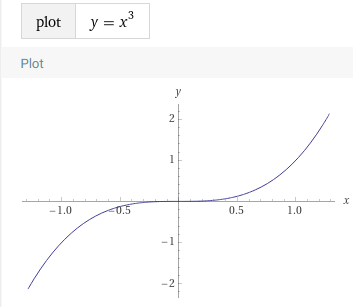
sealed trait List[+A]
sealed trait Vector[+A]
sealed trait Map[K, +V]
type Function1[-A, +B]
sealed trait IO[+A]
sealed trait ZIO[-R, +E, +A]Covariant
F[+_]
def dog: Dog
def cat: Cat
val dogs = List(dog)
val cats = List(cat)
val animals = List(cat, dog)
val nothing = List()
val anything = List(1, "1")dogs : List[Animal]
cats : List[Animal]
animals: List[Animal]
nothing: List[Animal]
anything: List[Animal]
dogs: List[Dog]
cats: List[Dog]
animals: List[Dog]
nothing: List[Dog]
anything: List[Dog]
dogs: List[Cat]
cats: List[Cat]
animals: List[Cat]
nothing: List[Cat]
anything: List[Cat]
Contravariant
F[-_]
A <: BF[A] >: F[B]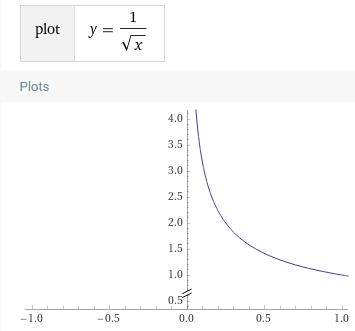
trait Consumer[-A]
type Function2[-A, -B, +R]
sealed trait ZIO[-R, +E, +A]Contravariant
F[-_]
trait Says[-A]{
def say(a: A): String
}
// Says[-A] = A => String
val dogSays: Says[Dog] =
_ => "Woof"
val catSays: Says[Cat] =
_ => "Meow"
val animalSays: Says[Animal] = {
case _ : Cat => "I'm a cat"
case _ : Dog => "I'm a dog"
}
val anyoneSays: Says[Any] =
_ => "I am"
val nooneSays: Says[Any] =
_ => "Scala is so easy to learn"val catSays: Says[Animal]
val dogSays: Says[Animal]
val animalSays: Says[Animal]
val anyoneSays: Says[Animal]
val nooneSays: Says[Animal]
val catSays: Says[Dog]
val dogSays: Says[Dog]
val animalSays: Says[Dog]
val anyoneSays: Says[Dog]
val nooneSays: Says[Dog]
val catSays: Says[Cat]
val dogSays: Says[Cat]
val animalSays: Says[Cat]
val anyoneSays: Says[Cat]
val nooneSays: Says[Cat]Contravariant
F[-_]
trait Says[-A]{
def say(a: A): String
}
// Says[-A] = A => String
val dogSays: Says[Dog] =
_ => "Woof"
val catSays: Says[Cat] =
_ => "Meow"
val animalSays: Says[Animal] = {
case _ : Cat => "I'm a cat"
case _ : Dog => "I'm a dog"
}
val anyoneSays: Says[Any] =
_ => "I am"
val nooneSays: Says[Nothing] =
_ => "Scala is so easy to learn"val catSays: Says[Animal]
val dogSays: Says[Animal]
val animalSays: Says[Animal]
val anyoneSays: Says[Animal]
val nooneSays: Says[Animal]
val catSays: Says[Dog]
val dogSays: Says[Dog]
val animalSays: Says[Dog]
val anyoneSays: Says[Dog]
val nooneSays: Says[Dog]
val catSays: Says[Cat]
val dogSays: Says[Cat]
val animalSays: Says[Cat]
val anyoneSays: Says[Cat]
val nooneSays: Says[Cat]Composition
F[+G[+_]]
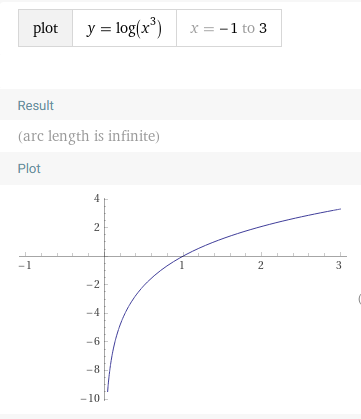
type Matrix[+A] = Vector[Vector[A]]
type Results[+A] = IO[List[A]]Composition
F[+G[-_]]
type Consumers[-A] = List[Consumer[A]]
type ShowWithPrefix[-A] =
String => (A => String)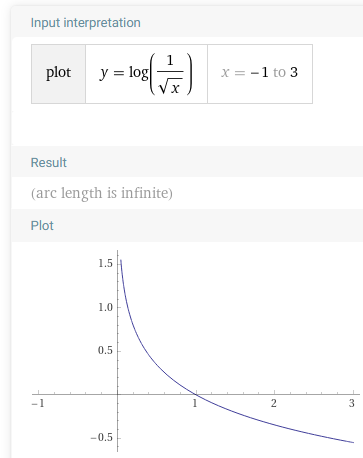
Composition
F[-G[-_]]
type Task[+A] = (A => Unit) => Unit
HKT
class Couple[A](x: A, y: A)
Couple : (A: Type) => TypeHigher Kinded Type parameters
case class ListAndOption[A, B](x: List[A], y: Option[B])
ListAndOption : (A: Type, B: Type) => Typecase class FPair[F[_], G[_], A, B](x: F[A], G[A])
type ListAndOption[A, B] = FPair[List, Option, A, B]Higher Kinded Type parameters
case class Compose[F[+_], G[+_], +A](value: F[G[A]])
type IntFunction[+A] = Int => A
type Matrix[+A] = Compose[Vector, Vector, A] // value: Vector[Vector[A]]
type BinaryIntFunction =
Compose[IntFunction, IntFunction, Int] // value: Int => Int => IntKind
Animal // // *
Set[A] // [_] // * -> *
List[+A] // [+_] // + -> *
Pair[A, B] // [_, _] // * -> * -> *
Function[-A, +B] // [-_, +_] // - -> + -> *
Fix[F[_]] // [_[_]] // (* -> *) -> *
Free[F[_], A] // [_[_], _] // (* -> *) -> * -> *
Iteratee[F[+_], -A, +R] // [_[+_], -_, +_] // (+ -> *) -> - -> + -> *
Zoo[+X <: Animal] // [+_ <: Animal]
Food[-X >: Animal] // [-_ >: Animal]
Kind = Type of Types
Subtyping and Bounds
F[_] <: G[_] iff for all A : F[A] <: G[A]
def flatten[F[x] <: Iterable[x], A](fx: F[F[A]]): F[A] = ???
class Collection[Get[x] >: (Int => x), A](get: Get[A])Subkinding
[+_] <: [_]
[-_] <: [_]
[F[+_]] >: [F[_]]
[F[-_]] >: [F[_]]
[_] <: [_ >: A <: B] // A <: B
//when A1 >: A and B1 <: B
[_ >: A1 <: B1] <: [_ >: A <: B]Kind = Type of Types
Type Lambdas
sealed trait Free[+F[+_], +A]
type IntPair[+A] = (Int, A)
type IntStream[B] = Free[IntPair, B]
type Stream[A, B] = Free[???, B]
type Stream[A, B] = Free[(A, *), B]
Type Lambdas
type Stream[A, B] = Free[(A, *), B]
type FancyParser[A, B] = Nested[A => *, Either[String, *], B]
type FanciestParser[-A, +B] = Compose[A => +*, Either[String, +*], B]
type Pair[+A] = (A, A)
type BinaryTree[A] = Free[Lambda[x => (x, x)], A]
type Four[A] = Compose[Lambda[`+x` => (x, x)], Lambda[`+x` => (x, x)], A]
Either[String, *] ~ ({type L[A] = Either[String, A]})#LScala 3 Type Lambdas
type Stream[A, B] = Free[[x] =>> (A, x), B]
type FancyParser[A, B] =
Nested[[x] =>> A => x, [x] =>> Either[String, x], B]
type FanciestParser[-A, +B] =
Compose[[x] =>> A => x, [x] =>> Either[String, x], B]
type Pair[+A] = (A, A)
type BinaryTree[A] = Free[[x] =>> (x, x), A]
type Four[A] = Compose[[x] =>> (x, x), [x] =>> (x, x), A]

SUB or SUPER
HKT
By Oleg Nizhnik
HKT
- 925


