Cálculo Multivariable
Unidad 2: Cálculo Diferencial de las Funciones de Varias Variables.
Ing. Oscar Alonso Rosete Beas
Semana 12 Octubre Rev:2 ciclo 2020-2
oscarrosete.com
oscarrosete.com

Agenda
2.1 Planteamiento de problemas que involucran más de una variable independiente.
2.2 Derivación parcial, diferenciales de funciones multivariadas y diferencial total.
2.3 Coordenadas cilíndricas, esféricas y jacobianos.
2.4 Máximos, mínimos y puntos silla.
2.5 Método de multiplicadores de Lagrange.
Unidad 2: Cálculo Diferencial de las Funciones de Varias Variables.
oscarrosete.com
Unidad 2
oscarrosete.com

Agenda
oscarrosete.com

oscarrosete.com
06/10
2.1 Planteamiento de problemas que involucran más de una variable independiente.
2.2 Derivación parcial, diferenciales de funciones multivariadas y diferencial total.
2.3 Coordenadas cilíndricas, esféricas y jacobianos.
2.4 Máximos, mínimos y puntos silla.
2.5 Método de multiplicadores de Lagrange.
Unidad 2: Cálculo Diferencial de las Funciones de Varias Variables.
Ejercicios tarea

oscarrosete.com
Halle las dos derivadas parciales de primer orden de las siguientes funciones
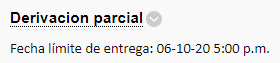
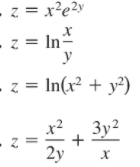
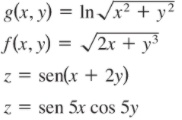
Seleccione dos de estas funciones y compruebe el teorema de las derivadas mixtas.
06/10
Notación para las primeras derivadas parciales

oscarrosete.com

"Se lee como la derivada parcial de ff con respecto a xx"
06/10
Ejercicio final

oscarrosete.com
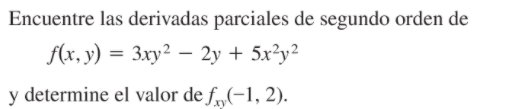
06/10
Ejemplo de aplicación

oscarrosete.com

Una medida de la percepción del calor ambiental para una persona promedio es el índice de temperatura aparente. Un modelo para este índice es
donde A es la temperatura aparente en grados Celsius, t es la temperatura del aire y h es la humedad relativa dada en forma decimal. Fuente: The UMAP Journal.
si t=30 y h=0.8
¿Qué influye mas sobre A, la temperatura del aire o la humedad?
06/10
Diferencial total

oscarrosete.com
06/10
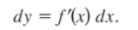
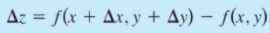
En una funcion dada y=f(x) se definió la diferencial de y como
Terminologia similar se utiliza para una función de dos variables z=f(x,y).
Δx y Δy son los incrementos x, y , y el incremento en z esta dado por
Diferencial total

oscarrosete.com
06/10

Aproximación mediante diferenciales

oscarrosete.com
06/10
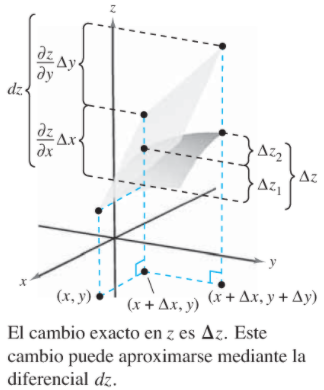
Si se elige (x+Δ, y+Δ) suficientemente cerca de (x,y) se puede usar la aproximación.
Para determinar el cambio exacto en z=Δz, se establece que este valor se aproxima a dz (la diferencial total), denominada aproximación lineal.
Ejemplo aplicación

oscarrosete.com
06/10
Un productor de bienes y servicios determino que la función de producción de su bien A está dado por:
Donde k es el capital en miles de dolares y L es la fuerza laboral en horas-hombre.
Si el productor posee inicialmente 2000 dolares de capital y 1024 horas hombre para la producción inicla del bien.
Calcule la variación en la producción inicial si se desea aumentar el capital inicial en 100 dolares y disminuir la fuerza laboral inicia en 2 horas hombre.
Ejercicios

oscarrosete.com
En los ejercicios evalue f(2,1) y f (2.1,1.05) y calcule Δz, use la diferencial total dz para aproximar Δz.


06/10
Referencia adicional
oscarrosete.com
06/10
Ejemplo aplicación diferencial total

oscarrosete.com
08/10
El radio de la base y la altura de un cono circular recto se miden como 10 cm y 25 cm, respectivamente, con un posible error de medición de hasta 0.1 cm en cada uno. Use diferenciales para estimar el error máximo en el volumen calculado del cono.
Funciones de tres o más variables

oscarrosete.com
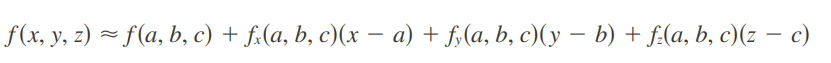
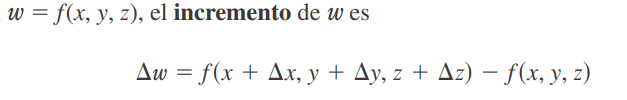
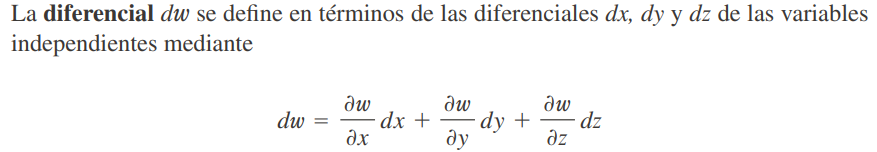
08/10
Funciones de tres o más variables

oscarrosete.com
Las dimensiones de una caja rectangular se miden en 75 cm, 60 cm y 40 cm y cada medida es correcta con un margen de error de 0.2 cm. Use diferenciales para estimar el mayor error posible cuando el volumen de la caja se calcula a partir de estas medidas.
08/10
Regla de la cadena

oscarrosete.com

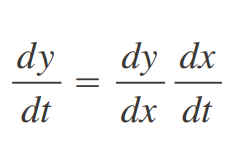
Para funciones con más de una variable, la regla de la cadena tiene varias versiones, cada una de las cuales da una regla para derivar una función compuesta. La primera versión (teorema 2) se refiere al caso donde z=f(x, y) y cada una de las variables x y y es a su vez una función de una variable t. Esto significa que z es indirectamente una función de t, z= f(g(t),ht(t))
08/10
Regla de la cadena

oscarrosete.com
z es indirectamente una función de t, z= f(g(t),ht(t))

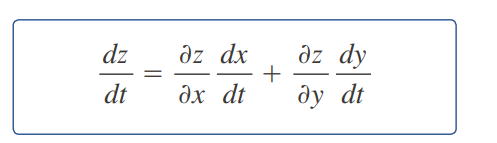
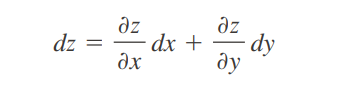
Diferencial total
Regla cadena
08/10
Ejemplo aplicación

oscarrosete.com
La presión P (en kilopascales), volumen V (en litros) y temperatura T (en grados Kelvin) de un mol de un gas ideal se relacionan por la ecuación PV=8.31T.
Determine la razón a la que cambia la presión cuando la temperatura es de 300 K y aumenta a razón de 0.1 K/s y el volumen es 100 L y aumenta a razón de 0.2 L/s.
08/10
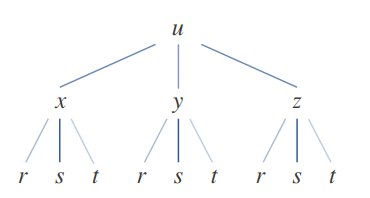
Regla de la cadena para más variables

oscarrosete.com
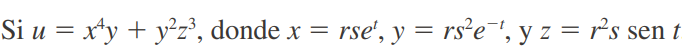
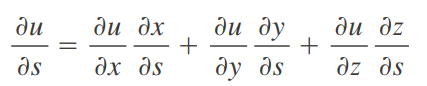
Generalmente nos podemos apoyar con un diagrama de arbol
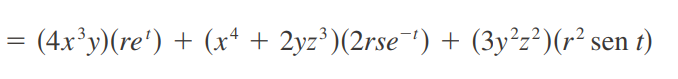
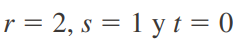
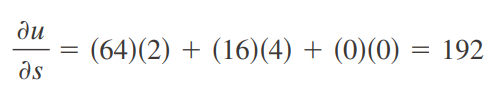
08/10

oscarrosete.com
Derivada direccional
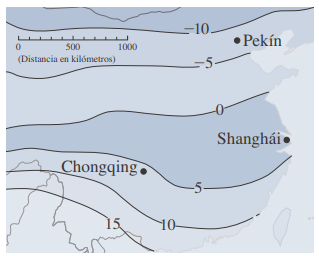
El mapa meteorológico de la figura muestra un mapa de contorno de la función de temperatura T(x,y) para China a las tres de la tarde del 28 de diciembre de 2004.
Las curvas de nivel, o isotermas, unen lugares con la misma temperatura.
La derivada parcial Tx en un lugar como Chongqing es la razón de cambio de temperatura con respecto a la distancia si se viaja al este desde Chongqing
Ty es la razón de cambio de temperatura si se viaja al norte.
08/10

oscarrosete.com

Derivada direccional
Pero, ¿y si se quiere conocer la razón de cambio de temperatura cuando se viaja al sureste o en alguna otra dirección?
Se presentará un tipo de derivada llamada derivada direccional, que permite determinar la razón de cambio de una función de dos o más variables en cualquier dirección
08/10

oscarrosete.com
Derivada direccional
si z=f(x, y), las derivadas parciales fx y fy se definen como
representan las razones de cambio de z en las direcciones de x y y, es decir en las direcciones de los vectores unitarios i y j.
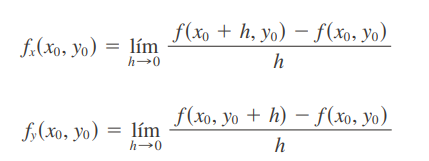
08/10

oscarrosete.com
Derivada direccional
si z=f(x, y), las derivadas parciales fx y fy se definen como
representan las razones de cambio de z en las direcciones de x y y, es decir en las direcciones de los vectores unitarios i y j.
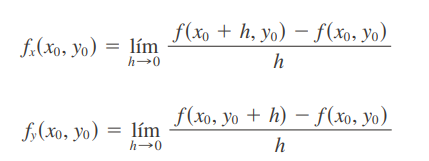
08/10

oscarrosete.com
Derivada direccional
Suponga que ahora desea determinar la razón de cambio de z en (x0,y0) en la dirección de un vector unitario arbitrario u=<a,b>.
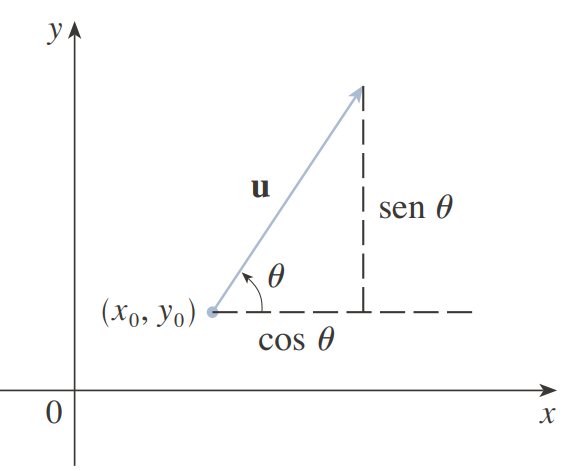
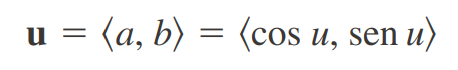
08/10

oscarrosete.com
Interpretación geométrica
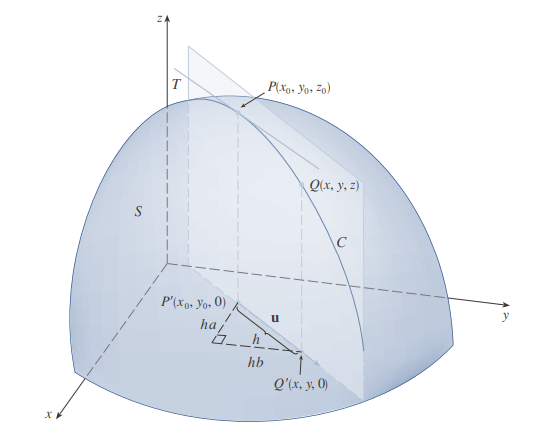
Entonces, el punto P(x0,y0,z0) reside en S. El plano vertical que pasa por P en la dirección de u interseca S en una curva C. La pendiente de la recta tangente T a C en el punto P es la razón de cambio de z en la dirección de u.
08/10

oscarrosete.com
Definición formal


08/10

oscarrosete.com
Ejemplo
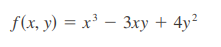
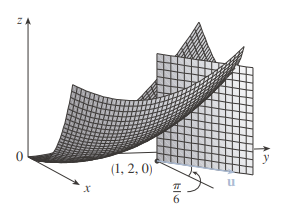
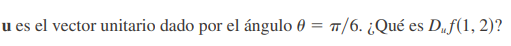
08/10

oscarrosete.com
El vector gradiente
08/10
Nótese en el teorema 3 que la derivada direccional de una función derivable puede escribirse como el producto punto de dos vectores:
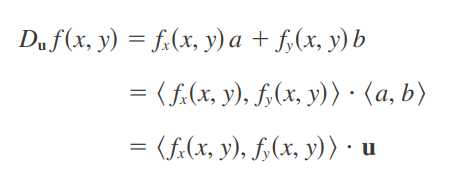
El primer vector en este producto punto no solo ocurre en el cálculo de derivadas direccionales, sino también en muchos otros contextos. Así, se le da un nombre especial (el gradiente de f) y una notación especial

oscarrosete.com
El vector gradiente
08/10
Nótese en el teorema 3 que la derivada direccional de una función derivable puede escribirse como el producto punto de dos vectores:
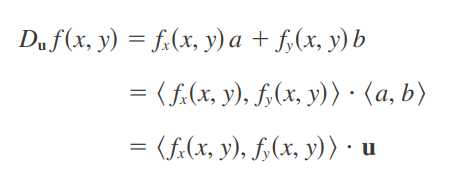
El primer vector en este producto punto no solo ocurre en el cálculo de derivadas direccionales, sino también en muchos otros contextos. Así, se le da un nombre especial (el gradiente de f) y una notación especial
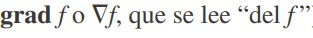

oscarrosete.com
El vector gradiente
08/10
Nótese en el teorema 3 que la derivada direccional de una función derivable puede escribirse como el producto punto de dos vectores:
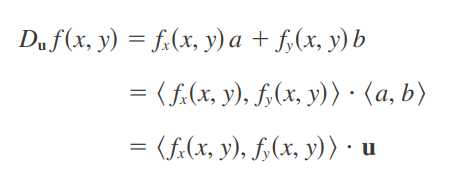
El primer vector en este producto punto no solo ocurre en el cálculo de derivadas direccionales, sino también en muchos otros contextos. Así, se le da un nombre especial (el gradiente de f) y una notación especial
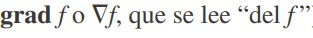

oscarrosete.com
El vector gradiente
08/10

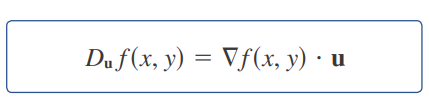
Derivada direccional reescrita

oscarrosete.com
Ejercicios alumnos
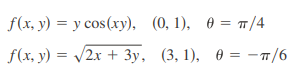
Determine la derivada direccional de f en el punto dado en la dirección indicada por el ángulo dado.

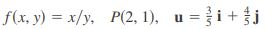
Determine el gradiente de f.
Evalúe el gradiente en el punto P.
Determine la razón de cambio de f en P en la dirección del vector u
08/10
Referencia adicional
oscarrosete.com
08/10

oscarrosete.com
Maximización de la derivada direccional
13/10
Suponga que tiene una función f de dos o tres variables y considere todas las posibles derivadas direccionales de f en un punto dado. Estas dan las razones de cambio de f en todas las direcciones posibles. Entonces, se pueden hacer estas preguntas: ¿en cuál de esas direcciones cambia más rápido f y cuál es la máxima razón de cambio?

oscarrosete.com
Maximización de la derivada direccional
13/10

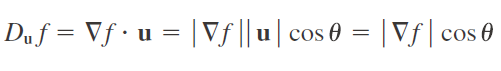


oscarrosete.com
Maximización de la derivada direccional
13/10

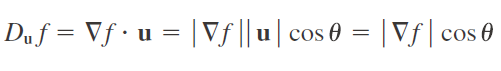
Text
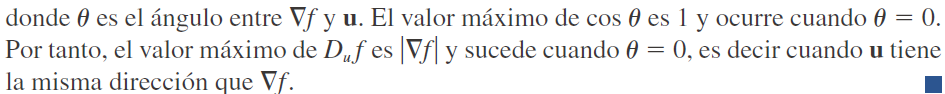

oscarrosete.com
Maximización de la derivada direccional
13/10


oscarrosete.com
Ejemplos
13/10



oscarrosete.com
Valores máximos y mínimos
13/10
Uno de los principales usos de las derivadas ordinarias es encontrar valores máximos y mínimos (valores extremos). En esta sección se verá cómo usar derivadas parciales para localizar máximos y mínimos de funciones de dos variables.

oscarrosete.com
Valores máximos y mínimos
13/10
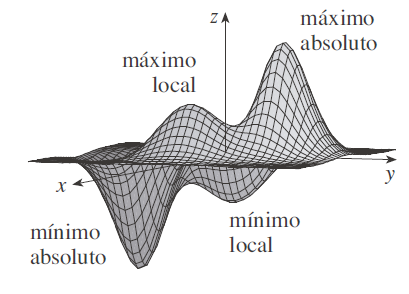
Examine las cumbres y valles de la gráfica de f que aparece en la figura. Hay dos puntos (a, b) donde f tiene un máximo local, es decir, donde (a, b) es mayor que los
valores cercanos de f(x, y). El mayor de esos dos valores es el máximo absoluto. De igual manera, f tiene dos mínimos locales, donde (a, b) es menor que los valores cercanos. El menor de estos dos valores es el mínimo absoluto.


oscarrosete.com
Valores máximos y mínimos
13/10

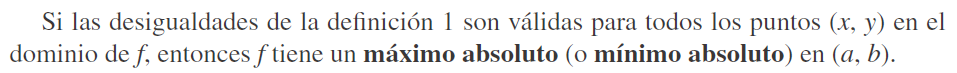
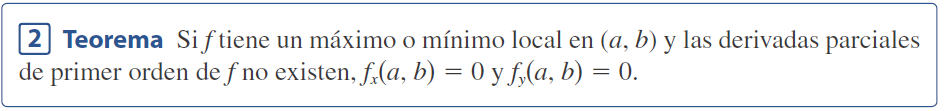
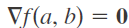
En notación del vector gradiente

oscarrosete.com
Valores máximos y mínimos
13/10
Un punto (a, b) se llama punto crítico (o punto estacionario) de f si fx(a, b)=0 y fy(a, b)=0, o si una de estas derivadas parciales no existe. El teorema 2 indica que si f tiene un máximo o mínimo local en (a, b), entonces (a, b) es un punto crítico de f.
Sin embargo, como en el cálculo de una variable, no todos los puntos críticos dan origen a máximos o mínimos. En un punto crítico, una función podría tener un máximo local o un mínimo local, o ninguno de ellos.

oscarrosete.com
Valores máximos y mínimos
13/10
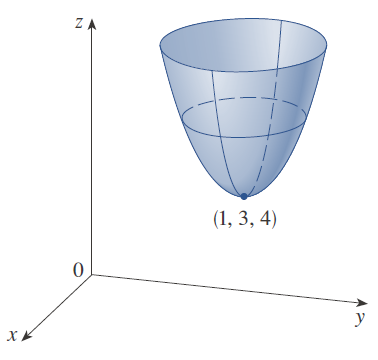
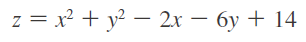
Gráfica paraboloide elíptico

oscarrosete.com
Valores máximos y mínimos
13/10
f no tiene ningún valor extremo, cerca del origen, la gráfica tiene la forma de una silla de montar, y por eso (0, 0) se llama un punto silla de f.
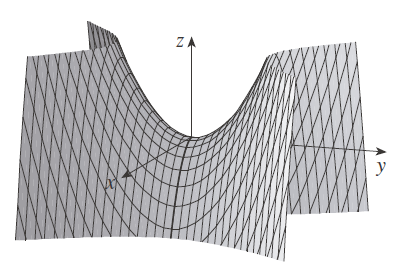
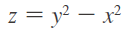

oscarrosete.com
Puntos de silla
13/10
Un paso de montaña también tiene forma de silla de montar.
Para quienes escalan en una dirección, el punto silla es el punto más bajo en su ruta, mientras que para quienes viajan en una dirección diferente el punto silla es el punto más alto.


oscarrosete.com
Prueba de la segunda derivada
13/10

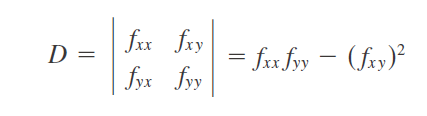
Caso c: Discriminante D<0, es un punto de silla de f
Fórmula escrita en forma de determinante:

oscarrosete.com
Criterio de la segunda derivada
13/10
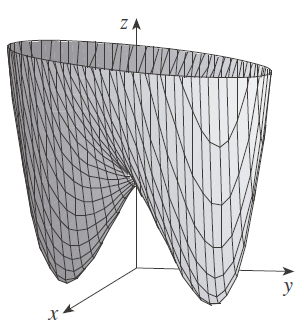
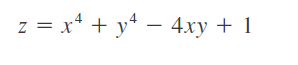
Encuentre los valores máximo y mínimo locales y los puntos silla de

oscarrosete.com
13/10
Encuentre los valores máximo y mínimo locales y los puntos silla de
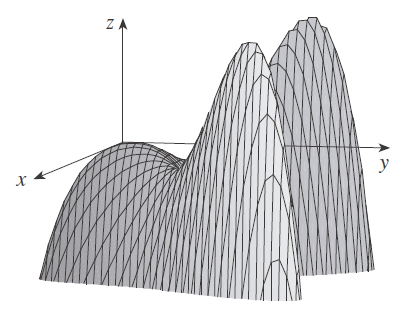
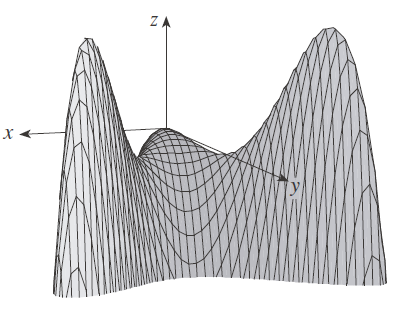
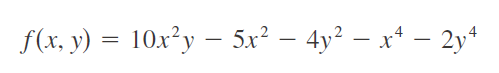
Criterio de la segunda derivada

oscarrosete.com
Valores máximos y mínimos absolutos
13/10

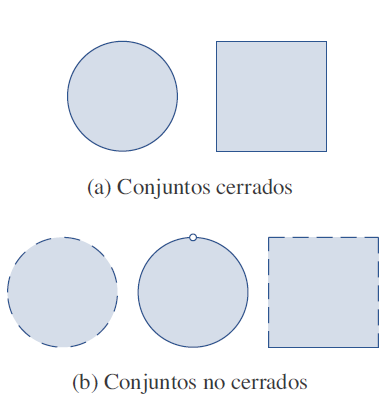

oscarrosete.com
Ejemplo ilustrativo
13/10

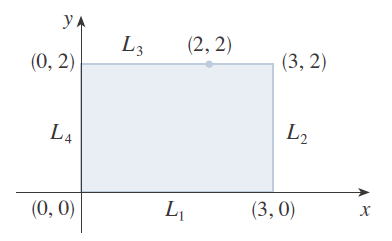

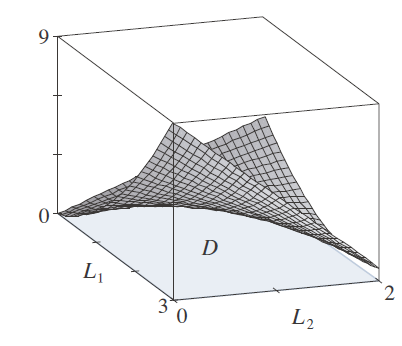

oscarrosete.com
Ejemplo de aplicación valores extremos
13/10
Una caja rectangular sin tapa debe hacerse con 12 m2 de cartón. Determine el volumen máximo de esa caja.
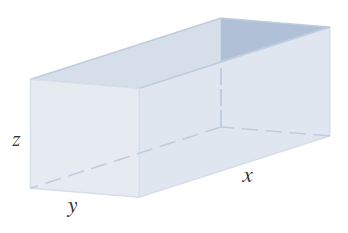

oscarrosete.com
Ejercicios alumnos
13/10
- Determine los valores máximos y mínimos locales y el punto o puntos silla de la función.
- Grafique la función con un dominio y punto de vista que revelen todos los aspectos importantes de la función.
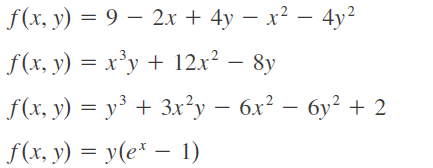
oscarrosete.com
Referencia Adicional
13/10
Calculo Multivariable Semana 12 Octubre
By Oscar Rosete
Calculo Multivariable Semana 12 Octubre
- 336