R
E
A
C
T
O
xamples
epeat
ode
pproach
ptimize
est
{Dictionary Word Finder}

The Question
Given
- An alphabetical array of dictionary entries and
- A word to search for
find and return that word's definition (if it exists).
This array of dictionary entries will be formatted like so:
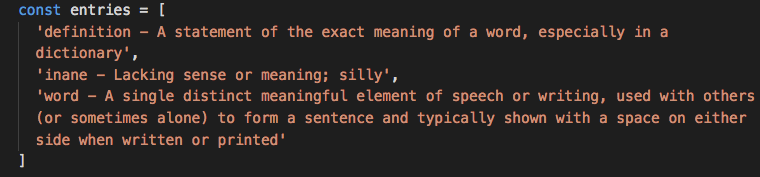
Example
insert 'a'
[ 'a' ]
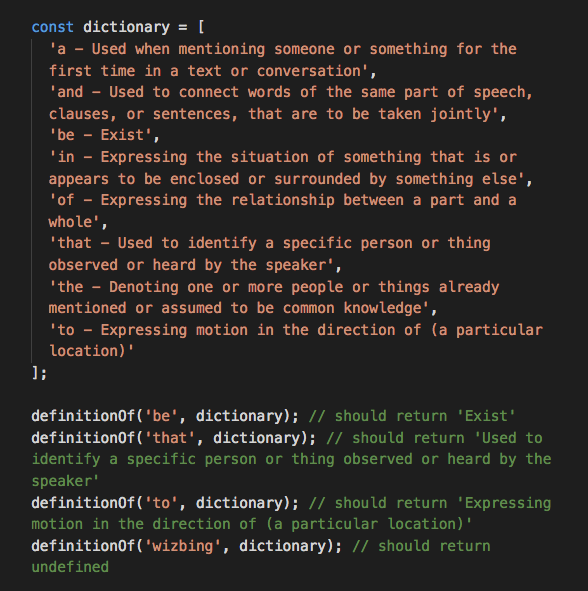
Entries are alphabetically sorted!
Naive Approach
(aka Brute Force)
insert 'a'
[ 'a' ]
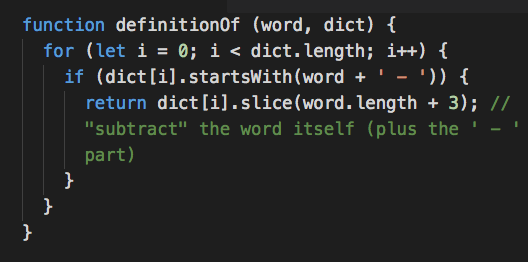
- What is the bigO time complexity?
- Space complexity?
Naive Approach
(aka Brute Force)
insert 'a'
[ 'a' ]

- O(n * m) time, where n = dict.length and m = word.length
- O(1) space
Optimized approach
insert 'a'
[ 'a' ]
What have we not taken full advantage of yet?

Optimized approach
Binary search
insert 'a'
[ 'a' ]
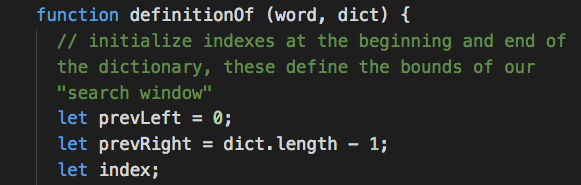
What next?
Optimized approach
Binary search
insert 'a'
[ 'a' ]


Optimized approach
Binary search
insert 'a'
[ 'a' ]
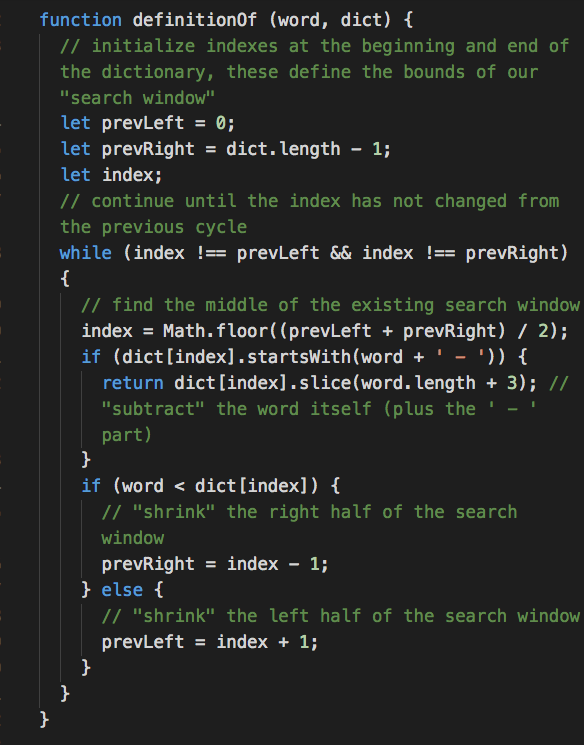
Strings compared by using > and <
O(m * log n) time
n = dict.length
m = word.length
O(1) space
Optimizing for repeated use
insert 'a'
[ 'a' ]
We usually use dictionaries more than once-
can we optimize for this use case?
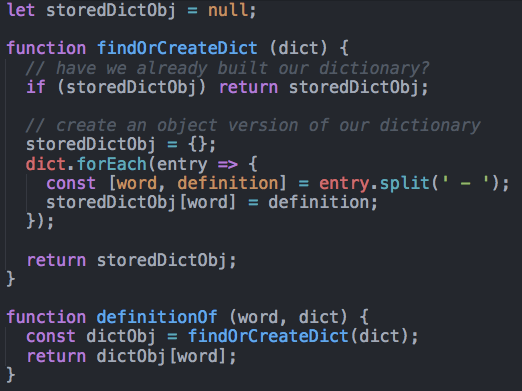
Further Optimized approach
insert 'a'
[ 'a' ]
First run: O(n) time to build dictionary object
Subsequent runs: O(1) lookup time!
O(n) space to store our dictionary object
Interviewer Tips
insert 'a'
[ 'a' ]
- If an interviewee doesn't think of the BS, point to information they are not using e.g. alphabetical order
- If that doesn't lead them to BS, ask how THEY would look for a word in a dictionary.
- If your interviewee goes down a rabbit-hole trying to implement a compareByAlphabeticalOrder function, just let them know they can use '<' and '>' to compare strings.
- If they complete BS, ask how they can optimize for repeated use- you can hint that there is a way to achieve constant lookup time.
Takeaways?
insert 'a'
[ 'a' ]
| Approach | Time complexity | Space complexity |
|---|---|---|
| Naive | O(n * m) | O(1)*** |
| Binary Search | O(m * log n) | O(1)*** |
| Hash Map | O(1) (first time O(n)) | O(n) |
What else did you learn from this problem?
What questions do you have?
n = dict.length, m = word.length
*** Might also be considered O(e), entry.length
Dictionary Word Finder
By Patrick Kim
Dictionary Word Finder
Technical interview problem on finding word definitions
- 753

