M
A
R
F
A novel neural ray field for
representing 3D shapes
Peder Bergebakken Sundt
Theoharis Theoharis
s.ntnu.no/marf
M
A
R
F
M
A
R
F
Medial
Atom
Ray
Fields
M
A
R
F
Medial
Atom
Ray
Fields
Lambertian
Single network evaluation per pixel.
(Including the normal)
Major speedup for inverse-rendering, and analysis-by-synthesis (Renders in realtime!)
MARFs improve multi-view consistency.
(Not guaranteed in ray fields)
M
A
R
F
Medial
Atom
Ray
Fields
we also get for essentially free
With our novel shape representation
M
A
R
F
Medial
Atom
Ray
Fields
Local Thickness
Unsupervised
Part Segmentation
"Approximate" Normals
We also get for essentially free:
Topological Skeleton
With our novel shape representation
M
A
R
F
Medial
Atom
Ray
Fields
Local Thickness
Subsurface Scattering
M
A
R
F
Medial
Atom
Ray
Fields
With a backward pass we show
that one can also compute
(i.e. not realtime)
M
A
R
F
Medial
Atom
Ray
Fields
True Normals
Curvature
With a backward pass we show
that one can also compute:
Despite the network
having no second derivative
(i.e. not realtime)
"Approximate" Normals
M
A
R
F
Medial
Atom
Ray
Fields
Curvature
With a backward pass we show
that one can also compute:
Despite the network
having no second derivative
"Approximate" Normals
True Normals
(i.e. not realtime)
M
A
R
F
Medial
Atom
Ray
Fields
Curvature
Anisotropic shading
(Using principal curvatures)
M
A
R
F
Medial
Atom
Ray
Fields
MARFs can represent multiple shapes
in a shared latent space
M
A
R
F
Medial
Atom
Ray
Fields
Latent space traversal
Learned from only 20 shapes
M
A
R
F
Medial
Atom
Ray
Fields
Medial atoms?
Ray Fields?
Neural Fields?
M
A
R
Medial
Atom
Ray
Fields
Medial atoms
Ray Fields
Neural Fields
MARFs
Why Neural Fields?
discrete 3D shape representations
Let's look at the shortcomings of
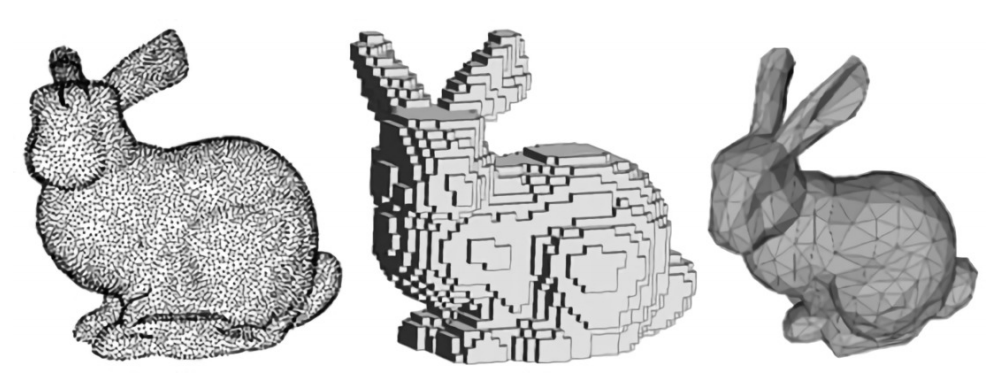
No topology,
lossy surface reconstruction.
Scales poorly
Fixed topology
or self-intersecting
... map poorly to neural networks!
Discrete 3D shape representations
Points
Voxels
Meshes
Functions mapping spatiotemporal coordinates to some quantity
Fields
Neural
... represented with a neural network
Fields
Functions mapping spatiotemporal coordinates to some quantity

Neural
Fields
- Resolution Agnostic
- Compact and scales well
- Supports any topology
- "implicit" decoder
Neural Radiance Fields - NeRF

Neural Radiance Fields - NeRF

Neural Radiance Fields - NeRF

Neural Radiance Fields - NeRF
Neural Radiance Fields - NeRF
\(\Rightarrow\) Determine the volume rendering ray integral
Differentiable Ray-Marching
3D Cartesian radiance field
\(\Rightarrow\)
Neural Radiance Fields - NeRF
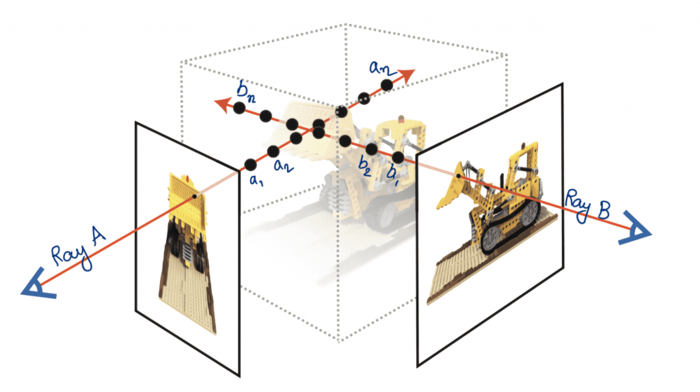
- Monte-Carlo approximation
- Requires ~100 network evaluations per ray/pixel (slow)
- Has great 3D inductive bias
- By construction
multi-view consistent
Differentiable Ray-Marching
Going faster
4 main strategies
Going faster
4 main strategies
(Offline) Tabulation
Discretization artifacts (aliasing)
Many small networks
Trade compute for memory,
loss of global shape prior
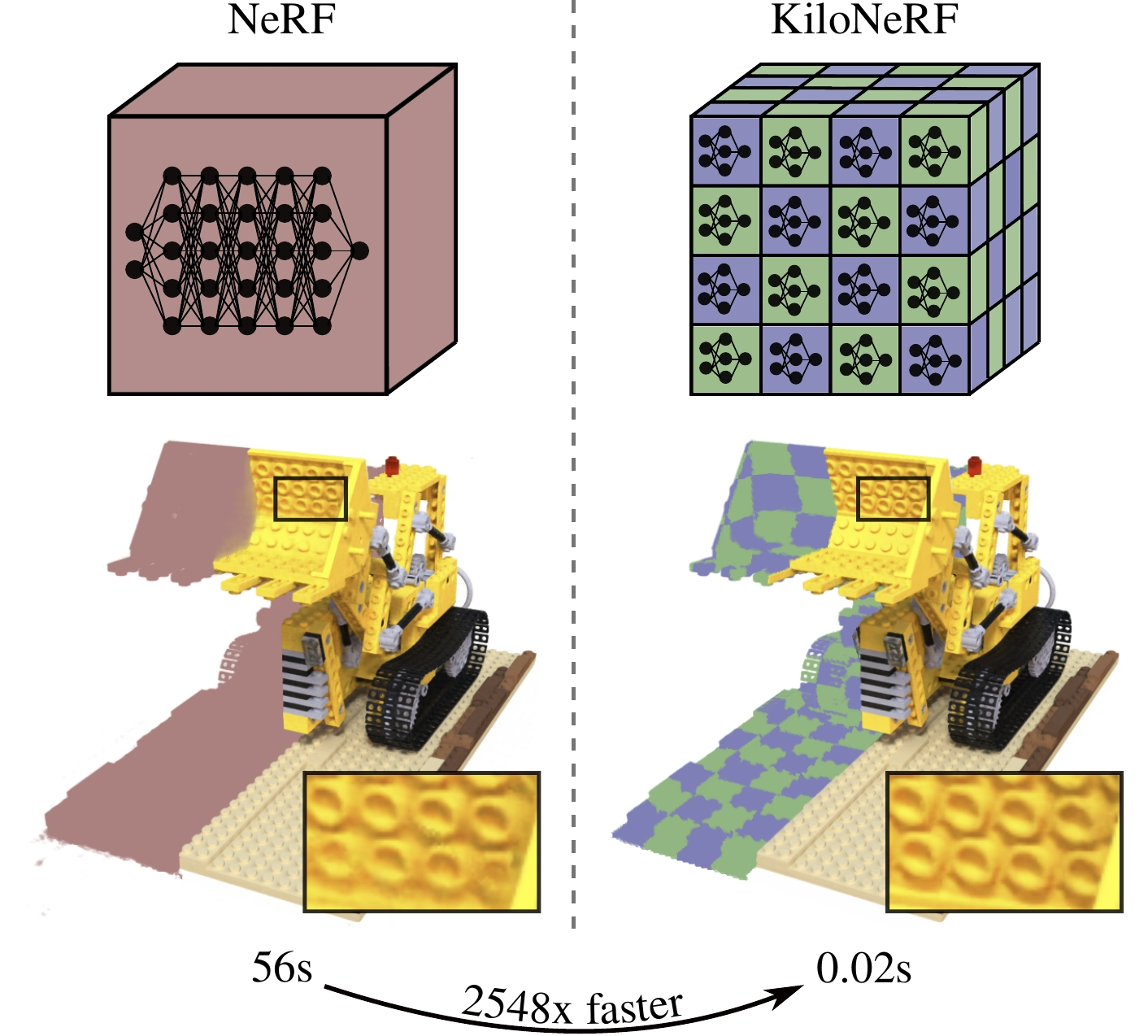
Directly predict
the ray integral

100x speedup,
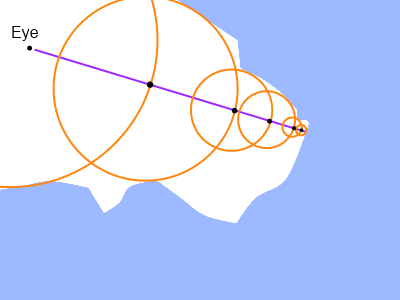
Learn a distance field
instead of density
10x speedup,
no transparency
No ray marching!
but difficult
Going faster
Directly predict
the ray integral

100x speedup,
No ray marching!
but difficult
- Not multi-view consistent
by construction (4 DoF) - No 3D inductive bias
- Not multi-view consistent
by construction (4 DoF) - No 3D inductive bias
- Not multi-view consistent
by construction (4 DoF) - No 3D inductive bias
Plücker Coordinate
No singularities
or discontinuities
No singularities
or discontinuities
Plücker Coordinate
Two prior works use this ray encoding
Plücker Coordinate
Intersection Fields
(PRIF)
Networks
Light Field
Primary Ray
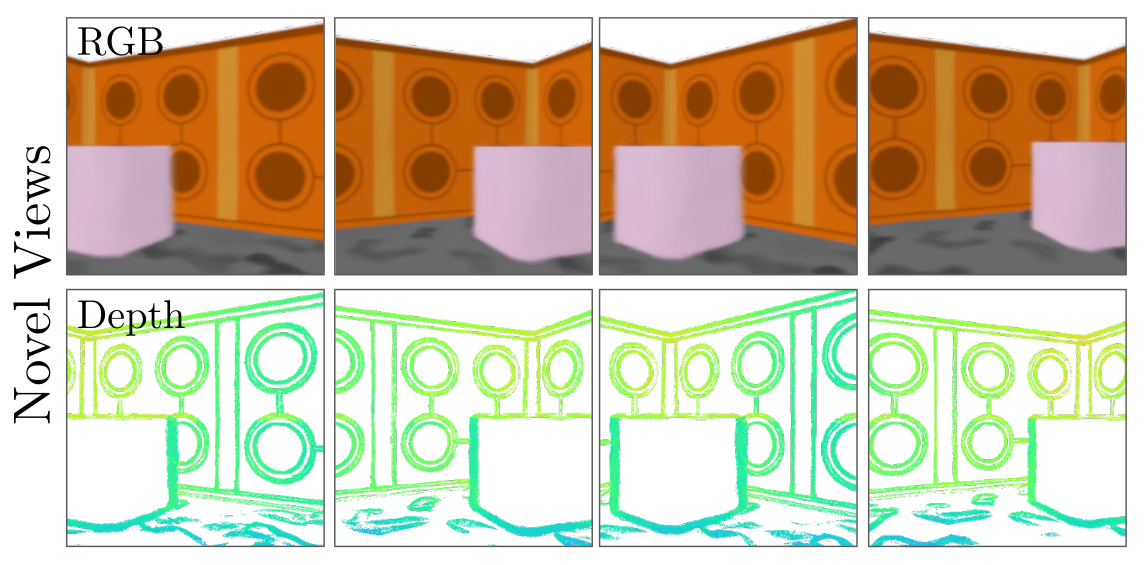

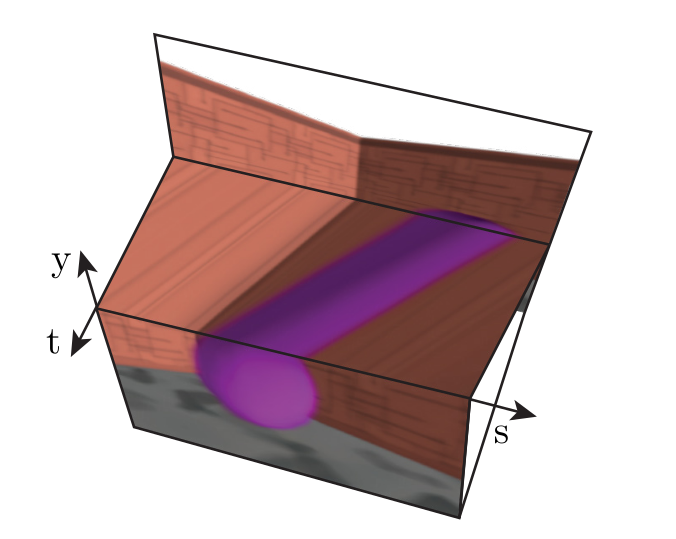
Both struggle with discontinuities!


V. Sitzmann, S. Rezchikov, W.T. Freeman, J.B. Tenenbaum, F. Durand, Light field networks: Neural scene representations with single-evaluation rendering, in: ArXiv, 2021.
B.Y. Feng, Y. Zhang, D. Tang, R. Du, A. Varshney, PRIF: Primary Ray-Based Implicit Function, in: S. Avidan, G. Brostow, M. Cissé, G.M. Farinella, T. Hassner (Eds.), Computer Vision – ECCV 2022, Springer Nature Switzerland, Cham, 2022: pp. 138–155. https://doi.org/10.1007/978-3-031-20062-5_9.
Intersection Fields
(PRIF)






Lipschitz bound!
Fuzzy edges
Requires filtering
Primary Ray
Both struggle with discontinuities!
Networks
Light Field


Intersection Fields
(PRIF)
Networks





Lipschitz bound

Light Field
Primary Ray

Intersection Fields
(PRIF)
Networks





Lipschitz bound

Light Field
Primary Ray

PRIF
Ours

We need to represent 3D shapes

Figures adapted from
D. Rebain, K. Li, V. Sitzmann, S. Yazdani, K.M. Yi, A. Tagliasacchi, Deep Medial Fields, ArXiv:2106.03804 [Cs]. (2021).


We need to represent 3D shapes
as a sum of spheres
Figures adapted from
D. Rebain, K. Li, V. Sitzmann, S. Yazdani, K.M. Yi, A. Tagliasacchi, Deep Medial Fields, ArXiv:2106.03804 [Cs]. (2021).
The Medial Axis Transform
A. Tagliasacchi, T. Delame, M. Spagnuolo, N. Amenta, A. Telea, 3D Skeletons: A State-of-the-Art Report, Computer Graphics Forum. 35 (2016) 573–597. https://doi.org/10.1111/cgf.12865.
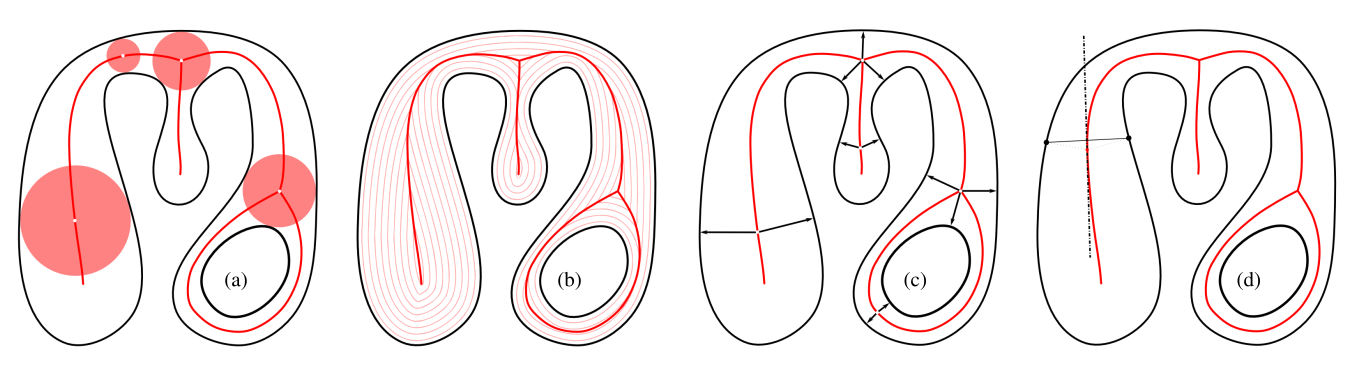



The Medial Axis Transform
Set of maximally inscribed spheres
Ridges in distance transform
Points with two+ nearest neighbors
Local axis of reflectional symmetry
Defining
A. Tagliasacchi, T. Delame, M. Spagnuolo, N. Amenta, A. Telea, 3D Skeletons: A State-of-the-Art Report, Computer Graphics Forum. 35 (2016) 573–597. https://doi.org/10.1111/cgf.12865.




The Medial Axis Transform
Set of maximally inscribed spheres
Ridges in distance transform
Points with two+ nearest neighbors
Local axis of reflectional symmetry



Defining
A. Tagliasacchi, T. Delame, M. Spagnuolo, N. Amenta, A. Telea, 3D Skeletons: A State-of-the-Art Report, Computer Graphics Forum. 35 (2016) 573–597. https://doi.org/10.1111/cgf.12865.
The Medial Axis Transform




Set of maximally inscribed spheres
Ridges in distance transform
Points with two+ nearest neighbors
Local axis of reflectional symmetry


D. Rebain, B. Angles, J. Valentin, N. Vining, J. Peethambaran, S. Izadi, A. Tagliasacchi, LSMAT Least Squares Medial Axis Transform, Computer Graphics Forum. 38 (2019) 5–18. https://doi.org/10.1111/cgf.13599.


Defining
A. Tagliasacchi, T. Delame, M. Spagnuolo, N. Amenta, A. Telea, 3D Skeletons: A State-of-the-Art Report, Computer Graphics Forum. 35 (2016) 573–597. https://doi.org/10.1111/cgf.12865.
The Medial Axis Transform




Set of maximally inscribed spheres
Ridges in distance transform
Points with two+ nearest neighbors
Local axis of reflectional symmetry


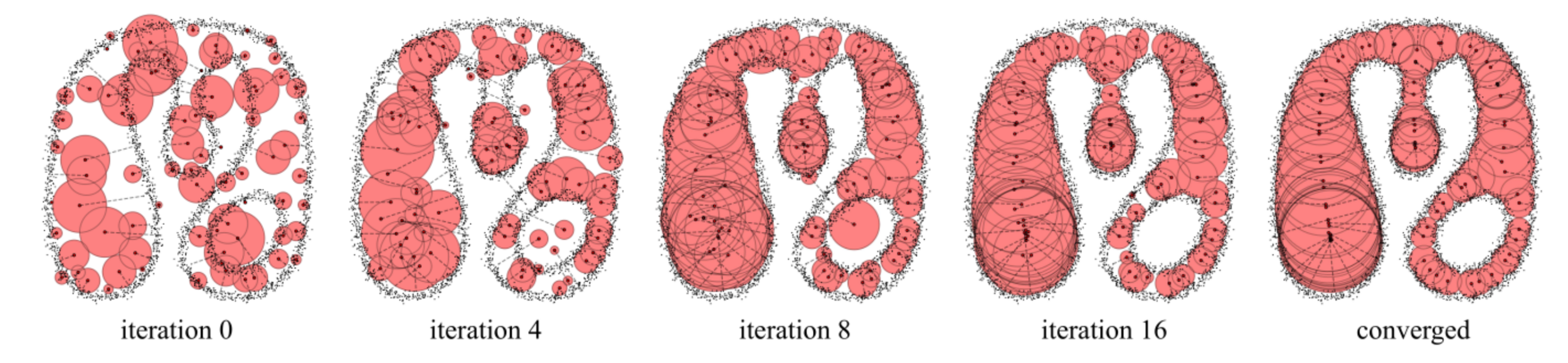




D. Rebain, B. Angles, J. Valentin, N. Vining, J. Peethambaran, S. Izadi, A. Tagliasacchi, LSMAT Least Squares Medial Axis Transform, Computer Graphics Forum. 38 (2019) 5–18. https://doi.org/10.1111/cgf.13599.
Defining
Fit for iteration
MARF
Medial Atom
Ray Field
(maximally inscribed sphere)
We propose
The Medial Atom Ray Field
Text
Medial Atom
Ray Field
MARF
We propose
The Medial Atom Ray Field
Medial Atom
Ray Field
s
MARF
We propose
The Medial Atom Ray Field
Medial Atom
Ray Field
MARF
We propose
The Medial Atom Ray Field
Medial Atom
Ray Field
MARF
We propose
The Medial Atom Ray Field
MARF
MARF
MARF
Supervising
MARF
Supervising

Training Data
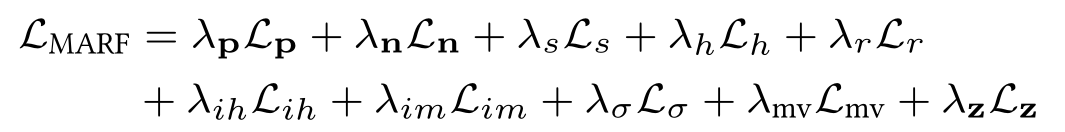
MARF
Supervising
We show the normal can be computed by
differentiating the network w.r.t. the ray,
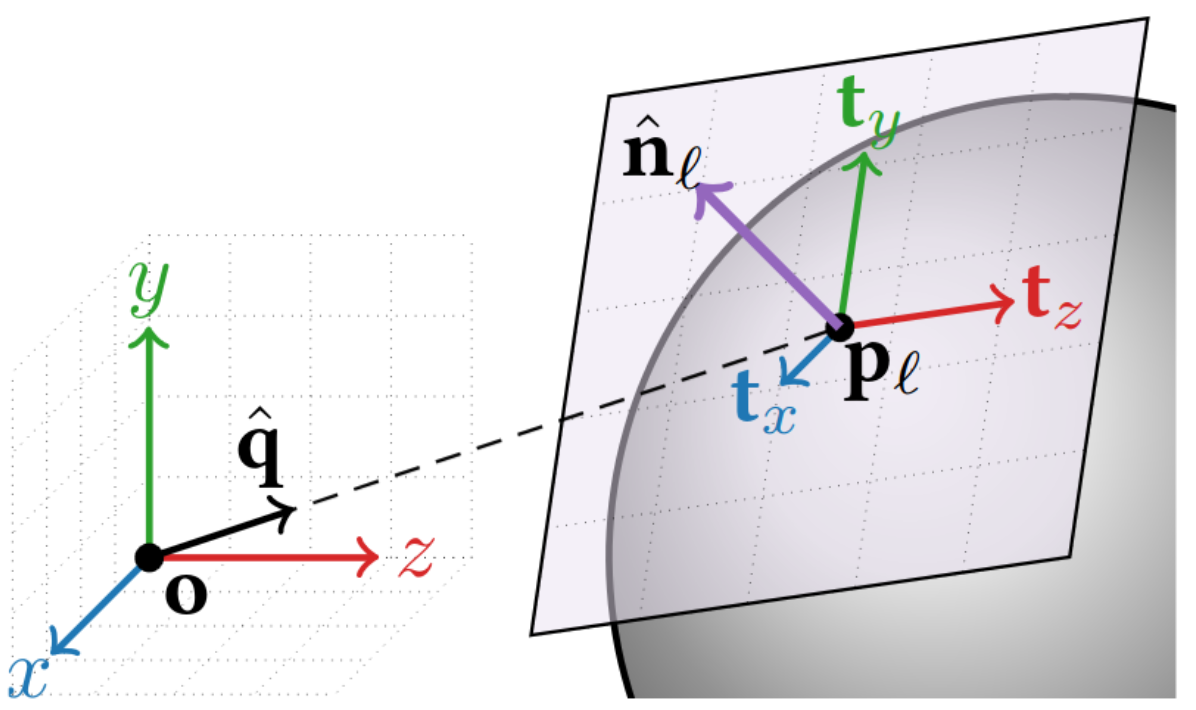

Training Data
MARF
Supervising
We show the normal can be computed by
differentiating the network w.r.t. the ray,
but its much cheaper to draw a line between the atom center and the intersection point!
MARF
Supervising
- \(=0\) if the ray should hit
- \(\gt0\) if the ray should miss
- We supervise against
precomputed ground truth

Training Data
MARF
Supervising

MARF
Supervising

MARF
Supervising

Constant positive
pressure on radius
MARF
Supervising

MARF
Supervising

MARF
Supervising

MARF
Supervising

Multi-view consistency
Observation: a point should not change w.r.t. a infinitesimal change in incident viewing angle
Supervising
Multi-view consistency

Observation: a point should not change w.r.t. a infinitesimal change in incident viewing angle

Supervising
Multi-view consistency
Observation: a point should not change w.r.t. a infinitesimal change in incident viewing angle


PRIF
Multi-view consistency
Observation: a point should not change w.r.t. a infinitesimal change in incident viewing angle



PRIF
Multi-view consistency
Observation: a point should not change w.r.t. a infinitesimal change in incident viewing angle



PRIF
MARF
Multi-view consistency
Observation: a point should not change w.r.t. a infinitesimal change in incident viewing angle


PRIF
MARF
Multi-view consistency
Observation: a point should not change w.r.t. a infinitesimal change in incident viewing angle


MARF
Multi-view consistency
Observation: a point should not change w.r.t. a infinitesimal change in incident viewing angle
PRIF
Light Fields
MARF



(Diffuse only)
Supervising
Multi-view consistency
Supervising
Multi-view consistency
Supervising
Multi-view consistency
Supervising
Multi-view consistency
Supervising
Multi-view consistency
Supervising
Multi-view consistency
Supervising
Multi-view consistency
Supervising
Multi-view consistency
Supervising
Multi-view consistency
Supervising
MARF
Ray Intersection Field
Any
Multi-view consistency
Supervising
MARF
Ray Intersection Field
Any
Multi-view consistency
Supervising
MARF
Ray Intersection Field
Any
Multi-view consistency
Supervising
Results



Results






Ours
Ground
Truth




Results






Ours
Ground
Truth



Results






Ours
Ground
Truth



Results









Ours
w/axis
Ground
Truth


















Ours
PRIF
w/axis
Ground
Truth
Results


















Ours
PRIF
w/axis
Ground
Truth
Results

















Ours
PRIF
w/axis
Ground
Truth
Results





Questions?
Thank you
s.ntnu.no/marf
s.ntnu.no/marf
skipped slides
Ray Fields
- Problem 1: Rays have 4 DoF
- \(\Rightarrow\) No multi-view consistency or 3D inductive bias!
- Problem 2: How to uniquely represent a ray?
6 DoF

3D Rigid Bodies
6 DoF

6 DoF

3 DoF
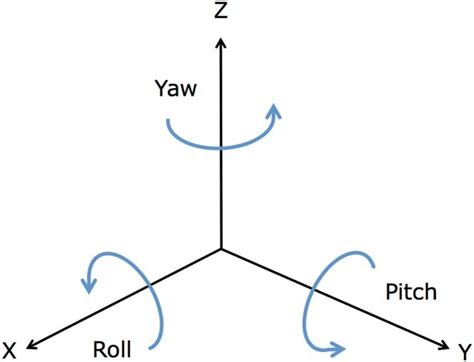
6 DoF

3 DoF
3 DoF

Compared to rigid bodies
Compared to rigid bodies
Rays loose two DoF
Rays are invariant to:
Compared to rigid bodies
Rays loose two DoF

Rotation about ray

Rotation about ray
Rays are invariant to:
Compared to rigid bodies
Rays loose two DoF
2-Sphere

Rotation about ray
Translation along ray
Rays are invariant to:
Compared to rigid bodies
Rays loose two DoF
2-Sphere

Rotation about ray
Translation along ray
Rays are invariant to:
(assuming no start)
Compared to rigid bodies
Rays loose two DoF
2-Sphere
Somehow
orthogonal
to ray

Rotation about ray
Translation along ray
Rays are invariant to:
(assuming no start)
Compared to rigid bodies
Rays loose two DoF
2-Sphere
Somehow
orthogonal
to ray
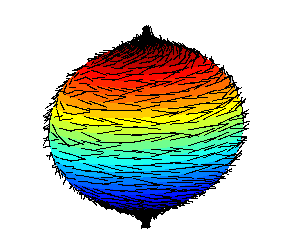
"Hairy ball theorem"
says no
Without singularities
or discontinuities?
Light Field Networks
V. Sitzmann, S. Rezchikov, W.T. Freeman, J.B. Tenenbaum, F. Durand, Light field networks: Neural scene representations with single-evaluation rendering, in: ArXiv, 2021.
- Represents rays using Plücker coordinates

Light Field Networks
V. Sitzmann, S. Rezchikov, W.T. Freeman, J.B. Tenenbaum, F. Durand, Light field networks: Neural scene representations with single-evaluation rendering, in: ArXiv, 2021.
- Represents rays using Plücker coordinates

Light Field Networks
V. Sitzmann, S. Rezchikov, W.T. Freeman, J.B. Tenenbaum, F. Durand, Light field networks: Neural scene representations with single-evaluation rendering, in: ArXiv, 2021.
- Represents rays using Plücker coordinates

Light Field Networks
V. Sitzmann, S. Rezchikov, W.T. Freeman, J.B. Tenenbaum, F. Durand, Light field networks: Neural scene representations with single-evaluation rendering, in: ArXiv, 2021.
- Represents rays using Plücker coordinates

4 DoF!
Light Field Networks
V. Sitzmann, S. Rezchikov, W.T. Freeman, J.B. Tenenbaum, F. Durand, Light field networks: Neural scene representations with single-evaluation rendering, in: ArXiv, 2021.
- Represents rays using Plücker coordinates
- From ray predict color
- Fast
- Simple shading only
- Geometry?
Light Field Networks
V. Sitzmann, S. Rezchikov, W.T. Freeman, J.B. Tenenbaum, F. Durand, Light field networks: Neural scene representations with single-evaluation rendering, in: ArXiv, 2021.

- Compute depth maps by analyzing epipolar images
- Expensive \((O(n^3))\)
- Sparse
- \(\Rightarrow\) Cannot disentangle materials and illumination
Light Field Networks
V. Sitzmann, S. Rezchikov, W.T. Freeman, J.B. Tenenbaum, F. Durand, Light field networks: Neural scene representations with single-evaluation rendering, in: ArXiv, 2021.
Light Field Networks
V. Sitzmann, S. Rezchikov, W.T. Freeman, J.B. Tenenbaum, F. Durand, Light field networks: Neural scene representations with single-evaluation rendering, in: ArXiv, 2021.
Primary Ray Intersection Fields
B.Y. Feng, Y. Zhang, D. Tang, R. Du, A. Varshney, PRIF: Primary Ray-Based Implicit Function, in: S. Avidan, G. Brostow, M. Cissé, G.M. Farinella, T. Hassner (Eds.), Computer Vision – ECCV 2022, Springer Nature Switzerland, Cham, 2022: pp. 138–155. https://doi.org/10.1007/978-3-031-20062-5_9.
Primary Ray Intersection Fields
B.Y. Feng, Y. Zhang, D. Tang, R. Du, A. Varshney, PRIF: Primary Ray-Based Implicit Function, in: S. Avidan, G. Brostow, M. Cissé, G.M. Farinella, T. Hassner (Eds.), Computer Vision – ECCV 2022, Springer Nature Switzerland, Cham, 2022: pp. 138–155. https://doi.org/10.1007/978-3-031-20062-5_9.
Primary Ray Intersection Fields


Fit surface
B.Y. Feng, Y. Zhang, D. Tang, R. Du, A. Varshney, PRIF: Primary Ray-Based Implicit Function, in: S. Avidan, G. Brostow, M. Cissé, G.M. Farinella, T. Hassner (Eds.), Computer Vision – ECCV 2022, Springer Nature Switzerland, Cham, 2022: pp. 138–155. https://doi.org/10.1007/978-3-031-20062-5_9.
MARFs
By pbsds
MARFs
- 291



