Book 2. Credit Risk

FRM Part 2

CR 13. Credit Derivatives

Presented by: Sudhanshu

Module 1. Credit Default Swaps

Module 2. CDS Extensions and Credit Indices

Module 3. Total Return Swaps and Collateralized Debt Obligations

Module 1. Credit Default Swaps

Topic 1. Credit Derivative Products

Topic 2. Credit Default Swap Structure

Topic 3. CDS Valuation

Topic 1. Credit Derivative Products

Credit derivatives are financial instruments used to transfer credit risk from one party to another without transferring the underlying asset. They allow investors to manage exposure to potential defaults, changes in credit ratings, or other credit events. The primary purpose of these products is to provide an alternative way for banks and other financial institutions to diversify and reduce their credit risk exposure, which is a major component of their business.
Types of Credit Derivatives
- Credit Default Swaps (CDS): The most common type of credit derivative. A CDS is a bilateral contract where one party (the protection buyer) pays a periodic fee to another party (the protection seller) in exchange for a payoff if a specified credit event occurs for a reference entity.
- Credit Default Swaptions: An option to enter into a CDS at a future date at a specified strike price.
- Total Return Swaps (TRS): A swap where the total return of an underlying asset (including interest, dividends, and appreciation/depreciation) is exchanged for a fixed or floating rate payment. This allows a party to gain economic exposure to an asset without owning it.
- Credit-Linked Notes (CLNs): A hybrid security that combines a bond with a CDS. The investor receives a coupon but the principal repayment is contingent on the credit performance of a reference entity. If a credit event occurs, the investor's principal may be reduced or eliminated.

Topic 2. Credit Default Swap (CDS) Structure

A CDS is essentially a form of insurance against a default. It's an over-the-counter (OTC) contract between two parties: the protection buyer and the protection seller. The contract specifies a reference entity (the debtor, e.g., a corporation or sovereign nation) and a credit event (e.g., bankruptcy, failure to pay, or restructuring).
Key Components of a CDS
- Protection Buyer: The party who pays a periodic premium (the CDS spread) and receives protection. This is often an investor who owns the underlying bond or wants to hedge against a potential default.
- Protection Seller: The party who receives the premium and agrees to make a payment to the protection buyer if a credit event occurs. This party is essentially taking on the credit risk in exchange for the premium.
- Reference Entity: The company or country on which the CDS is written.
- Notional Principal: The face value of the underlying asset being protected. The credit event payout is based on this amount.
- CDS Spread: The annual premium paid by the protection buyer to the protection seller. It is typically quoted in basis points (bps) of the notional principal. A higher spread indicates a higher perceived risk of default.
- Credit Event: The trigger that initiates the payout from the protection seller to the protection buyer.

The protection buyer makes regular payments (quarterly, for example) to the protection seller. If a credit event does not occur by the maturity of the contract, the protection seller keeps all the premiums and the contract expires. If a credit event does occur, the protection seller must compensate the protection buyer. This can be done in one of two ways:
- Physical Settlement: The protection buyer delivers the defaulted bonds (or other deliverable obligations) to the protection seller, who in turn pays the full notional value of the bonds.
- Cash Settlement: The protection seller pays the protection buyer the difference between the notional value and the recovery value of the defaulted bonds. The recovery value is determined by a credit auction process.

Topic 2. Credit Default Swap (CDS) Structure

Practice Questions: Q1

Q1. Modus Corp's 7 -year, 5 % coupon bond is rated AA. The annual CDS spread on a 7 -year bond is 3 %. The swap spread is flat at 25 bps, while the swap fixed rate is 3 % for 5 years and 4 % for 7 years. To prevent arbitrage, Modus Corp's bond should most likely yield:

A. 7.00 %.

B. 7.25 %.

C. 7.75 %.

D. 8.00 %.

Practice Questions: Q1 Answer

Explanation: A is correct.

Arbitrage-free conditions indicate that:
CDS-bond basis = CDS spread – bond yield spread = 0
Thus, CDS spread = bond yield spread = 3% (given).
Bond yield spread = bond yield – swap fixed rate
3% = bond yield – 4% (make sure to use the 7-year swap fixed rate)
Therefore, the bond yield = 7%.

Topic 3. CDS Valuation

Valuing a CDS involves calculating the present value of the expected future cash flows for both the protection buyer and the protection seller. The valuation is based on the no-arbitrage principle, meaning the present value of the payments must equal the present value of the expected payouts.
The Two Legs of a CDS
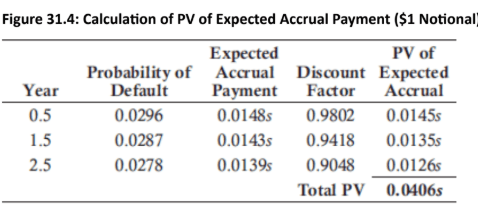
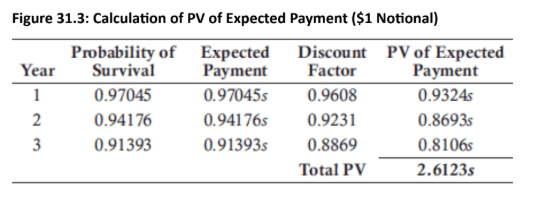
- Premium Leg: The stream of payments made by the protection buyer to the protection seller. The value of this leg is the sum of the discounted expected premium payments. The probability of the reference entity surviving (not defaulting) is a key factor in this calculation.
- where $r_{t}$ is the risk-free rate, $p_{t}$ is the cumulative default probability, and $t$ is the time period.
- Protection Leg: The single payment made by the protection seller to the protection buyer in the event of a default. The value of this leg is the discounted expected payout. This expectation is a function of the probability of default and the loss given default (LGD), which is the percentage of the notional value that is lost if a default occurs.

\text { Value}_{\text {Premium Leg }}=\sum_{t=1}^N e^{-r_t t} \times\left(1-p_t\right) \times \text { Premium Payment}_t

\text { Value}_{\text {Protection Leg }}=\sum_{t=1}^N e^{-r_t t} \times(\text { Loss Given Default }) \times(\text { Probability of Default at } t)

The loss given default is typically calculated as $1 - Recovery Rate$ .
The Fair CDS Spread: The fair CDS spread is the rate at which the present value of the premium leg equals the present value of the protection leg. This is the no-arbitrage spread that would make the contract's initial value zero.
The primary inputs for this valuation are:
- Default Probabilities: Derived from credit ratings, bond spreads, or market-implied data.
- Recovery Rate: The expected value recovered by bondholders in case of default.
- Risk-Free Interest Rate Curve: Used to discount future cash flows.
- The value of the CDS to either party at any time after issuance is the difference between the current market spread and the original contracted spread, discounted by the probability of default.

\text { Value}_{\text {Premium Leg }}=\text { Value}_{\text {Protection Leg }}

Topic 3. CDS Valuation

Practice Questions: Q2

Q2. Xeta Corp's hazard rate is estimated to be 2 % over the next five years. The probability of default in Year 2 for Xeta is closest to:

A. 1.94 %.

B. 1.98 %.

C. 2.00 %.

D. 2.23 %.

Practice Questions: Q2 Answer

Explanation: A is correct.

The probability of survival in Years 1 and2

and

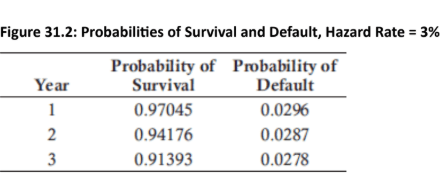
The probability of default in Year 2 = 0.9802 – 0.9608 = 0.0194, or 1.94%.

e^{-0.02 \times 1}=0.9802

e^{-0.02 \times 2}=0.9608

Practice Questions: Q3

Q3. CDS spreads are calculated such that the PV of:

A. accrual payments is zero.

B. expected payoff is less than the PV of expected payments during the life of the CDS.

C. expected payoff is equal to the PV of expected payments during the life of the CDS.

D. expected payoff is greater than the PV of expected payments during the life of the CDS.

Practice Questions: Q3 Answer

Explanation: C is correct.

The CDS spread is set such that the PV of expected payoff is equal to the PV of
expected payments during the life of the swap. The PV of expected payments
includes the PV of expected periodic swap spread payments plus the PV of
expected accrual payments.

Module 2. CDS Extensions and Credit Indices

Topic 1. Default Probabilities Used to Value a CDS

Topic 2. Marking a CDS to Market

Topic 3. Binary CDS

Topic 4. Credit Indices

Topic 5. Fixed Coupons

Topic 6. CDS Forwards and Options

Topic 1. Default Probabilities Used to Value a CDS

Risk-Neutral vs. Actual Default Probabilities: The probability of default (PD) used to value a CDS is not the true or "actual" PD. Instead, it's the risk-neutral (RN) probability of default, which is the probability implied by the CDS spread quoted in the market.
Calculating Probabilities from Hazard Rates: The risk-neutral PD is calculated from the hazard rate ( $λ$ ), which is the default intensity. The probability of survival (PS) at time $t$ is calculated as $P S_{t} = e^{- λ \times t}$ . The probability of default (PD) in year $t$ is then the difference between the probability of survival in the previous year and the current year: $P D_{t} = (P S_{t - 1} - P S_{t})$ .
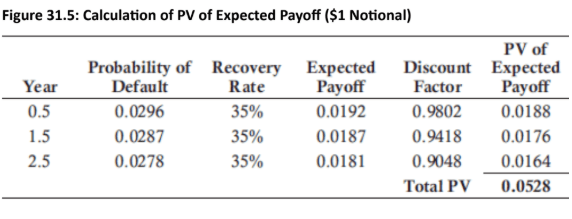
Example Calculation: For a 3-year CDS with a 3% hazard rate, the probability of survival for Year 1 is $e^{- 1 \times 0.03} = 0.97045$ . The PD in Year 1 is $1 - 0.97045 = 0.0296$ .
Relationship with Recovery Rate: The risk-neutral PD is approximately proportional to $1/ (1 - Recovery Rate)$ . If you assume a higher recovery rate, the risk-neutral probability of default will also be high, which keeps the actual market CDS spread constant.

Topic 2. Marking a CDS to Market

Daily Valuation: CDS contracts are marked to market (MtM) daily to determine their current value. The MtM value to the protection seller is the difference between the present value (PV) of expected payments and the PV of the expected payoff.
- $MtM value to protection seller = PV of expected payments PV of expected payoff$
Impact of Spread Changes:
- If the CDS spread narrows (decreases), the protection buyer loses value, while the protection seller gains an equal amount.
- If the CDS spread widens (increases), the protection buyer gains value, while the protection seller loses an equal amount.
Example: A 3.5-year swap initiated at a 1.50% spread has three years remaining, and the spread has widened to 1.99%. With a notional principal of $1 million, the PV of expected payments is

$$39, 800$ ( $2.6529 \times 0.015 \times $1, 000, 000$ ). The PV of the expected payoff is $$52, 800$ ( $0.0528 \times $1, 000, 000$ ). The MtM value for the protection seller is a loss of $$13, 000$ ( $0.0398 - 0.0528 = - 0.013$ per $$1$ notional). The protection buyer gains $$13, 000$ .

Topic 3. Binary CDS

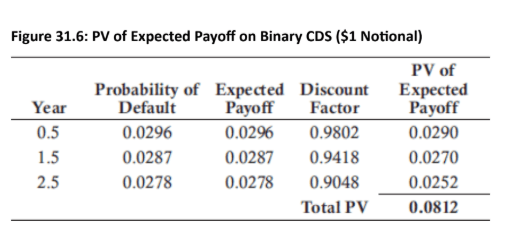
Fixed Payout: A binary CDS differs from a standard CDS because its payoff on default is a fixed, full notional amount, irrespective of the recovery rate.
Valuation: The calculations for a binary CDS are simpler because the recovery rate is assumed to be 0%.
- The expected payoff is simply the probability of default (PD) multiplied by the notional principal, since the recovery rate is assumed to be zero.
Spread Calculation: The spread for a binary CDS can be calculated by dividing the spread of a standard (vanilla) CDS by $(1 - Recovery Rate)$ . Using the example from the PDF, with a vanilla spread of 1.99% and a 35% recovery rate, the binary CDS spread would be $1.99/ (1 - 0.35) = 3.06%$ .
Higher Cost: As expected, the price to purchase protection in a binary CDS is higher because it assumes a 0% recovery rate, which is riskier for the protection seller.

Practice Questions: Q1

Q1. Banko, Inc., entered into a $5 million notional, 5-year CDS as a protection buyer two years ago at a spread of 1.85%. The current 3-year CDS spread for the same reference entity is 2.30% based on the PV of expected payoff of 0.0312 per $1 notional. The value of the CDS to Banko, Inc., is closest to:

A. -$ 45,000.

B. -$ 30,900.

C. +$ 30,500.

D. +$ 53,000.

Practice Questions: Q1 Answer

Explanation: C is correct.

Recognize that the value of the CDS is calculated such that:
current PV of expected payments = current PV of expected payoff = 0.0312
Using the current spread of 2.30%, the current PV of expected payments = 0.023 ×s.
s = 0.0312/0.023 = 1.3565
Applying this value to the initial CDS spread of 1.85% yields:
PV of expected payments (based on 1.85%) = 0.0185 × 1.3565 = 0.0251
Value to the protection buyer = PV of expected payoff − PV of expected payments
= 0.0312 – 0.0251 = 0.0061 per $1 notional
The swap value for the $5 million notional = 0.0061 × 5,000,000 = $30,500.
Because the spread has widened, the protection buyer gains.

Topic 4. Credit Indices

Diversified Exposure: Credit indices, such as CDX NA IG (North American) and iTraxx Europe (European), allow investors to gain exposure to the credit risk of multiple companies simultaneously.
Structure: CDX NA IG and iTraxx Europe each have an equally-weighted exposure to 125 investment-grade companies. The notional principal of the index is the sum of the notional principals for all underlying CDS contracts.
Mechanism: If a company in the index defaults, the protection seller makes a payoff based on $(1 - Recovery Rate)$ on the defaulting company's notional principal. The contract continues with the remaining companies, and the annual payment is adjusted accordingly.
Updating: The indices are updated twice a year for new contracts, with companies whose ratings fall below investment grade being replaced.

Practice Questions: Q2

Q2. If one of the entities in the CDX NA IG index defaults, the CDS index would most likely:

A. make a payoff and be discontinued.

B. continue with a replacement entity, with no change to the notional principal.

C. continue with 99 entities, and the notional principal of each entity would be reduced by 1 %.

D. continue with 124 entities, and the notional principal of each entity would remain the same.

Practice Questions: Q2 Answer

Explanation: D is correct.

The CDX NA IG index has 125 equally-weighted entities. When one of these
entities defaults, the existing CDS would continue with 124 entities with the same notional per entity.

Topic 5. Fixed Coupons

Standardization: To improve liquidity and standardize the CDS market, contracts are now traded with a fixed coupon rate rather than a negotiated spread.
Upfront Premium: To compensate for the difference between the fixed coupon rate and the actual market CDS spread, a one-time upfront premium is paid.
Calculation: The upfront premium percentage is calculated using the formula: $D \times (s - c)$ .
- $D$ = CDS payment duration
- $s$ = CDS spread
- $c$ = coupon rate
Payment Direction:
- If the market spread ( $s$ ) is higher than the fixed coupon ( $c$ ), the protection buyer makes an upfront payment to the protection seller.
- If the market spread ( $s$ ) is lower than the fixed coupon ( $c$ ), the protection seller makes an upfront payment to the protection buyer. The price of the contract will be greater than 100.

Topic 6. CDS Forwards and Options

CDS Forwards: A CDS forward is a contract that allows a party to agree to enter into a standard CDS at a specified future date and at a predetermined fixed spread. The contract ceases to exist if the reference entity defaults before the start date.
CDS Options (Swaptions): A CDS option gives the holder the right, but not the obligation, to enter into a CDS at a specified future date and strike spread in exchange for a premium.
- An option to buy protection is a call option and would be exercised if the CDS spread is higher than the strike spread.
- Just like forwards, if the reference entity defaults before the option's maturity, the option ceases to exist.
Premium Payment: CDS options require a premium payment, while CDS forwards entered at market rates do not.

Practice Questions: Q3

Q3. Which of the following statements about CDS forwards and CDS options is most accurate?

A. CDS forwards entered at market rates require a premium payment, while CDS options do not.

B. CDS options entered at market rates require a premium payment, while CDS forwards do not.

C. Both CDS forwards entered at market rates as well as CDS options require a premium payment.

D. Neither CDS forwards entered at market rates nor CDS options require a premium payment.

Practice Questions: Q3 Answer

Explanation: B is correct.

CDS forwards entered at market rates do not require a premium payment.
However, CDS options do require a premium payment to the option writer who is willing to take the risk of option exercise.

Module 3. Total Return Swaps and Collateralized Debt Obligations

Topic 1. Total Return Swap

Topic 2. Collateralized debt obligations

Topic 3. Synthetic CDOs

Topic 4. Synthetic CDO Valuation

Topic 5. Gaussian Copula Approach

Topic 6. Implied Correlation

Topic 7. Gaussian Copula Model Alternatives

Topic 1. Total Return Swap

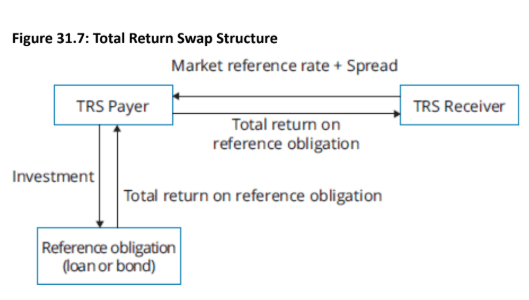
What it is: A total return swap (TRS) is a contract where one party (the total return receiver) receives the total return of a specified reference asset (e.g., a bond or loan) and, in exchange, pays a floating interest rate (e.g., LIBOR plus a spread) to the other party (the total return payer).
Total Return: The total return includes all interest or dividend payments, as well as any appreciation in the asset's value. If the asset's value depreciates, the receiver must pay the loss to the payer.
Purpose: The main benefit is that the receiver gains economic exposure to the asset without actually owning it, which can be useful for avoiding balance-sheet implications or shorting an asset. The payer, who owns the asset, can hedge the risk of its value decreasing while still earning a stable cash flow.
Key Distinction: Unlike a credit default swap (CDS), a TRS transfers both the credit risk and the market risk (interest rate and price risk) of the underlying asset.

Topic 2. Collateralized Debt Obligations

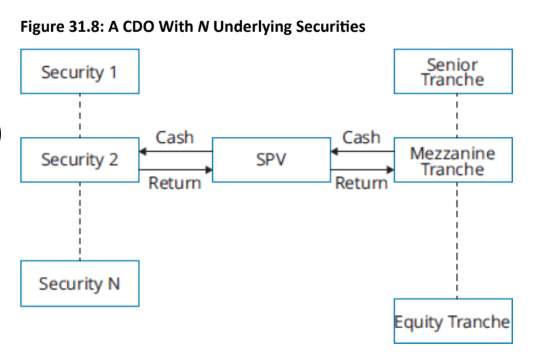
What they are: A Collateralized Debt Obligation (CDO) is a structured financial product that pools together a portfolio of risky debt securities, such as corporate bonds or loans.
Tranching: The CDO issues different classes of claims against this portfolio, known as tranches. These tranches have different levels of risk and seniority.
- Equity Tranche: The lowest-rated and riskiest tranche, which absorbs the first losses from the portfolio. It receives the leftover cash flows and is unrated.
- Mezzanine Tranches: These are in the middle, with a moderate level of risk and a higher rating than the equity tranche.
- Senior Tranche: This is the highest-rated and safest tranche, which receives cash flows and principal repayments first. It bears the lowest risk of default.
Cash Flow Distribution: A waterfall is a rule-based system that dictates how the cash flow from the underlying securities is distributed to the different tranches, with the most senior tranche being paid first.

Topic 2. Collateralized Debt Obligations

Topic 3. Synthetic CDOs

How they differ: A synthetic CDO provides credit risk exposure similar to a traditional (or "cash") CDO, but it is created using credit default swaps (CDS) rather than by purchasing actual debt securities.
Mechanism: An originator sells credit protection on a portfolio of reference entities by entering into multiple CDS contracts. The originator then "slices" the risk of this portfolio of CDS into tranches and sells these tranches to investors.
No Asset Ownership: A key characteristic is that no underlying bonds or loans are bought or sold. The investors (protection sellers) effectively gain exposure to credit risk without having to purchase the specified bonds, receiving CDS spreads in return. The originator pays out any default losses.

Topic 4. Synthetic CDO Valuation

Challenge: The primary challenge in valuing a synthetic CDO is determining the default correlation between the underlying assets. It's not enough to just know the individual default probabilities; you also need to know the likelihood of multiple entities defaulting at the same time.
The Approach: The common valuation method is the Gaussian copula model of time to default. This model prices the different tranches based on the likelihood of a certain number of defaults occurring within the portfolio.
Model Inputs: The model requires three key inputs:
1. The notional principal of each underlying CDS.
2. The risk-free yield curve for discounting cash flows.
3. The hazard rates (default probabilities) of each underlying reference entity.

Topic 5. Gaussian Copula Approach

Simplified Default: The Gaussian copula model simplifies the valuation problem by assuming that the time to default for each company is driven by a single common factor (e.g., the state of the economy) and an idiosyncratic factor unique to each company.
The Framework: The model uses a latent variable model. The default time for each company is triggered when a normally distributed latent variable ( $Y_{i}$ ) falls below a certain threshold. The variables are modeled as:
- $M$ : The single common, normally distributed factor (the "market factor").
- $Z_{i}$ : The normally distributed idiosyncratic factor for each company $i$ .
- $ρ$ : The correlation coefficient, which represents the correlation between the companies' defaults.
Valuation: The value of each tranche can then be calculated as the present value of the expected loss for that tranche, using the assumed correlation and default probabilities. The model links the probability of multiple defaults to the assumed correlation.

Y_i=\sqrt{\rho}M+\sqrt{1-\rho}Z_i

Practice Questions: Q1

Q1. At inception, the tranches in a synthetic CDO are priced to earn a spread that is:

A. equal for each tranche.

B. consistent with their seniority.

C. aggregate in amount to the premium paid to binary CDSs.

D. higher for senior tranches, as they represent a larger notional principal.

Practice Questions: Q1 Answer

Explanation: B is correct.

At inception, the tranches in a synthetic CDO are priced to earn a spread that is
consistent with their risk level (i.e., seniority in the distribution waterfall). The
aggregate spread amount is set equal to the premium received as a protection
seller in a vanilla CDS. While senior tranches normally have a higher notional
principal, the spread (as a rate) is lower due to the lower credit risk of the senior
tranches.

Topic 6. Implied Correlation

Model Deficiency: A key criticism of the Gaussian copula model is that a single correlation parameter ( $ρ$ ) cannot accurately price all the tranches of a CDO simultaneously. The market often quotes different prices for different tranches, which, when reverse-engineered using the model, yield different correlation values.
What it is: The implied correlation is the correlation that, when used in the Gaussian copula model, produces a theoretical price that matches the actual market price of a specific tranche.
The Correlation Smile: The observed phenomenon of different tranches having different implied correlations is known as the implied correlation smile or skew. Typically, junior (equity) tranches have a much higher implied correlation than senior tranches. This indicates that the market expects a higher chance of multiple defaults than what the model would predict with a single correlation parameter.

Practice Questions: Q2

Q2. Base correlation and compound correlation are both:

A. tranche correlations.

B. implied correlations.

C. not relevant for synthetic CDOs.

D. exhibiting a skew with correlations rising with tranche seniority.

Practice Questions: Q2 Answer

Explanation: B is correct.

Compound (or tranche) correlation and base correlation are implied correlations
that are calculated differently. While compound correlations exhibit a smile
pattern, base correlations show a skew pattern.

Topic 7. Gaussian Copula Model Alternatives

The Need for Alternatives: The failure of the Gaussian copula model during the 2008 financial crisis, particularly its inability to capture the "fat-tail" risk of multiple defaults, led to the development of alternative models.
T-Copula: One alternative is the Student's t-copula, which is similar to the Gaussian copula but uses a t-distribution instead of a normal distribution. The t-distribution has "fatter tails," meaning it assigns a higher probability to extreme events (like a large number of defaults occurring simultaneously), which better reflects market reality.
Stochastic Correlation Models: Another approach is to use models where the correlation parameter is not a constant but a random variable. These stochastic correlation models allow for dynamic changes in correlation over time, better capturing market panic and changes in risk appetite.
Jump-to-Default Models: These models explicitly account for the possibility of a sudden, unexpected jump in the number of defaults, which is not well-captured by the smooth, continuous process of the Gaussian copula. These models are often used to price options on credit indices.

Practice Questions: Q3

Q3. The structural model of credit risk is most likely a(n):

A. dynamic model.

B. heterogenous model.

C. implied copula model.

D. random recovery rate model.

Practice Questions: Q3 Answer

Explanation: A is correct.

Dynamic models, including structural and reduced-form models, capture the
evolution of loss on a collateral pool over time. Heterogenous models allow for
speciication of different distributions for time to default for different reference
entities included in the collateral pool. Random recovery rates and factor loadings

are based on the negative relationship between default rates and recovery rates.
The implied copula model is derived from market prices.

CR 13. Credit Derivatives

By Prateek Yadav

Book 2. Credit Risk

FRM Part 2

CR 13. Credit Derivatives

Presented by: Sudhanshu

Module 1. Credit Default Swaps

Module 2. CDS Extensions and Credit Indices

Module 3. Total Return Swaps and Collateralized Debt Obligations

Module 1. Credit Default Swaps

Topic 1. Credit Derivative Products

Topic 2. Credit Default Swap (CDS) Structure

Topic 2. Credit Default Swap (CDS) Structure

Practice Questions: Q1

Practice Questions: Q1 Answer

Topic 3. CDS Valuation

Topic 3. CDS Valuation

Topic 3. CDS Valuation

Practice Questions: Q2

Practice Questions: Q2 Answer

Practice Questions: Q3

Practice Questions: Q3 Answer

Module 2. CDS Extensions and Credit Indices

Topic 1. Default Probabilities Used to Value a CDS

Topic 2. Marking a CDS to Market

Topic 3. Binary CDS

Practice Questions: Q1

Practice Questions: Q1 Answer

Topic 4. Credit Indices

Practice Questions: Q2

Practice Questions: Q2 Answer

Topic 5. Fixed Coupons

Topic 6. CDS Forwards and Options

Practice Questions: Q3

Practice Questions: Q3 Answer

Module 3. Total Return Swaps and Collateralized Debt Obligations

Topic 1. Total Return Swap

Topic 2. Collateralized Debt Obligations

Topic 2. Collateralized Debt Obligations

Topic 3. Synthetic CDOs

Topic 4. Synthetic CDO Valuation

Topic 5. Gaussian Copula Approach

Practice Questions: Q1

Practice Questions: Q1 Answer

Topic 6. Implied Correlation

Practice Questions: Q2

Practice Questions: Q2 Answer

Topic 7. Gaussian Copula Model Alternatives

Practice Questions: Q3

Practice Questions: Q3 Answer

CR 13. Credit Derivatives

More from Prateek Yadav