Book 2. Credit Risk
FRM Part 2
CR 9. Estimating Default Probabilities

Presented by: Sudhanshu
Module 1. Credit Ratings and Default Probabilities
Module 2. Credit Default Swaps
Module 3. Comparing Default Probabilities
Module 1. Credit Ratings and Default Probabilities

Topic 1. Compare Agencies’ Ratings to Internal Credit Rating Systems
Topic 2. Altman's Z-Score
Topic 3. Historical Default Probabilities
Topic 4. Borrowing Rating vs. Probability of Default
Topic 5. Hazard Rates
Topic 6. Recovery Rates





Topic 1. Compare Agencies’ Ratings to Internal Credit Rating Systems
-
Overview of Credit Ratings External Rating Agencies: Major agencies like S&P provide credit ratings for large, publicly traded bond issuers. These ratings reflect an issuer's credit quality and are meant to be stable, taking a long-term view that "ratings through an economic cycle" is important. They avoid frequent changes based on short-term information.
-
Internal Credit Rating Systems: These are developed by lenders for small- and mid-sized firms that typically aren't rated by external agencies.
Key Differences: Scope: External agencies focus on large, public companies. Internal systems are used for smaller, private firms.
-
Approach: Internal systems often use financial statement analysis, focusing on profitability (e.g., return on equity), liquidity (e.g., quick ratio), and solvency (e.g., debt-to-equity ratio) to determine a firm's repayment ability.
-
-
Topic 2. Altman's Z-score
-
Altman's Z-score is a specific application of Linear Discriminant Analysis (LDA), a statistical method used for creating credit scoring models.
-
Purpose: It's used to predict the likelihood of a firm defaulting. The model was initially developed for publicly traded manufacturing firms but has been adapted for private ones as well.
-
The Formula: Z=1.2X1+1.4X2+3.3X3+0.6X4+0.999X5.
-
The variables (X1 to X5) are a set of five key financial ratios.
-
-
-
Interpreting the Z-Score: The Z-score classifies a firm's credit quality based on a set of guidelines.
-
Z-Score > 3: No default is likely.
-
2.7 - 3: Potential default.
-
1.8 - 2.7: Reasonable probability of default.
-
< 1.8: High likelihood of default.
-
Conclusion: A higher Z-score indicates a higher probability of being solvent, while a lower score suggests a higher risk of insolvency.
-
Practice Questions: Q1
Q1. The following financial data pertains to Nielsen Corp. (Nielsen):
The Altman’s Z-score equation is as follows:
When using the computed Z-score to classify Nielsen based on credit quality, what is the most appropriate classification for the company?
A. No default is likely.
B. Potential default.
C. Reasonable probability of default.
D. High likelihood of default.

Practice Questions: Q1 Answer
Explanation: C is correct.
The five financial ratios for computing Altman’s Z-score are as follows:
1. X1: working capital / total assets = 525,000 / 5,100,000
2. X2: retained earnings / total assets = 1,120,000 / 5,100,000
3. X3: earnings before interest and taxes (EBIT) / total assets = 480,000 /5,100,000
4. X4: market value of equity / book value of total liabilities = 4,215,000 /1,850,000
5. X5: sales / total assets = 1,760,000 / 5,100,000
Altman’s Z-score is then as follows:
Z = 1.2 × (525,000 / 5,100,000) + 1.4 × (1,120,000 / 5,100,000) + 3.3 × (480,000 / 5,100,000) + 0.6 × (4,215,000 / 1,850,000) + 0.999 × (1,760,000 / 5,100,000)
= 0.1235 + 0.3075 + 0.3106 + 1.3670 + 0.3448 = 2.4534
The following guidelines apply for assessing credit quality:
> 3: no default is likely
2.7-3: potential default
1.8-2.7: reasonable probability of default
< 1.8: high likelihood of default
Therefore, with a Z-score of 2.4534, Nielsen has a reasonable probability of
default.
Topic 3. Historical Default Probabilities
-
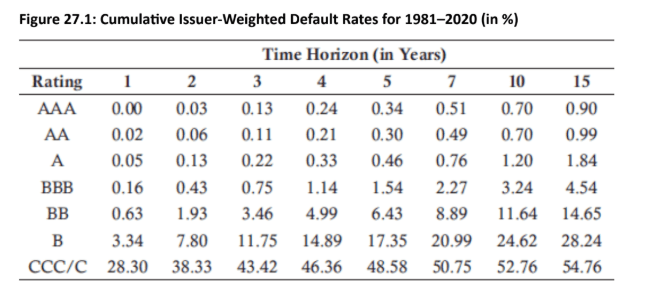
A rating migration matrix, like the one from S&P, quantifies the average default rates of issuers based on their initial credit rating.
-
Rating Scale: Ratings range from AAA (highest quality) to D (default). Investment-grade bonds are rated AAA to BBB, while non-investment-grade ("junk") bonds are BB to D.
-
Example (S&P Data): A bond with an AA rating has a 0.02% chance of defaulting by the end of Year 1 and a 0.06% chance by the end of Year 2. These are cumulative probabilities of default.
-
- Calculating Default Probabilities: Cumulative Probability of Default: The probability that a firm will default by a certain time. For an AA-rated bond, the cumulative probability of default by the end of Year 3 is 0.11%
-
Marginal Probability of Default: The probability that a default will occur within a specific year, given that it hasn't defaulted before that year.
-
Example (AA-rated bond): The marginal probability of defaulting in Year 3 is the cumulative probability at the end of Year 3 minus the cumulative probability at the end of Year 2.
-
0.11%−0.06%=0.05%.
-
-
Unconditional Default Probability: The same as the marginal probability of default.
-
Example (BB-rated bond): The unconditional default probability in Year 4 is the difference between the cumulative probabilities at the end of Year 4 and Year 3.
-
4.99%−3.46%=1.53%.
-
Topic 3. Historical Default Probabilities
Practice Questions: Q2
Q2. The following information is an excerpt from a rating migration matrix for a B-rated bond:
What is the probability that the bond will default during the fourth year conditional on no earlier default?
A. 2.46%.
B. 2.79%.
C. 3.14%.
D. 3.56%.
Practice Questions: Q2 Answer
Explanation: D is correct.
The probability of a B-rated bond defaulting in the fourth year is 14.89% - 11.75%= 3.14%.
The probability that the bond will survive until the end of the third year is 100%- 11.75% = 88.25%.
Thus, the probability that the bond will default during the fourth year conditional on no earlier default is computed as 3.14% / 88.25% = 3.56%.
Topic 4. Borrowing Rating vs. Probability of Default
-
The Relationship: General Rule: A lower borrowing rating generally corresponds to a higher probability of default, and a higher rating corresponds to a lower probability of default.
-
Time and Default Probability: The relationship between time and the marginal probability of default can vary depending on the rating.
-
Investment-Grade Bonds: For these and some non-investment-grade bonds, the marginal probability of default tends to increase with time in the initial years. This is based on the assumption that while an issuer starts stable, its financial condition could deteriorate over time. For an AA-rated bond, the marginal default probabilities for Years 1, 2, and 3 are 0.02%, 0.04%, and 0.05%, respectively.
-
Non-Investment-Grade Bonds: For some of these bonds, the marginal probability of default may decrease over time after the initial years. The idea is that if the issuer has survived the critical initial years, its financial state might not be as risky as first thought. For a B-rated bond, the marginal default probabilities for Years 1, 2, 3, and 4 are 3.34%, 4.46%, 3.95%, and 3.24%.
-
-
Topic 5. Hazard Rates
- Hazard Rate: The hazard rate is also called the conditional default probability. It is the probability of default within a specific period, conditional on no earlier default.
-
Calculation: Conditional default probability = (Unconditional default probability) / (Probability of no earlier default).
-
Example: For a BB-rated bond in Year 4, the unconditional default probability is 1.53%. The probability of no earlier default (by the end of Year 3) is 100% - 3.46% = 96.54%.
-
The conditional default probability (hazard rate) is
1.53%/96.54%=1.58%.
-
Formula: The probability of default by time t can be approximated with the average hazard rate (λ(t)):
-
-
-
- Hazard Rates and Credit Spreads: Hazard rates can be approximated using credit spreads, such as CDS spreads or bond yield spreads.
-
Formula: For a bond trading near its par value, the average hazard rate is:
Where s(T) is the credit spread for maturity T, and RR is the recovery rate.
Example: If a 5-year credit spread is 210 basis points (2.1%) and the recovery rate is 30%, the average annual conditional probability of default is 0.021/(1−0.3)=3%.
Topic 5. Hazard Rates
Topic 6. Recovery Rates
-
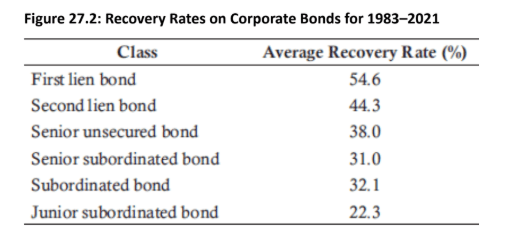
Defining Recovery Rates : A recovery rate is the percentage of the face value of a debt that creditors are likely to recover in the event of a default or bankruptcy.
-
Seniority: The recovery rate is highly dependent on the seniority of the bond.
-
More senior bonds (e.g., first lien bonds) have higher average recovery rates (e.g., 54.6%).
-
More junior bonds (e.g., subordinated bonds) have lower average recovery rates (e.g., 32.1%).
-
-
-
Recovery Rates and Default Rates Inverse Relationship: Recovery rates are negatively correlated with default rates. This means when one is high, the other is low.
-
Strong Economy: In a strong economy, there are few defaults, and the average recovery rate is relatively high.
-
Weak Economy: In a weak economy, there are more defaults, and the average recovery rate is relatively low.
-
Lender Challenge: This inverse relationship poses a significant challenge for lenders during a weak economy, as they face both high default rates and low recovery rates.
-
-
Example (Mortgages): Higher mortgage default rates lead to more foreclosures and a surplus of properties on the market, which in turn drives down property prices and reduces the lender's recovery rate.
Topic 6. Recovery Rates
Module 2. Credit Default Swaps

Topic 1. Credit Default Swap and its Mechanics
Topic 2. Credit Indices
Topic 3. Fixed Coupons
Topic 4. CDS Spreads
Topic 5. CDS-Bond Basis
Topic 6. Approximating Hazard Rates
Topic 7. Most Precise Hazard Rates






Topic 1. Credit Default Swap and its Mechanics
- A credit default swap (CDS) is a credit derivative where one party makes payments to another for credit protection. The default protection buyer makes regular, usually quarterly, payments to the default protection seller. In return, the seller agrees to pay the buyer a pre-specified amount if a credit event occurs. Credit events can include non-timely payment, debt restructuring, or bankruptcy.
-
Mechanics
-
Underlying Entity: The CDS is based on a specific company, or "reference entity".
-
Settlement: If a credit event occurs, the swap can be settled in two ways:
-
Physical Delivery: The seller pays the buyer the notional principal of the bonds and receives the defaulted bonds in exchange. The contract often specifies a list of acceptable bonds that can be delivered.
-
Cash Settlement: Dealers are surveyed to determine the mid-point between bid and ask prices of the cheapest-to-deliver (CTD) bond. The cash payoff is then the difference between the face value and the market value of the bond. For example, if a CTD bond is valued at $0.40 to the dollar, the cash payoff is 60% of the notional principal.
-
Payments: The protection buyer's premium payments cease after a credit event.
-
-

Topic 2. Credit Indices
-
Credit indices are portfolios of CDSs that allow investors to trade credit risk on a broad basket of reference entities. Two well-known investment-grade credit indices are CDX NA IG (North America) and iTraxx Europe, both of which have 125 reference entities. These indices commonly have maturities of 3, 5, 7, and 10 years.
-
Example: An investor buying protection on the 5-year iTraxx Europe index at an ask price of 152 bps for €500,000 per firm would make total annual payments of 0.0152×€500,000×125=€950,000. If one reference entity defaults, the investor receives the appropriate payoff and a future reduction in annual payments of €7,600 (€950,000/125).
-
Practice Questions: Q1
Q1. The five-year CDX NA IG Index (125 companies) is quoted as bid 141 bps and ask 143 bps. An investor plans to sell $1 million of protection on each company. At the beginning of the third year before the annual protecon payment, one of the companies defaults. Assuming no other defaults, the investor’s cash flow for the third year is closest to:
A. $748,400 inflow.
B. $748,400 outflow.
C. $773,200 inflow.
D. $773,200 outflow.
Practice Questions: Q1 Answer
Explanation: A is correct.
The investor will sell CDS protection on the 125 companies in the index for 140 bps per company. The annual receipt by the seller is 0.0141 × $1,000,000 × 125 = $1,762,500. However, because one company defaulted before the protection payment, the annual receipt by the CDS seller will be reduced by $1,762,500 / 125 = $14,100. In addition, the seller will have to pay $1 million to the CDS protection
buyer as a result of the default. The CDS seller’s cash inflow for the year is computed as $1,762,500 - $14,100 - $1,000,000 = $748,400.
Topic 3. Fixed Coupons
- In a CDS contract, the protection buyer pays a regular fixed coupon to the protection seller in return for default protection. For investment-grade issuers, this fixed coupon is standardized to 100 basis points (1%) to simplify contract settlement and clearing. This standardized coupon is not necessarily the fair premium or CDS spread. An up-front premium may be paid to bridge the gap between the standardized fixed coupon and the fair CDS spread.
-
There are three possibilities for the up-front premium:
-
CDS spread = fixed coupon: No up-front premium is paid.
-
CDS spread > fixed coupon: The protection buyer pays an up-front premium equal to the present value of (CDS spread - fixed coupon).
-
CDS spread < fixed coupon: The protection seller pays an up-front premium to the protection buyer, equal to the present value of (fixed coupon - CDS spread).
-
Topic 4. CDS Spreads
-
The CDS spread is the price of the CDS, expressed in basis points. It represents the annual premium that the protection buyer pays to the protection seller for bearing the credit risk.
-
Relationship to Bond Yield Spread: In theory, the CDS spread should equal the bond yield spread, which is the difference between a corporate bond's yield and a comparable risk-free bond's yield.
-
Arbitrage: If the CDS spread and bond yield spread are not equal, an arbitrage opportunity may exist:
-
CDS spread < bond yield spread: Buy the corporate bond and buy CDS protection to earn more than the risk-free rate.
-
CDS spread > bond yield spread: Sell the corporate bond and sell CDS protection to borrow at less than the risk-free rate.
-
-
Practice Questions: Q2
Q2. In the context of arbitrage trades, if the CDS spread is significantly greater than the bond yield spread, what is the most appropriate action by the investor?
A. Buy the corporate bond and buy CDS protection.
B. Buy the corporate bond and sell CDS protection.
C. Sell the corporate bond and buy CDS protection.
D. Sell the corporate bond and sell CDS protection.
Practice Questions: Q2 Answer
Explanation: D is correct.
If the CDS spread is greater than the bond yield spread, sell the corporate bond, and sell CDS protection to borrow at less than the risk-free rate.
Topic 5. CDS-Bond Basis
-
The CDS-bond basis is defined as the difference between the CDS spread and the bond yield spread. While it should theoretically be zero, in practice it is often non-zero due to several factors.
-
Reasons for a Non-Zero Basis:
-
Bonds trading significantly above or below par.
-
Counterparty risk in CDS contracts (negative basis).
-
The possibility of a cheapest-to-deliver (CTD) bond in a CDS (positive basis).
-
CDS payoffs excluding accrued interest (negative basis).
-
Restructuring clauses in CDS contracts (positive basis).
-
Different risk-free rates being used to compute the spreads.
-
Illiquidity, which prevents full exploitation of arbitrage opportunities.
-
-
- The basis was generally positive before the 2007-2009 financial crisis but has since become negative and less significant.
Topic 6. Approximating Hazard Rates
- An approximate calculation for the average hazard rate can be derived from credit spreads for a bond trading near par value.
-
-
s(T) is the credit spread for maturity T.
-
RR is the recovery rate.
-
-
Example: With a 5-year credit spread of 210 bps (2.1%) and a recovery rate of 30%, the average annual hazard rate is 0.021/(1−0.3)=3%.
-
Bootstrapping a Term Structure: This method can be used to determine a term structure of hazard rates from credit spreads for different maturities.
-
For a 3-year spread of 80 bps and a 65% recovery rate, the average 3-year hazard rate is 0.008/(1−0.65)=2.29%.
-
For a 5-year spread of 90 bps and 65% recovery, the average 5-year hazard rate is 0.009/(1−0.65)=2.57%.
-
The average hazard rate between Year 3 and Year 5 is then [(5×0.0257)−(3×0.0229)]/2=2.99%.
-
Topic 7. More Precise Hazard Rates
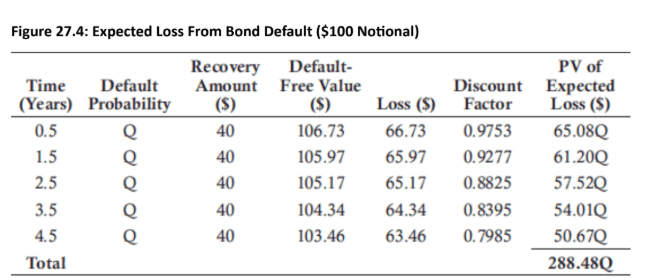
- For bonds that do not trade near their par value, a more precise calculation is required. This involves comparing the price of a risky corporate bond to a comparable risk-free government bond. The difference in their prices represents the expected loss from default over the bond's term. The present value of the expected loss is calculated based on assumed default probabilities at specific times, usually before coupon payment dates. The default probability (Q) is assumed to be constant over the bond's life.
Module 3. Comparing Default Probabilities

Topic 1. Historical Default Probabilities Vs Credit Yield Spreads
Topic 2. Real-World vs. Risk-Neutral Default Probabilities
Topic 3. Default Probability Estimation with the Merton Model
Topic 4. Merton Model Performance



Topic 1. Historical Default Probabilities Vs Credit Yield Spreads
-
Two Approaches to Estimating Default Probabilities
-
Historical Default Probabilities: These are based on past data, such as rating migration matrices, which show the frequency of defaults for different credit ratings over time. This approach provides a real-world estimate of default probabilities.
-
Credit Yield Spreads (Risk-Neutral Probabilities): These probabilities are derived from market prices of bonds or credit default swaps (CDS). A higher credit spread implies a higher perceived risk of default. This approach yields a risk-neutral probability of default, which is the probability that makes the expected return on a risky asset equal to the risk-free rate.
-
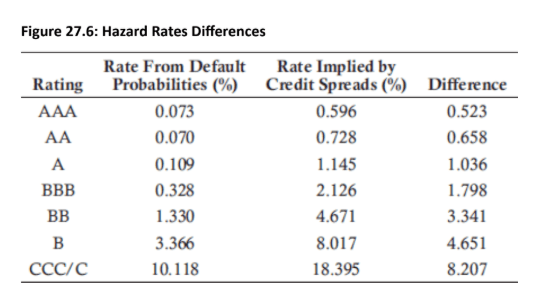
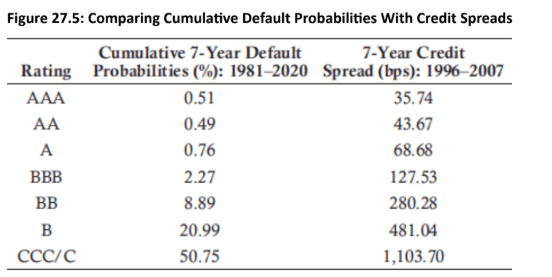
Topic 1. Historical Default Probabilities Vs Credit Yield Spreads
Topic 2. Real-World vs. Risk-Neutral Default Probabilities
-
Understanding the Difference
-
Real-World Default Probabilities: These are objective probabilities of default that can be estimated from historical data. They are useful for credit risk management, portfolio credit value at risk (VaR), and calculating expected losses.
-
Risk-Neutral Default Probabilities: These probabilities are not true default probabilities but are derived from financial market prices. They are used for pricing financial instruments like credit default swaps and other credit derivatives.
-
Key Distinction: Risk-neutral probabilities are higher than real-world probabilities. This is because market prices incorporate a risk premium to compensate investors for bearing credit risk.
-
Why it Matters: A company's credit value at risk is calculated using real-world default probabilities and is used to determine counterparty credit risk. However, the pricing of a CDS is based on risk-neutral probabilities.
-
Topic 3. Default Probability Estimation with the Merton Model
-
Introduction to the Merton Model
-
Core Idea: The Merton model treats a company's equity as a call option on the company's assets. The shareholders (equity holders) have the right to acquire the company's assets by paying off the debt (the strike price of the option). If the value of the assets is less than the value of the debt at maturity, the shareholders will not exercise their "option" and will default on the debt.
-
Key Variables: The model uses the following variables to compute default probability:
-
Firm's Asset Value (V): The total value of the company's assets.
-
Firm's Debt (D): The book value of the company's total liabilities.
-
Time to Maturity (T): The time until the debt matures.
-
Volatility of Assets (σV): The volatility of the firm's asset value.
-
Risk-Free Rate (r): The risk-free interest rate.
-
-
-
Calculating Key Metrics with the Merton Model
-
Distance to Default (DD): This is a measure of how many standard deviations the firm's asset value is from its debt level.
-
-
Probability of Default (PD): The PD is derived from the distance to default. It is the probability that the value of the firm's assets will fall below the face value of its debt at maturity.
-
PD=N(−DD)
-
Where N(x) is the cumulative standard normal distribution function.
-
-
Equity Value (E): The value of equity is a function of the firm's asset value, debt, and the volatility of its assets. It is calculated using the Black-Scholes-Merton option pricing model.
Topic 3. Default Probability Estimation with the Merton Model
Practice Questions: Q1
Q1. A junior analyst is evaluating the following questions to include in her research report:
- Which type of default probabilities should be used in valuation?
- What is the impact on a company defaulting when the distance to default rises?
Regarding these questions, the analyst’s report should support which of the following conclusions?

Practice Questions: Q3 Answer
Explanation: B is correct.
Risk-neutral default probabilities should be used in valuation, and real-world default probabilities should be used in scenario analysis. As the distance to default rises (falls), the company is less (more) likely to default.
Topic 4. Merton Model Performance
-
Advantages and Disadvantages
-
Advantages:
Intuitive Framework: The model provides a clear, intuitive link between a company's financial structure and its default risk.
Forward-Looking: It is a forward-looking model that uses market prices, unlike historical default rates.
Consistent: It provides a consistent framework for valuing both a company's equity and its debt.
-
Disadvantages:
Assumptions: The model relies on strong assumptions, such as a single class of debt, a simplified balance sheet, and a single maturity date.
Asset Volatility: The volatility of a firm's assets is not directly observable and must be estimated, which can be challenging and a source of error.
Market Value of Liabilities: The model uses the book value of total liabilities, which may not accurately reflect the market value.
-
Conclusion: The Merton model is a valuable theoretical tool for understanding default risk and is used in a variety of contexts, but its practical application is limited by its simplifying assumptions and the need to estimate key parameters.
CR 9. Estimating Default Probabilities
By Prateek Yadav
CR 9. Estimating Default Probabilities
- 104



