What is Big O?

• Big O notation is used to describe the performance or complexity of an algorithm.
• Big O specifically describes the worst-case scenario.
• Used to describe the execution time required or the space used by an algorithm.

Big O complexity can be visualized with this graph

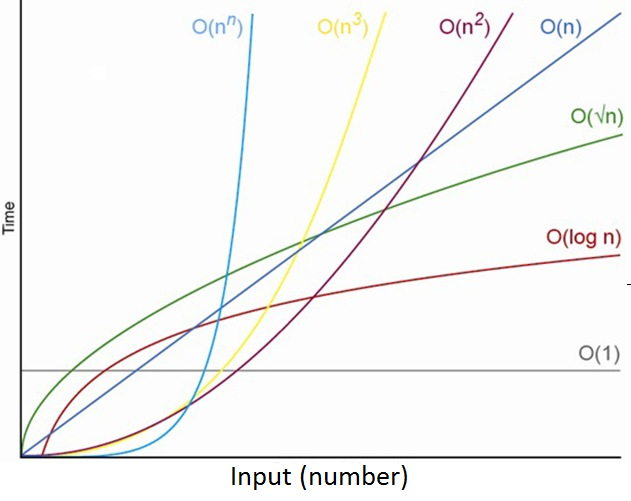
Algorithm's Scale as follows...

*listed in order of complexity

O(1)

• O(1) describes an algorithm that will always execute in the same time regardless of the size of the input data set.

constant complexity

// For example, accessing any single element in an array takes 
// constant time as only one operation has to be performed to locate it.

var arr = [ 'accessing', 'an', 'array', 'element', 'takes', 'constant', 'time']
var index = arr[4] // return 'takes'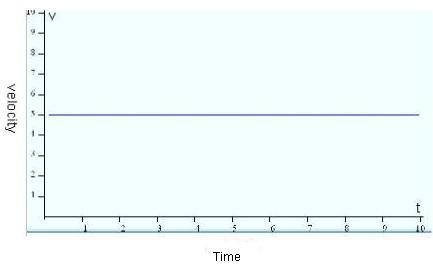

O(N)

• O(N) describes an algorithm whose performance will grow linearly and in direct proportion to the size of the input data set.

Linear complexity

// For example, a procedure that 
// adds up all elements 
// of a list requires time 
// proportional to the length of the list.

var start= new Date().getTime();

var arr = []
var j = 0;

while ( j < 100000 ) {
    arr.push(j);
    j++;
}

var sum = 0;

for ( var i = 0; i < arr.length; i++ ) {
    sum += arr100[i];
}

var end = new Date().getTime();
var time = end - start;
console.log('Execution time: ' + time);

O(     )

• O(     ) represents an algorithm whose performance is directly proportional to the square of the size of the input data set.

quadratic time

// This is common with algorithms 
// that involve nested iterations 
//over the data set. Deeper nested 
//iterations will result in O(N3), O(N4) etc.

var grid = document.createElement('table');
grid.className = 'grid';

for (var r = 0; r < this._rows; ++r) {
  var tr = grid.appendChild(document.createElement('tr'));

  for (var c = 0; c < this._cols; ++c) {

    var cell = tr.appendChild(document.createElement('td'));
    cell.id = "grid" + i++
  }
}

O(     )

• O(     ) The growth curve of an O(     ) function is exponential - starting off very shallow, then rising meteorically.

exponential time

// An example of this is trying to break a password by testing 
// every possible combination (assuming numerical 
// password of length N). This results in O(10^N) complexity.

O( log N )

• Algorithms taking logarithmic time are commonly found in operations on binary trees or when using binary search.
• An O(log n) algorithm is considered highly efficient, as the operations per instance required to complete decrease with each instance.

logarithmic time

O( log N )

Continued...

// An example of logarithmic algorithm is an algorithm that cuts 
// a string in half, then cuts the right half in half, and so on. It will take 
// O(log n) time (n being the length of the string) since we chop the string 
// in half before each print

// Function to recursively print the right half of a string
var right = function(str){
    var length = str.length;
    
    // Helper function
    var help = function(index){
        
        // Recursive Case: Print right half
        if(index < length){
          
            // Prints characters from index until the end of the array
            console.log(str.substring(index, length));
            
            // Recursive Call: call help on right half
            help(Math.ceil((length + index)/2));
        }
        
        // Base Case: Do Nothing
    }
    help(0);
}