\text{Chapter 17}
\text{Chapter 17}
\text{Chapter 17}
\text{Chapter 17}
\text{Dr. Adel Abbout}
\displaystyle {\Delta \phi}= \frac{2 \pi }{\lambda} \Delta L
\text{constructive interference}
\text{destructive interference}
\Delta L=n\lambda
\Delta L=(2n+1)\frac{\lambda}{2}
\Delta \phi=n 2\pi
\Delta \phi=(2n +1)\pi
\text{The pressure in a travelling sound wave is given by the equation}
\Delta \mathrm{p}=(1.00 \mathrm{~Pa}) \sin \pi\left[\left(0.900 \mathrm{~m}^{-1}\right) \mathrm{x}-\left(315 \mathrm{~s}^{-1}\right) \mathrm{t}\right]
\text{Find the sound level of the wave (Take the density of air $\rho_{\text {air }}=1.21 \mathrm{~kg} / \mathrm{m}^3$ ).}
\text{A) $90.7 \mathrm{~dB}$}
\text{B) $100 \mathrm{~dB}$}
\text{C) $85.0 \mathrm{~dB}$}
\text{D) $75.0 \mathrm{~dB}$}
\text{E) $120 \mathrm{~dB}$}
\beta=10 \log\frac{I}{I_0}
\quad I=\frac{1}{2} \rho v \omega^2 s_m^2
\Delta p_m=v \rho \omega s_m
I=\frac{1}{2} \frac{\Delta p_m^2}{\rho v}
\beta=10 \log \Bigg( \frac{1}{2} \frac{\Delta P_m^2}{\rho v I_0}\Bigg)=10 \log \Bigg(\frac{1}{2} \frac{1^2}{350\times1.21\times10^{-12}}\Bigg)
\beta=90.7 \mathrm{~dB}
v=\frac{\omega}{k}=\frac{315\pi}{0.9\pi}=350\text{ m/s}
\text{Answer A}
\text{The pressure in a travelling sound wave is given by the equation}
\Delta \mathrm{p}=(1.00 \mathrm{~Pa}) \sin \pi\left[\left(0.900 \mathrm{~m}^{-1}\right) \mathrm{x}-\left(315 \mathrm{~s}^{-1}\right) \mathrm{t}\right]
\text{Find the sound level of the wave (Take the density of air $\rho_{\text {air }}=1.21 \mathrm{~kg} / \mathrm{m}^3$ ).}
\text{Organ pipe A, with one open end, has a fundamental frequency of $220 \mathrm{~Hz}$. The next-highest }
\text{harmonic of pipe $A$ has the same frequency as the third harmonic of a pipe B which has both}
\text{ends open. How long is pipe B? The speed of sound $=345 \mathrm{~m} / \mathrm{s}$.}
\text{A) $0.784 \mathrm{~m}$}
\text{B) $0.321 \mathrm{~m}$}
\text{C) $0.732 \mathrm{~m}$}
\text{D) $0.214 \mathrm{~m}$}
\text{E) $0.136 \mathrm{~m}$}
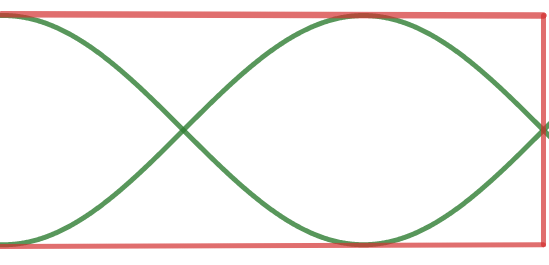
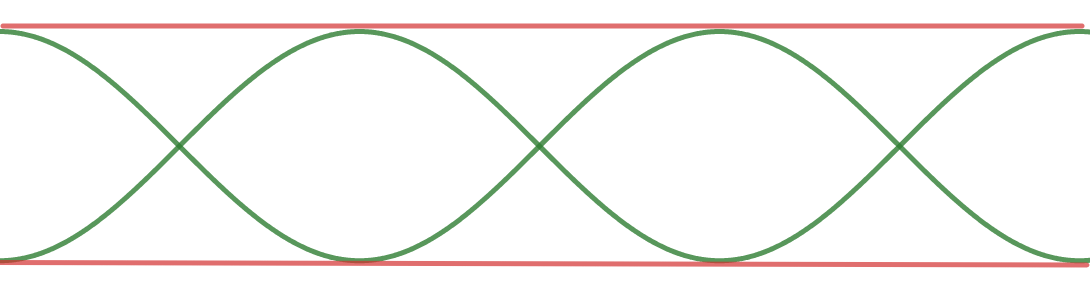
A
B
f_3^A=3f_1^A=660 \text{ Hz}
f_3^B=3\frac{v}{2L}
L=\frac{3}{2}\frac{345}{660}=0.784 \text{ m }
\text{The first harmonic of $A$ is $f_1$}
\text{the next harmonic is $f_3$ (because $f_2$ is missing)}
\text{For pipe $B$, the third harmonic is $f_3$}
f_3^A=f_3^B
3\frac{v}{2L}=660 \text{Hz}
\Rightarrow
\text{Organ pipe A, with one open end, has a fundamental frequency of $220 \mathrm{~Hz}$. The next-highest }
\text{harmonic of pipe $A$ has the same frequency as the third harmonic of a pipe B which has both}
\text{ends open. How long is pipe B? The speed of sound $=345 \mathrm{~m} / \mathrm{s}$.}
\text{third harmonic}
\text{third harmonic}
\text{(one closed end)}
\text{(two open ends)}
\text{Answer A}
\text{Two loudspeakers $S_1$ and $S_2$ are in phase and emit sound waves with the same frequency.}
\text{They are placed along the $y$-axis and are separated by a distance of $8.00 \mathrm{~m}$, as shown in}
\text{FIGURE 2. A person is standing at point $\mathrm{O}$ which is $12.0 \mathrm{~m}$ from the yaxis and equidistant }
\text{from the loudspeakers. When the person moves from point $\mathrm{O}$ to point $\mathrm{P}$ at a distance of $3 \mathrm{~m}$,}
\text{he detects the second destructive interference in sound intensity.}
\text{What is the frequency of the sound waves emitted by the loudspeakers? }
\text{The speed of sound in air is $343 \mathrm{~m} / \mathrm{s}$}
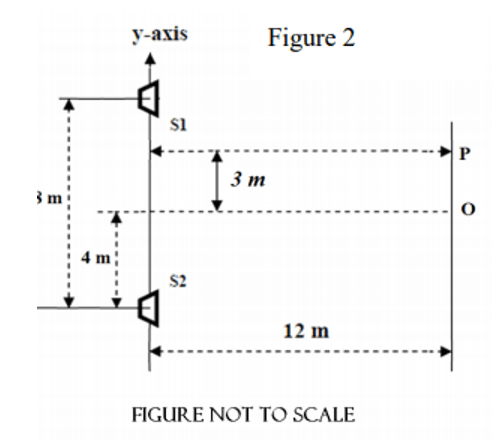
8 \text{ m}
\text{A) $278 \mathrm{~Hz}$}
\text{B) $178 \mathrm{~Hz}$}
\text{C) $222 \mathrm{~Hz}$}
\text{D) $335 \mathrm{~Hz}$}
\text{E) $522 \mathrm{~Hz}$}
\text{Two loudspeakers $S_1$ and $S_2$ are in phase and emit sound waves with the same frequency.}
\text{They are placed along the $y$-axis and are separated by a distance of $8.00 \mathrm{~m}$, as shown in}
\text{FIGURE 2. A person is standing at point $\mathrm{O}$ which is $12.0 \mathrm{~m}$ from the yaxis and equidistant }
\text{from the loudspeakers. When the person moves from point $\mathrm{O}$ to point $\mathrm{P}$ at a distance of $3 \mathrm{~m}$,}
\text{he detects the second destructive interference in sound intensity.}
\text{What is the frequency of the sound waves emitted by the loudspeakers? }
\text{The speed of sound in air is $343 \mathrm{~m} / \mathrm{s}$}

\begin{aligned}
& \mathrm{L}_2=\sqrt{12^2+7^2}=13.89 \mathrm{~m} \\
& \mathrm{~L}_1=\sqrt{12^2+1^2}=12.01 \mathrm{~m} \\
& \Delta \mathrm{L}=13.89-12.01=1.849 \mathrm{~m} \\
& \Delta \mathrm{L}=\frac{3 \lambda}{2} \\
& \lambda=\frac{2 \Delta \mathrm{L}}{3}=\frac{2 \times 1.849}{3}=1.23 \mathrm{~m} \\
& \mathrm{f}=\frac{\mathrm{v}}{\lambda}=\frac{343}{1.23}=278 \mathrm{~Hz}
\end{aligned}
L_1
L_2
8 \text{ m}
\text{(second destructive interference)}
\text{Answer A}
\text{A sound meter placed $3.0 \mathrm{~m}$ from a point sound source registers a sound level of 80 $\mathrm{dB}$.}
\text{What sound level will the sound meter register if the power of the source is reduced by }
\text{a factor of 25 ?}
\text{A) $66 \mathrm{~dB}$}
\text{B) $11 \mathrm{~dB}$}
\text{C) $32 \mathrm{~dB}$}
\text{D) $3.2 \mathrm{~dB}$}
\text{E) $55 \mathrm{~dB}$}
\frac{P_f}{P_i}=\frac{I_f/A}{I_i/A}=\frac{I_f}{I_i}=\frac{1}{25}
\Delta \beta=10 \log \left(\frac{I_f}{I_0}\right)-10 \log \left(\frac{I_i}{I_0}\right)=10 \log \left(\frac{I_f}{I_i}\right)=10 \log \left(\frac{1}{25}\right)=-13.97
\beta_{\mathrm{f}}=\beta_{\mathrm{i}}+\Delta \beta=80-13.97=66.03 \mathrm{~dB}
\text{The area $A$ of the sound meter is the same, so we can deduce that:}
\log a-\log b=\log \frac{a}{b}
\text{we recall that}
\text{A sound meter placed $3.0 \mathrm{~m}$ from a point sound source registers a sound level of 80 $\mathrm{dB}$.}
\text{What sound level will the sound meter register if the power of the source is reduced by }
\text{a factor of 25 ?}
\text{The sound level at a distance of $3.0 \mathrm{~m}$ from a point source is $120 \mathrm{~dB}$. At what distance is the }
\text{sound level $100 \mathrm{~dB}$ ?}
\text{A) $30 \mathrm{~m}$}
\text{B) $9.0 \mathrm{~m}$}
\text{C) $65 \mathrm{~m}$}
\text{D) $6.0 \mathrm{~m}$}
\text{E) $12 \mathrm{~m}$}
\beta_1=10(\text{dB}) \log \left(I_1 /I_0\right), \beta_2=10(\text{dB}) \log \left(I_2/ I_0\right)
\beta_1-\beta_2=10(\text{dB}) \log \left(\frac{I_1}{I_2}\right) \Rightarrow \frac{20}{10}=\log \left(\frac{P}{4 \pi R_1^2} \times \frac{4 \pi R_2^2}{P}\right)
\Rightarrow 2 \log \left(\frac{R_2}{R_1}\right)=2 \Rightarrow \frac{R_2}{R_1}=10^1 \Rightarrow R_2=10 \times 3=30 \mathrm{~m}
\text{The sound level at a distance of $3.0 \mathrm{~m}$ from a point source is $120 \mathrm{~dB}$. At what distance is the }
\text{sound level $100 \mathrm{~dB}$ ?}
\text{A car is approaching a reflecting wall with speed $V_c$. A stationary observer behind the car hears }
\text{a sound of frequency $828 \mathrm{~Hz}$ directly from the car horn and a sound of frequency $971 \mathrm{~Hz}$ reflected }
\text{from the wall, as shown in the FIGURE 5. Find the speed $V_c$ of the car. }
\text{A) $27.3 \mathrm{~m} / \mathrm{s}$}
\text{B) $40.2 \mathrm{~m} / \mathrm{s}$}
\text{C) $12.5 \mathrm{~m} / \mathrm{s}$}
\text{D) $49.0 \mathrm{~m} / \mathrm{s}$}
\text{E) $32.3 \mathrm{~m} / \mathrm{s}$}
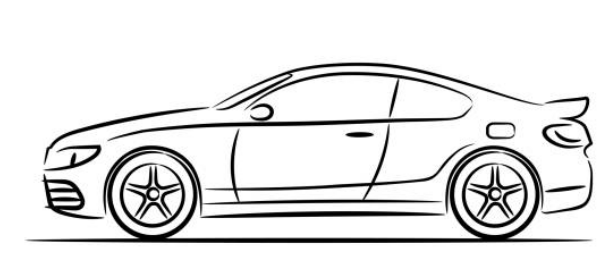


V_c
\text{reflecting wall}
\text{Stationary}\\
\text{observer}
\text{A car is approaching a reflecting wall with speed $v_c$. A stationary observer behind the car hears }
\text{a sound of frequency $828 \mathrm{~Hz}$ directly from the car horn and a sound of frequency $971 \mathrm{~Hz}$ reflected }
\text{from the wall, as shown in the FIGURE 5. Find the speed $v_c$ of the car. }
828(v+v_c)=971(v-v_c)
1) \text{car (\textcolor{red}{source}) approaches the wall }
f'=f\frac{v-0}{v-v_c}=971 \text{ Hz}
\text{after reflection from the wall, the wall becomes a \textcolor{red}{source} and the person \textcolor{red}{detector}, so he hears $f'$}
2) \text{car (\textcolor{red}{source}) runs away from the person \textcolor{red}{(detector)} }
f''=f\frac{v-0}{v+v_c}=828 \text{ Hz}
(828+971)v_c=(971-828)v
v_c=\frac{143}{1799}\times343\approx{27.3} \text{ m/s}
\frac{f''}{f'}=\frac{828}{971}=\displaystyle \frac{\displaystyle \frac{v}{v+v_c}}{\displaystyle \frac{v}{v-v_c}}=\frac{v-v_c}{v+v_c}



V_c
\text{reflecting wall}
\text{Stationary}\\
\text{observer}
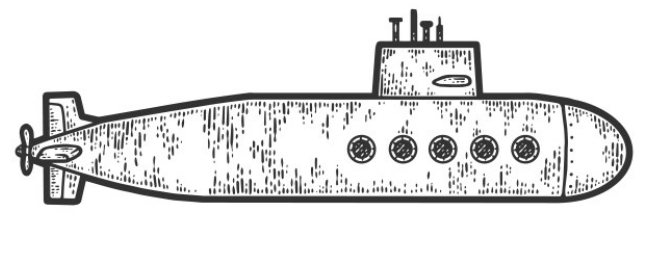
\text{In Figure 2, submarine A and submarine B move toward each other in motionless water in the }
\text{Atlantic Ocean. Submarine A moves at speed $v_A=50.0 \mathrm{~km} / \mathrm{h}$, and the submarine B at }
\text{$v_B=70.0$ $\mathrm{km} / \mathrm{h}$. Submarine A sends out a sonar signal (sound wave in water) at $1.00 \times 10^3 \mathrm{~Hz}$.}
\text{Sonar waves travel at $5470 \mathrm{~km} / \mathrm{h}$. What is the signal's frequency as detected by submarine B? }
\text{A) $1.02 \hspace{1mm}\mathrm{ kHz}$}
\text{B) $2.16\hspace{1mm} \mathrm{kHz}$}
\text{C) $4.02\hspace{1mm} \mathrm{kHz}$}
\text{D) $3.34 \hspace{1mm}\mathrm{kHz}$}
\text{E) $5.22\hspace{1mm} \mathrm{kHz}$}

A
B
v_A
v_B


\text{reflected}
\text{In Figure 2, submarine A and submarine B move toward each other in motionless water in the }
\text{Atlantic Ocean. Submarine A moves at speed $v_A=50.0 \mathrm{~km} / \mathrm{h}$, and the submarine B at }
\text{$v_B=70.0$ $\mathrm{km} / \mathrm{h}$. Submarine A sends out a sonar signal (sound wave in water) at $1.00 \times 10^3 \mathrm{~Hz}$.}
\text{Sonar waves travel at $5470 \mathrm{~km} / \mathrm{h}$. What is the signal's frequency as detected by submarine B? }
f_B=f_A\left(\frac{v + v_B}{v - v_s}\right)=1000\left(\frac{5470+70}{5470-50}\right)=1.02 \times 10^3 \mathrm{~Hz}
\text{Source: A}
\text{Detector: B}


A
B
v_A
v_B


\text{reflected}
\text{A bat emits sound at a frequency of $3.00 \times 10^4 \mathrm{~Hz}$ as it approaches a wall. The frequency of the}
\text{sound reflected from the wall and detected by the bat is $3.09 \times 10^4 \mathrm{~Hz}$. What is the speed of }
\text{the bat? The speed of sound in air is $343 \mathrm{~m} / \mathrm{s}$. }
\begin{gathered}
\text{A) 5.07 m/s} \\
\text{B) 3.50 m/s} \\
\text{C) 2.20 m/s} \\
\text{D) 6.30 m/s}\\
\text{E) 7.70 m/s}
\end{gathered}
\text{A bat emits sound at a frequency of $3.00 \times 10^4 \mathrm{~Hz}$ as it approaches a wall. The frequency of the}
\text{sound reflected from the wall and detected by the bat is $3.09 \times 10^4 \mathrm{~Hz}$. What is the speed of }
\text{the bat? The speed of sound in air is $343 \mathrm{~m} / \mathrm{s}$. }
{f}^{\prime \prime}=f\left(\frac{\mathrm{v}+\mathrm{v}_{\text {bat }}}{\mathrm{v}-v_{\text {bat }}}\right)
\frac{f^{\prime \prime}}{f}=\frac{3.09 \times 10^4}{3 \times 10^4}=1.03=\frac{\mathrm{v}+v_{\text {bat }}}{v-v_{\text {bat }}}
1.03\left(\mathrm{v}-\mathrm{v}_{\text {bat }}\right)=\mathrm{v}+\mathrm{v}_{\text {bat }} \Rightarrow 0.03 \mathrm{v}=2.03 \mathrm{v}_{\text {bat }}
\mathrm{v}_{\text {bat }}=\frac{0.03 \times \mathrm{v}}{2.03}=\frac{0.03 \times 343}{2.03}=5.07 \mathrm{~m} / \mathrm{s}
\text{A wave doesn't change frequency when reflected by a static wall}
f'=f\frac{v-0}{v-v_\text{bat}}
1) \text{Source: bat, Detector: wall}
f''=f'\frac{v+v_\text{bat}}{v-0}
2) \text{Source: wall, Detector: bat}
\text{from the two equations we deduce that:}
\Rightarrow
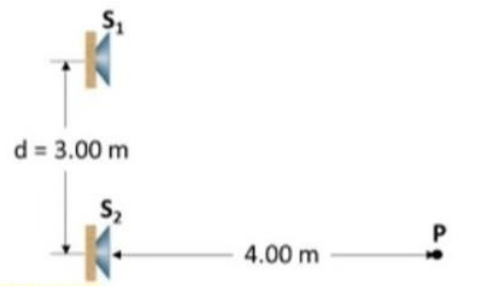
\text{In Figure 3, two identical speakers $S_1$ and $S_2$ emit in phase sound waves of frequency 434 Hz }
\text {If we switch on only one speaker, either $S_1$ or $S_2$, the level of sound at point $P$ is $20.0 \mathrm{~dB}$.}
\text{What will be the level of sound at $P$ if both speakers are switched on at the same time?}
\begin{aligned}
&\text{A) 26.0 dB} \\
&\text{B) 80.0 dB} \\
&\text{C) 40.0 dB} \\
&\text{D) 20.0 dB} \\
&\text{E) 15.0 dB}
\end{aligned}
\text{In Figure 3, two identical speakers $S_1$ and $S_2$ emit in phase sound waves of frequency 434 Hz }
\text {If we switch on only one speaker, either $S_1$ or $S_2$, the level of sound at point $P$ is $20.0 \mathrm{~dB}$.}
\text{What will be the level of sound at $P$ if both speakers are switched on at the same time?}

\Delta L=|L_1-L_2|=\sqrt{3^2+4^2}-4=1\text{ m}
\Delta \phi= \frac{2\pi}{\lambda} \Delta L=\frac{2\pi f}{v}\Delta L = \frac{2\pi \times343}{343}\times 1=2\pi
\text{with one source, the intensity is }
I=\frac{1}{2}\rho v \omega^2 s_m^2
\text{with two sources, we have interferences and a new amplitude $s'_m$}
I'=\frac{1}{2}\rho v \omega^2 {s'}_m^2
\text{with $s'_m=2 s_m \cos(\frac{\phi}{2})$}
\beta'-\beta=10\log \Big (I'/I_0\Big )-10\log \Big (I/I_0\Big )=10 \log \Big (I'/I\Big ) =10 \log \Big ({s'}^2_m/s_m^2\Big )
\beta'-\beta=10\log \Big(2^2\cos^2 \phi/2\Big)=10\log \Big(2^2\cos^2 \pi\Big)\approx 6
\text{(because $v=\lambda f$)}
\beta'=\beta+6=26 \text{ db}
\text{Answer A}
\text{Two speakers, placed $2.0 \mathrm{~m}$ apart, are in phase and emit sound waves with a frequency of $1000 \mathrm{~Hz}$.}
\text{Starting at the midpoint $\mathrm{P}$, a detector is moved along the line joining the two detectors toward}
\text{speaker A. How far (from the midpoint) should the detector move to observe the first maximum }
\text{in sound intensity? }
\text{A) $0.17 \mathrm{~m}$}
\text{B) $0.34 \mathrm{~m}$}
\text{C) $0.043 \mathrm{~m}$}
\text{D) $0.086 \mathrm{~m}$}
\text{E) $0.26 \mathrm{~m}$}
d/2-x
d/2+x



d=2.00 \text{ m}
S_1
S_2
x
A
B
\text{Two speakers, placed $2.0 \mathrm{~m}$ apart, are in phase and emit sound waves with a frequency of $1000 \mathrm{~Hz}$.}
\text{Starting at the midpoint $\mathrm{P}$, a detector is moved along the line joining the two detectors toward}
\text{speaker A. How far (from the midpoint) should the detector move to observe the first maximum }
\text{in sound intensity? }
d/2-x
d/2+x
\text{We suppose the first maximum appears at a distance $x$ from the middle}
L_1=d/2-x
L_2=d/2+x
\Delta L=L_2-L_1=2x
\text{first constructive interference: }
\Delta L=\lambda \Rightarrow 2x=\lambda \Rightarrow x=\lambda/2= v/2f=343/(2\times 1000)=0.17 \text{ m}



d=2.00 \text{ m}
S_1
S_2
x
A
B
\text{Two sound waves, from two different sources with the same frequency, $540 \mathrm{~Hz}$, travel in air }
\text{in the same direction. The sources are in phase. What is the phase difference of the waves }
\text{at a point that is $4.40 \mathrm{~m}$ from one source and $4.00 \mathrm{~m}$ from the other? }
\begin{array}{c}\text{A) 227}^\circ\\\text{B) 158}^\circ\\\text{C) 340}^\circ\\\text{D) 401}^\circ\\\text{E) 635}^\circ\end{array}
\text{Two sound waves, from two different sources with the same frequency, $540 \mathrm{~Hz}$, travel in air }
\text{in the same direction. The sources are in phase. What is the phase difference of the waves }
\text{at a point that is $4.40 \mathrm{~m}$ from one source and $4.00 \mathrm{~m}$ from the other? }
\displaystyle \frac{\Delta \phi}{2 \pi}=\frac{\Delta L}{\lambda} \quad \Rightarrow \Delta \phi=\frac{(4.4-4)}{v} \times f=\frac{0.4}{343} \times 540=3.95 \mathrm{rad}=227^0
\frac{\Delta \phi}{2 \pi}=\frac{\Delta L}{\lambda}
\text{because $v=\lambda f$}
\text{the speed of sound is a constant that can be found in the formula sheet: $v=343 \text{ m/s}$}
Chapter 17
By smstry
Chapter 17
- 682



