\int_0^\infty \sin(x)dx
\begin{gathered}
\mathbf{S}_i^{t+\Delta t}=\mathbf{S}_i+\frac{1}{2}\left[\Delta \mathbf{S}+\Delta \mathbf{S}^{\prime}\right] \Delta t \\
\Delta \mathbf{S}^{\prime}=-\frac{\gamma}{1+\lambda^2}\left(\mathbf{S}_i^{\prime} \times \mathbf{H}_{\mathrm{eff}}^{i^{\prime}}+\lambda \mathbf{S}_i^{\prime} \times\left(\mathbf{S}_i^{\prime} \times \mathbf{H}_{\mathrm{eff}}^{i^{\prime}}\right)\right)
\end{gathered}
from numpy import real,imag,sin,cos,pi,zeros,random,array,cross,sqrt,exp,dot,arccos
from numpy.linalg import norm
import kwant
from matplotlib import pyplot
import tinyarray as ta
import scipy
import time
import tinyarray
import operator
from math import *
import numpy as np\text{I am here explaining magnetization dynamics}
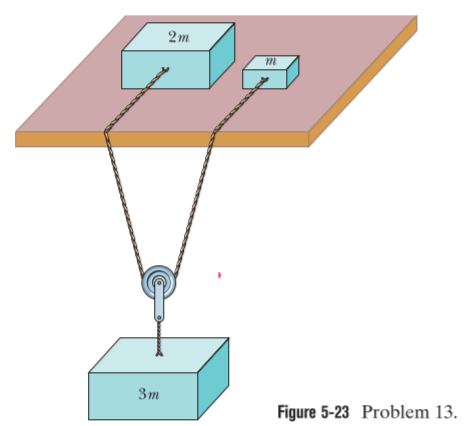
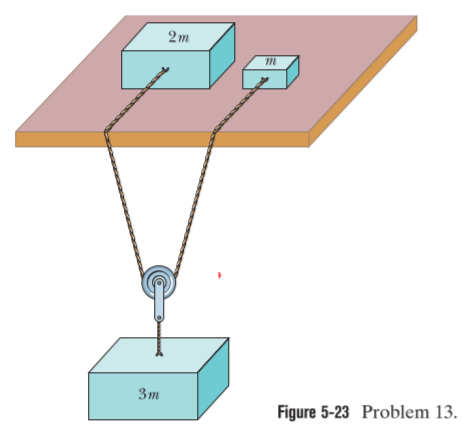
\vec{T}_1
\vec{T}_3
\vec{T}_4
\vec{T}_2
m\vec{g}
5 \text{ cm}
5 \text{ cm}
10 \text{ cm}
\vec{B}
30^0
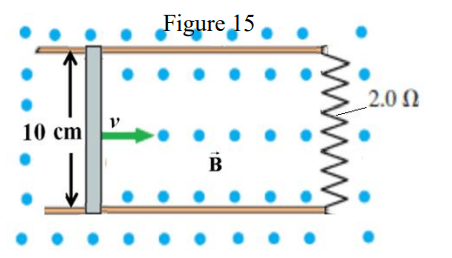
2.0 \text{ }\Omega
\vec{B}
v
10 \text{ cm}

\int_o^\infty
Q16.
\text{A frictionless pulley is in the form of a solid disk of mass 3.0 kg and radius 25 cm .}
deck
By smstry
deck
- 178



