0.003
0.006
0.009
1\times10^5
P_0
V(m^3)
P(Pa)
a
b
\sigma_1
\sigma_2
P
\cdot
\vec{E}=3.4\times 10^4 \hat{ i} \text{ N/C}
q
q
q'
q'


A/4
3A/4
\kappa_1
\kappa_2


A/4
3A/4
\kappa_1
\kappa_2
d


A/4
3A/4
\kappa_1
\kappa_2
d




+
-
R_1
R_2
R_3
R_4
\xi
i_2




6.00 \text{ V}
4.00 \text{ }\Omega
i_2
30 V
20V
10V
6.0k\Omega
2.0k\Omega
4.0k\Omega
i

R=2\Omega
\vec{v}



30 V
R
a
\cdot
\cdot
b
R
R
+
-
C
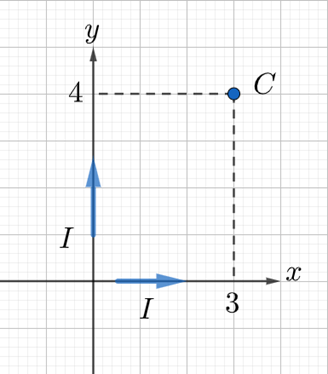
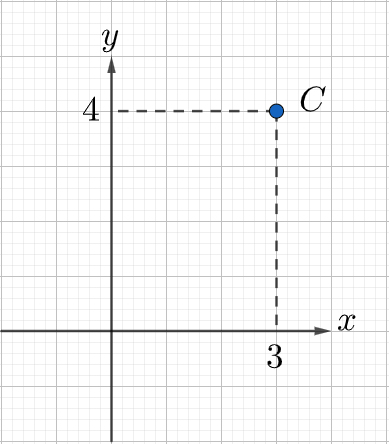
I
I
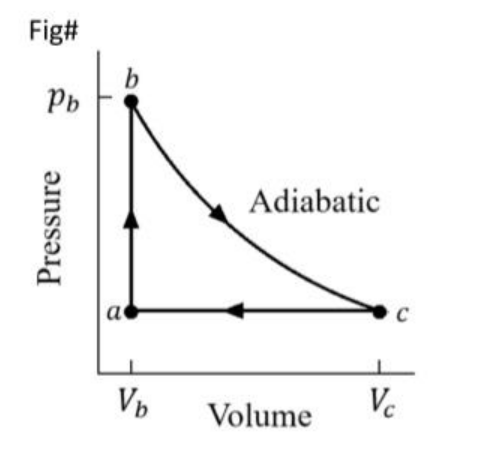
Q_p
Q_V
\Delta E=0=Q-W
Q=W
Q_V+Q_L=W
\epsilon=\frac{W}{Q_V}=\frac{Q_p+Q_V}{Q_V}={1+\frac{Q_P}{Q_V}}
\text{efficiency=What we get/What we inject}
\epsilon=1+\frac{n c_p \Delta T_p}{nc_v \Delta T_v}=1+{\gamma}\frac{\Delta T_p}{ \Delta T_V}
\epsilon=1+{\gamma}\frac{\Delta T_p}{ \Delta T_V}=1+{\gamma}\frac{P_a(V_a-V_c)}{V_a(P_b-P_a)}
\epsilon=1+\frac{1}{\gamma}\frac{V_a(P_b-P_a)}{P_a(V_a-V_c)}=1+{5/3}\frac{0.313\times(1-8)}{1\times(10-0.313)}=0.62
(T=\frac{PV}{nR})
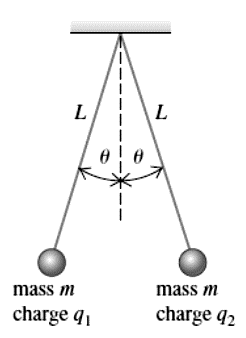
d
https://www.geogebra.org/material/iframe/id/ren4udsd/width/700/height/500/border/888888/sfsb/true/smb/false/stb/false/stbh/false
/ai/false/asb/false/sri/false/rc/true/ld/false/sdz/true/ctl/false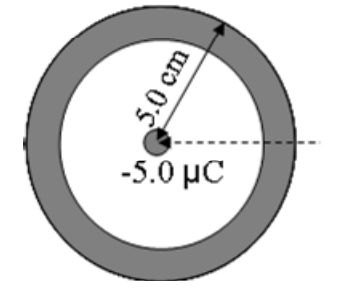

-6\hspace{1mm} \mu C




5.0 \text{ cm}
15 \text{ cm}
\cdot
P



d=3.00 \text{ m}
S_1
S_2
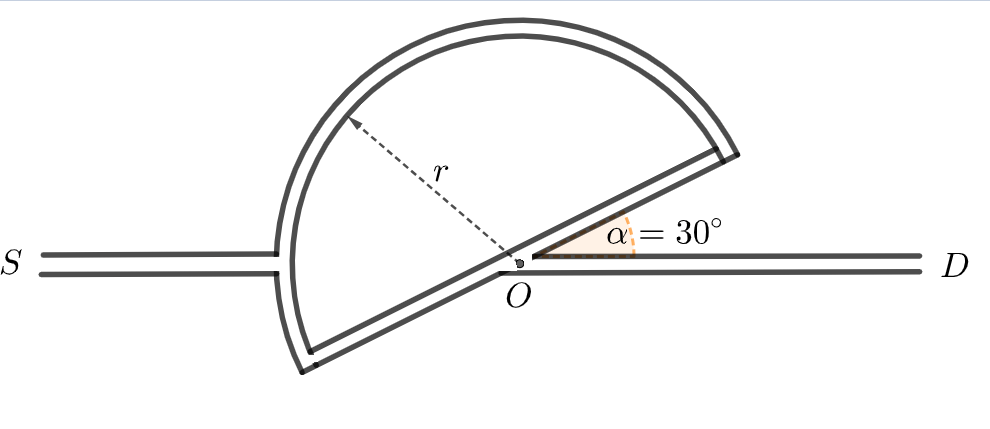
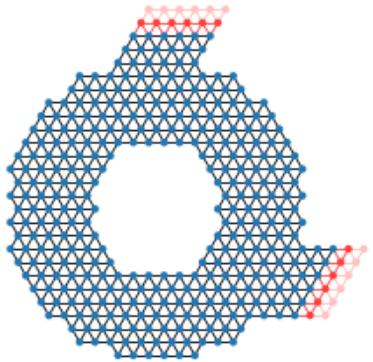
\cdot
\cdot
x(m)
y(m)
\cdot
P
+9\mu C
-5\mu C
d
d
d
d_2
d_1
\mathcal{A}
\mathcal{B}
\cdot
\cdot
q
2.00d
d
\infty
\theta_1
\cdot
q_1
q_2
Q
\theta_2
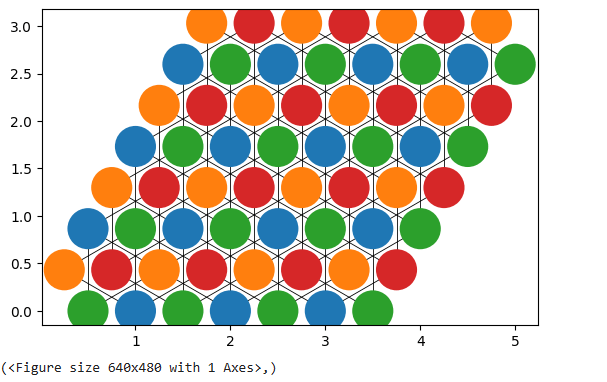
q
k
p
l
\cdot
\cdot
\cdot
\cdot
P
q_1
q_2
q_3
y
x
\theta
\theta
d
D
(0,0)
C_2
C_2
C_1
C_1
C_1
A
B
C_3
C_2
C_1
C_4
C_5
C_6
V
C_1=60\hspace{0.5mm}\mu F
42 \hspace{0.5mm}V
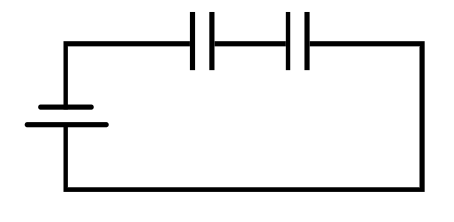
C_2= ?
C_1
\hspace{0.5mm}V

C_2
\Rightarrow

C_1
C_2
+
+
+
+
-
-
-
-

+
+
+
+
-
-
-
-

+
+
+
+
-
-
-
-

+
+
+
+
-
-
-
-
\Rightarrow

C_1
+
+
+
+
-
-
-
-

+
+
+
+
-
-
-
-

C_2
+
+
+
+
-
-
-
-

+
+
+
+
-
-
-
-
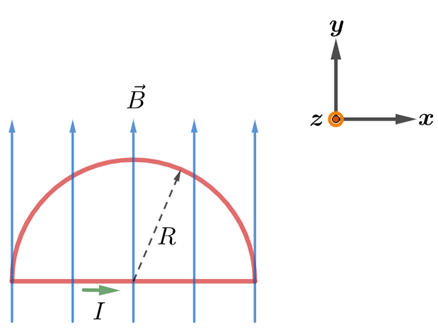


I
V
V
d
2d
deck
By smstry
deck
- 193



