\text{Chapter 9}

\textit{Dr. Adel Abbout}

\begin{align*} &\text{A } 3.0~\text{kg mass is positioned at } (0,\, 8.0)~\text{m, and a } 1.0~\text{kg mass is positioned at } (12,\, 0)~\text{m.} \nonumber \\ &\text{What are the coordinates of a } 4.0~\text{kg mass which will result in the center of mass of the system}\\ &\text{of three masses being located at the origin } (0,\, 0)? \nonumber \\[6pt] &\text{A) } (-12,\, -8.0)~\text{m} \quad\\ &\text{B) } (-3.0,\, -6.0)~\text{m} \quad\\ &\text{C) } (3.0,\, 6.0)~\text{m} \quad\\ &\text{D) } (-6.0,\, -3.0)~\text{m} \quad\\ &\text{E) } (-12,\, 0)~\text{m} \nonumber \end{align*}

\begin{align*} &\text{A } 3.0~\text{kg mass is positioned at } (0,\, 8.0)~\text{m, and a } 1.0~\text{kg mass is positioned at } (12,\, 0)~\text{m.} \nonumber \\ &\text{What are the coordinates of a } 4.0~\text{kg mass which will result in the center of mass of the system}\\ &\text{of three masses being located at the origin } (0,\, 0)? \nonumber \\[6pt] \end{align*}

\begin{aligned} & x_{\mathrm{cm}}=\frac{m_1 x_1+m_2 x_2+m_3 x_3}{m_1+m_2+m_3} \\ & y_{\mathrm{cm}}=\frac{m_1 y_1+m_2 y_2+m_3 y_3}{m_1+m_2+m_3} \end{aligned}

\text{The coordinates of the center of mass are:}

\left(x_{\mathrm{cm}}, y_{\mathrm{cm}}\right)=(0,0)

\text{We want }

\begin{gathered} 0=\frac{3(0)+1(12)+4 x_3}{8} \\ 12+4 x_3=0 \Rightarrow x_3=-3.0 \mathrm{~m} . \end{gathered}

\begin{gathered} 0=\frac{3(8)+1(0)+4 y_3}{8} \\ 24+4 y_3=0 \Rightarrow y_3=-6.0 \mathrm{~m} . \end{gathered}

\left(x_3, y_3\right)=(-3.0,-6.0) \mathrm{m}.

\text{Answer B}

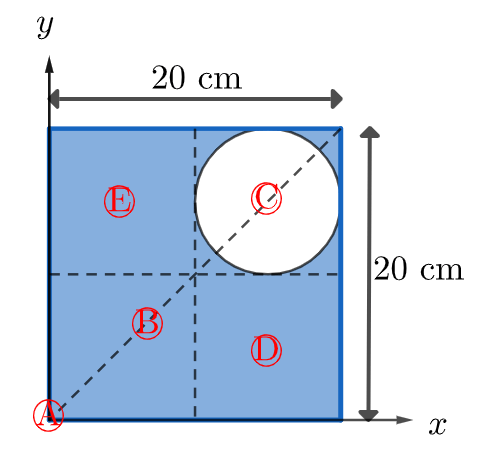
\begin{align*} &\text{A circular hole of radius } r = 5.0~\text{cm is cut from a uniform square metal sheet of side } 20~\text{cm},\\ &\text{as shown in Fig.~2.} \nonumber \\ &\text{Which point could be the center of mass of this sheet?} \nonumber \\[6pt] &\text{A) Point A} \quad \\ &\text{B) Point B} \quad \\ &\text{C) Point C} \quad \\ &\text{D) Point D} \quad \\ &\text{E) Point E} \nonumber \end{align*}

\begin{align*} &\text{A circular hole of radius } r = 5.0~\text{cm is cut from a uniform square metal sheet of side } 20~\text{cm},\\ &\text{as shown in Fig.~2.} \nonumber \\ &\text{Which point could be the center of mass of this sheet?} \nonumber \\[6pt] \end{align*}

\text{Answer B}

\text{The center of mass will be closer to where there is more mass}

\text{so, choices are \textcircled{A}, \textcircled{B} ,\textcircled{C}}

\begin{align*} &\text{A } 1.0~\text{kg particle is moving with a velocity of } 16~\text{m/s along the positive x-direction, while }\\ &\text{a } 3.0~\text{kg particle} \text{is moving with a velocity of } 4.0~\text{m/s along the positive y-direction.}\\ &\text{Find the magnitude of their center of mass velocity.} \nonumber \\ &\\ &\text{A) } 7.0~\text{m/s} \quad \\ &\text{B) } 4.0~\text{m/s} \quad \\ &\text{C) } 16~\text{m/s} \quad \\ &\text{D) } 5.0~\text{m/s} \quad \\ &\text{E) } 0 \nonumber \end{align*}

\begin{align*} &\text{A } 1.0~\text{kg particle is moving with a velocity of } 16~\text{m/s along the positive x-direction, while }\\ &\text{a } 3.0~\text{kg particle} \text{ is moving with a velocity of } 4.0~\text{m/s along the positive y-direction.}\\ &\text{Find the magnitude of their center of mass velocity.} \nonumber \\ &\\ \end{align*}

\begin{array}{ll} m_1=1.0 \mathrm{~kg}, & \vec{v}_1=(16,0) \mathrm{m} / \mathrm{s} \\ m_2=3.0 \mathrm{~kg}, & \vec{v}_2=(0,4.0) \mathrm{m} / \mathrm{s} \end{array}

\text{We have:}

\text{The formula for the center of mass is:}

\vec{v}_{\mathrm{cm}}=\frac{m_1 \vec{v}_1+m_2 \vec{v}_2}{m_1+m_2}

\begin{gathered} v_{\mathrm{cm}, x}=\frac{(1)(16)+(3)(0)}{1+3}=\frac{16}{4}=4.0 \mathrm{~m} / \mathrm{s} \\ v_{\mathrm{cm}, y}=\frac{(1)(0)+(3)(4)}{1+3}=\frac{12}{4}=3.0 \mathrm{~m} / \mathrm{s} \end{gathered}

\left|\vec{v}_{\mathrm{cm}}\right|=\sqrt{v_{\mathrm{cm}, x}^2+v_{\mathrm{cm}, y}^2}=\sqrt{4^2+3^2}=\sqrt{16+9}=5.0 \mathrm{~m} / \mathrm{s}

(\text{Answer D})

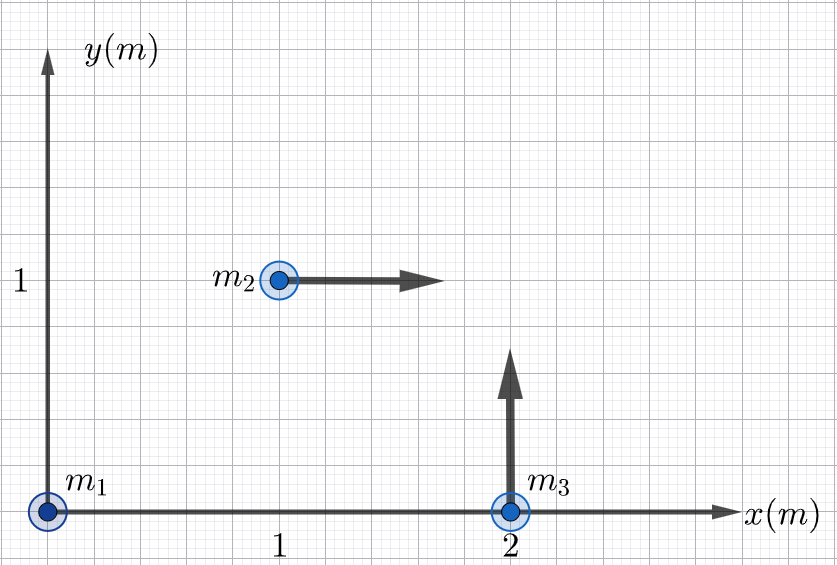
\begin{align*} &\text{Each object in Fig.~4 has a mass of } 2.0~\text{kg. The mass } m_1 \text{ is at rest, } m_2 \text{ has a speed of } 3.0~\text{m/s}\\ &\text{in the direction of } +x\text{-axis,} \text{ and } m_3 \text{ has a speed of } 6.0~\text{m/s in the direction of } +y\text{-axis.}\\ & \text{The momentum of the center of mass of the system is:} \nonumber \\ &\\ &\text{A) } (6.0\hat{i} + 12\hat{j})~\text{kg.m/s} \quad\\ &\text{B) } (1.0\hat{i} + 2.0\hat{j})~\text{kg.m/s} \quad\\ &\text{C) } (3.0\hat{i} + 6.0\hat{j})~\text{kg.m/s} \nonumber \\ &\text{D) } 3.0~\text{kg.m/s} \quad\\ &\text{E) } (-3.0\hat{i} + 6.0\hat{j})~\text{kg.m/s} \nonumber \end{align*}

\begin{align*} &\text{Each object in Fig.~4 has a mass of } 2.0~\text{kg. The mass } m_1 \text{ is at rest, } m_2 \text{ has a speed of } 3.0~\text{m/s}\\ &\text{in the direction of } +x\text{-axis,} \text{and } m_3 \text{ has a speed of } 6.0~\text{m/s in the direction of } +y\text{-axis.}\\ & \text{The momentum of the center of mass of the system is:} \nonumber \\ &\\ \end{align*}

\text{We have two ways to solve it: }

\vec{P}_{\mathrm{cm}}=M\vec{v}_\text{cm}

\begin{gathered} \vec{P}_{\text {total }}=\sum m_i \vec{v}_i \\ \vec{P}_{\text {total }}=m_1 \vec{v}_1+m_2 \vec{v}_2+m_3 \vec{v}_3 \end{gathered}

\vec{P}_{\text {total }}=(6 \hat{i}+12 \hat{j}) \mathrm{~kg} \cdot m/ \mathrm{s}

\text{where }M=m_1+m_2+m_3

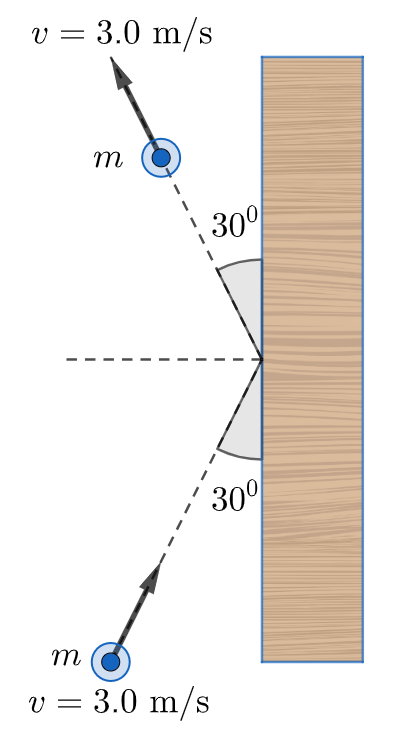
\begin{align*} &\text{A } 1.0~\text{kg ball strikes a vertical wall at an angle of } 30^\circ \text{ with a speed of } 3.0~\text{m/s} \text{ and bounces}\nonumber \\ &\text{off at the same angle with the same speed, as shown in Fig.~4. }\\ &\text{The change in momentum of the ball is:} \nonumber \\[6pt] &\text{A) } 6~\text{kg.m/s upward} \quad\\ &\text{B) } 9~\text{kg.m/s to the left} \quad\\ &\text{C) } 3~\text{kg.m/s to the right} \quad\\ &\text{D) } 0~\text{kg.m/s} \quad\\ &\text{E) } 3~\text{kg.m/s to the left} \nonumber \end{align*}

\begin{align*} &\text{A } 1.0~\text{kg ball strikes a vertical wall at an angle of } 30^\circ \text{ with a speed of } 3.0~\text{m/s} \text{ and bounces}\nonumber \\ &\text{off at the same angle with the same speed, as shown in Fig.~4. }\\ &\text{The change in momentum of the ball is:} \nonumber \\[6pt] \end{align*}

\Delta\vec{P}=m\vec{v_2}-m \vec{v_1}

\Delta \vec{P}=2mv \sin30^0 (-\hat{i})

=-2\times 1\times 3\times \frac{1}{2}\hat{i}=-3\hat{i} \text{ (kg.m/s)}

\text{(Answer E)}

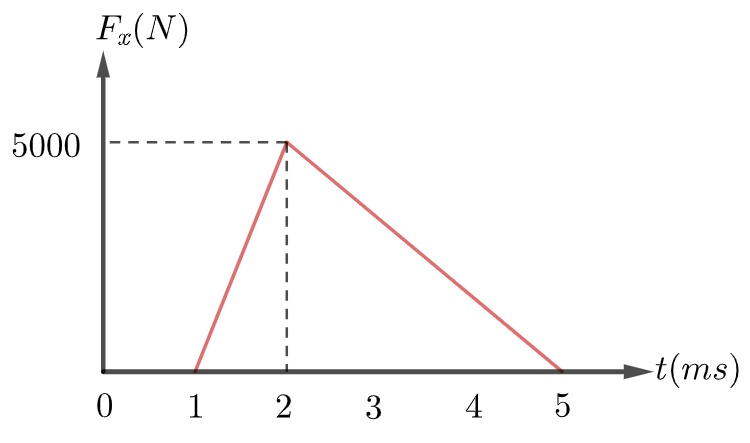
\begin{align*} &\text{An impulsive force } F_x \text{ as a function of time (in ms) is shown in Fig.~3, applied to an object }\\ &(m = 5.0~\text{kg}) \text{ at rest.} \text{ What will be its final speed?} \\ &\\ &\text{A) } 4.2~\text{m/s} \quad\\ &\text{B) } -3.2~\text{m/s} \quad\\ &\text{C) } 8.0~\text{m/s} \quad\\ &\text{D) } 16~\text{m/s} \quad\\ &\text{E) } 2.0~\text{m/s} \nonumber \end{align*}

\begin{align*} &\text{An impulsive force } F_x \text{ as a function of time (in ms) is shown in Fig.~3, applied to an object }\\ &(m = 5.0~\text{kg}) \text{ at rest.} \text{ What will be its final speed?} \\ \end{align*}

\text{The impulse is}

J=\int{F dt}=\text{Area under the curve}

J=\Delta P=P_f-P_i=P_f-0=P_f

P_f=\text{Area}=\frac{1}{2}4 (ms)\times 5000(N)=10 \mathrm{~N.s}

v_f=\frac{P_f}{m}=10/5=2 \mathrm{~m/s}

\text{(Answer E)}

\begin{align*} &\text{A } 1.0~\text{kg ball falling vertically hits a floor with a velocity of } 3.0~\text{m/s} \text{ and bounces vertically}\\ &\text{up with a velocity of } 2.0~\text{m/s.} \nonumber \\ &\text{If the ball is in contact with the floor for } 0.10~\text{s, the average force on the floor by the ball is:} \nonumber \\ &\\ &\text{A) } 50~\text{N down} \quad\\ &\text{B) } 30~\text{N down} \quad\\ &\text{C) } 0~\text{N} \quad\\ &\text{D) } 20~\text{N up} \quad\\ &\text{E) } 40~\text{N up} \nonumber \end{align*}

\begin{align*} &\text{A } 1.0~\text{kg ball falling vertically hits a floor with a velocity of } 3.0~\text{m/s} \text{ and bounces vertically}\\ &\text{up with a velocity of } 2.0~\text{m/s.} \nonumber \\ &\text{If the ball is in contact with the floor for } 0.10~\text{s, the average force on the floor by the ball is:} \nonumber \\ &\\ \end{align*}

\begin{align*} &\text{Change of velocity:}\\ &\\ & \hspace{3cm}\Delta v=v_f-v_i=2.0-(-3.0)=5.0 \mathrm{~m} / \mathrm{s}&\\ &\text{Change of momentum:}\\ &\\ &\hspace{3cm}\Delta p=m \Delta v=1.0 \times 5.0=5.0 \mathrm{~kg} \cdot \mathrm{~m} / \mathrm{s}\\ &\\ &\text{If we neglect gravity during the short contact (common approximation), the average} \\ &\text{force the ball exerts on the floor is}\\ &\\ &\hspace{3cm}F_{\mathrm{avg}} \approx \frac{\Delta p}{\Delta t}=\frac{5.0}{0.10}=50 \mathrm{~N} \end{align*}

\begin{align*} &\text{A } 0.5~\text{kg ball having velocity } (10\,\hat{i} + 10\,\hat{j})~\text{m/s collides and bounces off a wall with a velocity} \\ &\text{of } (-5.0\,\hat{i} + 10\,\hat{j})~\text{m/s. Find the average force on the ball if the collision time is } 0.01~\text{s.} \\[6pt] &\\ &\text{A) } (-200\,\hat{i})~\text{N} \quad\\ &\text{B) } (-250\,\hat{i})~\text{N} \quad\\ &\text{C) } (-750\,\hat{i})~\text{N} \quad\\ &\text{D) } (150\,\hat{i} + 200\,\hat{j})~\text{N} \quad\\ &\text{E) } (25\,\hat{i} + 100\,\hat{j})~\text{N} \\[6pt]\\ &\\[-4pt] \end{align*}

\begin{align*} &\text{A } 0.5~\text{kg ball having velocity } (10\,\hat{i} + 10\,\hat{j})~\text{m/s collides and bounces off a wall with a velocity} \\ &\text{of } (-5.0\,\hat{i} + 10\,\hat{j})~\text{m/s. Find the average force on the ball if the collision time is } 0.01~\text{s.} \\[6pt] \end{align*}

\begin{align*} &m = 0.5~\text{kg}, \quad \vec{u} = (10\,\hat{i} + 10\,\hat{j})~\text{m/s}, \quad \vec{v} = (-5\,\hat{i} + 10\,\hat{j})~\text{m/s}, \quad \Delta t = 0.01~\text{s}. \\[6pt] &\\[-4pt] &\text{The average force is given by:} \\[4pt] &\vec{F}_{\text{avg}} = \frac{m(\vec{v} - \vec{u})}{\Delta t} \\[6pt] &= \frac{0.5\left[(-5 - 10)\hat{i} + (10 - 10)\hat{j}\right]}{0.01} \\[6pt] &= \frac{0.5(-15\,\hat{i})}{0.01} \\[6pt] &= (-750\,\hat{i})~\text{N}. \\[6pt] &\\[-4pt] &\boxed{\vec{F}_{\text{avg}} = (-750\,\hat{i})~\text{N}} \\[6pt] \end{align*}

\begin{align*} &\text{A } 2.0~\text{kg block is given a single impulsive force in the positive } x\text{-direction as shown in Fig.~3.} \\ &\text{If the velocity of the block at } t = 0 \text{ was } -2.0~\text{m/s, find its velocity at } t = 5.0~\text{s.} \\[6pt] &\\[-4pt] &\text{A) } 6.0~\text{m/s} \quad\\ &\text{B) } 5.0~\text{m/s} \quad\\ &\text{C) } 2.0~\text{m/s} \quad\\ &\text{D) } 3.0~\text{m/s} \quad\\ &\text{E) } 1.0~\text{m/s} \\[6pt] &\\[-4pt] \end{align*}

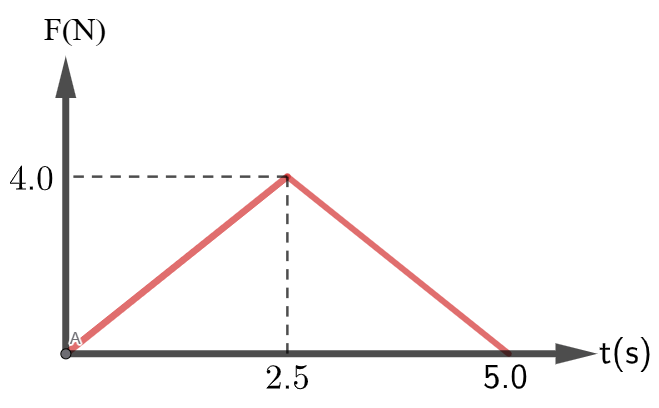
\begin{align*} &\text{A } 2.0~\text{kg block is given a single impulsive force in the positive } x\text{-direction as shown in Fig.~3.} \\ &\text{If the velocity of the block at } t = 0 \text{ was } -2.0~\text{m/s, find its velocity at } t = 5.0~\text{s.} \\[6pt] \end{align*}

\begin{align*} &m = 2.0~\text{kg}, \quad v_0 = -2.0~\text{m/s}. \\[6pt] &\\[-4pt] &\text{From the force-time graph, the impulse is equal to the area under the curve:} \\[4pt] &J = \tfrac{1}{2} \times (5.0~\text{s}) \times (4.0~\text{N}) = 10~\text{N.s}. \\[6pt] &\\[-4pt] &\text{Impulse-momentum theorem:} \\[4pt] &J = m(v - v_0) \\[6pt] &\Rightarrow v = v_0 + \frac{J}{m} \\[6pt] &= (-2.0) + \frac{10}{2.0} \\[6pt] &= (-2.0) + 5.0 \\[6pt] &= 3.0~\text{m/s}. \\[6pt] \end{align*}

\begin{align*} &\text{A } 6.0~\text{kg body moving with velocity } v \text{ breaks up (explodes) into two equal masses.} \\ &\text{One mass travels east at } 3.0~\text{m/s and the other mass travels north at } 2.0~\text{m/s.} \\ &\text{The speed } v \text{ of the } 6.0~\text{kg mass is:} \\ &\\ &\text{A) } 3.0~\text{m/s} \quad\\ &\text{B) } 5.0~\text{m/s} \quad\\ &\text{C) } 1.0~\text{m/s} \quad\\ &\text{D) } 2.0~\text{m/s} \quad\\ &\text{E) } 1.8~\text{m/s} \end{align*}

\begin{align*} &\text{A } 10~\text{kg bomb initially at rest explodes, breaking into two pieces of masses } 4.0~\text{kg and } 6.0~\text{kg.} \\ &\text{The } 4.0~\text{kg piece flies off along the } +x \text{ axis with a speed of } 30~\text{m/s.}\\ &\text{Find the velocity of the } 6.0~\text{kg piece.} \\ &\\ &\text{A) } 20~\text{m/s along the } -x \text{ axis} \quad\\ &\text{B) } 30~\text{m/s along the } -x \text{ axis} \quad\\ &\text{C) } 30~\text{m/s along the } +x \text{ axis} \quad\\ &\text{D) } 20~\text{m/s along the } +x \text{ axis} \quad\\ &\text{E) } 15~\text{m/s along the } -x \text{ axis} \end{align*}

\begin{align*} &\text{As shown in Fig.~4, a ball of mass } M \text{ is hanging from a rope to make a pendulum.} \\ &\text{A } 10~\text{g bullet strikes the ball with a speed } v = 308~\text{m/s. The center of mass of the ball + bullet} \\ &\text{rises a vertical distance of } h = 12~\text{cm.}\\ &\text{Assuming that the bullet remains embedded, calculate the mass } M \text{ of the ball.} \\ &\\ &\text{A) } 8.0~\text{kg} \quad\\ &\text{B) } 5.0~\text{kg} \quad\\ &\text{C) } 3.0~\text{kg} \quad\\ &\text{D) } 6.0~\text{kg} \quad\\ &\text{E) } 2.0~\text{kg} \end{align*}

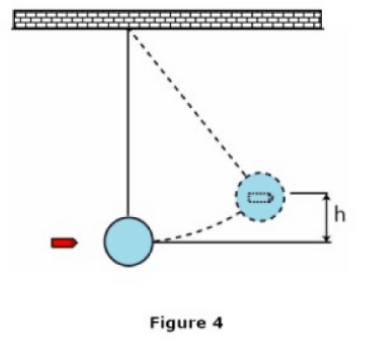
\begin{align*} &\text{As shown in Fig.~4, a ball of mass } M \text{ is hanging from a rope to make a pendulum.} \\ &\text{A } 10~\text{g bullet strikes the ball with a speed } v = 308~\text{m/s. The center of mass of the ball + bullet} \\ &\text{rises a vertical distance of } h = 12~\text{cm.}\\ &\text{Assuming that the bullet remains embedded, calculate the mass } M \text{ of the ball.} \\ \end{align*}

\begin{align*} &\text{Horizontal momentum is conserved in the brief impact:}\\ &\\ &m_b v=\left(M+m_b\right) V .\\ &\\ &\text{Solve for $M$ :}\\ &\\ & M=\frac{m_b v}{V}-m_b \end{align*}

\begin{align*} &\text{kinetic energy (of the combined masses) converts to gravitational potential at the peak}\\ &\frac{1}{2}\left(M+m_b\right) V^2=\left(M+m_b\right) g h \quad \Rightarrow \quad V^2=2 g h\\ &\text{so,} V=\sqrt{2 g h}=\sqrt{2(9.8)(0.12)} \approx 1.53 \mathrm{~m} / \mathrm{s} . \end{align*}

M=\frac{m_b v}{V}-m_b=\frac{0.01\times 308}{1.53}-0.01\approx 2.0\mathrm{~kg}

\begin{align*} &\text{A } 10~\text{gram bullet is shot in the } +x\text{-direction with a speed of } v_0 = 500~\text{m/s} \text{ into a stationary}\\ &\text{block of woodthat has a mass of } 5.0~\text{kg (see Fig.~3). The bullet embeds itself in the block.}\\ &\text{What distance } (d) \text{ will the block slide} \text{ on a surface having a coefficient of kinetic friction}\\ &\text{equal to } 0.5? \\ &\\ &\text{A) } 2~\text{cm} \quad\\ &\text{B) } 50~\text{cm} \quad\\ &\text{C) } 100~\text{cm} \quad\\ &\text{D) } 5~\text{cm} \quad\\ &\text{E) } 10~\text{cm} \end{align*}

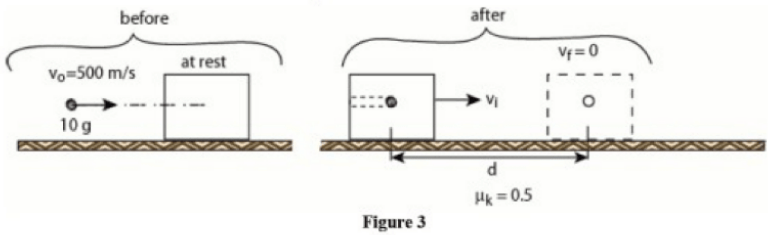
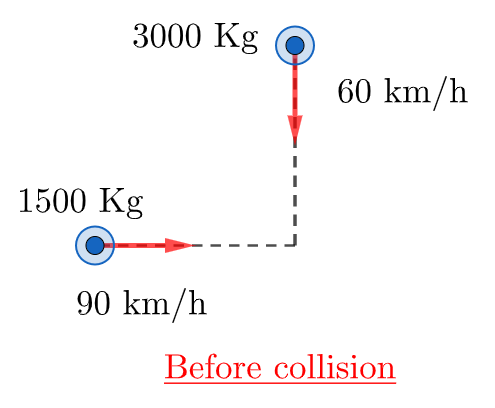
\begin{align*} &\text{A } 1500~\text{kg car traveling at } 90.0~\text{km/h east collides with a } 3000~\text{kg car traveling at } 60.0~\text{km/h } \nonumber \\ &\text{south. The two cars stick together after the collision (see Fig.~2).}\\ &\text{What is the speed of the cars after collision?} \nonumber \\ &\\ &\text{A) } 17.4~\text{m/s} \quad\\ &\text{B) } 8.33~\text{m/s} \quad\\ &\text{C) } 13.9~\text{m/s} \quad\\ &\text{D) } 21.7~\text{m/s} \quad\\ &\text{E) } 50.0~\text{m/s} \nonumber \end{align*}

\text{What is the y-coordinate of the center of mass for the uniform plate shown in Figure 4 }\\ \text{if $L=5.0 \mathrm{~cm}$ ?}

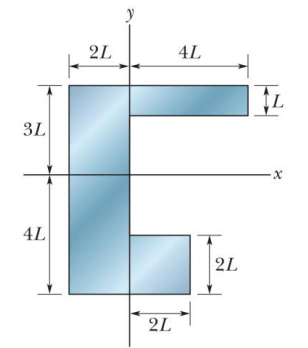
\begin{align*} &\text{A) -2.0 cm }\\ &\text{B) -1.0 cm }\\ &\text{C) +1.0 cm}\\ &\text{D) +2.0 cm}\\ &\text{E) +3.0 cm}\\ \end{align*}