COMP3010: Algorithm Theory and Design

Daniel Sutantyo, Department of Computing, Macquarie University

11.2 - Reduction

Where Are We Now?

11.2 - Reduction

\(\text{EXP}\)

\(\text{P}\)

\(\text{NP}\)

\(\text{EXP}\)

\(\text{NP-hard}\)

\(\text{NP-complete}\)

Where Are We Now

11.2 - Reduction

  • NP-complete decision problems:
    • NP-hard  : any problem in NP can be reduced to it
    • NP            : we can verify if a solution is correct in P time
  • Reduction
    • converting one problem into another problem
    • if I have two problems, A and B, and I can convert from A to B, and I can solve B,  then:
      1. I can solve A using B
      2. I can argue that B is as hard as A

Reduction

11.2 - Reduction

Input for Problem A

Input for Problem B

Solution for Problem B

Solution for Problem A

REDUCER

REDUCER

SOLVER for B

Reduction (Decision Problem)

11.2 - Reduction

Input for Problem A

REDUCER

Input for Problem B

SOLVER for B

Yes / No

Point 1: I Can Solve A using B

11.2 - Reduction

  • NP-complete problems are the most important class for proving or disproving P = NP because every problem in NP can be reduced to a problem in NP-complete
  • So if just one problem in NP-complete can be done in polynomial time, that means we can solve every problem in NP in polynomial time, thus P = NP
  • Wait, isn't that just reducing an NP-complete problem to a polynomial-time algorithm?

Point 1: I Can Solve A using B

11.2 - Reduction

  • Travelling Salesman (decision problem):
    • Given a list of cities and the distance between any pair of cities, is there a route that visits each city exactly once and returns to the origin city, of length at most \(L\)
  • Why not just get all the possible cycles that goes through every city, put that inside an array, then REDUCE it to a linear search problem (find the cycle with the least distance)

Point 1: I Can Solve A using B

11.2 - Reduction

  • Why not just get all the possible cycles from the starting city that goes through every other city once, put that inside an array, then REDUCE it to a linear search problem (find the cycle with the least distance)
  • No, because making the array that contains all the possible cycles needs to be done in exponential time!

Travelling

Salesman

Linear
Search

REDUCER

Polynomial-Time Reduction Algorithm

11.2 - Reduction

  • If we reduce an NP problem to a polynomial-time problem, but the reduction algorithm is exponential, then that means we need exponential time to solve it anyway
    • not useful because we want so solve problems in polynomial time
  • Similarly, if we convert an NP problem to an NP-complete problem, but the reduction algorithm is exponential, then even if we can solve the NP-complete problem in polynomial time, this won't mean much
  • Therefore the reduction that we have mentioned earlier MUST BE doable in polynomial time
    • a problem H is NP-hard if every problem L in NP can be reduced in polynomial time to H

Polynomial-Time Reduction Algorithm

11.2 - Reduction

  • Remember how we can use the decision problem algorithm to solve the optimisation problem algorithm?

What is the length of the shortest route in the TSP problem

Is there a cycle of length k?

REDUCER

for k = 0 to MAX

Length of the shortest route in the TSP problem

Where Are We Now

11.2 - Reduction

  • Reduction
    • if I have algorithms for two problems, A and B, I can convert from A to B, and I can solve B,  then:​
      1. I can solve A using B
      2. I can argue that B is as hard as A
    • ​the reduction algorithm must be polynomial in complexity

Point 2: I Can Argue that B is as Hard as A

11.2 - Reduction

  • The point of doing reduction, believe it or not, is not to actually try to solve NP problems
    • we reduce NP-complete problems to NP problems so that if we solve any of the NP-complete problem, then we can say that P = NP
    • how likely is this to happen?
  • So why even bother talking about reduction?
    • because reduction is a way for us to say that a problem is HARD

Point 2: I Can Argue that B is as Hard as A

11.2 - Reduction

because reduction is a way for us to say that a problem is HARD

because reduction is a way for us to say that a problem is HARD

Point 2: I Can Argue that B is as Hard as A

11.2 - Reduction

Illustration by Stefan Szeider, https://www.ac.tuwien.ac.at/people/szeider/cartoon/

Notation

11.2 - Reduction

  • If Problem A can be reduced in polynomial time to Problem B, then we write

A \(\le_p\) B

  • If you can reduce Problem A to Problem B, which one do you think is harder?
    • my favourite memory aid for this is the searching (findMax) versus sorting story from COMP125
      • I can use the sorting algorithm to perform findMax
      • I need to muck around with findMax to make it sort
      • so sorting is harder, or it is at least as hard as findMax

Notation

11.2 - Reduction

  • If Problem A can be reduced in polynomial time to Problem B, then we write

A \(\le_p\) B \(x^2+x+1\)

  • The notation has the correct mnemonic because B is at least as hard as A
     
  • There is a formal proof for this, but I hope it is intuitive because we are actually saying that if you can solve B, you can solve A
    • if you can solve A, can you solve B?
    • can they be of the same difficulty?

Which One is Harder?

11.2 - Reduction

  • Let's look at all possibilities
    • for now, you can think that 'easy' is P, and 'hard' is NP (or EXP)

A \(\le_p\) B

A is easy, B is hard

Can you solve an easy problem in a hard way? Yes! 

(cue in the poor COMP125 student)

  • Can I reduce A to B?

11.2 - Reduction

A is easy, B is hard

A \(\le_p\) B

  • Can I reduce A to B?

Which One is Harder?

11.2 - Reduction

You shouldn't be able to do that (this is trying to do Travelling Salesman Problem using linear search)

A is easy, B is hard

A \(\le_p\) B

  • Can I reduce A to B?

A is hard, B is easy

Which One is Harder?

11.2 - Reduction

A is easy, B is hard

A \(\le_p\) B

  • Can I reduce A to B?

A is hard, B is easy

Which One is Harder?

11.2 - Reduction

A is easy, B is hard

A \(\le_p\) B

  • Can I reduce A to B?

A is hard, B is easy

Which One is Harder?

A is easy, B is easy

A is hard, B is hard

11.2 - Reduction

A is easy, B is hard

A \(\le_p\) B

  • Can I reduce A to B?

A is hard, B is easy

Which One is Harder?

A is easy, B is easy

A is hard, B is hard

These are fine, but not very useful, it just says that we can convert P problems to P problems and NP problems to NP problems (we stay in the complexity class)

11.2 - Reduction

A is easy, B is hard

A \(\le_p\) B

  • Can I reduce A to B?

A is hard, B is easy

Which One is Harder?

A is easy, B is easy

A is hard, B is hard

11.2 - Reduction

A is easy, B is hard

A \(\le_p\) B

A is hard, B is easy

Which One is Harder?

A is easy, B is easy

A is hard, B is hard

  • Now here's the question: if A \(\le_p\) B, and B is easy, what does this mean?
    • it means that A must be easy as well
    • if A is NP-complete, and we can reduce it in polynomial time to a problem B which is polynomial, then we have shown that A is in P as well
      • this is what we talked about earlier, but again, this is not our main point

11.2 - Reduction

A is easy, B is hard

A \(\le_p\) B

A is hard, B is easy

Which One is Harder?

A is easy, B is easy

A is hard, B is hard

  • Our main question is this: if A \(\le_p\) B, and A is hard, what does this mean?
    • B cannot be easy
    • so if A is NP-complete then B must be ... ?

11.2 - Reduction

A is easy, B is hard

A \(\le_p\) B

A is hard, B is easy

Which One is Harder?

A is easy, B is easy

A is hard, B is hard

  • Our main question is this: if A \(\le_p\) B, and A is hard, what does this mean?
    • B cannot be easy
    • so if A is NP-complete then B must be NP-Hard
      • well actually, if A is NP-hard then so is B, because every NP problem can be reduced to A, and we can reduce A to B
      • whether or not B is NP-complete depends if B is in NP

11.2 - Reduction

Using Reduction

  • So, the way we use the reduction A \(\le_p\) B is not to ask if B is in P, because we're not trying to show that A is in P (at least not in this unit)
  • We use the reduction A \(\le_p\) B to show that B is hard, i.e. B is NP-hard

A is easy, B is hard

A is hard, B is easy

A is easy, B is easy

A is hard, B is hard

  • Here is the scenario:
    • we are given a problem B, and we don't know if it's NP-hard or not
    • we pick a problem A that we know is NP-complete
    • we reduce A to B
    • we have shown that B is NP-hard
    • if we can show that B is NP, then we know B is NP-complete

11.2 - Reduction

Using Reduction

  • Here is the scenario:
    • we are given a problem B, and we don't know if it's NP-hard or not
    • we pick a problem A that we know is NP-complete
    • we reduce A to B
    • we have shown that B is NP-hard
    • if we can show that B is NP, then we know B is NP-complete
  • Remember the direction of the reduction, you are reducing from a problem that you already know to the problem that you don't know

A

B

\(\le_p\)

(known)

(unknown)

NP-hard

NP-complete

11.2 - Reduction

Using Reduction

  • This is the system that was used to establish the problems that we now know are in NP-complete
    • they start with a known NP-complete problem, and then keeps reducing it to other problems
    • but that means there must be the original NP-complete problem, right?  the first one

(disclaimer: I never saw Twilight)

11.2 - Reduction

Cook-Levin's Theorem

  • The first NP-complete problem is the boolean satisfiability problem (or circuit satisfiability problem)

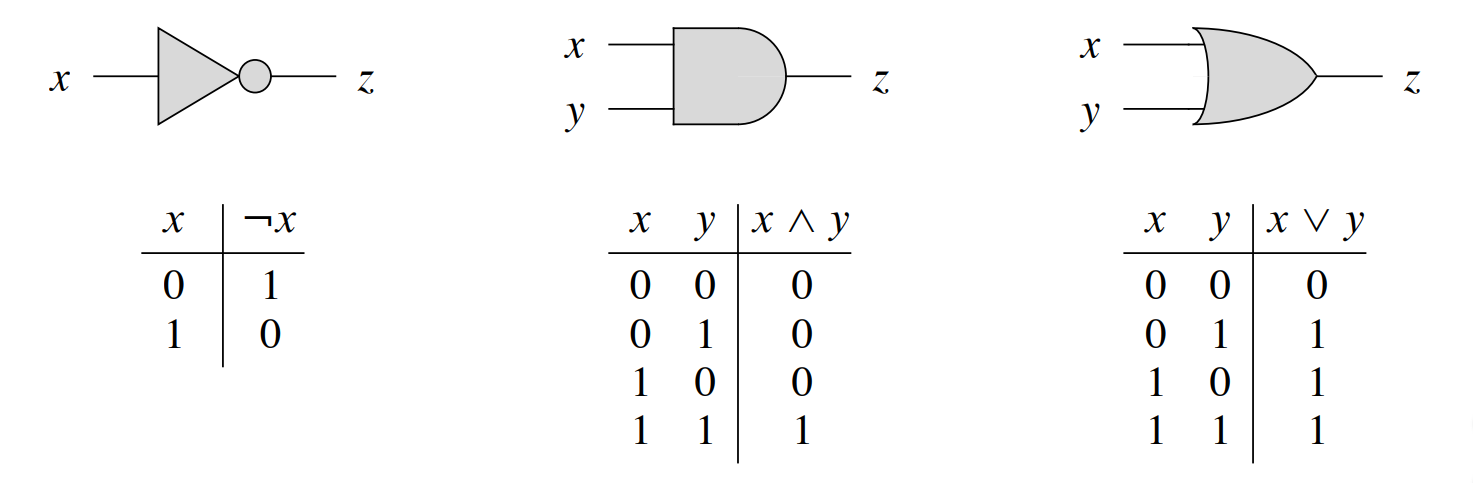
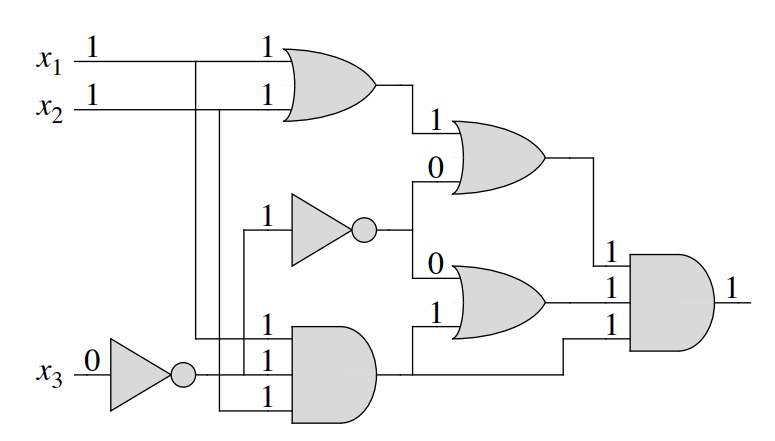
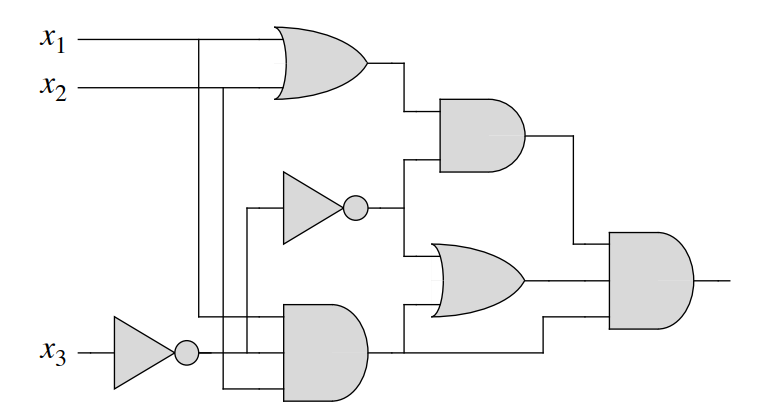
11.2 - Reduction

Cook-Levin's Theorem

  • The first NP-complete problem is the boolean satisfiability problem (or circuit satisfiability problem)

\[x_0 \lor \neg x_1  \lor \neg x_3  \]

\[x_1 \lor x_2 \lor \neg x_3  \]

\[\neg x_0 \lor \neg x_2 \lor x_3  \]

\[x_0 \lor x_1 \lor  x_3  \]

11.2 - Reduction

Cook-Levin's Theorem

  • The first NP-complete problem is the boolean satisfiability problem (or circuit satisfiability problem)

\[x_0 \lor \neg x_1  \lor \neg x_3  \]

\[x_1 \lor x_2 \lor \neg x_3  \]

\[\neg x_0 \lor \neg x_2 \lor x_3  \]

\[x_0 \lor x_1 \lor  x_3  \]

\[x_0 = 1, x_1 = 1, x_2 = 1, x_3 = 1\]

1            0             0 

1         1           0 

0           0          1 

1          1          1 

11.2 - Reduction

Cook-Levin's Theorem

  • The first NP-complete problem is the boolean satisfiability problem (or circuit satisfiability problem)
  • The proof is beyond the scope for this unit, and it is even beyond the scope of CLRS
    • SAT is what we call the mother problem, the first NP-complete problem that can be reduced to other NP-complete problems

11.2 - Reduction

NP-Complete Reduction Hierarchy

SAT

3-SAT or 3-CNF 

Clique

Vertex Cover

Hamiltonian Cycle

Travelling Salesman

Subset Sum

Partition

Knapsack

11.2 - Reduction

NP-Complete Reduction Hierarchy

SAT

3-SAT or 3-CNF 

Clique

Vertex Cover

Hamiltonian Cycle

Travelling Salesman

Subset Sum

Partition

Knapsack

Your
Problem

Summary

11.2 - Reduction

  • Reduction must be done in polynomial-time
  • A \(\le_p\) B
    • if we know that A is NP-complete
      • if B is in P, then we have proven P = NP
    • if we don't know about B:
      • if A is NP-complete, then B must be NP-hard (by definition)
  • Make sure you understand the direction of the reduction
  • Are we going to do any reduction?

COMP3010 - 11.2 - Reduction

By Daniel Sutantyo

COMP3010 - 11.2 - Reduction

  • 180

More from Daniel Sutantyo