COMP3010: Algorithm Theory and Design
Daniel Sutantyo, Department of Computing, Macquarie University
4.1 - Optimal Substructure
4.1 - Optimal Substructure
Divide and Conquer
- We are going to discuss divide-and-conquer some more in Week 6, but you are already very familiar with it (I hope ...)
- Divide the problem into smaller subproblems
- Conquer the subproblems
- Combine the solutions to the subproblem into the solution for the original problem (sometimes this is optional)
- Classical example: mergesort
- Note that you are using the same algorithm to compute the subproblems, so it's like starting fresh with a different set of inputs
4.1 - Optimal Substructure
Divide and Conquer
- Questions:
- is recursive fibonacci algorithm a divide-and-conquer algorithm?
- is binary search a divide-and-conquer algorithm?
- is finding largest element a divide-and-conquer algorithm?
- is recursive fibonacci algorithm a divide-and-conquer algorithm?
public static int fib(int n) {
if (n <= 2)
return 1;
else return fib(n-1) + fib(n-2);
}4.1 - Optimal Substructure
Divide and Conquer
fib(n)
fib(n-1)
fib(n-2)
find_largest(0,n)
find_largest(0,0)
find_largest(1,n)
binary_search(0,n)
binary_search(0,n/2)
binary_search(n/2+1,n)
4.1 - Optimal Substructure
Divide and Conquer
binary_search(0,n)
binary_search(0,n/2)
binary_search(n/2+1,n)
(p.s. I have seen discard and conquer)
4.1 - Optimal Substructure
Divide and Conquer
find_largest(0,n)
find_largest(0,0)
find_largest(1,n)
4.1 - Optimal Substructure
Divide and Conquer
public static int find_largest(int[] a, int i, int j, int max) {
if(i > j)
return -1;
if(a[i] > max)
max = a[i];
return Math.max(max, find_largest(a,i+1,j,max));
}public static int find_largest(int[] a, int i, int j, int max) {
if(i > j)
return -1;
int m = (i+j)/2;
if(a[m] > max)
max = a[m];
return Math.max(max,Math.max(find_largest(a,i,m-1,max), find_largest(a,i+1,j,max)));
}4.1 - Optimal Substructure
Divide and Conquer
public static int find_largest(int[] a, int i, int j, int max) {
if(i > j)
return -1;
int m = (i+j)/2;
if(a[m] > max)
max = a[m];
return Math.max(max,Math.max(find_largest(a,i,m-1,max), find_largest(a,i+1,j,max)));
}find_largest(0,n)
find_largest(0,n/2)
find_largest(n/2+1,n)
4.1 - Optimal Substructure
Divide and Conquer
fib(n)
fib(n-1)
fib(n-2)
binary_search(0,n)
binary_search(0,n/2)
binary_search(n/2+1,n)
- Why are we discussing this?
- in which problem(s) can you apply dynamic programming
find_largest(0,n)
find_largest(0,n/2)
find_largest(n/2+1,n)
4.1 - Optimal Substructure
Dynamic Programming and Divide and Conquer

dynamic
programming
divide and
conquer
- Dynamic programming is a divide and conquer approach
- However, it doesn't mean we can apply it on every problem
- we mostly use DP for optimisation problems
- we don't use it as much with search problems (but can we?)
- decision problem?
- counting problem?
4.1 - Optimal Substructure
Dynamic Programming and Divide and Conquer
- Knapsack problem: given a set of items, each with weight and value, and a limit L, work out which items we should take so that the value is maximised with total weight less than L
- Can you use dynamic programming to solve knapsack?
4.1 - Optimal Substructure
Knapsack
| A | B | C | D | E | F | G | H | |
|---|---|---|---|---|---|---|---|---|
| weight | 7 | 5 | 12 | 5 | 6 | 4 | 8 | 11 |
| value | $12 | $9 | $18 | $9 | $12 | $5 | $15 | $21 |
[ A ]
L = 33
V = 12
L (Limit) = 40
L = 40
V = 0
[ ]
pick A
[ ]
pick B
pick B
[ A B ]
L = 28
V = 21
[ A ]
L = 33
V = 12
[ B ]
L = 35
V = 9
[ ]
L = 40
V = 0
L = 40
V = 0
pick C
pick C
pick C
don't pick C
pick C
[ A B C ]
L = 16
V = 39
[ A B ]
L = 28
V = 21
[ A C ]
L = 21
V = 30
[ A ]
L = 33
V = 12
[ B C ]
L = 23
V = 27
[ B ]
L = 35
V = 9
[ C ]
L = 28
V = 18
[ ]
L = 40
V = 0
don't pick C
don't pick C
don't pick C
don't pick B
don't pick B
don't pick A
4.1 - Optimal Substructure
Knapsack
- Is dynamic programming only good for optimisation problem?
- Decision problem?
- Is there a value > V with weight under the limit L?
- Search problem?
- Give all the combinations with value > V and weight under limit L
- Counting problem?
- How many combinations are there with value > V and weight under limit L
4.1 - Optimal Substructure
Optimal Substructure
- Majority of the material is taken from CLRS Chapter 15
- So far we know that we can use dynamic programming as long as the problem has overlapping subproblems
- However, there is another important criteria, the problem must exhibits optimal substructure:
A problem exhibits optimal substructure if the optimal solution to the problem can be constructed using optimal solutions to the subproblems
4.1 - Optimal Substructure
Optimal Substructure
A problem exhibits optimal substructure if the optimal solution to the problem can be constructed using optimal solutions to the subproblems
- Obviously this statement only applies for optimisation problems, but the basis of this statement is just what divide and conquer is
- we use the solution to the subproblems to construct the solution to the problem
fib(n)
fib(n-1)
fib(n-2)
find_largest(0,n)
find_largest(0,n/2)
find_largest(n/2+1,n)
4.1 - Optimal Substructure
Knapsack
| A | B | C | D | E | F | G | H | |
|---|---|---|---|---|---|---|---|---|
| weight | 7 | 5 | 12 | 5 | 6 | 4 | 8 | 11 |
| value | $12 | $9 | $18 | $9 | $12 | $5 | $15 | $21 |
[ A ]
L = 33
V = 12
L (Limit) = 40
L = 40
V = 0
[ ]
pick A
[ ]
pick B
pick B
[ A B ]
L = 28
V = 21
[ A ]
L = 33
V = 12
[ B ]
L = 35
V = 9
[ ]
L = 40
V = 0
L = 40
V = 0
pick C
pick C
pick C
don't pick C
pick C
[ A B C ]
L = 16
V = 39
[ A B ]
L = 28
V = 21
[ A C ]
L = 21
V = 30
[ A ]
L = 33
V = 12
[ B C ]
L = 23
V = 27
[ B ]
L = 35
V = 9
[ C ]
L = 28
V = 18
[ ]
L = 40
V = 0
don't pick C
don't pick C
don't pick C
don't pick B
don't pick B
don't pick A
4.1 - Optimal Substructure
Knapsack
| A | B | C | D | E | F | G | H | |
|---|---|---|---|---|---|---|---|---|
| weight | 7 | 5 | 12 | 5 | 6 | 4 | 8 | 11 |
| value | $12 | $9 | $18 | $9 | $12 | $5 | $15 | $21 |
[ A ]
L = 33
V = 12
L (Limit) = 40
L = 40
V = 0
[ ]
pick A
[ ]
pick B
pick B
L = 40
V = 0
pick C
pick C
pick C
don't pick C
pick C
[ A B C ]
L = 16
V = 39
[ A B ]
L = 28
V = 21
[ A C ]
L = 21
V = 30
[ A ]
L = 33
V = 12
[ B C ]
L = 23
V = 27
[ B ]
L = 35
V = 9
[ C ]
L = 28
V = 18
[ ]
L = 40
V = 0
don't pick C
don't pick C
don't pick C
don't pick B
don't pick B
don't pick A
4.1 - Optimal Substructure
Knapsack
| A | B | C | D | E | F | G | H | |
|---|---|---|---|---|---|---|---|---|
| weight | 7 | 5 | 12 | 5 | 6 | 4 | 8 | 11 |
| value | $12 | $9 | $18 | $9 | $12 | $5 | $15 | $21 |
L (Limit) = 40
L = 40
V = 0
[ ]
pick A
pick B
pick B
pick C
pick C
pick C
don't pick C
pick C
[ A B C ]
L = 16
V = 39
[ A B ]
L = 28
V = 21
[ A C ]
L = 21
V = 30
[ A ]
L = 33
V = 12
[ B C ]
L = 23
V = 27
[ B ]
L = 35
V = 9
[ C ]
L = 28
V = 18
[ ]
L = 40
V = 0
don't pick C
don't pick C
don't pick C
don't pick B
don't pick B
don't pick A
4.1 - Optimal Substructure
Knapsack
| A | B | C | D | E | F | G | H | |
|---|---|---|---|---|---|---|---|---|
| weight | 7 | 5 | 12 | 5 | 6 | 4 | 8 | 11 |
| value | $12 | $9 | $18 | $9 | $12 | $5 | $15 | $21 |
L (Limit) = 40
pick A
pick B
pick B
pick C
pick C
pick C
don't pick C
pick C
[ A B C ]
L = 16
V = 39
[ A B ]
L = 28
V = 21
[ A C ]
L = 21
V = 30
[ A ]
L = 33
V = 12
[ B C ]
L = 23
V = 27
[ B ]
L = 35
V = 9
[ C ]
L = 28
V = 18
[ ]
L = 40
V = 0
don't pick C
don't pick C
don't pick C
don't pick B
don't pick B
don't pick A
4.1 - Optimal Substructure
Optimal Substructure
What is the optimal answer to the problem
171
Subproblem B
Subproblem C
Subproblem D
43
Subproblem A
89
4.1 - Optimal Substructure
Optimal Substructure
What is the optimal answer to the problem
171
43
89
152
193
23
4.1 - Optimal Substructure
Optimal Substructure
What is the optimal answer to the problem
171
43
89
152
193
23
4.1 - Optimal Substructure
Optimal Substructure
- Exercise: Do these problems have optimal substructure property?
- Minimum spanning tree
- Shortest path
- What about harder problems?
- Minimum vertex cover?
- Travelling salesman?
4.1 - Optimal Substructure
Optimal Substructure - Shortest Path
- Shortest path: find the shortest path from the starting node to every other node
Z
B
A
C
X
Y
???
4.1 - Optimal Substructure
Optimal Substructure
- Travelling salesman: find the shortest route to visit every city and then return to the origin city
- Let \(A\) be the starting city
- Problem: \(A \rightarrow \text{(every other city)} \rightarrow A\)
- Subproblem:
- \(A \rightarrow B\)
- \(B \rightarrow \text{(every other city)} \rightarrow A\)
- Does this mean you can use dynamic programming to solve the travelling salesman problem?
4.1 - Optimal Substructure
Optimal Substructure
- Does this mean you can use dynamic programming to solve the travelling salesman problem?
- Does this mean you can use dynamic programming to solve the travelling salesman problem EFFICIENTLY?
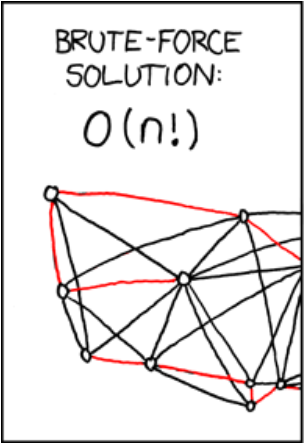


4.1 - Optimal Substructure
Optimal Substructure
- Huge majority (if not all) of the problems that you have encountered so far would have this optimal substructure property
- If we don't have this property, then why bother breaking it down into smaller and smaller subproblems
- Why do we care if the problem has optimal substructure property?
- we want to find optimal solution to the problem
- we break down our problems to smaller subproblems (because it is easier to do smaller problems, and we can find overlaps)
- we want to apply the same algorithm to the subproblem, i.e. we also want to find the optimal solution to that subproblem
4.1 - Optimal Substructure
Optimal Substructure
- However, not every problem has optimal substructure, so you need to be careful
- in other words, with these problems, when we apply the same algorithm to the subproblem, it does give an optimal solution BUT this doesn't help in giving an optimal solution to the original problem
- do we still break them down?
- yes, but often just to find all the possible combinations (brute force), it's hard to give a generalised answer here, it really depends on the problem
4.1 - Optimal Substructure
Problems without Optimal Substructure
- Longest path problem
- find the longest path between two vertices without visiting any vertices twice (i.e. a simple path)
A
C
B
E
D
4.1 - Optimal Substructure
Problems without Optimal Substructure
- Longest path problem
- if we want to find the longest path from A to E, then one possible decomposition is for to find the longest path from A to B and from B to E
- what is the longest path from B to E though?
A
C
B
E
D
A
B
A
B
A
B
A
C
B
E
D
A
B
A
B
A
B
4.1 - Optimal Substructure
Problems without Optimal Substructure
- Longest path problem
- if we want to find the longest path from A to E, then one possible decomposition is for to find the longest path from A to B and from B to E
- what is the longest path from B to E though?
A
C
B
E
D
A
B
A
B
A
B
A
C
B
E
D
A
B
A
B
A
B
longest path from A to B
longest path from B to E
4.1 - Optimal Substructure
Problems without Optimal Substructure
- Longest path problem
- you can probably 'fix' this by changing the definition of the problem, e.g. find the longest path that doesn't use the vertices in a set
- but hopefully you can see why we need to define the problem properly
A
C
B
E
D
A
B
A
B
A
B
A
C
B
E
D
A
B
A
B
A
B
longest path from A to B
longest path from B to E
4.1 - Optimal Substructure
Problems without Optimal Substructure
- Maximum clique problem
- a clique is a set of vertices, all adjacent to each other
- find the clique with the largest number of vertices
- what is the subproblem?
4.1 - Optimal Substructure
Problems without Optimal Substructure
- Maximum clique problem
- a clique is a set of vertices, all adjacent to each other
- find the clique with the largest number of vertices
- what is the subproblem?
4.1 - Optimal Substructure
Summary
- Optimal substructure
- what it is
- why do you need it
- does every problem have it?
COMP3010 - 4.1 - Optimal Substructure
By Daniel Sutantyo
COMP3010 - 4.1 - Optimal Substructure
Understanding optimal substructure
- 291



