COMP3010: Algorithm Theory and Design
Daniel Sutantyo, Department of Computing, Macquarie University
7.2 - Huffman Coding
Motivation
- Each character is in a text file is 1 byte (8-bit ASCII value)
- So, if we have a text file with 1000 characters, then it should be 1000 bytes in size.
- can we do better?
- great explanation here: https://www.youtube.com/watch?v=JsTptu56GM8
7.2 - Huffman Coding
Motivation
7.2 - Huffman Coding
Motivation
7.2 - Huffman Coding
Motivation


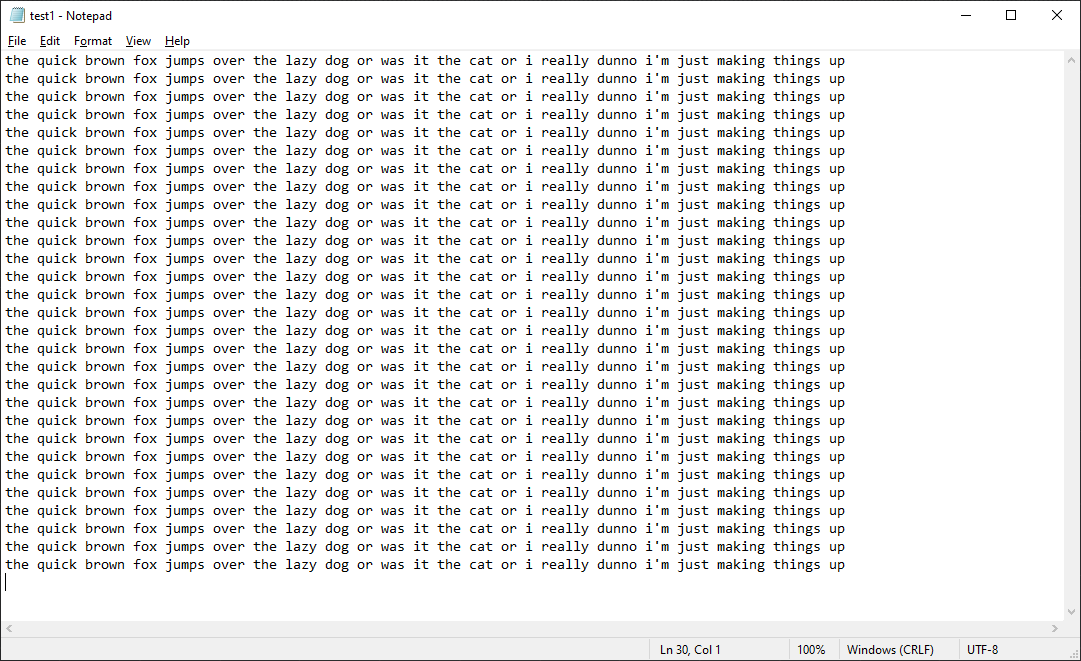
test1:
3,103 bytes to 262 bytes
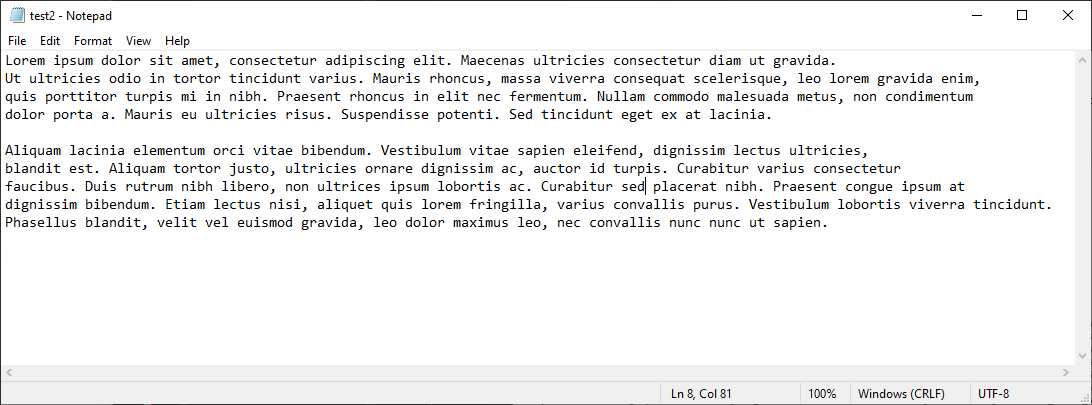
test2:
1,042 bytes to 665 bytes
7.2 - Huffman Coding
How can we do this?
- Each character is in a text file is 1 byte (8-bit ASCII value)
- However, 1 byte can be used to represent 256 different characters, and in English, we simply don't have that many characters,
- even after accounting for capitalisation, numbers, and other symbols (? , #, @, etc), see the ASCII table
- plus, do we use all the characters when we write a text document (~, <, > )
- How about if we use variable length code instead?
7.2 - Huffman Coding
How can we do this?
- We really don't have that many characters here, so why don't we use a shorter representation for 'e' (because it occurs a lot)
- For example, we can use '1' to represent 'e', just one bit!
- of course we have to be careful, because if we use '11' to represent 's', then how can we differentiate between "ss" and "eeee"?
"The assignment is due next week. Reeeeeeeeeeeeeeeeeeeeeeeeeeeee"
- anonymous student
7.2 - Huffman Coding
Prefix codes
- We need to use what is known as prefix codes:
- prefix codes is what we call codes where none of the code word is a prefix of another code word
- for example, if we choose to represent 'e' with 1, then we cannot have 10, 11, 100, etc, because those starts with 1
- as an example, consider the following codes:
- 01 : a 001 : i 0001 : d 0000 : k 11 : e 10 : s
- we use shorter representations for characters that occur many times in the document
7.2 - Huffman Coding
Prefix codes
- Binary prefix codes can be represented nicely using a binary tree
- 01 : a 001 : i 0001 : d 0000 : k 11 : e 10 : s
- Decoding is easy:
- 0: go left
- 1: go right
- stop at leaves
i
d
k
a
s
e
7.2 - Huffman Coding
Huffman Coding
7.2 - Huffman Coding
- In 1952, Huffman invented a greedy algorithm to produce an optimal prefix code for data compression
- The algorithm is quite simple:
- create a single-node tree (leaf) for each character in the document and assign their frequencies as the weight for the node
- put all the node in a priority queue, least weight on top
- pop two trees from the priority queue, then join them together (making a new root) and then put them back in the priority queue, using their combined weights as the weight
- proceed until there is only one tree in the priority queue
Huffman Coding
7.2 - Huffman Coding
- Example:
- a : 4 c : 2 e : 9 f : 1 h : 2 j : 1 m : 2 s : 6 w : 1
a
c
e
f
h
j
m
s
w
4
2
9
1
2
1
2
6
1
Huffman Coding
7.2 - Huffman Coding
a
c
e
f
h
j
m
s
w
4
2
9
1
2
1
2
6
1
Huffman Coding
7.2 - Huffman Coding
a
c
e
f
h
j
m
s
w
4
2
9
1
2
1
2
6
1
Huffman Coding
7.2 - Huffman Coding
a
c
e
f
h
j
m
s
w
4
2
9
1
2
1
2
6
1
Huffman Coding
7.2 - Huffman Coding
a
c
e
f
h
j
m
s
w
4
2
9
2
2
1
2
6
Huffman Coding
7.2 - Huffman Coding
a
c
e
f
h
j
m
s
w
4
2
9
2
2
1
2
6
Huffman Coding
7.2 - Huffman Coding
a
c
e
f
h
j
m
s
w
4
2
9
2
2
1
2
6
Huffman Coding
7.2 - Huffman Coding
a
c
e
f
h
j
m
s
w
4
2
9
3
2
2
6
Huffman Coding
7.2 - Huffman Coding
a
c
e
f
h
j
m
s
w
4
2
9
3
2
2
6
Huffman Coding
7.2 - Huffman Coding
a
c
e
f
h
j
m
s
w
4
2
9
3
2
2
6
Huffman Coding
7.2 - Huffman Coding
a
c
e
f
h
j
m
s
w
4
9
3
4
2
6
Huffman Coding
7.2 - Huffman Coding
a
c
e
f
h
j
m
s
w
4
9
3
4
2
6
Huffman Coding
7.2 - Huffman Coding
a
c
e
f
h
j
m
s
w
4
9
3
4
2
6
Huffman Coding
7.2 - Huffman Coding
a
c
e
f
h
j
m
s
w
4
9
5
4
6
Huffman Coding
7.2 - Huffman Coding
a
c
e
f
h
j
m
s
w
4
9
5
4
6
Huffman Coding
7.2 - Huffman Coding
a
c
e
f
h
j
m
s
w
9
5
8
6
Huffman Coding
7.2 - Huffman Coding
a
c
e
f
h
j
m
s
w
9
8
11
7.2 - Huffman Coding
a
c
e
f
h
j
m
s
w
11
17
Huffman Coding
7.2 - Huffman Coding
a
c
e
f
h
j
m
s
w
Huffman Coding
7.2 - Huffman Coding
a
c
e
f
h
j
m
s
w
Huffman Coding
- Example:
- a : 4 c : 2 e : 9 f : 1 h : 2 j : 1 m : 2 s : 6 w : 1
7.2 - Huffman Coding
Huffman Coding
- Can we show that this tree is optimal?
- How do we measure it?
- we know the frequency of each character
- the depth of the tree is the length of the code for that character
- so given a tree we know the 'cost' of the tree:
- multiply the frequency of each character with the height of the node containing that character
- How do we measure it?
7.2 - Huffman Coding
Huffman Coding
- We can show that the greedy choice is safe to make
- use proof by contradiction (the standard defense)
- in our construction, we always put the characters with the lowest frequencies at the bottom of the tree (can you show this?)
- let \(x\) and \(y\) be the two characters with the lowest frequencies (they must be siblings)
a
y
x
b
7.2 - Huffman Coding
Huffman Coding
- if the resulting tree is not optimal, then there is an optimal tree where \(x\) and \(y\) are NOT at the lowest level
- suppose we swap \(x\) and \(a\)
- let's suppose \(a\) occurs just one more time than \(x\) and \(a\) is only one level above \(x\) (if both have the same frequencies, then our tree is just as optimal)
a
y
x
b
x
y
a
b
7.2 - Huffman Coding
Huffman Coding
- let \(f(x)\) and \(f(a)\) be the frequencies of \(x\) and \(a\) respectively, and let \(h(x)\) and \(h(a)\) be the height of \(x\) and \(a\)
- if we swap \(x\) and \(a\), we will need less bits to represent \(x\) but more bits to represent \(a\)
- before swap:
- cost of representing \(x\) : \(h(x) * f(x)\)
- cost of representing \(a\) : \(h(a) * f(a) = (h(x) - 1) * (f(x)+1)\)
- after swap (\(h(x)\) refers to the original height of \(x\))
- cost of representing \(x\) : \((h(x)-1) * f(x)\)
- cost of representing \(a\) : \(h(x) * (f(x)+1)\)
- before swap:
7.2 - Huffman Coding
Huffman Coding
- cost before swap:
- \(h(x) * f(x) + (h(x)-1)(f(x)+1) = 2h(x)f(x) - f(x) + h(x)-1 \)
- cost after swap:
- \((h(x)-1)*f(x) + h(x)\left(f(x)+1\right) = 2h(x)f(x) - f(x) + h(x) \)
- difference (after - before) is \(1\)
7.2 - Huffman Coding
Huffman Coding
- if \(f(a) = f(x) + m\) for some \(m \ge 1\) and \(h(a) = h(x) - n\) for some \(n \ge 1\) then
- cost before swap:
- \(h(x) * f(x) + (h(x)-n)(f(x)+m) = 2h(x)f(x) - nf(x) + mh(x)-nm \)
- cost after swap:
- \((h(x)-n)*f(x) + h(x)\left(f(x)+m\right) = 2h(x)f(x) - nf(x) + mh(x) \)
- cost before swap:
- difference (after - before) is \(mn\), always a positive difference
- so it is not possible for the alternative tree to be optimal, since in fact ours is always better
7.2 - Huffman Coding
Huffman Coding
- optimal substructure can also be shown using the usual cut-and-paste algorithm
- we can discuss this during the workshop
- it may also be a good practice for you to write an implementation
OpicsJSON
KondorJSON
OpicsSwagger
Mapper
VRProduct
(decides which field goes where depending on the customer)
Logic
COMP3010 - 7.2 - Huffman Encoding
By Daniel Sutantyo
COMP3010 - 7.2 - Huffman Encoding
- 252



