COMP3010: Algorithm Theory and Design

Daniel Sutantyo, Department of Computing, Macquarie University

9.2 - Randomised Algorithms

Prelude

9.2 - Randomised Algorithms

In the previous lecture, we mentioned that to perform average-case analysis properly, we need to know the distribution of the input data
- we often just assume that the data is uniformly distributed
Sometimes it is not possible to know the distribution of the input data, so we have to make assumptions, which can be faulty
- for example, in the previous lecture we said that the average-case complexity of find max algorithmis \(O(\log n)\) comparison, but what if the input is always an array sorted in ascending order?

Prelude

9.2 - Randomised Algorithms

let M = element 1

for i = 2 to n:
   compare element i with M         // cost is c_c
   if M is less than element i:
      assign i to M                 // cost is c_a

If the input is always in ascending order, then you can do this problem in \(O(1)\)
The problem happens when MOST of the time, the input is in ascending order, making our average-case complexity close to the worst-case complexity
So what can you do?
- sort it?
- randomise it?

Prelude

9.2 - Randomised Algorithms

let M = element 1

for i = 2 to n:
   compare element i with M         // cost is c_c
   if M is less than element i:
      assign i to M                 // cost is c_a

If you randomise the input, then you will end up with a \(O(\log n)\) average-case time complexity
- but how much would this cost?

Fisher-Yates Shuffle

9.2 - Randomised Algorithms

Fisher-Yates shuffle:
- how to generate a random permutation of a finite sequence?
  - Put all the numbers into a hat
  - Draw them out one by one
- complexity is \(O(n)\)
- in practice, we use a pseudorandom-number generator (Java Random or SecureRandom class)

Randomising Input

9.2 - Randomised Algorithms

let M = element 1

for i = 2 to n:
   compare element i with M         // cost is c_c
   if M is less than element i:
      assign i to M                 // cost is c_a

Randomising the input in the case of linear search is not worth it, because it will cost another \(O(n)\) operations
However, for problems with a worse time-complexity, it may be worthwhile to randomise your input, that is, to introduce randomness to your algorithm

Probabilistic Analysis vs Randomised Algorithms

9.2 - Randomised Algorithms

Probabilistic analysis:
- we use probabilistic analysis to work out the average-case running time of a deterministic algorithm
  - i.e. if you use the same input, it will always give the same output, with the exact same steps
Randomised algorithm (or probabilistic algorithm):
- a randomised algorithm incorporates some randomness in its execution, so given the same inputs, you may produce different outputs (or the same output but with different steps)
- you can derive the expected running time without knowing the distribution of the input (because you randomise the input)

Probabilistic Analysis vs Randomised Algorithms

9.2 - Randomised Algorithms

With probabilistic analysis, if there is only one input, then we cannot say much about the average running time of our algorithm because we do not know the distribution of our input data
- we also cannot do anything if we continually get assigned "bad inputs", that is, input which cause our program to run at its worst-case complexity
With randomised algorithm, we randomise any input we get, so we know the distribution of our input data
- we are changing the input data
- this can be a bad thing to do sometimes

Probabilistic Analysis vs Randomised Algorithms

9.2 - Randomised Algorithms

Deterministic algorithm

"Here is one input, what is the average running time?"

/\_/\ ???
(='_' )
(, (") (")

Probabilistic algorithm

"Here is one input, what is the expected running time?"

                           (\____/)   i gots you

( ͡ ͡° ͜ ʖ ͡ ͡°)
\╭☞ \╭☞

TLDR version

Why Randomised Algorithms?

9.2 - Randomised Algorithms

Reasons for using randomised algorithms:
- because we want to avoid "bad inputs" (as mentioned before)
- because the deterministic approach may take too long (probabilistic algorithm)
- because you are doing cryptography or security (nonce)
Reasons for NOT using randomised algorithms:
- because you do not like the distribution of the input data
  - maybe most input data cause your program to run for too long
  - but this can be the characteristic of the data that you shouldn't change

Example - Quicksort

9.2 - Randomised Algorithms

https://en.wikipedia.org/wiki/File:Sorting_quicksort_anim.gif

Example - Quicksort

9.2 - Randomised Algorithms

In quicksort, the main function we call is the partition function
- partition function arranges the array so that anything to the left of the pivot element is smaller than the pivot element, and anything to the right is larger than the pivot element

Example - Quicksort

9.2 - Randomised Algorithms

In quicksort, the main function we call is the partition function
- partition function arranges the array so that anything to the left of the pivot element is smaller than the pivot element, and anything to the right is larger than the pivot element

Example - Quicksort

9.2 - Randomised Algorithms

In quicksort, the main function we call is the partition function
- partition function arranges the array so that anything to the left of the pivot element is smaller than the pivot element, and anything to the right is larger than the pivot element

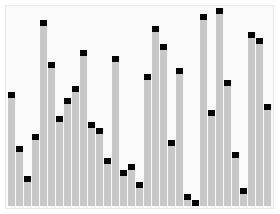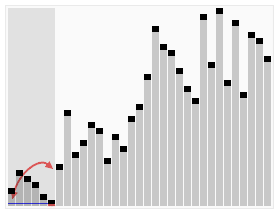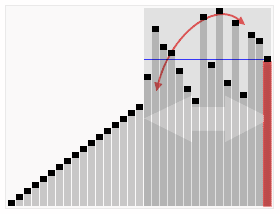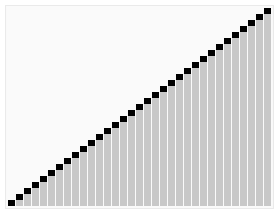
Example - Quicksort

9.2 - Randomised Algorithms

On average, quicksort takes \(O(n\log n)\) operations where \(n\) is the size of the array (you have to call partition \(n\) times)
The recursive relation is
- \(T(n) = 2T(n/2) + O(n) = O(n \log n)\)

\(n\)

\(\frac{n}{2}\)

\(\frac{n}{4}\)

\(\frac{n}{2}\)

\(\frac{n}{4}\)

Example - Quicksort

9.2 - Randomised Algorithms

However, in the worst case, the pivot that you choose is larger (or smaller) than every other element in the array, so the subproblem has \((n-1)\) elements left to process

Example - Quicksort

9.2 - Randomised Algorithms

The recursive relation is now
- \(T(n) = T(n-1) + n\)
- this is \(O(n^2)\)
In reality, this is very rare (we will discuss this in the workshop)

\(n\)

\(n-1\)

\(n-2\)

\(n-3\)

Example - Quicksort

9.2 - Randomised Algorithms

In the randomised version of quicksort, we do not use the first element of the array as the pivot
Instead, we pick the random element in the array as the pivot, thus removing the possibility of having to work with a series of "bad inputs"
- you can see the proof in CLRS 7.4 (pages 182-183), but this is not examinable
Is it worth doing so?
- worst-case complexity is \(O(n^2)\)
- average-case is \(O(n\log n)\)
- randomising the input is \(O(n)\), so yes, it is worth it

Example - Quicksort

9.2 - Randomised Algorithms

Is this what you do?
No, there's a better way, no need to randomise the whole array, simply pick a random element in the array as the pivot!
- on average, even if the array is sorted, you should pick something around the middle of the array, and so your recursion tree should be mostly balanced
- it's pretty much \(O(1)\) (you just generate a random number)

Randomised Algorithms vs Probabilistic Algorithms

9.2 - Randomised Algorithms

There is another type of probabilistic algorithms, and in fact, this is probably the one you have seen before
- randomised algorithms: we modify a deterministic algorithm by randomising the input
- probabilistic algorithms: algorithms where randomness is part of the algorithm
  - we mentioned before that you may want to do this because deterministic algorithm takes too long
  - example: primality testing or factorisation
In the end, they are both randomised or probabilistic, and I don't want to worry too much about the definitions

Example - Matrix Multiplication Verification

9.2 - Randomised Algorithms

Problem: given three \(n \times n\) matrix, \(A\), \(B\), and \(C\), verify whether or not \(AB = C\)
The naive method for solving this is \(O(n^3)\) (i.e. do the matrix multiplication)

\[\begin{bmatrix} 5 & 5 & 3 \\ 7 & 1 & 3 \\ 4 & 1 & 5 \end{bmatrix}\]

\[\begin{bmatrix} 9 & 3 & 2 \\ 4 & 2 & 1 \\ 7 & 7 & 7 \end{bmatrix}\]

\[\begin{bmatrix} 86 & 46 & 36 \\ 88 & 44 & 36 \\ 75 & 49 & 44\end{bmatrix}\]

?=?

Example - Matrix Multiplication Verification

9.2 - Randomised Algorithms

A probabilistic approach:
- Choose a random vector \(x\), then multiply both sides by \(x\)

\[\begin{bmatrix} 5 & 5 & 3 \\ 7 & 1 & 3 \\ 4 & 1 & 5 \end{bmatrix}\]

\[\begin{bmatrix} 1 \\ 1 \\ 1 \end{bmatrix}\]

\[\begin{bmatrix} 86 & 46 & 36 \\ 88 & 44 & 36 \\ 75 & 49 & 44\end{bmatrix}\]

\[\begin{bmatrix} 9 & 3 & 2 \\ 4 & 2 & 1 \\ 7 & 7 & 7 \end{bmatrix}\]

\[\begin{bmatrix} 1 \\ 1 \\ 1 \end{bmatrix}\]

\[\begin{bmatrix} 168 \\ 168 \\ 168 \end{bmatrix}\]

Example - Matrix Multiplication Verification

9.2 - Randomised Algorithms

\[\begin{bmatrix} 5 & 5 & 3 \\ 7 & 1 & 3 \\ 4 & 1 & 5 \end{bmatrix}\]

\[\begin{bmatrix} 1 \\ 1 \\ 1 \end{bmatrix}\]

\[\begin{bmatrix} 86 & 46 & 36 \\ 88 & 44 & 36 \\ 75 & 49 & 44\end{bmatrix}\]

\[\begin{bmatrix} 9 & 3 & 2 \\ 4 & 2 & 1 \\ 7 & 7 & 7 \end{bmatrix}\]

\[\begin{bmatrix} 1 \\ 1 \\ 1 \end{bmatrix}\]

\[\begin{bmatrix} 168 \\ 168 \\ 168 \end{bmatrix}\]

can be done in \(O(n^2)\)

can this be done in \(O(n^2)\)

Example - Matrix Multiplication Verification

9.2 - Randomised Algorithms

\[\begin{bmatrix} 5 & 5 & 3 \\ 7 & 1 & 3 \\ 4 & 1 & 5 \end{bmatrix}\]

\[\begin{bmatrix} 1 \\ 1 \\ 1 \end{bmatrix}\]

\[\begin{bmatrix} 86 & 46 & 36 \\ 88 & 44 & 36 \\ 75 & 49 & 44\end{bmatrix}\]

\[\begin{bmatrix} 9 & 3 & 2 \\ 4 & 2 & 1 \\ 7 & 7 & 7 \end{bmatrix}\]

\[\begin{bmatrix} 1 \\ 1 \\ 1 \end{bmatrix}\]

\[\begin{bmatrix} 168 \\ 168 \\ 168 \end{bmatrix}\]

can be done in \(O(n^2)\)

can this be done in \(O(n^2)\)

yes!

\[\begin{bmatrix} 14 \\ 7 \\ 21 \end{bmatrix}\]

\[\begin{bmatrix} 5 & 5 & 3 \\ 7 & 1 & 3 \\ 4 & 1 & 5 \end{bmatrix}\]

\[\begin{bmatrix} 168 \\ 168 \\ 168 \end{bmatrix}\]

Example - Matrix Multiplication Verification

9.2 - Randomised Algorithms

If \(AB \ne C\), then if we choose a random vector \(x\), the probability that \(ABx = Cx\) is small
However, even if the probability is not that small, we can use a technique known as probability amplification:
- suppose that \(AB \ne C\)
- suppose that there is a 50% chance that if \(AB \ne C\), we still have \(ABx = Cx\)
- pick another random vector \(x^\prime\) and run the process again, if \(ABx_1 = Cx_1\), then the probability that \(AB = C\) is now 25%
- every time you pick another random vector, you halve the chance of being wrong, so after \(k\) trials, the probability is \((1/2)^k\), which is quite small
  - \((1/2)^{10} = 0.0009765625\)

Example - Matrix Multiplication Verification

9.2 - Randomised Algorithms

If at any point \(ABx_k \ne Cx_k\), then you know for sure that \(AB \ne C\)
The cost of this approach can still be \(O(n^2)\) assuming the number of trials is not too big
- this is a common technique in cryptography, e.g. with primality testing and factorisation
- the probability of being wrong is small, so we do several trials

Example - Fermat's Primality Testing

9.2 - Randomised Algorithms

If we want to know if a number is prime for sure, we have to do trial division, many many many times
- however, with the above formula, we can simply do one exponetiation
- pick a random \(a\), compute \(a^{N-1} \pmod N\) where \(N\) is the number we want to test, and if it is equal to \(1\), there is a chance that \(N\) is prime
- do this multiple times with different values of \(a\)
- it doesn't always work, there are things called the Carmichael numbers that will mess this up, but it has a good probability of working

\(a^{p-1} \equiv 1 \pmod p\) for primes \(p\)

Monte Carlo vs Las Vegas Algorithms

9.2 - Randomised Algorithms

There are two major classes for probabilistic algorithms
- Las Vegas algorithms
  - always give correct answers, but may not finish
- Monte Carlo algorithms
  - always give an answer (always finishes), but may give an incorrect answer

Monte Carlo vs Las Vegas Algorithms

9.2 - Randomised Algorithms

Las Vegas Search Algorithm

Random rgen = new Random();
int x = 0;

while (x  != target){
  x = a[rgen.nextInt(a.length)];
}

Monte Carlo Search Algorithm

Random rgen = new Random();
int x = 0;

while (x  != target && count < max){
  count++;
  x = a[rgen.nextInt(a.length)];
}

Monte Carlo vs Las Vegas Algorithms

9.2 - Randomised Algorithms

Examples:
- Bogosort
  - a.k.a permutation sort, slowsort, (censored)-sort, shotgun sort, monkey sort, stupid sort)
  - is it Las Vegas or Monte Carlo?
    - depends on how you implement it
    - if you let it run forever until it returns the correct answer, then it is a Las Vegas algorithm
    - if you stop it after some time, then it is a (very bad) Monte Carlo algorithm

Monte Carlo vs Las Vegas Algorithms

9.2 - Randomised Algorithms

Generally you can convert a Las Vegas algorithm into a Monte Carlo one by putting a time limit
- e.g. after a certain number of operation, just give me whatever you found, no need to check if it's correct or not
Conversely, you can convert a Monte Carlo algorithm to a Las Vegas algorithm by adding a correctness check and removing the time limit
Often it is just how you choose to implement the algorithm

Monte Carlo vs Las Vegas Algorithms

9.2 - Randomised Algorithms

Randomised quicksort:
- Monte Carlo or Las Vegas?
Matrix multiplication verification
- Monte Carlo or Las Vegas?
Primality Testing
- Monte Carlo or Las Vegas?

The End

9.2 - Randomised Algorithms

Main takeaways:
- understand the basics of using probabilistic analysis (expected values) to work out the average-case complexity of your code
- understand the difference between probabilistic analysis and probabilistic algorithm (or randomised algorithm)
- understand why you want to use a randomised algorithm
- understand the difference between Monte Carlo and Las Vegas algorithms

COMP3010 - 9.2 - Randomised Algorithms

By Daniel Sutantyo

COMP3010 - 9.2 - Randomised Algorithms

COMP3010: Algorithm Theory and Design

9.2 - Randomised Algorithms

Prelude

Prelude

Prelude

Fisher-Yates Shuffle

Randomising Input

Probabilistic Analysis vs Randomised Algorithms

Probabilistic Analysis vs Randomised Algorithms

Probabilistic Analysis vs Randomised Algorithms

Why Randomised Algorithms?

Example - Quicksort

Example - Quicksort

Example - Quicksort

Example - Quicksort

Example - Quicksort

Example - Quicksort

Example - Quicksort

Example - Quicksort

Example - Quicksort

Randomised Algorithms vs Probabilistic Algorithms

Example - Matrix Multiplication Verification

Example - Matrix Multiplication Verification

Example - Matrix Multiplication Verification

Example - Matrix Multiplication Verification

Example - Matrix Multiplication Verification

Example - Matrix Multiplication Verification

Example - Fermat's Primality Testing

Monte Carlo vs Las Vegas Algorithms

Monte Carlo vs Las Vegas Algorithms

Monte Carlo vs Las Vegas Algorithms

Monte Carlo vs Las Vegas Algorithms

Monte Carlo vs Las Vegas Algorithms

The End

COMP3010 - 9.2 - Randomised Algorithms

More from Daniel Sutantyo