Multilevel Modeling, Part 2

PSY 716

• Assessing the assumptions of multilevel models
  • ​Why we care
  • Graphical evaluation
  • What to do when assumptions are violated
• Centering
• Longitudinal applications of multilevel models

Plan for this section

Assumptions

• Some are very similar to linear regression
  • Assumption 1: Normality of residuals
  • Assumption 2: Linearity of relationship between predictors and outcome
• Some are a little different with multilevel models​
  • ​Assumption 3: Homoscedasticity of residuals across groups

Assumptions

• We assume that residuals are normally distributed. 
• Note that this does not mean that the variables themselves are normally distributed!
• How serious is this assumption?
  • Appears to be less important at larger sample sizes.
  • Very closely related to our other assumptions.

Assumption 1

• We assume that the predictors have a linear relationship to the outcome.
• How serious is this assumption?
  • Fairly serious, actually.
  • Misspecifying the shape of the relationship gives biased coefficients and can lead to incorrect inferences.
• "Linear in the parameters" vs. nonlinear 

Assumption 2

• We assume two things about the residual variance:
  • A single residual variance \(\sigma^2\) applies to all groups (i.e., homoscedasticity)
  • There are no residual covariances between groups
    • e.g., math scores in School 1 and School 2 are unrelated to one another.
• How serious is this assumption?
  • Potentially serious.
  • Misspecifying the shape of the relationship gives biased coefficients and can lead to incorrect inferences.

Assumption 3

• These assumptions can actually be relaxed
• Homoscedasticity
  • Single variance \(\sigma^2\) can be extended to group-specific variance \(\sigma_j^2\)
• No residual covariances
  • We typically cannot (and do not want to) freely model all residual covariances
  • But we can test specific error structures - e.g., allowing a single parameter to summarize the covariance between schools (compound symmetry)
  • Won't go over this today, but this presentation is great

Assumption 3

• For homoscedasticity, we can test whether allowing group-specific variances improves model fit using likelihood ratio tests.
• For everything else, we have a lot of graphical tools at our disposal
• Lots of judgment calls to make, just like in linear regression

How do we test these?

Centering

• Let's say it right off the bat: centering is confusing.
  • And there are lots of different opinions on best practices!
• It can allow us to do two important things:
  • Disaggregate between-groups and within-group variance
  • Put intercepts on an interpretable scale

Centering predictors

• One option: grand mean centering​
• Example from before: Percent FRL across schools

• We denote the grand-mean centered percent FRL

Centering level-2 predictors

\(PctFRL_j = \) percent FRL in school \(j\)

\(\overline{PctFRL} = \frac{\sum_{j=1}^J{PctFRL_j}}{J}\)

\(= \) the unweighted mean of percent FRL across all schools

\(PctFRL_j - \overline{PctFRL}\)

Level 2

Level 1

Returning to the intercepts-as-outcomes model

By centering the predictor, we will change the interpretation of the intercept. Currently \(\gamma_{00}\) is interpreted as the predicted value for a school where 0% of kids are eligible for free or reduced lunch.

Level 2

Level 1

Returning to the intercepts-as-outcomes model

Now \(\gamma_{00}\) is interpreted as the predicted value for a school with a(n unweighted) average number of kids eligible for free or reduced lunch.

Centering Level-1 predictors

• Two options: grand mean centering​ or group mean centering
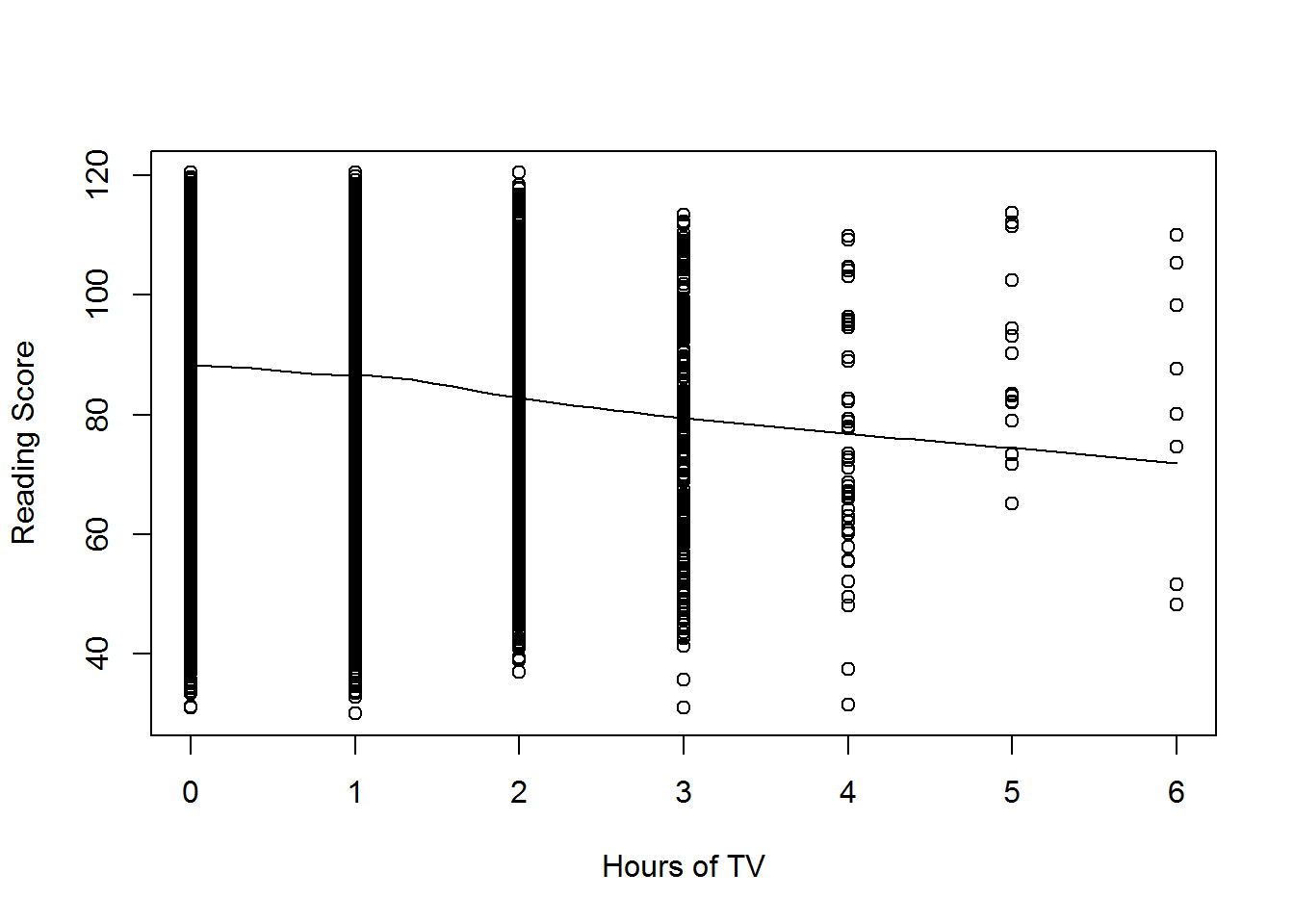
• Example from before: Hours of TV watched
  • \(HoursTV_{ij} = \) Number of hours of TV child \(i\), attending school \(j\), watches

Group mean

Group mean-centered

Grand mean

Grand mean-centered at Level 1

The distance between subject \(i\) and the whole sample average

The distance between subject \(i\) and the average for their school

Level 2

Level 1

Returning to the intercepts-as-outcomes model

Now \(\beta_{0j}\) is interpreted as the predicted value of math score for a child who watches the average number of hours of TV, conditional on percent free or reduced lunch.

Group mean

Group mean-centered

Grand mean

Grand mean-centered at Level 1

The distance between subject \(i\) and the whole sample average

The distance between subject \(i\) and the average for their school

Level 1

The average number of hours of TV watched by students in school \(j\)

Level 2

Group mean

Level 2

Level 1

Returning to the intercepts-as-outcomes model

Now \(\beta_{0j}\) is interpreted as the predicted value of math score for a child who watches the average amount of TV among children at their school.

...but it is a confounded estimate, in the sense that it also potentially contains between-school differences.

Level 2

Level 1

Returning to the intercepts-as-outcomes model

Now \(\beta_{0j}\) is interpreted as the predicted value of math score for a child who watches the average amount of TV among children at their school, \(\beta_{1j}\) conveys the effect of a student's difference from this average. Similarly, \(\gamma_{02}\) conveys the effect of a school's average TV-watching.

Special cases

The paired samples t-test examines the difference between paired observations:

$$t = \frac{\bar{d}}{\frac{s_d}{\sqrt{n}}}$$

Where:

• \(d_i = y_{i1} - y_{i0}\) (difference between paired observations)
• \(\bar{d}\) is the mean of differences
• \(s_d\) is the standard deviation of differences
• \(n\) is the number of pairs

Paired-samples t-tests as MLM's

We can reframe this as a multilevel model, with measurements nested within subjects:

Level 1

where:

• \(y_{ij}\) is the outcome for subject \(j\) at measurement \(i\)
• \(G_{ij}\) is the dummy-coded group variable (0 = condition 0, 1 = condition 1)
• \(r_{ij}\) is the measurement-level residual
• \(\gamma_{00}\) is the average outcome in condition 0
• \(\gamma_{10}\) is the average difference between conditions
• \(u_{0j}\) are subject-level random effects

$$\beta_{0j} = \gamma_{00} + u_{0j}$$

$$y_{ij} = \beta_{0j} + \beta_{1j}G_{ij} + r_{ij}$$

Level 2

$$\beta_{1j} = \gamma_{10}$$

• \(\gamma_{10}\) is equivalent to \(\bar{d}\) in the paired t-test
• Testing \(H_0: \gamma_{10} = 0\) is equivalent to the paired t-test
• Critical note: standard paired-samples t-test does NOT include random slope
• The multilevel approach allows for:
  • Missing data
  • Inclusion of covariates
  • More complex variance structures

Interpretation

Repeated measures ANOVA examines differences across multiple conditions within subjects:

$$ F = \frac{MS_{group}}{MS_{error}} = \frac{\frac{SS_{group}}{df_{group}}}{\frac{SS_{error}}{df_{error}}} $$

where:

• \( SS_{group} \) is the sum of squares for group effect
• \( SS_{error} \) is the sum of squares for error
• \( df_{group} = k - 1 \) (\( k \) is the number of conditions)
• \( df_{error} = (N-1)(k-1) \) (N is the number of subjects)

Key assumption: Sphericity (equal variances of differences between all pairs of conditions)

Repeated-measures ANOVA's as MLM's

We can reframe this as a multilevel model with measurements nested within subjects:

$$y_{ij} = \beta_{0j} + \sum_{m=1}^{k-1} \beta_{mj}G_{mij} + r_{ij}$$

$$\beta_{0j} = \gamma_{00} + u_{0j}$$

$$\beta_{mj} = \gamma_{m0}$$

where:

• \( y_{ij} \) is the outcome for subject \( j \) at measurement occasion \( i \)
• \( G_{mij} \) are dummy codes for conditions (reference is condition 0)
• \( r_{ij} \) is the measurement-level residual with variance \( \sigma^2 \)
• \( \gamma_{00} \) is the average outcome in the reference condition
• \( \gamma_{m0} \) represents mean differences between each condition and reference
• \( u_{0j } \) are subject-level random effects with variance \( \tau^2 \)

Level 1

Level 2

• Testing omnibus hypothesis \( (H_0: \gamma_{10} = \gamma_{20} = ... = \gamma_{(k-1)0} = 0) \) is equivalent to repeated measures ANOVA F-test
• The multilevel approach offers several advantages:
  • Handles missing data appropriately
  • Allows inclusion of subject-level and time-varying covariates
  • Can model more complex variance structures beyond sphericity
  • Permits random slopes (allowing treatment effects to vary by subject)
  • Accommodates continuous predictors and more complex designs
  • Can handle unbalanced designs and irregular measurement occasions

Note: The standard RM-ANOVA assumes compound symmetry and sphericity, while multilevel models can relax these assumptions by specifying different variance-covariance structures.

Interpretation

Multilevel models for longitudinal data

• Here, we consider a single person as a "group", in the sense that all time points are nested within a given person. 
• We will use time as a Level-1 predictor.
• The models we're going over can be considered a special case of structural equation models.
• One piece of advice: don't get too hung up on which piece of MLM jargon (e.g., intercepts-as-outcomes, slopes-as-outcomes) each model maps onto.

Longitudinal data

• Nationally representative survey of \(N=6504\) adolescents 
• Each followed up for a maximum of five time points
• Ages at the first time point ranged from 13 to 21.
• Ages at the fifth time point ranged from 35 to 42.
• We are using data from the first four time points.
• Here, we predict drinking score, a composite score of three drinking-related indicators, from adolescence through early adulthood.

Motivating Example: Add Health

Level 2

Level 1

Random-intercept model

Here, \(Age_{ij}\) and \(Drinking_{ij}\) are the age and drinking score, respectively, of subject \(j\) at time \(i\), and  Note that under this formulation, only the intercept can vary by person. 

Level 2

Level 1

Random-slopes model

Now, under this formulation, we can have variation in the slopes by person.

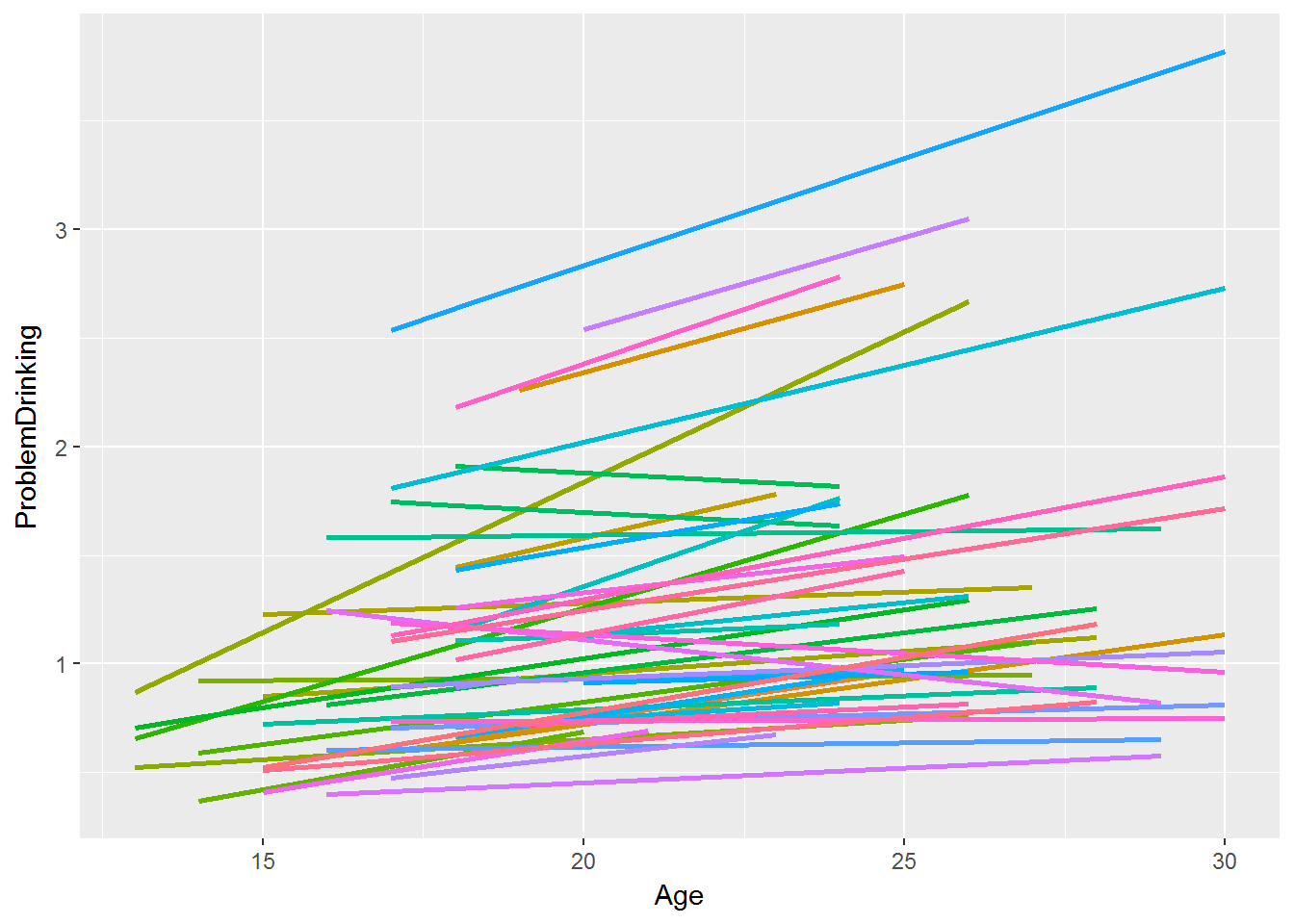
• For linear growth, we can just put age in there, or we can alter it any number of ways:
  • We can subtract out the first time
  • We can rescale it by some multiple (e.g., 10)
    • Sometimes this helps with convergence
• We can also enter a quadratic component of time - i.e., \(age^2\).
  • Or cubic (\(age^3\)), quartic (\(age^4\)), not sure if quintic (\(age^5\)) is a word but let's go with it...
• ​Note that if you enter in a polynomial, you must include all lower-order polynomials.

How does time enter the model?

Level 2

Level 1

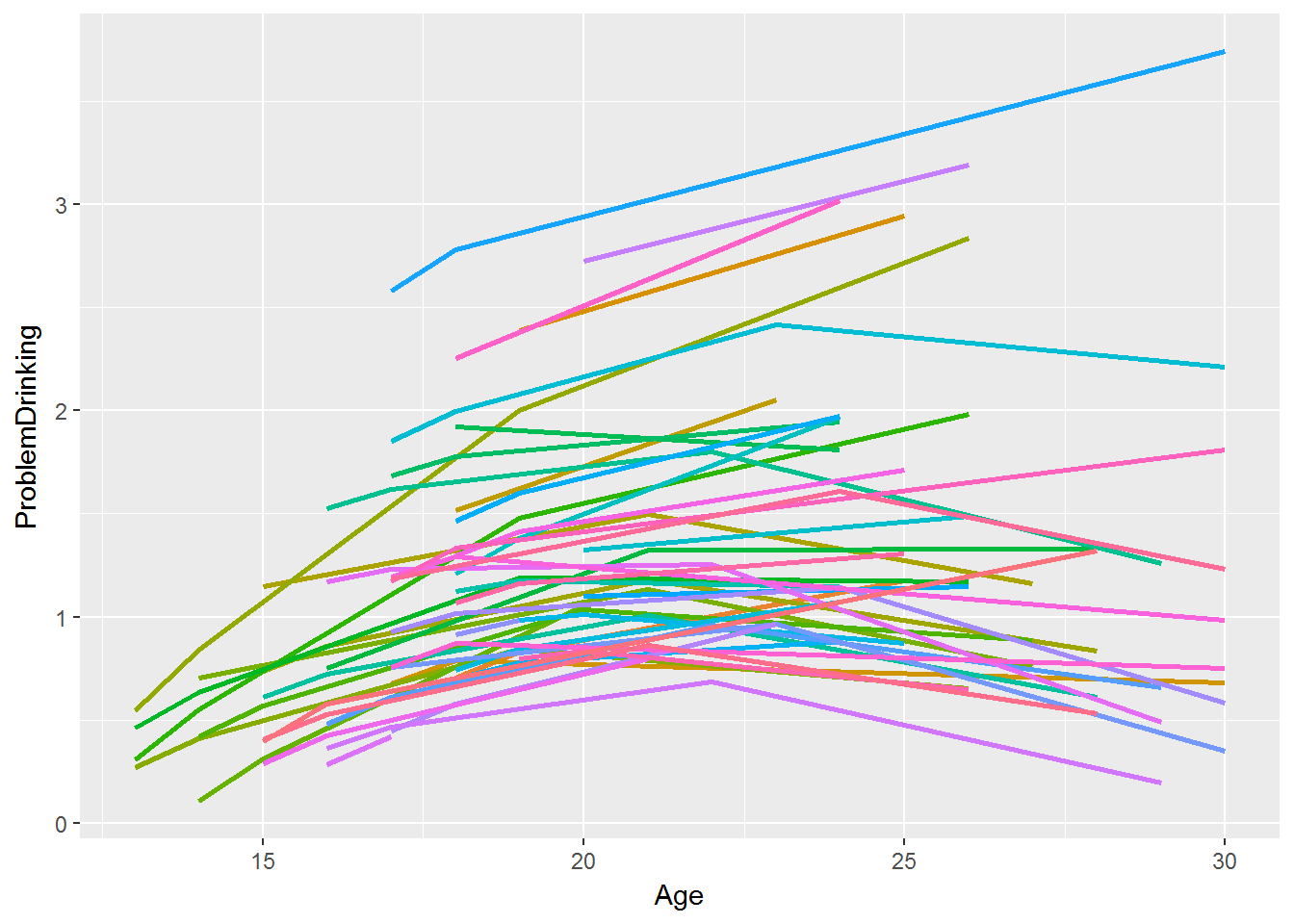
Adding a quadratic component

This can help us to model change that increases and subsequently decreases or levels off. Note that we could include a random effect for that quadratic component too.

• Level 2: We can add person-level predictors by allowing the intercept, slope, or both to vary for different people.
  • Again, this is the same as the intercepts-as-outcomes and slopes-as-outcomes model, but don't worry too much about the terminology.
• Level 1: We can add a time-level predictor, but note that the interpretation of these coefficients can be challenging.
  • If a variable is contemporaneous with the outcome, it can be challenging to make causal statements.

Predictors

Level 2

Level 1

Adding predictors

Now we have the intercept of drinking being allowed to differ between males and females. We could also allow the slopes to differ.

• Note that, if time points are sufficiently close together, independence of errors may not be a reasonable assumption.
  • For instance, if you are doing an EMA
  • Modeling complex error structures may be possible!
• Always fit the unconditional model first to figure out the general shape of change.

A few more things about longitudinal models....

Thank you!

colev@wfu.edu